三段截尾变量小值概率上界的估计
李宗秀,吴 捷
(1.黑龙江财经学院基础部,哈尔滨150025,2.黑龙江科技学院资源与环境工程学院,哈尔滨150027)
小值概率的研究属于小偏差概率,有着较广的适用性.在国外,对概率界的估计研究的历史较长,能一直追溯到Chebyshev,他在给定一、二阶矩的条件下,对概率进行估计,并给出了切比雪夫不等式,概率估计这一问题在切比雪夫不等式这个结论产生之后,发生了质的飞跃.后来Stieltjes解决了如何找到一个φ(x)使得它的各阶矩∫∞0xkdφ(x),k=0,1……,的值分别与给定的mk相等,其中φ(x)是定义在区间[+0,+∞)上有界的单调不减函数.这为研究小偏差概率提供了一个非常有效的方法.Karlin·S和Isii·K分别独立提出使用对偶理论处理矩问题,这为小偏差概率又提供了一种研究此问题的有效工具;Karlin·S改善了密度函数是单峰分布的截尾变量的切比雪夫不等式,使其应用的范围更加宽广.由于经济和金融领域的需求,均值界的估计问题油然而生,尤其是在期权价格的估计中,均值界的估计问题被广泛研究.Karlik Natarajan 和 Zhou Liyi[1]于 2007 年研究了三段线性函数均值的界,给出了任意随机变量的计算结果.在国内,对概率和均值界的研究处于起步阶段,李文博和刘国庆做了大量的研究工作,研究成果较为显著[3].刘国庆,王敏慧[3]研究了二维变量的概率分布的估计.张银龙和刘国庆[4]在给定一、二阶矩的条件下,对随机变量分布函数上下界进行了估计.宋伟平[5]研究了随机变量X∈(-∞,M]的三段截尾线性函数均值的上界,给出了精确的估计.李宗秀,刘国庆[6]研究了随机变量 X∈[a,+∞)三段截尾变量概率分布的上界,并给出使确界可达的分布.本文通过对三段截尾变量小值概率和均值上界的估计,明确了概率和均值变化的界限,使我们更精确地将其应用于破产理论、金融学、风险投资、保险学、化学等领域.
1 主要结果和证明
定理1:设随机变量 C∈[-a,M -a],a≥0,M>0,且 EX=m1,EX2=m2,三段线性函数 H(x)=max(0,x,mx-z),其中 m >1,z>0.当 M >max(m1,z/(m -1))时,有
1)当t≤z/(m-1)时

且

而且当X在取-a,t,和M-a三个值时等式成立,并且具有

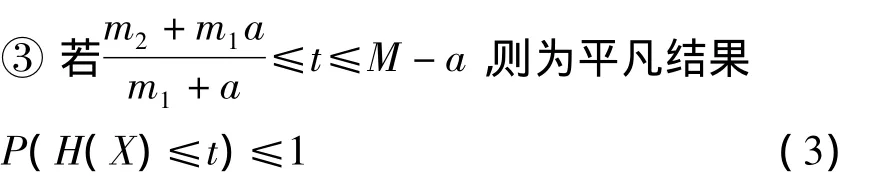

则
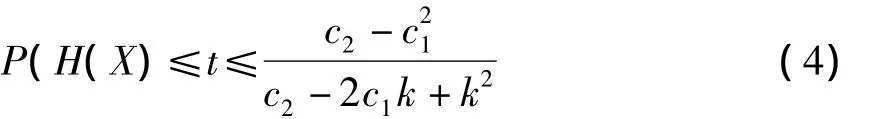

②若

则

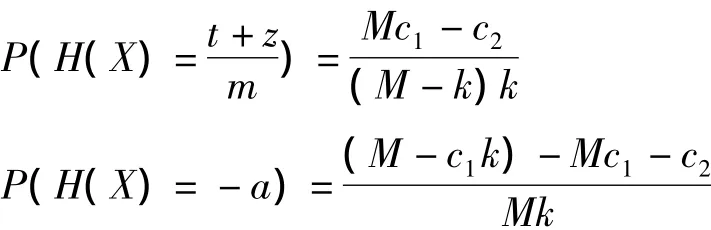

证明 1)当t≤z/(m-1)时,则P(H(X)≤t)=P(X+a≤t+a),记 X+a=Y,t+a=d,Y∈[0,M]则P(H(X)≤t)=P(Y≤d),基本想法是找到一个二次函数 Q(y)=α+βy+γy2,使得示性函数I(Y≤d)≤Q(y),于是
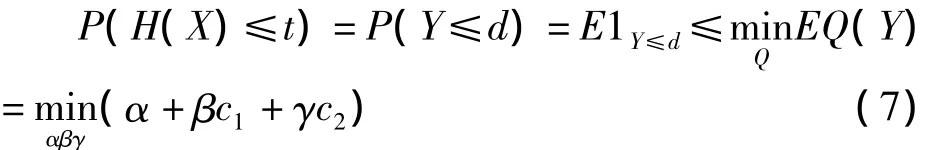

经过计算和比较,当


因此将 c1=m1+a,c2=m2+2am1+a2,Y=X+a,d=t+a代入,当t≤z/(m-1)时,①得证.
②若

由对偶原理可知,必须找到一个非常“好”的二次函数最大程度的逼近示性函数,即找到满足示性函数1Y≤d≤Q(y)的二次函数 Q(y)= α + βy+ γy2,于是
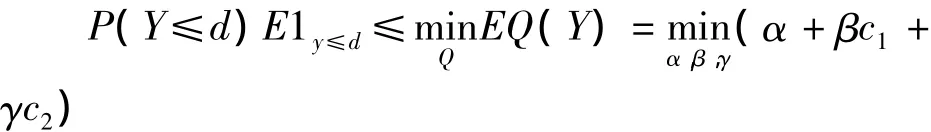
分两种情况讨论:
当γ≥0时,则二次函数Q(y)应满足

解方程组(8)得
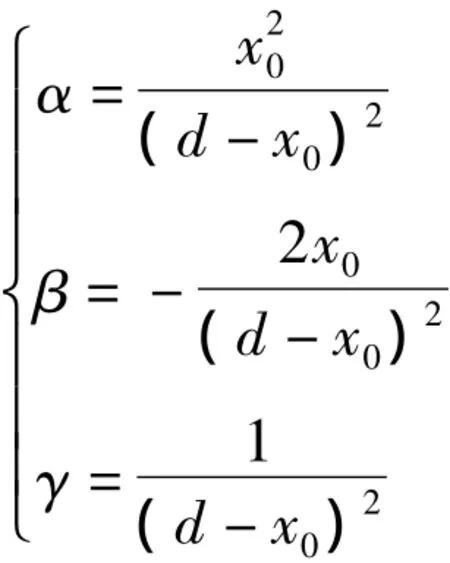
所以

当γ≤0时,则二次函数Q(y)应满足
解方程组(9)得

所以
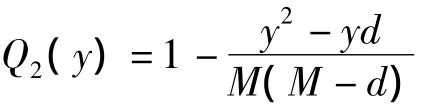
经过计算和比较,当

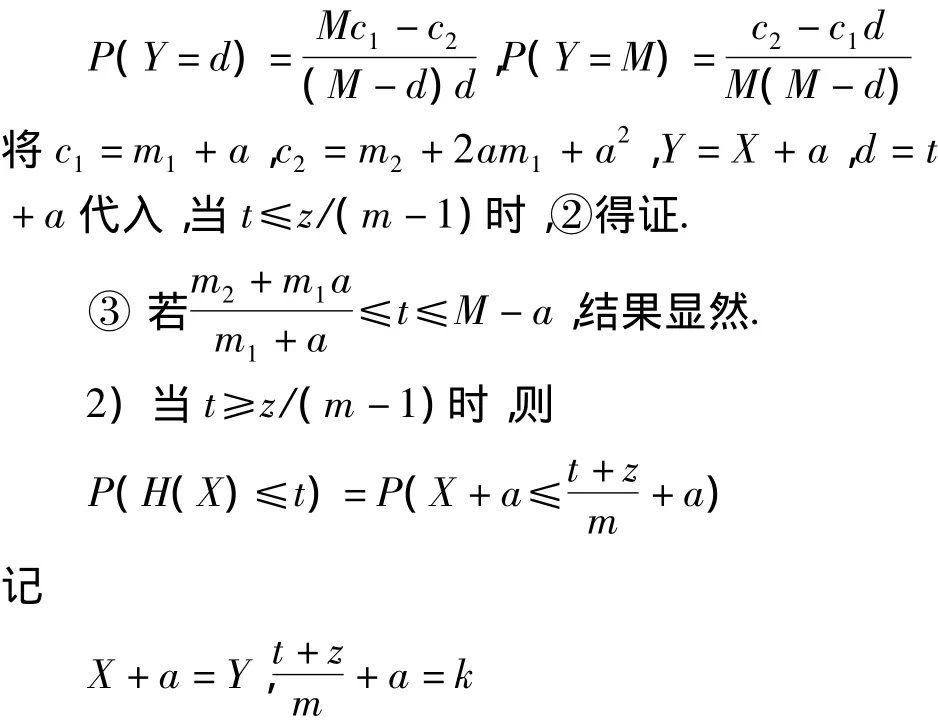
Y∈[0,M],则 P(H(X)≤t)=P(Y≤k)EY=m1+a=c1,EY2=E(X+a)2=m2+2am1+a2=c2证明方法与(1)类似,此不赘述.
2 结语
本文利用对偶的方法,构造了控制函数,分别对三段截尾变量小值概率的上界进行估计.结果深化了对小值概率理论的原有认识,并在金融学、经济学和化学中有着很强的实际应用价值.
[1]NATARAJAN K,ZHOU Y L.A Mean-variance Bound for a Three-piece Linear Function[J].Probability in the Engineering and Informational Sciences,2007,21(4):611 -621.
[2]LIU G Q,LI W V.Semiparametric Bounds of Mean and Variance for Exotic Options[J].Science in China Series A:Mathematics Jul,2009,52(7):1 -14.
[3]LIU G Q,WANG M H.Bounds on Probability and Mean for Truncated Random Variables[J].Journal of Natural Science of Heilongjiang University,2010,2:19-21.
[4]张银龙,刘国庆,王敏慧.两类截尾变量的均值与方差的估计[J].哈尔滨理工大学学报,2010,15(5):74-77.
[5]宋伟平.截尾三段线性函数期望与方差的半参数界[D].哈尔滨:哈尔滨工业大学,2011.
[6]李宗秀,刘国庆.三段截尾变量概率分布的上界[J].高师理科学刊,2011,31(4):11-12.

