导管架式海上风力发电支撑结构振型扩阶方法*
李 炜,王卫英,刘福顺,陈文文,彭春涪,卢洪超
(1.中国水电顾问集团华东勘测设计研究院,浙江 杭州310014;2.青岛理工大学工程质量检测鉴定中心,山东 青岛266033;3.中国海洋大学工程学院,山东 青岛266100)
常规海上风电振动监测时,传感器通常安装在风力发电机附近,并且就目前的安装情况来看,数量非常少,少则1个,多则2~3个。虽然监测信号在一定程度上能够反映风机的运行情况,但对于海上风电支撑结构而言,因传感器距离支撑结构较远,并且支撑结构基本位于水面以下,利用现有的传感器数据无法得知支撑结构的振动情况,包括支撑结构的模态信息,尤其是模态振型。对于海上风电支撑结构而言,水下安装传感器的难度与成本可想而知。
Guyan[1]与Irons[2]最早提出了模型缩阶方法。该方法将质量、刚度矩阵分别对应于主自由度、从自由度进行分解,借助分解后的刚度矩阵计算并获取传递矩阵以达到模型缩阶的目的。虽然该方法是目前最简单的方法,但该方法在很大程度上依赖于主自由度的数量与类型。更重要的是该方法只能在低阶动力特性上具有较好的精度,而对于高阶模态误差较大。为此,许多学者试图进一步提高Guyan方法的精度。Kidder[3]、Miller[4]在一定程度上考虑了惯性力项的影响。Papadopoulos和Garcia[5]提出了2个策略以提高缩减模型的精度。但是,这些改进只有在主自由度选取非常合适的时候才成立。O’Callahan亦在静态缩阶法的基础上进行了改进,提出了改进的缩阶系统(Improved Reduced System)[6]。该方法实际上是通过加入假设的静荷载作为惯性项,在由静态缩阶法得到的转换矩阵中加入了1个修正项。系统等效缩阶扩展(SEREP)方法[7],利用计算的特征向量构造主自由度与从自由度之间的传递矩阵。同静态缩阶方法类似,特征向量也分解为与主自由度和从自由度相对应的两部分,当主自由度数目大于振型阶数时,SEREP的传递矩阵可应用伪逆技术计算获得。值得注意的是,SEREP是1种精确的模型缩阶技术。也就是说,在主自由度测试信息精确的前提下,可获得结构的所有自由度的振型信息。但是,如果实测模态与有限元模态的相关性欠佳,SEREP方法将无法应用。罚函数法[8]借助权重变量作为实测模态的相对可信判别指标,通过使模态应变能最小实现模态扩阶。最近,Chen[9]提出了1种可以考虑有限元模型误差并且允许实测数据具有一定程度测试误差的振型扩阶新方法。该方法利用了质量归一化条件将实测振型表述为各有限元振型的线性组合。
上述方法是通过求解传递矩阵实现模态振型扩阶或模型缩阶的。Liu[10]提出了1种考虑模型误差的振型直接扩阶方法。该方法通过一系列模型修正系数以考虑模型误差,借助振型修正系数实现未测试自由度的估算。但文中算例未讨论三维结构的振型扩阶问题。本文将引入一复合向量,通过对其未测试自由度的振型值进行修正而实现模态振型的直接扩阶,无需求解传递矩阵。文中采用三桩导管架式海上风力发电支撑结构验证提出方法的正确性以及在低阶模态振型扩阶上的优越性。
1 传统方法
Guyan最早提出了模型缩阶方法。该方法的推导过程起始于无阻尼体系的振动方程,即

式中:f为施加于系统的外力矩阵;M、K分别为系统的质量、刚度矩阵。
首先将体系的自由度分解为主自由度和从自由度,然后状态向量x,外力矩阵f以及质量矩阵M ,刚度矩阵K均分解为与主自由度和从自由度相对应的形式,并且在从自由度上无外力,则式(1)可写为

其中:下标m与s分别表示主自由度和从自由度。忽略式(2)中惯性力项,可得以下2个方程
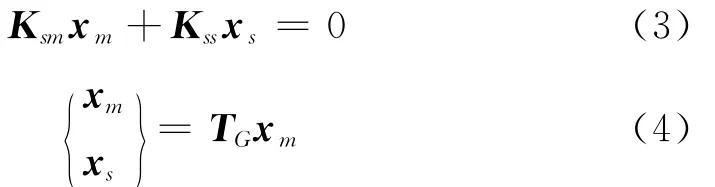
该方法因其原理相对简单,现已成为最常用的模型缩阶方法之一。
Paz[15]对静态缩阶法进行了改进,引入了惯性项。他采用了迭代方法来节省结构特征计算时花费的机时。式(3)进行了改进,加入了初始设定的ω0的惯性项。可以得到

式中
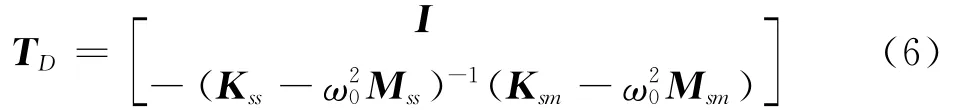
TD为动力缩阶法的转换矩阵。注意到当ω0为0时,这种方法与静态缩阶法是相同的。
SEREP方法利用计算的特征向量构造主自由度与从自由度之间的传递矩阵。同静态缩阶方法类似,特征向量也分解为与主自由度和从自由度相对应的两部分Φm、Φs,并且SEREP的传递矩阵TS定义为

当主自由度数目大于振型阶数时,SEREP的传递矩阵TS可应用伪逆技术计算获得:
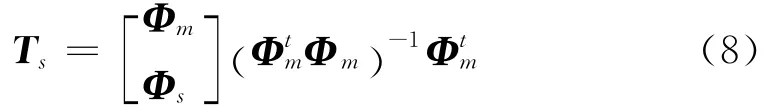
值得注意的是,SEREP是1种精确的模型缩阶技术。也就是说,在主自由度测试信息精确的前提下,可获得结构的所有自由度的振型信息。
2 模态振型的直接扩阶方法
对于第j阶模态,定义一复合向量Φ′j,该向量由对应于主自由度的实测数值及对应于从自由度的待估算数值组成,即:
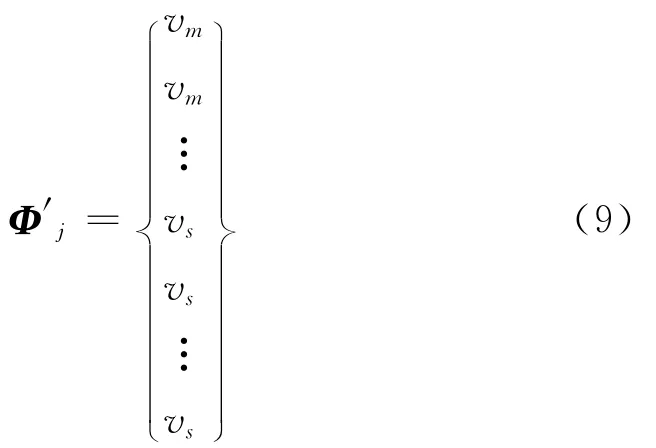
式中下标m与s分别表示主自由度和从自由度。
假定第j阶空间完备的真实振型Φ*j是对复合向量Φ′j在从自由度上修正的结果:
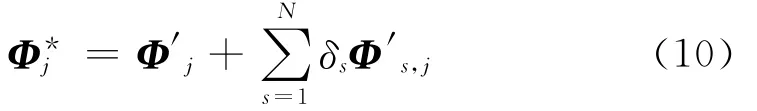
式中:Φ′s,j为在第s个自由度上为非零值而其他自由度上均为零值的与Φ′j同维的向量,N为待修正项(从自由度)的个数,δs为对应的修正系数。
将真实结构的质量、刚度矩阵分别用K*与M*表示,则该结构第j阶特征值与特征向量的关系可表示为:
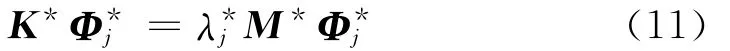
实际上,真实结构的刚度矩阵K*、M*是未知的,并且该矩阵不同于借助有限元手段获取的刚度矩阵K、M。故在提出的方法中,当允许二者存在模型误差时,研究本文方法的可行性,即

假如通过动力测试可获得实测模型的第j阶特征值与特征向量分别为左乘方程(11)的两边,得
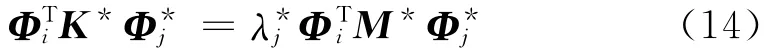
将式(10)、(12)及(13)代入上式,可得
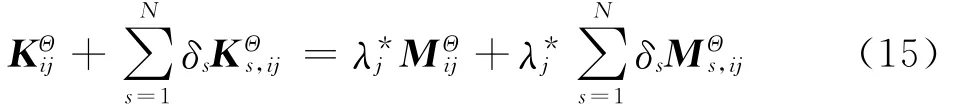
其中
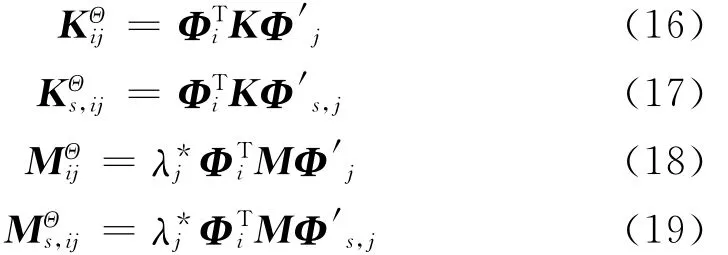
将式(15)整理后,得
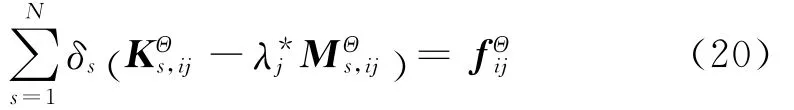
其中
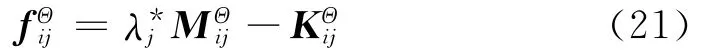
当有Nj阶实测模态,并且从有限元模型中取Ni阶时,依据式(20)可构造Nm=Ni×Nj方程,记
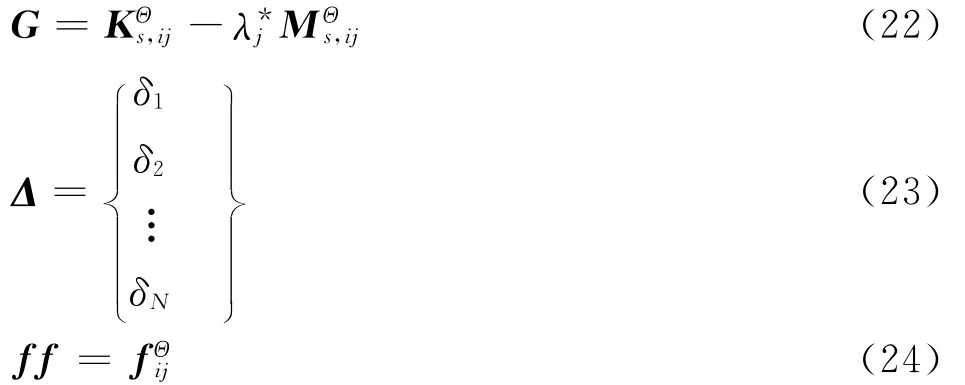
式(20)可进一步写成矩阵的形式,即

理论上,如果G为非奇异的方阵,则式(25)可依据标准的求逆算法得到Δ,即

当G非方阵时,即方程数量与未知数的个数不等时,1个等效的算法就是伪逆技术(Pseudo-Inverse)。若矩阵G*的行数多于列数,则该问题为超静定问题,伪逆算法关于超静定问题的定义为Gelb[16]。
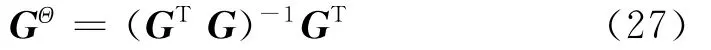
3 三桩导管架式海上风力发电支撑结构
为验证方法的有效性,建立三桩导管架式海上风力发电支撑结构见如图1。该模型共有25个单元组成,其中节点19以下均位于水中。所用材料的杨氏模量为2.1×1011Pa,泊松比为0.3,密度为7 860kg/m3。
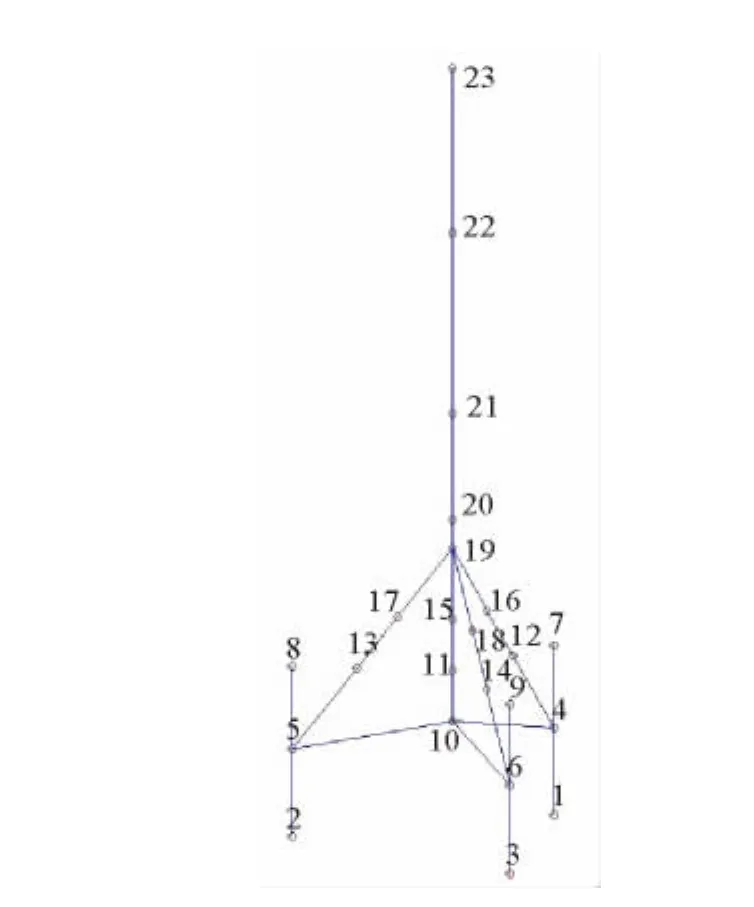
图1 三桩导管架式海上风力发电支撑结构Fig.1 Tripod jacket-type support structure for offshore wind turbine
因有限元建模必然与实际结构之间存在误差,故而实际结构假定单元7、单元14分别具有35%、55%的刚度降低,其他单元刚度均乘上均值为零、方差为0.15的服从高斯分布的刚度变化系数。有限元模型与实际结构的前10阶频率对比见表1。
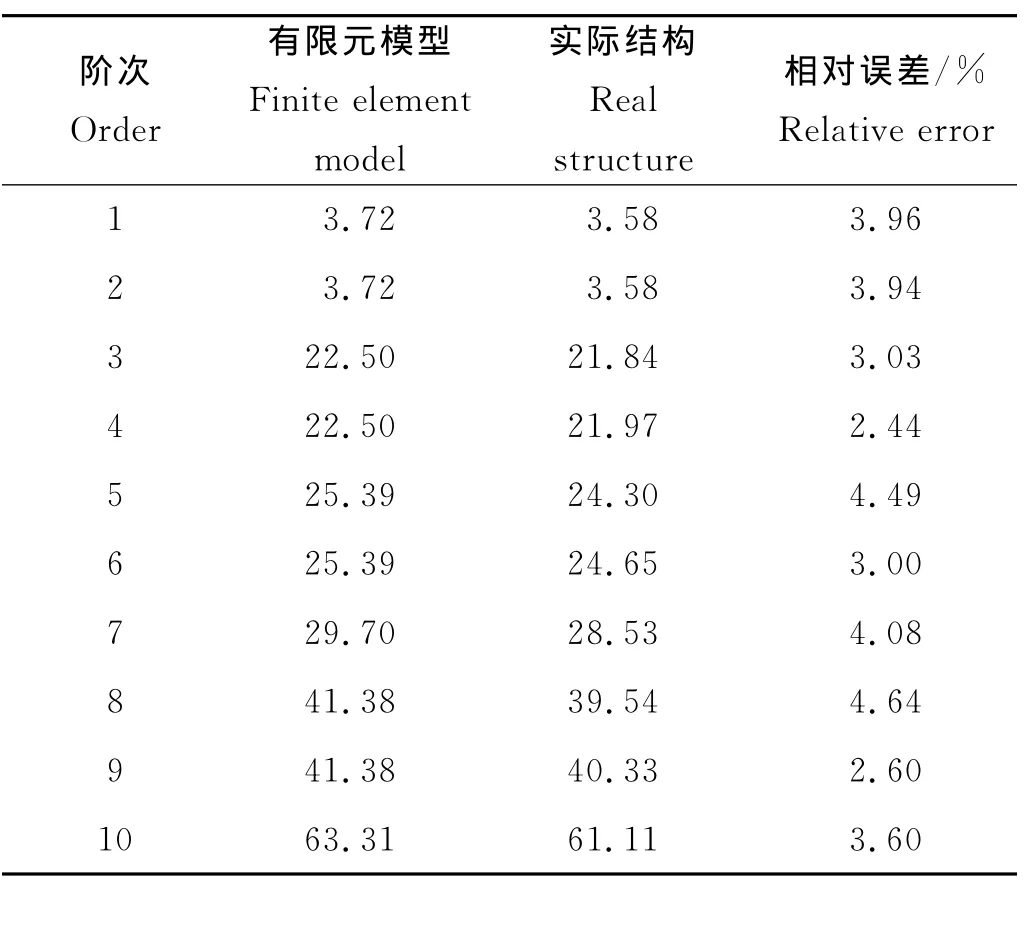
表1 三桩导管架式海上风力发电支撑结构有限元模型与实际结构的前10阶频率Table 1 Comparison of the first ten frequencies between finite element model and actual structure /Hz
首先,检验所提出方法的正确性,即假定K*已知,空间不完备情况考虑为所有节点只有平动自由度可以测得,即从自由度数目为60。从有限元模型中取所有阶次模态,图2为实测结构第10阶振型真实值与应用本文方法的估算值对比图。从图中可以看出,如果K*已知,所发展方法可对海上风电支撑结构振型中未测试位置给出准确的估算。
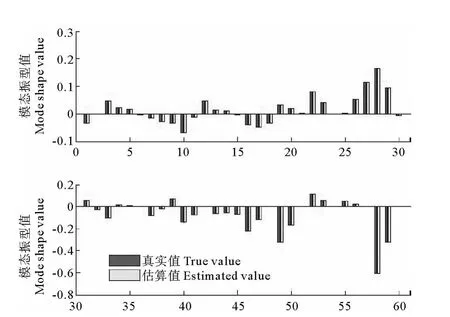
图2 实测结构刚度已知时第10阶振型估算对比图Fig.2 Comparison of the 10th order male shape whenstiffness of real structure is assumeci be known
当然,对于实际海上风电结构,其刚度矩阵K*无法准确得知。作为近似手段,取K*=K,采用与获得图2一致的计算条件可获得当K*=K时实测结构第10阶振型真实值与应用本文方法的估算值对比图,见图3。图3表明,当忽略有限元模型与实际结构的刚度建模误差时,本方法可以得到较高的振型扩阶精度。
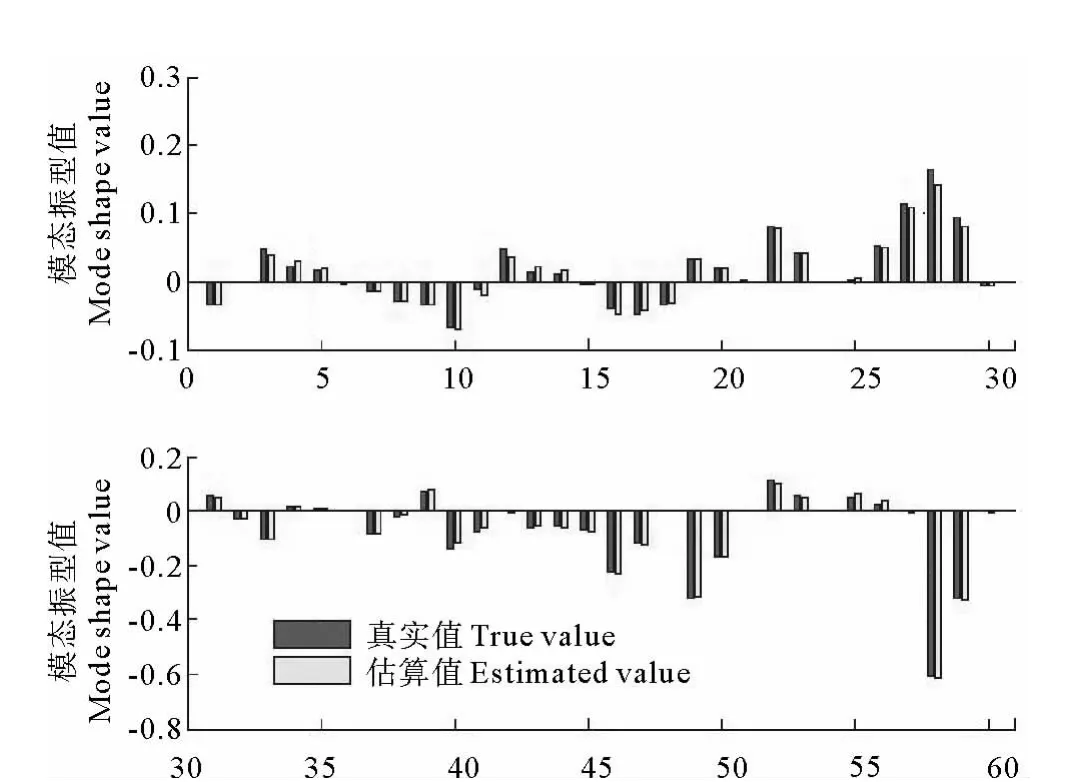
图3 当K*=K时第10阶振型估算对比图Fig.3 Comparison of the 10th order mode shape when K* =K
实际安装传感器时,水深越深,安装难度越大,成本越高,故而假定图1中只有15~23节点的平动自由度可以测得,并且假定实际结构刚度未知而近似取K*=K,得到应用本文方法及Guyan方法获得的前10阶振型与实际结构前10阶振型MAC值(见表2)。计算结果表明,利用传统的Guyan方法虽然在低阶模态上具有较好的精度,但是该技术将损失高阶模态的扩阶精度,如第8、9阶模态 MAC值仅为0.757 3、0.763 3,而本文的方法依然可以保持较好的精度。
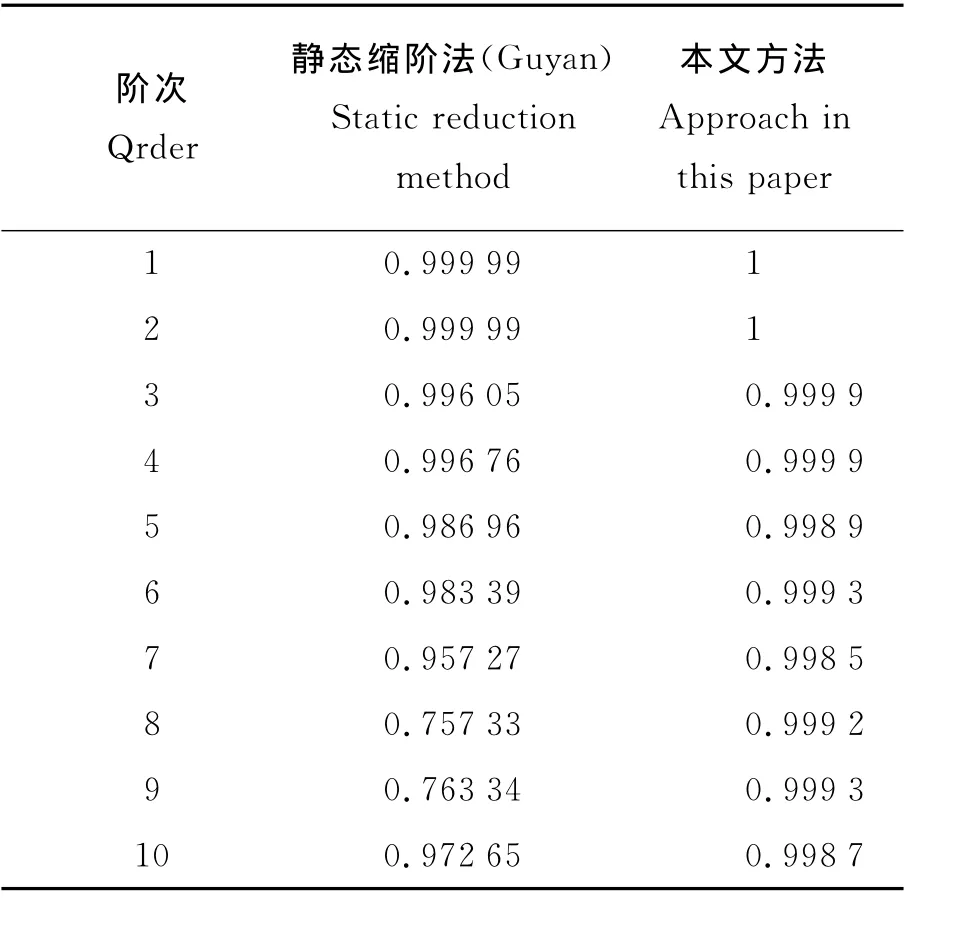
表2 采用本文方法与Guyan方法分别获得的前10阶振型与实际结构前10阶振型MAC值Table 2 MAC values of the first ten mode shapes using the approach and Guyan method /Hz
4 结语
合理有效的实测振型的空间不完备处理技术是模型修正与损伤检测领域中的难题之一,尤其对于绝大部分支撑结构位于水中的海上风力发电结构而言,用数量最少的传感器放在最易于安装的位置上以获得结构的模态振型具有更为重要的意义。本文的方法在一定程度上可以忽略有限元模型与实际结构在刚度特性上的建模误差,通过实测数据直接估算未测试自由度的对应振型值,整个过程无需迭代求解,计算效率较高。三桩导管架式海上风电支撑结构的数值计算结果表明,在传感器数量、位置受到限制时,仅在风电支撑结构的浅水部分节点处布置少数传感器即可比较精确的获得其空间完备模态振型,具有良好的工程应用前景。
[1] Guyan R.Reduction of stiffness and mass matrices[J].AIAA Journal,1965,3(2):380.
[2] Irons B.Structural eigenvalue problems:Elimination of unwanted variables[J].AIAA Journal,1965,3(5):961-962.
[3] Kidder R L.Reduction of structural frequency equations[J].AIAA Journal,1973,11(6):892.
[4] Miller C A.Dynamic reduction of structural models[J].Journal of the Structural Division,1980,106(10):2097-2108.
[5] Michael P,Ephrahim G.Improvement in model reduction schemes using the system equivalent reduction expansion process[J].AIAA Journal,1996,34(10):2217-2219.
[6] O’Callahan J C.A procedure for an improved reduced system(IRS),Seventh International Modal Analysis Conference[C].Las Vegas:Nevada,1989.
[7] Levine-West M,Milman M,Kissil A.Mode shape expansion techniques for prediction:experimental evaluation[J].AIAA Journal,1996,34(4):821-829.
[8] Tikhonov A N,Arsenin V Y.Solutions of Ill-Posed Problems[M].NewYork:Wiley,1977.
[9] Chen H P.Mode shape expansion using perturbed force approach[J].Journal of Sound and Vibration,2010,329:1177-1190.
[10] Liu F S.Direct mode-shape expansion of a spatially incomplete measured mode by a hybrid-vector modification[J].Journal of Sound and Vibration,2011,330:4633-4645

