超混沌Lü系统的同步控制

潘 红

(山西工程职业技术学院基础部，山西太原030002)

1 引言

混沌控制及其应用现已成为非线性科学中的前沿热门课题之一，混沌同步则是混沌控制领域中非常重要的一部分.自从 Pecora和Carmn首次发现现了混沌同步后，人们对混沌同步的做了很多深入的研究.这些研究成果为混沌控制在实际生活的应用提供了重要的理论基础。

超混沌系统是具有两个以上的正的李雅普诺夫指数的混沌系统，它的动力学行为比一般的混沌系统更加复杂，所以在信号加密中应用超混沌系统加密的信号很难被破译，具有很高的安全性。因此，为了使超混沌同步控制在实际中的应用更加的广泛，那么对超混沌系统同步控制的深入的研究就更为重要。在本文中给出了设计超混沌同步控制的一种新方法，然后用超混沌Lü系统理论证明了这个方法的可行性，并用数值仿真说明其正确性和有效性，为超混沌同步控制研究提供有力理论依据。

2 超混沌Lü系统

超混沌Lü系统数学模型为:

系统参数 a=10，b=5，c=3，d=0.5 时，系统的两个正Lyapunov指数分别为1.0596，0.1285，因此系统处于超混沌状态。对应的超混沌Lü系统吸引子在各平面上的投影如图1所示。

3 超混沌Lü系统同步控制

3.1 超混沌同步控制方法

超混沌系统数学模型

其中x(t)∈Rn，f(·)为n维非线性函数，设y(t)∈Rn，为参考信号，若在(2)式中加控制器:

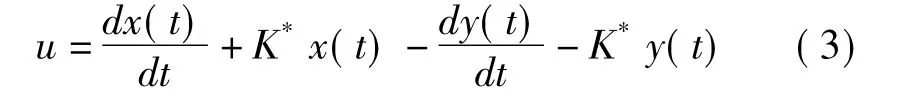
式(3)中K为控制参数，则响应混沌系统为

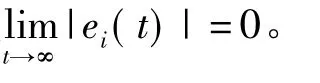
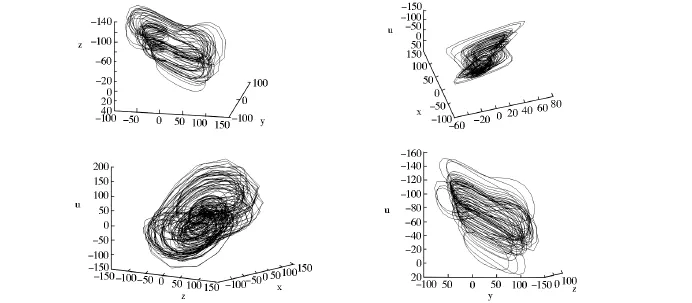
图1 系统的超混沌Lü系统吸引子

3.2 超混沌Lü系统同步控制

(1)式超混沌Lü系统为驱动系统，以(y1，y2，y3，y4)为参考信号，由(3)式所得的控制器如下

得到响应系统为

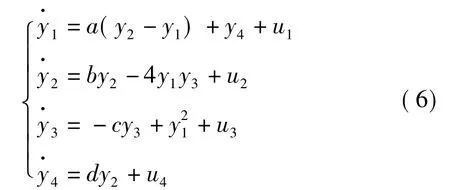
用(6)式和(1)式做差得误差系统:

误差信号为 ei(t)=yi-xi(i=1，2，3，…n)，设 vi(i=1，2，3，4)，如下所示:

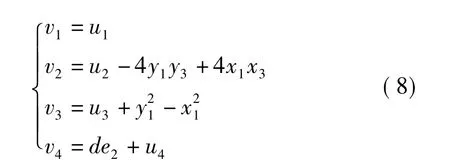
将(8)式代入(7)式，整理得误差系统为

(8)式中的 vi(i=1，2，3，4)是关于误差变量 ei(i=1，2，3，4)函数的控制输入信号，即 vi=Aei，其中A是4×4的实常数矩阵，我们取

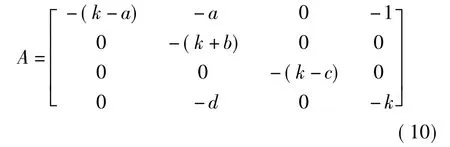
4 数值模拟仿真

应用matlab软件和四阶龙格-库塔法，步长取0.001，K 取值 1000，初值取 x1(0)=0，x2(0)=1，x3(0)=1，x4(0)=-0.3;y1(0)=1.1，y2(0)=1.05，y3(0)=1.4，y4(0)=0;得到超混沌同步系统的同步误差曲线如图2所示。

图2 误差演化曲线图

5 结论

文中提出的超混沌同步控制方法通过理论分析和仿真试验都验证期有效性，说明在初值不同的情况下，超混沌系统是可以达到同步的，并且当控制参数K的越大，超混沌系统同步的所需时间越短。

［1］Pecora L M，，Carroll T L.Synchronization in chaotic system.Phy Rev ett，1990，64;821.

［2］Pecora L M，，Carroll T L.Driving system with chaotia signals.Phy Rev ，1991，A44;2374.

［3］Carroll T L.Pecora L M.Cascading Synchronization chaotic system.Physia，D，1993，67;126.

［4］Maria de Sousa Vieira A J.et al.Synchronization of regular and chaotic system.Phy Rev ，1992，A46;R7359.

［5］He Rong ，Vaidya P G.Analysis and synthesis of synchronous periodic system Phy Rev，1992，A46;7387.

［6］刘扬正.超混沌系统的电路实现［J］.物理学报，2008，(3).