向量在解析几何中的作用

武俊兰

（忻州师范学院，山西 忻州 034000）

1 向量方法在研究几何问题中的作用

从数学或物理学角度讲，向量是指既有方向又有大小的量。与复数相比，向量在数学中发挥的积极效用更为突出。因为复数所对应的点仅能够出现在平面上，而向量所对应的点既能够出现在平面上，又能够出现在空间中。除此之外，向量的相关知识在物理、数学等理科中应用范围较广，并且主要表现为几何形式与代数形式两种重要形式，能够促进物理或数学中诸多主干知识的有效结合。实际上，几何是数学体系的重要组成部分。在大学数学教材中存在着相当一部分几何问题，其中仅凭常规方法只能够解决部分几何问题，还有部分几何问题需要运用向量实现形与数的转化。

工具性是平面向量解决几何问题时的显著特征。实践研究发现，向量方法既能够解决平面几何中的求值和证明问题，又能够解决复数、三角、测量等问题。另外，当运用向量方法解决平面几何问题时，需要将复杂的平面几何问题进一步简化，使其程序化、代数化。

而运用空间向量解决立体几何问题时往往会涉及到位置关系和度量问题，具体内容包括：

（1）位置关系。运用向量方法解决平面几何问题时所涉及到的位置关系包括线面平行、线线垂直、线面垂直及线线平行等。

（2）度量关系。运用向量方法解决平面几何问题时所涉及到的度量问题包括面面所成角问题和线线、线面所成角问题等。

与传统方法相比，运用空间向量解决立体几何问题更容易淡化由“形”到“形”的推理过程，使复杂的立体几何问题趋于程序化。

2 向量方法解决位置、度量问题的直接应用

2.1 两种位置关系

2.1.1 平行

（1）证明两直线平行

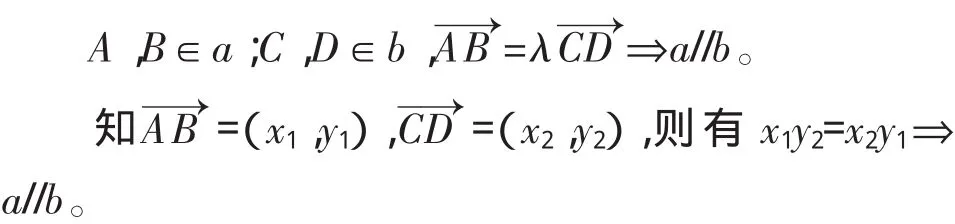
例1 已知直线OA⊥平面α，直线BD⊥平面α，O、B为垂足，求证：OA//BD。

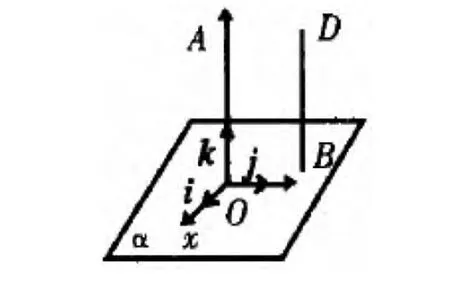
证明：如上图，以点O为原点，以射线OA为z轴，建立空间直角坐标系O-xyz为沿x轴，y轴，z轴的坐标向量，且设

方法思路：在两条直线上分别取不同的两点得到两向量，转化为证明两向量平行。

（2）证明线面平行

方法思路：求面的法向量，在直线找不同两点得一向量，证明这一向量与法向量垂直（即证明数量积为0），则可得线面平行。

（3）面面平行

方法思路：求平面的法向量，转化为证明两法向量平行，则两平面平行。

方法思路：求出其中一平面的法向量，再证该法向量与另一面的不共线的两向量数量积为0（即垂直），则可得两平面平行。

2.1.2 垂直

（1）证明两直线垂直

例2 如图，已知四棱锥P-ABCD的底面为等腰梯形，AB//CD，AC⊥BD，垂足为H，PH是四棱锥的高，E为AD中点。证明：PE⊥BC

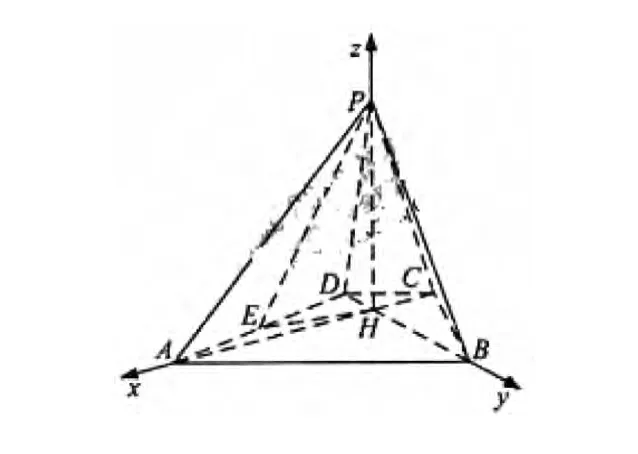
证明：以H 为原点，HA，HB，HP 分别为 x，y，z轴，线段HA的长为单位长，建立空间直角坐标系如图，则 A（1，0，0），B（0，1，）

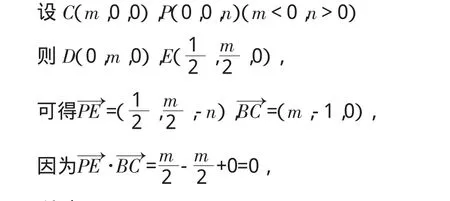
所以PE⊥BC。

（2）证明线面垂直

（3）证明面面垂直

方法思路：找平面的法向量，只需证明两向量数量积为0，则可证明两平面垂直。

2.2 两个度量性质

例3在直平行六面体AC1中，ABCD菱形，∠DAB=60°，AC∩BD=O，AB=AA1.

（1）求证：C1O//平面 AB1D1，

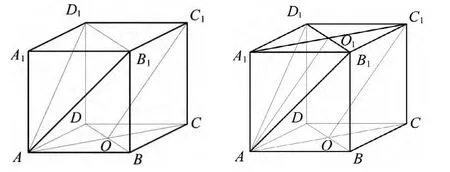
（2）求证：平面 AB1D1⊥平面 ACC1A1，

（3）求直线AC与平面AB1D1所成角的大小.

证明：（1）连接 A1C1交 B1D1于 O1，连结 AO1

在平行四边形AA1C1C中，C1O1//AO，C1O1//AO，

∴四边形AOC1O1为平行四边形

∴C1O//AO1

∵C1O⊄平面 AB1D1，AO1⊂平面AB1D1

∴C1O//平面AB1D1

（2）在直平行六面体AC1中，A1A⊥平面A1B1C1D1

∴A1A⊥B1D1

∵四边形A1B1C1D1为菱形

∴B1D1⊥A1C1

∵A1C1∩AA1=A1，A1C1⊂平面 ACC1A1，AA1⊂平面ACC1A1

∴B1D1⊥平面ACC1A1

∵B1D1⊂平面AB1D1

∴平面AB1D1⊥平面ACC1A1

（3）过C作CH⊥AO1交AO1于H

∵ 平面 AB1D1⊥平面 ACC1A1，平面 AB1D1∩平面ACC1A1=AO1

∴CH⊥平面AB1D1

∴AH为AC在平面AB1D1上的射影

∴∠CAH是AC与平面AB1D1所成的角

设AB=2，在菱形ABCD中，∠DAB=60°

熟悉立体几何中常见问题及处理方法，要求学生敏锐把握所给图形特征，制定合理的解决问题策略。立体几何主要是两种位置关系（平行、垂直），两个度量性质（夹角、距离）。解决问题的方法也有两种：几何方法和向量方法。两种方法各有优缺点，前者难在“找”和“作”的技巧性，后者难在建系和计算上。

3 向量方法解决证明与计算问题有关的综合应用

在进行向量运算时，可以把所有的向量都表示成坐标向量的线性组合，然后进行运算。

在证明两直线垂直时，可把问题转化成这两条直线的方向向量（与直线平行的非零向量）的垂直问题进而转化为两向量数量积为零的问题。

在证明有关长度的等式时，首先将数量转化成向量等式，即用向量的模表示线段的长度，其次运用公式，使问题化为有关向量数性积的等式证明问题。

结论

向量可以使图形量化,使图形间关系代数化，使我们从复杂的图形分析中解脱出来，只需研究这些图形间存在的向量关系就可以得出精确的最终结论，使分析思路和解题步骤变得简单流畅，又不失严密。解决立体几何问题，“平移是手段，垂直是关键”。合理运用向量解决立体几何问题，在很大程度上避开了思维的强度转换，避开了添加辅助线，代之以向量计算，立体几何问题变的思路畅通，运算简洁。

［1］胡源艳，梁燕来，易亚利，凌征球.巧用代数方法解决解析几何中的某些问题［J］.玉林师范学院学报，2011，（02）：42-45.

［2］周宁，夏益斌.行列式在解析几何中的应用［J］.昆明冶金高等专科学校学报，2011，（01）：60-61.

［3］张培强.对一道解析几何试题的几何探析［J］.数学通讯，2010，（19）：30-31.

［4］刘润东，包立巍.点在圆锥曲线“内部”的作用［J］.教育教学论坛，2011，（08）：185-186.

［5］乌仁.谈解析几何中参变量的范围问题［J］.赤峰学院学报（自然科学版），2006，（04）：32-33.

［6］陈蓬碧.一类解析几何最值问题的探讨［J］.四川职业技术学院学报，2008，（02）：104.

［7］朱瑾.浅谈解析几何的发展及其简单应用［J］.科技信息，2009，（18）：73.

［8］彭刚，陈坤明.多元视角下的 Urquhart定理［J］.四川教育学院学报，2009，（07）：115-116.