类比法在概率论教学中的应用研究
杨 芳
(长治学院 数学系,山西 长治 046011)
《概率论》是大学数学的一门重要的基础课。它不同于高等数学、线性代数等研究确定性现象的数学分支,有其鲜明的特殊性。一方面,教学内容概念多而且抽象独特;另一方面,公式多而且复杂难懂[1]。因此,在教学中,常常使初学者感到畏惧,教师也感到难教。如何提高教学质量成为一线教师急切探讨、思考的问题。
类比法是一种比较不同事物的相同点的逻辑思维方法,是立足于已有知识来认识新知识的一种创新性、有效性的方法[2]。利用已知的概念、公式及定理来引入新知识,不仅可以温故知新,还有化难为简之功效,使学生易于接受。因此,在教学中科学合理地使用类比法,可使学生在学习过程中触类旁通、启发思想,以形成良好的认知结构。
1 随机事件与集合的类比
随机事件是概率的研究对象,也是概率论课程中引入的第一个概念,对它的掌握情况将直接影响后续的学习,因此,随机事件的学习至关重要。随机事件是样本空间的子集,而样本空间是随机试验所有可能结果的集合[3]。因此,随机事件实际上就是集合,随机事件间的关系及运算与集合论中集合的关系及运算是完全相似的。

表1 随机事件与集合的类比
表1是概率论与集合论中的一些术语的对照。此外随机事件的运算律:交换律、结合律、分配律和对偶律都与集合的运算律完全相同。因此,在教学中如果讲清这两者的联系,一方面学生容易进入新课程的学习,而且学生能顺利掌握随机事件的内容,为后续学习奠定了坚实的基础。
2 离散型随机变量与连续型随机变量的类比
离散型随机变量与连续型随机变量是两类重要的随机变量。分布律Pk是离散型随机变量的重要函数,概率密度f(x)是连续型随机变量的重要函数。表面上看这两类随机变量有很大的区别,实际上,两者没有质的区别。两者的联系与区别主要在于求和与积分的联系与区别。而积分本质上是和式的极限。因此,两者许多方面可以统一起来。
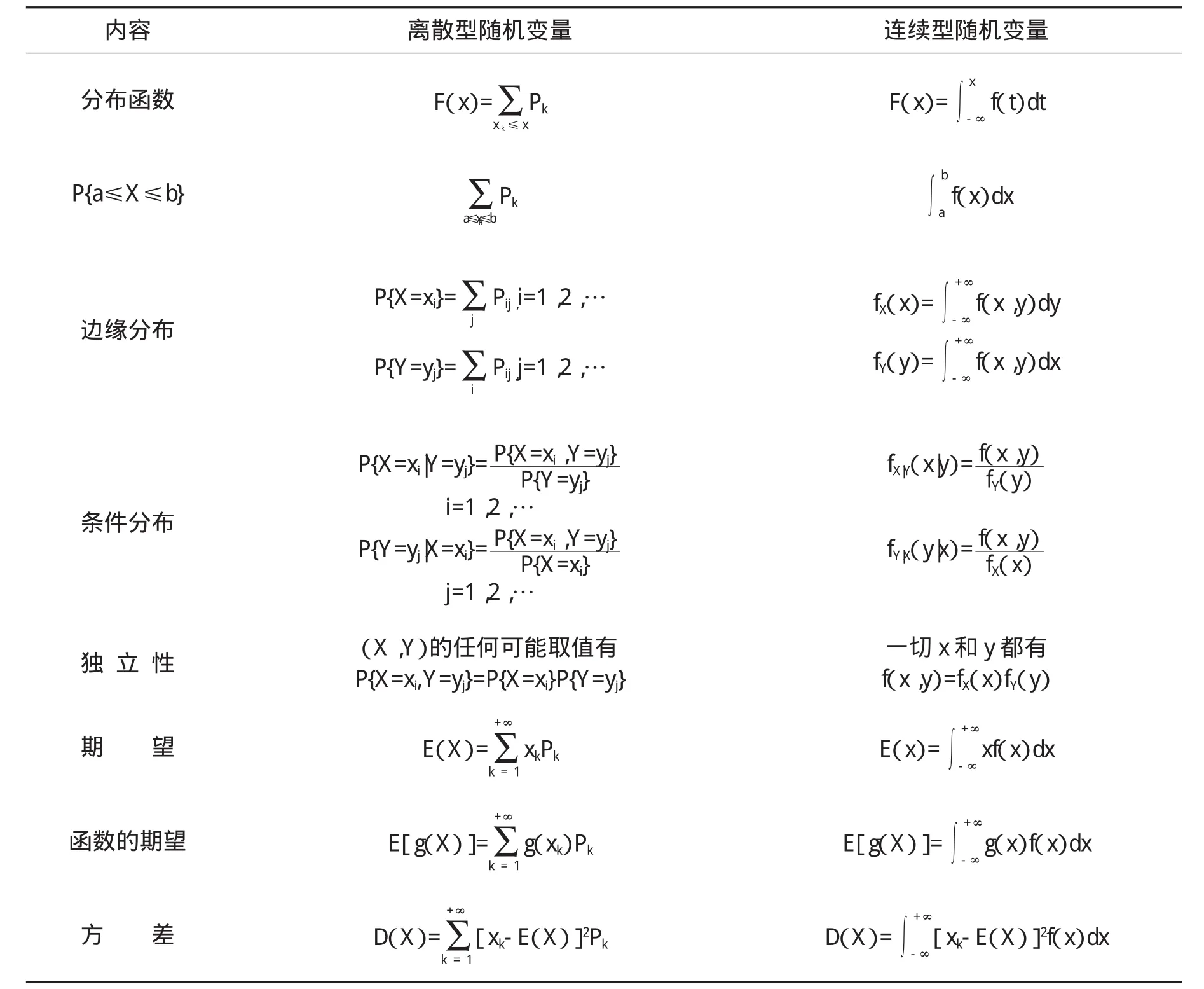
表2 离散型随机变量与连续型随机变量的类比
3 一维随机变量与二维随机变量的类比
在实际应用中,有时只用一个变量是难以描述的,需要引入多个变量加以描述,因此,需要学习多维随机变量,其中主要学习二维随机变量。一维随机变量与二维随机变量的联系与区别主要在于一次与二次的联系与区别。
4 大数定律之间的类比
大数定律是概率论的基本理论,证明了在大样本的条件下,样本均值可以看作是总体期望,这为概率论与数理统计的研究和应用提供了可靠的理论依据。但是由于大数定律本身理论性较强、内容复杂、结构奇特,使其成为概率论教学的难点。
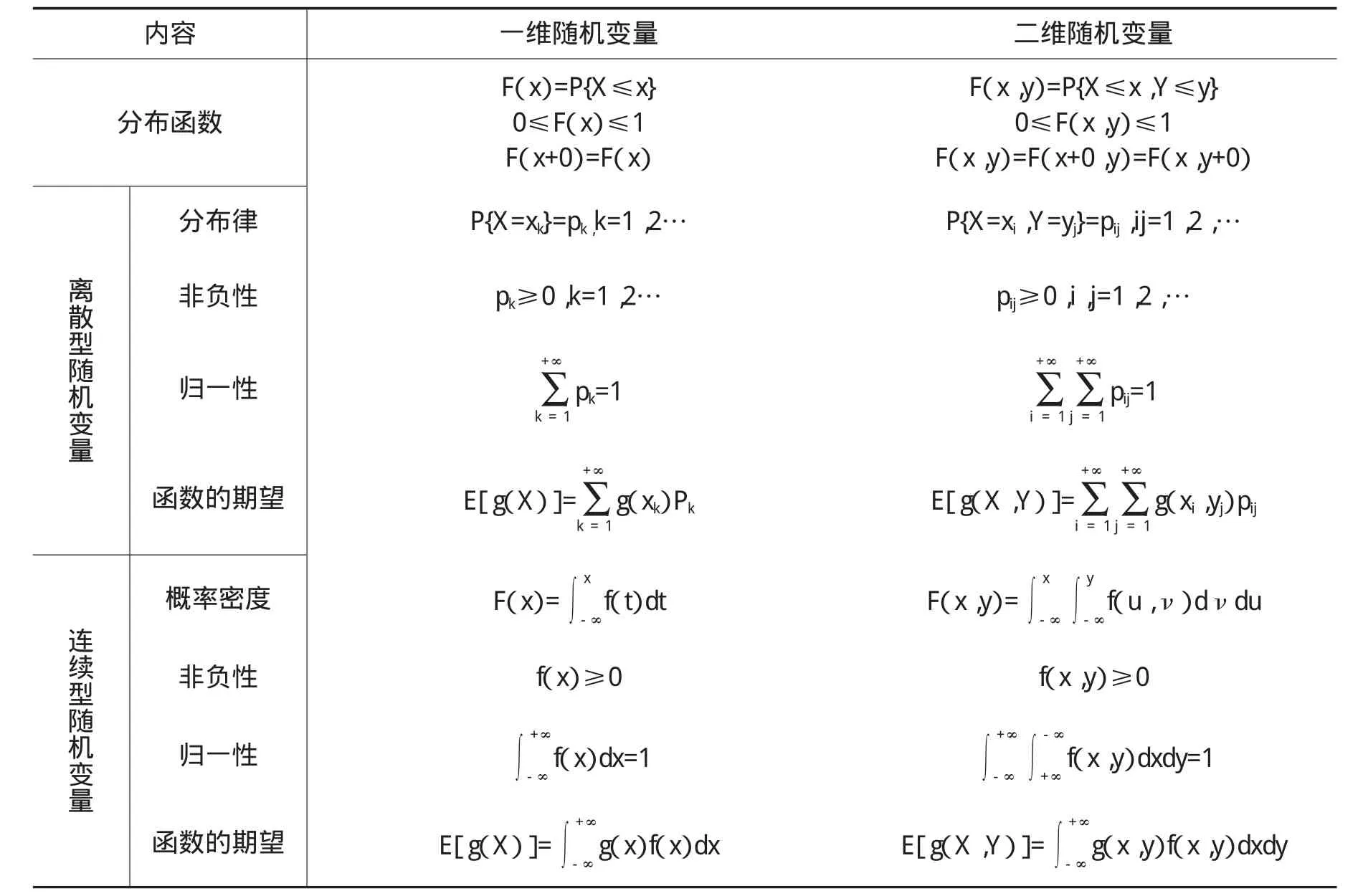
表3 一维随机变量与二维随机变量的类比
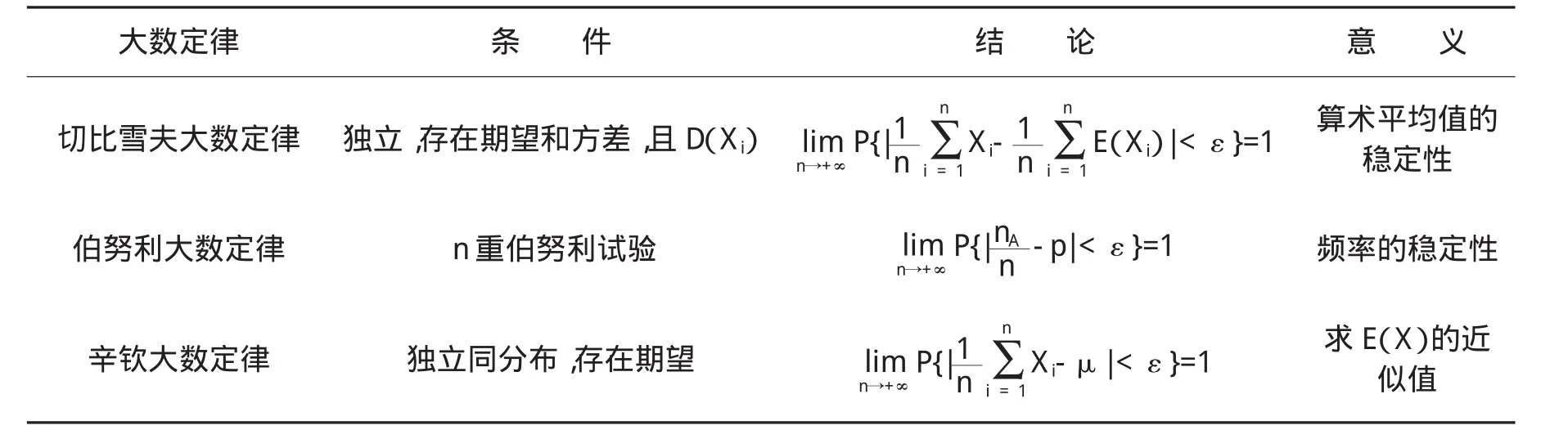
表4 大数定律间的类比
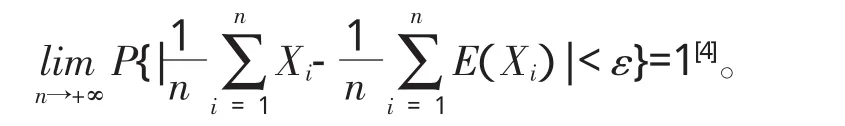
《概率论》是一门比较难学又难教的数学课程。教学实践表明,在不同教学环节中灵活运用类比法,可以在一定程度上减轻教师的教学负担和学生的学习负担。不仅可以提高教学效果,而且可以培养学生判断推理的能力和创造性思维的能力。
[1]邓华玲,傅丽芳.概率论与数理统计课程的改革与实践[J].大学数学,2004,20(1):34-37.
[2]汪小黎.运用心理规律增强“概率统计”教学的实效性[J].高等数学研究,2010,13(3):47-49.
[3]韩旭里,谢永钦.概率论与数理统计[M].上海:复旦大学出版社,2010.
[4]盛骤.概率论与数理统计[M].北京:高等教育出版社,2001.

