水下滑翔器整体外形设计及水动力性能分析

孟凡豪，严天宏，何 波，徐新胜

(1.中国计量学院机电工程学院，浙江杭州 310018;2.中国海洋大学信息科学与工程学院，山东青岛025506)

水下滑翔器(AUG，Autonomous Underwater Glider)是20世纪90年代以浮标技术为基础发展起来的新型水下测量仪器搭载平台［1］。与传统的水下自航行平台相比较，其具有航程大，低噪声，低成本等优势。近年来，随着海洋监测和海洋开发的需求增长，水下滑翔器的研究与应用前景得到了海洋研究领域的充分认识，并广泛地开展起来［2-4］。目前可以成功进行实际运用的水下滑翔器主要有三大类型:Scripps海洋研究所研制的Spray滑翔器，华盛顿大学设计的Seaglider滑翔器，Webb公司生产的Slocum滑翔器。这3种滑翔器的航程都超过了2 000 km，水下续航时间达到百余天，甚至1年［5-9］。

现在水下滑翔器的驱动方式有依靠浮力驱动、电能驱动、温差驱动，还出现利用太阳能驱动的水下滑翔器［10-11］。根据水下滑翔器工作环境的不同采用不同的驱动方式，这些都是为了提高水下滑翔器的水下速度、延长续航能力等特性。通过查阅资料了解到，现在的水下滑翔器很难同时满足高速、长续航时间这两个主要性能指标。水下滑翔器的经济性和稳定性是目前研发人员最关注的问题之一。减小水下滑翔器的俯仰力矩，提高升阻比，是现阶段提高水下滑翔器经济性和稳定性的主要手段。

基于CFD方法，对水下滑翔器的主体进行了设计仿真，通过不同构型主体的水动力仿真对比，获得最优外形;同时，还对水下滑翔器的附体机翼和尾翼进行了翼型的选择及设计，进一步提高了水下滑翔器的水动力特性;对设计后的水下滑翔器进行了整体的水动力分析，并与Slocum等几种经典水下滑翔器样机模型进行了性能比较，获得在特定攻角范围内的最佳升阻比，同时验证了新的水下滑翔器模型的水动力性能有了很大的提升。

1 主体设计及选择

1.1 主体模型的建立

水下滑翔器的基本功能相差不大，已有水下滑翔器的总体质量大约为50～70 kg左右。设计的目标水下滑翔器总质量定在60 kg左右。

根据水下滑翔器的质量M，初步估算滑翔器在水中的排水量:

滑翔器的主体外形大体定为长2 m，主体直径0.2 m。下面有五种主体外形设计构型，在选择时要充分考虑主体的水动力性能、可加工性以及内部空间的可利用性。如图1～图3所示，构型Ⅰ到构型Ⅲ是基于Slocum水下滑翔器样机在已有的尺寸上进行修改得到的［12-13］。

图1 AUG1主体构型IFig.1 Body Type I

图2 AUG2主体构型IIFig.2 Body Type II

图3 AUG3主体构型IIIFig.3 Body Type III

构型Ⅰ:主体两端采用直径为0.2 m的半球体，中间部分是直径为0.2 m，长为1.8 m的圆柱体，如图1所示。该构型的主要特点是结构加工简单，成本低，空间有效利用率较高，但是水动力特性很差。

构型Ⅱ:主体的首端依然是直径为0.2 m的半球体，尾端修正为偏心率e为3.5的半椭圆体，中间部分为直径0.2 m的圆柱体，如图2所示。该构型的主要特点是相对构型1其水动力特性得到了一定的提高，但是加工复杂性增加，内部空间有效利用率下降。

构型Ⅲ:主体首端修正为偏心率e为3的半椭圆体，尾端为偏心率e为3.5的半椭圆体，中间部分为直径0.2 m的圆柱体，如图3所示。该构型进一步提升了水下滑翔器的水动力特性，但在加工、有效空间利用等方面的性能被进一步的削弱。前3种构型是水下滑翔器现在应用比较广泛的几种主流主体外形，综合其特点为加工简单、成本低廉、空间利用率较高，有较好的水动力性能。

构型Ⅳ:依据标准椭圆线性方程设计的头尾对称的双参数椭圆回转体作为水下滑翔器的主体，其长短轴分为1.8和0.24 m，如图4所示。该构型在滑翔器的水动力性能和有效空间利用上都有很大的提升空间。

构型Ⅴ:采用NACA0012流线型线性方程设计的“雨滴”状回转体，其长度为2 m，最大直径为0.24 m，如图5所示。该构型与前三种构型相比较，其外形可以推迟边界层分离、减少漩涡阻力，使水下滑翔器的水动力性能有很大的提高，相对不足之处是有效空间利用有所下降。用“雨滴”状回转体作为水下滑翔器的主体是一个积极而有益的探索。

图4 AUG4主体构型IVFig.4 Body Type IV

图5 AUG5主体构型VFig.5 Body Type V

下文采用计算流体力学软件Fluent©分别对上述五种主体构型进行水动力计算与分析，通过综合对比分析得到最优结果。

1.2 网格的划分及计算条件的设定

滑翔器在水下航行时，以雷诺数来判别流动状态，雷诺数的定义公式为

式中:ρ为流体密度，v为入流速度，L为流体特征长度，μ为流体粘性系数。对于外流场判断湍流的标准为［14］:外掠平板时雷诺数Re大于5×105，外掠障碍物时大于2×104。这五种构型中，雷诺数Re在1.6×106左右，故为湍流。

网格划分采用非结构化网格，数量在100万到110万。在靠近水下滑翔器壳体的壁面处划分出一个小的区域并进行网格加密，这样可以保证网格疏密合理分布，又能减少总体网格数目，在不降低准确度的条件下可以加快计算速度。

计算条件的设定

1)计算区域为长12 m，半径3 m的圆柱体区域，边界条件为速度入口，压力出口。计算区域是模型的六倍，可以充分模拟流场环境，提高数值模拟的准确性，同时采用压力出口条件，这样可以考虑回流情况，使计算更容易收敛。

2)水下滑翔器的所有壁面均设定为静止无滑移壁面，壁面粗糙度为0，其它壁面均为无滑移壁面。流体材料设定为水密度998.2 kg/m3，运动粘性0.001 003 kg/m·s。

3)采用三维单精度压力基求解器，压力基求解器主要用于低速不可压缩流动的求解，密度求解器收敛速度快，但需要更多的内存和计算量，这里考虑到计算的是一个低速不可压缩流场，网格的数量很大，故采用压力基求解器。湍流模型选取为RNG k-ε模型，RNG k-ε模型考虑了湍流漩涡，RNG理论提供了一个考虑低雷诺数流动粘性的解析公式，这些特点使得RNG k-ε模型比标准k-ε模型等在更广泛的流动中有更高的可信度和精度［4］。

4)压力-速度耦合采用SIMPLE方法;离散格式中压力采用PRESTO离散，动量方程中的对流项采用二阶迎风差分格式，其余为一阶迎风差分格式。PRESTO离散可以保证计算的稳定性，二阶迎风差分格式可以提高计算精度，但是会增加计算量。所有参数的收敛残差标准为0.000 1。

1.3 模型数值计算准确性的验证

为了验证数值计算的合理性和准确性，按照上述方法计算的Slocum水下滑翔器在不同攻角下的阻力系数和文献［15-16］中的试验数据，对比如表1所示。由表1可知，数值计算结果和试验结果相近，文献［16］与试验结果最大误差为9.35%，本文最大误差为7.2%，完全满足计算的精度，验证了本文CFD模型的正确性与可靠性。

表1 针对阻力系数［15］CD本文数值模拟结果对比验证Tab.1 The comparison of the CDbetween the proposed numerical simulation and Reference［15］

1.4 模型数值计算收敛性的验证

为了验证数值计算的收敛性，计算模型2在速度为0.5 kn、攻角0°下的水动力值。所有参数的收敛残差标准为0.000 1。改变模型2的网格疏密程度，图6和图7分别是在80万网格和120万网格下，模型2的升力系数收敛曲线。从图6到图7可以看出，网格疏密不影响计算结果，迭代1 000次后升力系数不再变化，说明数值计算已收敛。

图6 80万网格时的模型2升力系数CL收敛曲线Fig.6 Lift CLconvergence curve for Model 2

图7 120万网格时模型2的升力系数CL收敛曲线Fig.7 Lift CLconvergence curve for Model 2

1.5 水动力性能的计算与分析

利用Fluent©的后处理功能可以计算出主体受到的阻力，无量纲化得到阻力系数。阻力系数和升力系数的计算公式分别为:

式中:ρ为水的密度;V为入流速度;Sd为主体的迎流截面面积或表面面积(选用不同面积时，阻力系数不同，这里选迎流截面面积计算);当计算的是机翼时，Sl为翼面的最大面积;L为升力;D为阻力。表2是五种方案主体在0.5 kn速度下的主要水动力参数。

表2 五种主体主要水动力参数Tab.2 The main hydraulic parameters of five body types

表2的计算结果表明:在速度为0.5 kn，攻角为0°的情况下，从构型AUG1到AUG5水下滑翔器主体构型的水动力性能不断提高，AUG4椭圆回转体与前三种主体构型相比，阻力分别减少了27%、10%、4%;AUG5“雨滴”状回转体与其他四种主体构型相比，阻力分别减少了33%、17.8%、12.2%和8.5%;这两种构型使水下滑翔器的阻力都有很大幅度的降低。图8是这五种主体构型在攻角为0°、不同速度条件下绘制的阻力曲线对比图。图8表明:随着水下滑翔器速度的增大，主体所受到的阻力也不断增大。通过对比可以看出AUG4、AUG5所受阻力的增长幅度始终低于其余三种主体，并且随着速度的增加，AUG4、AUG5的阻力增长幅度越来越小于其余三种主体的阻力增长幅度。AUG5“雨滴”状回转体的尾端比较狭长，使有效空间的利用率很低，加工难度较大;AUG4水动力性能良好，空间利用率较高，加工难度不大，综合考虑，这里选取AUG4作为水下滑翔器的主体。从图9、图10，可以分别看出AUG4主体构型的动压力分布和速度分布情况。

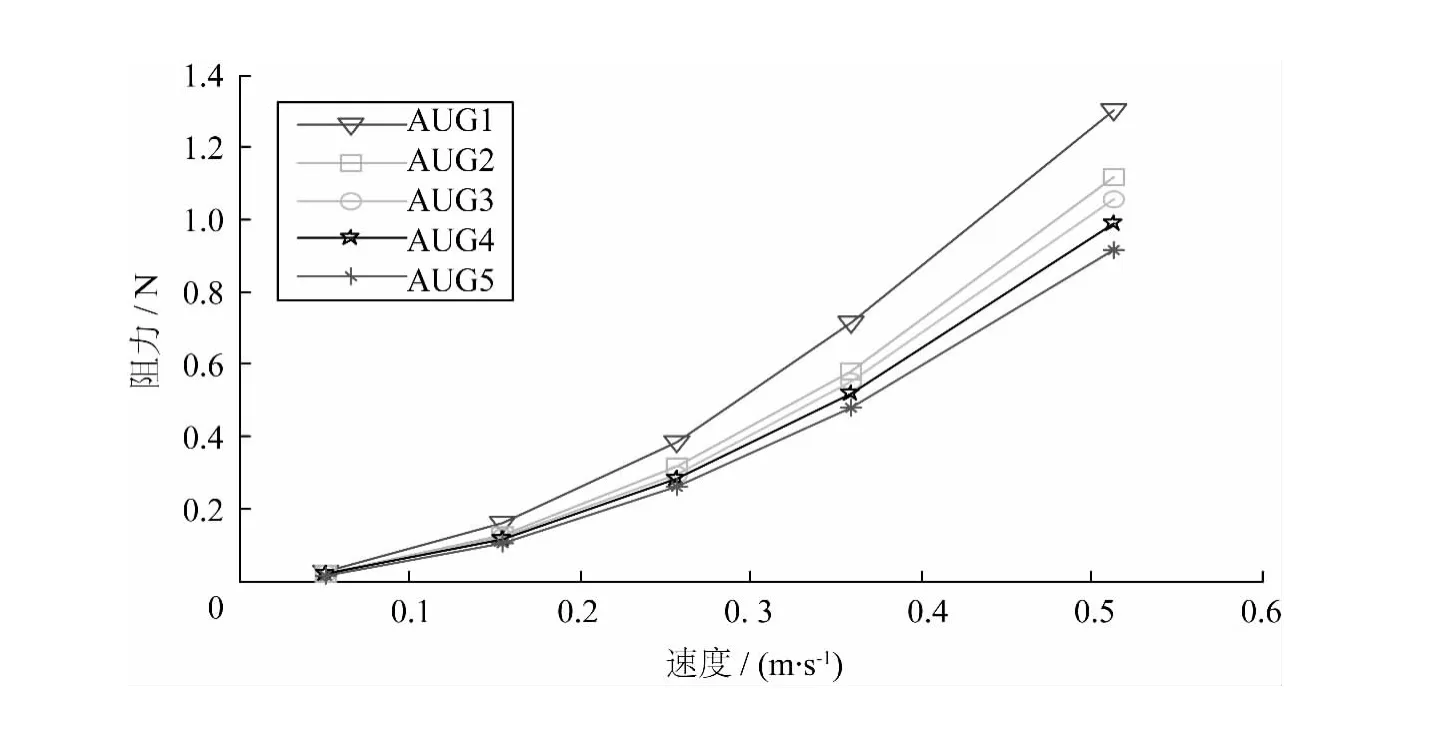
图8 攻角为0°不同速度下主体阻力曲线对比Fig.8 The drag force vs.the velocity with attack angle at 0°

图9 AUG4的动压(Dynamic Pressure)分布Fig.9 The distribution of dynamic pressure of AUG Type IV

图10 AUG4的二维速度矢量图Fig.10 The 2D velocity vector of AUG Body Type IV

2 附体设计及优选

水下滑翔器的附体包括机翼和方向尾翼。水下滑翔器要求滑翔机翼及方向尾翼在水下滑翔机的攻角、漂角范围内，尽量避免在翼上发生流动分离现象，以减少航行阻力和能耗。同时机翼应具备较大的升阻比，以提高两翼的工作效率。

2.1 机翼设计

2.1.1 翼型选择

因为水下滑翔机要在水中完成上浮和下潜运动，攻角会出现正负交替的现象，要保证在两种状态下翼型均有良好表现，选用对称翼型。低速的对称翼型可选用平板翼和曲面翼两种。

相关资料表明［17-18］:平板翼型的特点是型面简单、易于加工、成本低廉但相应的流体动力性能比曲面翼型差得多，易发生流动分离使阻力增大。而曲面翼型则相反，不易发生流动分离现象。因此，翼型的选择要在效率和加工工艺之间加以权衡从而决定采用哪种。为了研究两种翼型对升阻比的影响，采用Fluent©软件对面积相同的平板翼和曲面翼进行水动力模拟。图11是模拟水流速度为0.3 m/s，不同攻角下的两组翼型的升阻比变化曲线，显而易见，曲面翼的升阻比性能优于平板翼。通过图11对比可知，两种翼型的升阻比都会随着攻角的增大而提高，曲面翼的升阻比增大趋势明显大于平板翼，可以提高50%左右，其水动力性能更加优越，虽然加工相对复杂，但曲面翼仍会成为水下滑翔器的主流翼型。

2.1.2 机翼优选

目前水下滑翔器选择的曲面翼型基本为NACA系列翼型，本文将采用NACA0005翼型。在主体参数确定的情况下改变NACA0005机翼的翼展长l，梢弦长b1，后掠角λ，如图12所示。

图11 两种机翼升阻比随攻角变化关系曲线图Fig.11 The lift and drag ratio curves of 2 types of airfoils vs.the attack angle

图12 翼的平面形状［19］Fig.12 The planar shape of airfoil［19］

在攻角为6°，航速为0.3 m/s，根梢比η=2.5的情况下进行3因素3水平正交试验。正交试验法［16］可以得到设计参数的多种组合，使实验结果更加丰富，可以分析相应规律得到最优结果。正交参数仿真组合情况如表3所示。

表3 正交参数仿真组合表Tab.3 The orthogonal parameters combination for simulation

机翼对水下滑翔器经济性的影响，可以由滑翔器的升阻比L/D来评价［16］，升阻比越大，滑翔经济性越高。正交试验的组合模型，采用CFD软件进行水动力模拟仿真实验，得到每个模型的升阻比。正交试验结果如表4所示。

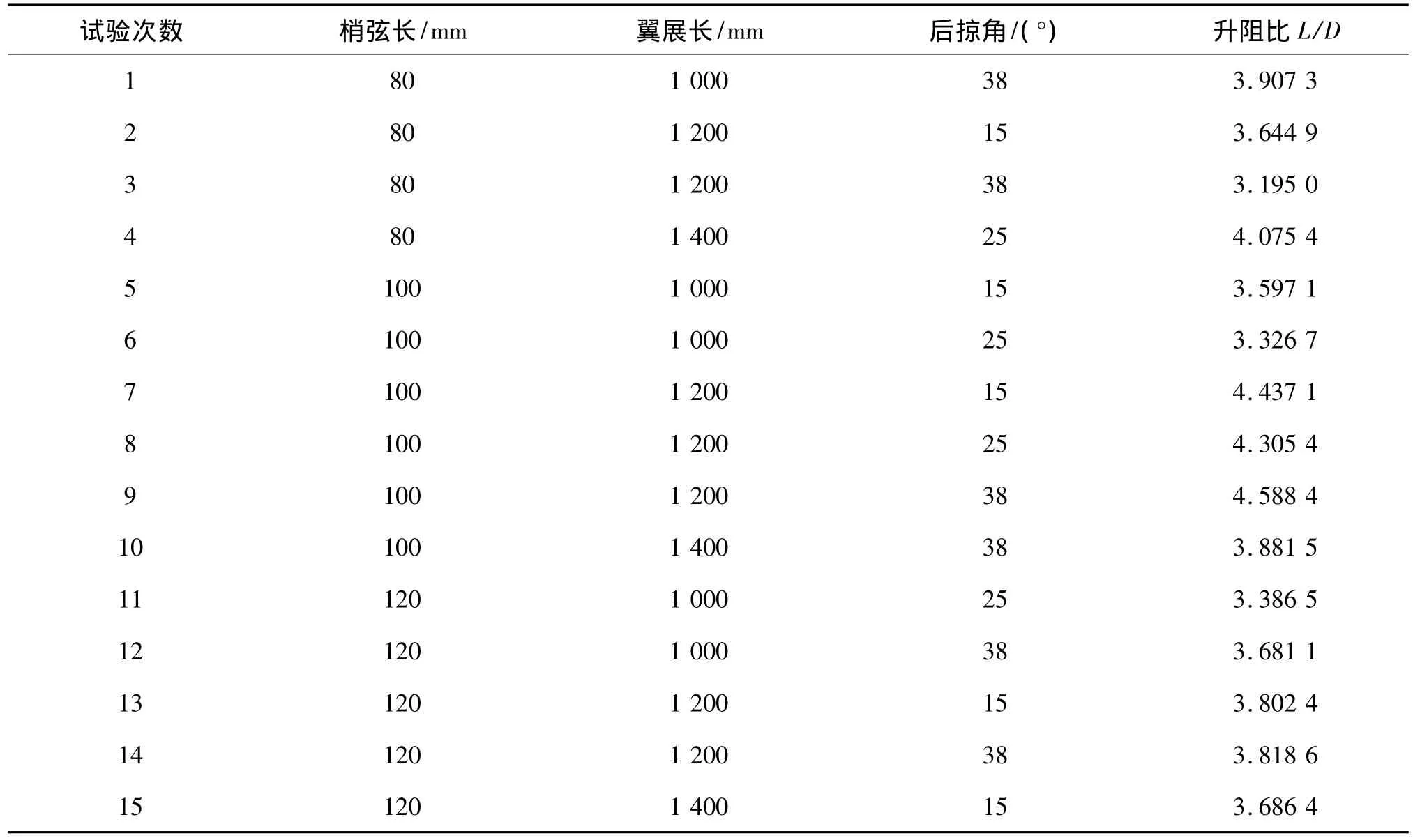
表4 正交参数表及仿真试验结果Tab.4 The orthogonal parameters and corresponding simulation results

正交试验结果表明，第4，7，8，9组翼型的实验结果与其他几组相比水动力性能提升很高。图13与图14是第9组机翼表面速度分布和压力分布情况。可看出第9组实验翼型能够有效避免翼上发生流动分离现象，以减少航行阻力、降低能耗;同时具有较大的升阻比，可提高两翼的工作效率。

图13 机翼表面速度分布Fig.13 The velocity distribution for airfoil

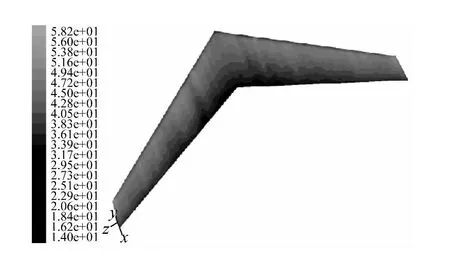
图14 机翼表面动压力分布Fig.14 The dynamic pressure distribution for airfoil

2.2 尾翼设计

尾翼的主要作用是保证水下滑翔器在最大速度及带攻角运动时具有足够的效率，通过与机翼配合产生的流体动力来提供水下滑翔器航向的稳定性。

根据文献［19］，尾翼选用NACA0024翼型，可以保证足够的效率和稳定性。尾翼的阻力效率受展弦比及后掠角的影响，选用较大展弦比及小后掠角尽量减小尾翼的阻力。

表5 尾翼后掠角性能比较Tab.5 The comparison of performances of different angles

翼展l=0.2 m，展弦比λ=2，根梢比η=1.6，根弦长 b0=0.16 m，梢弦长 b1=0.1 m。设定如表5中设计4个尾翼的后掠角方案，攻角为 0°，速度 0.3 m/s。利用Matlabc的曲线拟合工具，将阻力系数和后掠角的关系拟合为二次函数，并得到两者的经验公式，如图15所示。

由经验公式和图形以及表5得出结论:尾翼的后掠角在15°到20°之间阻力系数最小，考虑到加工和材料的因素，选择15°和20°作为较优值。

2.3 具体模型分析

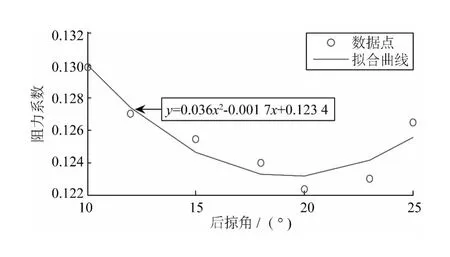
图15 阻力系数和后掠角的关系拟合曲线Fig.15 Relationship between CDand sweep angle

根据飞机的外形设计经验可知，从减小阻力的角度考虑，机翼最大横截面位置在机身长度的60%处最好。水下滑翔器机翼的最大横截面布置在主载体长度60%处，可获得最好的水动力性能。根据上述研究和分析结果，为进一步研究在不同航行攻角下附体对水下滑翔器的升阻比L/D和最大俯仰力矩 Mpitch的影响，对表5所示的5个具有不同机翼参数的具体模型进行航速为0.5 kn、攻角为0°～20°的数值模拟。升阻比L/D和最大俯仰力矩 Mpitch决定水下滑翔器的经济性和稳定性［16］。依据正交试验结果和尾翼后掠角性能比较结果，本文设计了5种水下滑翔器模型，这5种模型是由正交试验第4，7，8，9组实验翼型和尾翼模型中的方案2和3组合而成，具体模型参数如表5所示。图16和图17分别是模型2和模型3的外形效果图。图18为8°攻角下模型2的表面速度矢量分布图，图19为8°攻角下模型3的表面动压力分布云图。各模型其他参数的模拟结果比较如图20和图21所示。

图16 模型2的外形效果图Fig.16 The shape of Model 2

图17 模型3的外形效果图Fig.17 The shape of Model 3

图18 模型2的表面速度矢量分布图Fig.18 The velocity distribution for Model 2

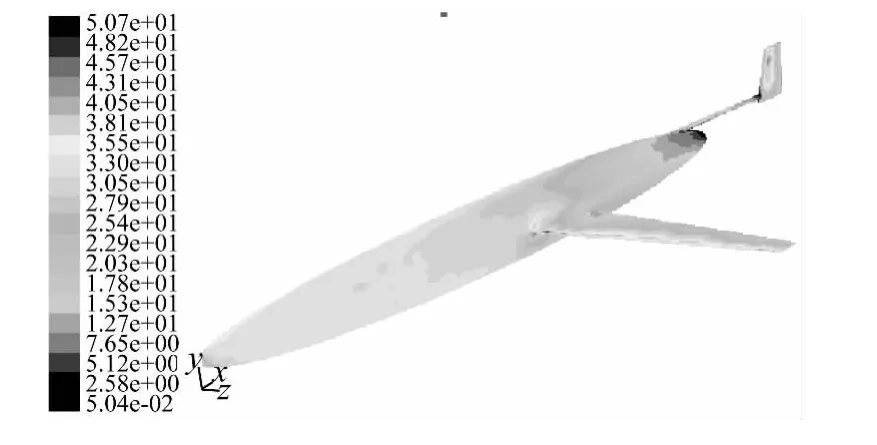
图19 模型3的表面动压力分布云图Fig.19 The dynamic pressure distribution for Model 3

表6 具体模型参数Tab.6 Parameters of specific models

由表6和图19中的模型1、模型2、模型3和模型5可知，水下滑翔器的升阻比L/D随着翼展的增加而增加，而随着后掠角的增大而下降;在上面机翼的正交试验中，机翼的升阻比L/D随着后掠角的增大而增大，由此可推知，单独进行水动力性能分析最优的机翼不能确保水下滑翔器整体的水动力性能达到最优。由图21中的模型1、模型2和模型5可知，水下滑翔器的最大俯仰力矩 Mpitch随着后掠角的增加而减小，即稳定性增加，机翼的重心位置越靠后其稳定性越高。由图20和图21中的模型4和模型5可知，在低攻角范围内，水下滑翔器的升阻比L/D随着尾翼后掠角的增大而减小，当攻角超过6°后，随着尾翼后掠角的增大而略微增大;水下滑翔器的最大俯仰力矩 Mpitch随着尾翼后掠角的增大而增大，即稳定性下降。

由图20可知，模型3的升阻比明显大于其余模型，模型1和模型2的升阻比值相近，模型2整体上略微优于模型1。模型3的升阻比与模型2、模型4和模型5相比提高了4.4%、9%和10%，模型2与模型4和模型5相比提高了4.5%和4.8%。而由图21可以看出，模型3的最大俯仰力矩大于其余模型，其稳定性下降明显。模型3的稳定性与模型2、模型4和模型5相比下降了19.8%、23%和24%。模型2与模型1最大俯仰力矩曲线基本相近，比模型4和模型5增大了4.3%和4.7%。

图20 升阻比L/D随攻角的变化关系Fig.20 Relationship between L/D and attack angle

图21 最大俯仰力矩 Mpitch随攻角的变化关系Fig.21 Relationship between Mpitch and attack angle

由上述分析可知，在滑翔状态下，为提高滑翔经济性应尽量增加机翼的翼展，同时减小机翼的后掠角，但为提高航行器的稳定性，又需要增大机翼的后掠角来实现。可见，提高滑翔器滑翔经济性和增加稳定性这两方面是矛盾的，设计需要根据其他性能要求来选择。

3 具体模型与样机水动力性能对比分析

为进一步选取最优模型，将模型2和模型3与Spray、Seaglider、Slocum这三种经典水下滑翔机相比较，它们机体尺寸和重量相差不多，体长2～3 m左右，重量约为50～70 kg，根据Spray、Seaglider、Slocum水下滑翔机的外形设计参数［20-21］，可得到这三种样机模型，如图22～图24所示。这里通过CFD模拟仿真，获得三种经典样机的水动力性能参数，其数据可靠性已经在上文中验证。模型2和模型3与这三种样机在航速0.5 kn，不同的攻角下进行水动力性能分析对比，具体仿真参数和指标见表7。

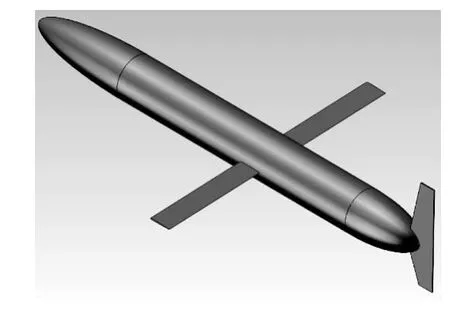
图22 模型 I——Spray样机Fig.22 The classic type I-Spray Model

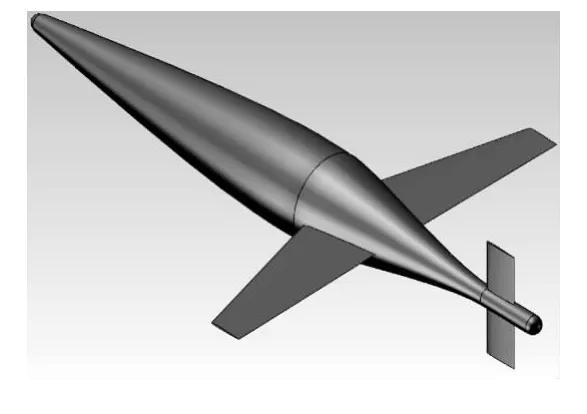
图23 模型II——Seaglider样机Fig.23 The classic type II-Seaglider Model

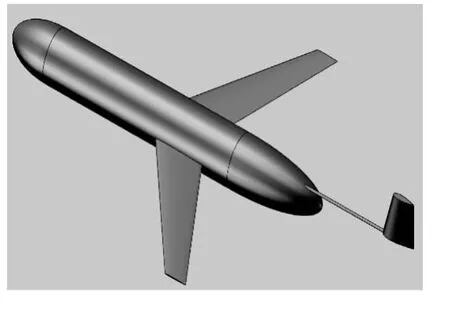
图24 模型III——Slocum样机Fig.24 The classic model III-Slocum Model

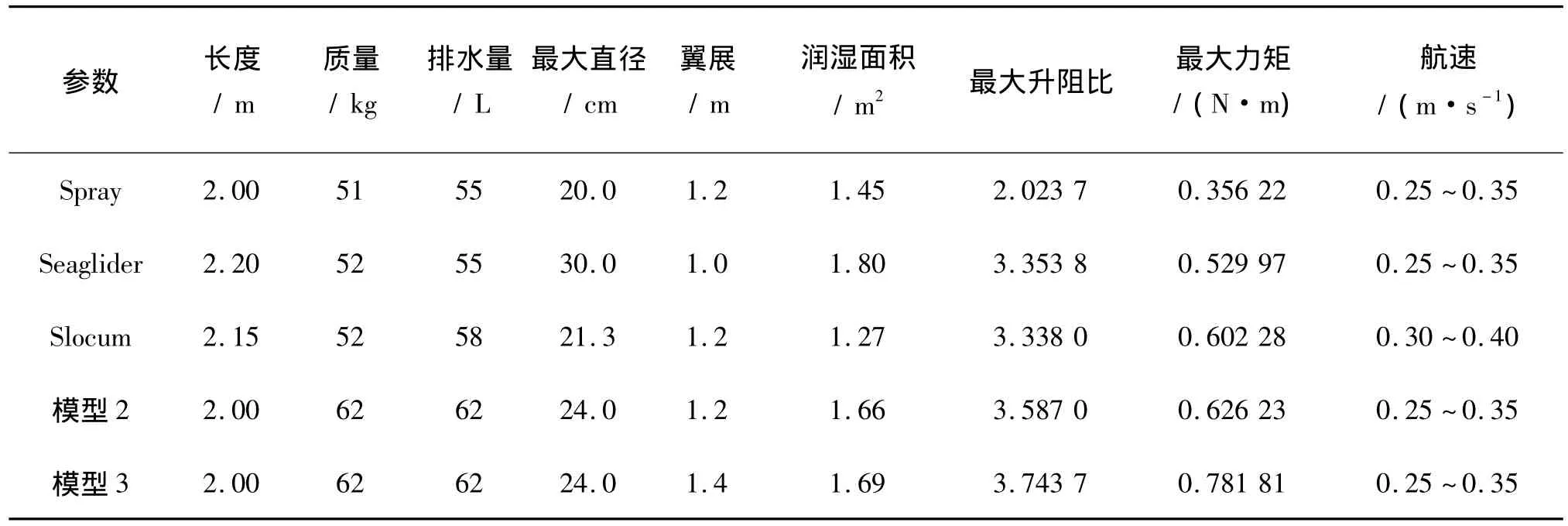
表7 模型2和模型3与样机主要参数对比Tab.7 The comparison of main parameters between the specific models and the classic types

图25 航速为0.5 kn不同攻角下具体模型和样机升阻比曲线对照Fig.25 The L/D ratio comparison between the specific models and the classic type under different attack angles

通过表7可知，模型2、模型3和三种主流样机相比较，排水量相对增加明显，增加了机体的内部空间;最大升阻比提升很大，使水下滑翔器具有更好的经济性，但是最大俯仰力矩增大，降低了水下滑翔器的稳定性。图25是航速0.5 kn，不同攻角下具体模型和样机升阻比曲线对照图。由图25中可知，模型2和模型3的升阻比在0°～40°的攻角范围内一直大于样机，两个模型的水动力性能提升非常明显，均满足设计要求。同时，模型2和模型3在攻角8°左右时具有最大的升阻比，故在8°左右攻角时具有最好的滑翔经济性。表8是模型2、模型3和样机达到最大升阻比时的水动力参数对照表。

表8 模型2和模型3与样机最大升阻比时水动力参数对照表Tab.8 The hydraulic performance comparison of specific models and the classic model with maximal L/D ratio

为了综合考虑升阻比和俯仰力矩这两个影响水下滑翔器水动力性能的因素，本文引用文献［22］中的加权公式:

式中:FL(X)、FD(X)和 Mpitch( X )分别是水下滑翔器在攻角8°受到的升力、阻力和最大俯仰力矩，ω1和ω2是加权系数。

为了能够保证持续高效航行，一般会让水下滑翔器的攻角长时间保持在最大升阻比时的角度，这时水下滑翔器具有最佳滑翔经济性，因此水下滑翔器在这一角度的稳定性也尤为重要。利用加权公式综合考虑这两大因素，获得的加权值，如表8所示。其中模型2的加权值最高，即模型2的综合水动力性能最优。以上数据分析表明，模型2在保持长时间航行时具有更高的航速以及工作效率。

4 结语

在Slocum等几种典型水下滑翔器样机的基础上，对主体及其附体机翼和尾翼进行了设计，得到了一种全新的水下滑翔器外形，它的水动力性能相比于Spray、Seaglider、Slocum三大主流样机有了大幅度的提升。当滑翔器在8°左右攻角航行时，具有最大的升阻比，可以保证其在水下长时间高效率航行，并且能满足工程设计和研究的要求。

［1］ Daneil L Rudnick，Russ E Davis，Charles C Eriksen，et al.Underwater gliders for ocean research［J］.Marine Technology，Society Journal，2004，38(1):48-59.

［2］ 张宏伟，李智，王延辉，等.水下滑翔器浮力驱动机构布局分析［J］.海洋技术，2009，28(1):1-4.(ZHANG Hong-wei，LI Zhi，WANG Yan-hui，et al.Research on the layout of the buoyancy engine of underwater glider［J］.Ocean Technology，2009，28(1):1-4.(in Chinese))

［3］ 王树新，王延辉，张大涛，等.温差能驱动的水下滑翔器设计与实验研究［J］.海洋技术，2006，25(1):1-5.(WANG Shu-xin，WANG Yan-hui，ZHANG Da-tao，et al.Design and trial on an underwater glider propelled by thermal engine［J］.Ocean Technology，2006，25(1):1-5.(in Chinese))

［4］ 张奇峰，俞建成，唐元贵，等.水下滑翔机器人运动分析与载体设计［J］.海洋工程，2006，24(1):74-78.(ZHANG Qi-feng，YU Jian-cheng，TANG Yuan-gui，et al.Motion analysis and body design of an underwater glider［J］.The Ocean Engineering，2006，24(1):74-78.(in Chinese))

［5］ Douglas C W，Paul J S，Clayton P J.SLOCUM:An underwater glider propelled by environmental energy［J］.IEEE Journal of Oceanic Engineering，2001，26(4):447-452.

［6］ Eriksen C C，Osse T J，Light R D，et al.Seaglider:A long range autonomous underwater vehicle for oceanographic research［J］.IEEE Journal of Oceanic Engineering，2001，26(4):424-436.

［7］ Sherman J，Davis R E，Owens W B，et al.The autonomous underwater glider“Spray”［J］.IEEE Journal of Oceanic Engineering，2001，26(4):437-446.

［8］ Davis R E，Eriksen C E，Jones C P.The technology and applications of autonomous underwater vehicles［M］.Griffiths Ged.London:Taylor and Francis，2002.

［9］ Dr Stephen Wood，P E ToddAllen，Sean Kuhn Joseph Caldwell.The Development of an autonomous underwater powered glider for deep-sea biological，chemical and physical oceanography［C］//OCEANS 2007-Europe.IEEE Journal of Oceanic Engineering，2007:1-6.

［10］ Chappell S G，Komerska R J，Blidberg D R，et al.Recent field experience with multiple cooperating solar-powered AUVs［C］//The Fifteenth International Symposium on Unmanned Untethered Submersible Technology.IEEE Journal of Oceanic Engineering，2007:1-8.

［11］ Arima M，Okashima T，Yamada T.Development of a solar-powered underwater glider［C］//Underwater Technology(UT)，2011 IEEE Symposium on and 2011 Workshop on Scientific Use of Submarine Cables and Related Technologies(SSC).IEEE Journal of Oceanic Engineering，2011:1-5.

［12］ Alvarez A.Redesigning the SLOCUM glider for torpedo tube launching［J］.IEEE Journal of Oceanic Engineering，2010，35(4):984-991.

［13］张禹，李雀屏，杨国哲，等.水下滑翔机器人载体外形设计与优化［J］.机械设计与制造，2010，10:148-150.(ZHANG Yu，LI Que-ping，YANG Guo-zhe，et al.Design and optimum shape of underwater glider［J］.Machinery Design ＆ Manufacture，2010，10:148-150.(in Chinese))

［14］李鹏飞，徐敏义，王飞飞.精通CFD工程仿真与案例实战［M］.北京:人民邮电出版社，2011.(LI Peng-fei，XU Min-yi，WANG Fei-fei.Fluent gambit icem CFD tecplot［M］.Beijing:Posts ＆ Telecom Press，2011.(in Chinese))

［15］Joshua G G，Ralf B，Naomi E L.Underwater glider model parameter identification［C］//13th Unmanned Untethered Submersible Technology(UUST).2003:1-12.

［16］武建国，陈超英，王树新，等.混合驱动水下滑翔器滑翔状态机翼水动力特性［J］.天津大学学报，2010，43(1):84-89.(WU Jian-guo，CHEN Chao-ying，WANG Shu-xin，et al.Hydrodynamic characteristics of the wings of hybrid-driven underwater glider in glide mode［J］.Journal of Tianjin University，2010，43(1):84-89.(in Chinese))

［17］胡克，俞建成，张奇峰.水下滑翔机器人载体外形设计与优化［J］.机器人，2005，27(2):108-113.(HU Ke，YU Jian-cheng，ZHANG Qi-feng.Design and optimization of underwater glider shape［J］.Robot，2005，27(2):108-113.(in Chinese))

［18］王强，葛彤，吴超，等.结合固定翼飞机原理重水潜器设计［J］.海洋工程，2012，30(2):143-149.(WANG Qiang，GE Tong，WU Chao，et al.Design of the HUV based on the airplane's principles［J］.The Ocean Engineering，2012，30(2):143-149.(in Chinese))

［19］诸敏.水下滑翔机设计优化与运动分析［D］.杭州:浙江大学，2007.(ZHU Min.Optimizing＆kinetic study of underwater glide［D］.Hangzhou:Zhejiang University，2007.(in Chinese))

［20］ Daniel L R，Russ E D，Charles C E，et al.Underwater gliders for ocean research［J］.Marine Technology Society Journal，2004，38(1):48-59.

［21］ Davis R E，Eriksen C C，Jones C P.Autonomous buoyancy-driven underwater gliders［C］//Technology and Applications of Autonomous Underwater Vehicles.London:Taylor＆ Francis，2002:37-58.

［22］谷海涛，林扬，胡志强，等.基于代理模型的水下滑翔机机翼设计优化方法［J］.机械工程学报，2009，45(12):7-14.(GU Hai-tao，LIN Yang，HU Zhi-qiang，et al.Surrogate models based optimization methods for the design of underwater glider wing［J］.Journal of Mechanical Engineering，2009，45(12):7-14.(in Chinese))