双浮床布设对河流水动力特性的影响模拟

李 勇，吴娅明，朱 亮，倪利晓，谭秋群

(1.河海大学浅水湖泊综合治理与资源开发教育部重点实验室，江苏南京 210098;2.河海大学环境学院，江苏南京 210098)

随着河道水污染日益严峻［1］，生态浮床技术被逐渐应用于水体修复中。像河道中植物能够改变河道水流形态进而导致水体中物质的运动轨迹产生变化一样［2-3］，生态浮床的组合布设也会改变河道局部的水流特征。朱红钧等［4］通过试验发现河道中布设椭圆柱形生态种植圈后纵向流速较布设前波动明显，相对紊动强度和雷诺应力略有增加;Atal等［5］分别对双圆柱、三圆柱串列和并列布置进行数值模拟，结果显示随着雷诺数的增大，双圆柱串列时圆柱间干涉效应比并列时更敏感;Summer等［6］将2个等直径的圆柱错开布置，通过改变圆柱之间的距离和关联角度，得出双圆柱错开布置的9种不同流态;盛奇伟［7］用Fluent软件模拟并列布置的双方柱绕流问题时发现间距比对流场的影响比雷诺数大，且间距比存在临界值。由此可见，国内外学者已对不同浮床形状及布置间距的水力特性有一定的研究。目前对于生态浮床净化机理的研究多从生态浮床系统中植物及填料对污染物的去除效果进行探讨［8-11］，而从水动力学角度进行研究的报道较少，马克星等［12］在论述现今生态浮床存在问题中指出了这一现象。

基于此，笔者在不考虑生态浮床填料及植物等内部结构的前提下，通过大型水槽试验和数值模拟，分析双方柱浮床在3种不同布置形式下水流流速及相对紊动强度的分布情况，为河道生态浮床技术措施的合理实施提供理论和设计依据。

1 试验方法

采用2个相同的正方形浮床(有机玻璃制成)进行不同布置形式下其对水流特征的影响研究。选取4种工况:无浮床布置(KB)、2个浮床平行于水流方向串列布置(CL)、垂直于水流方向并列布置(BL)和2个浮床与水流方向成45°错开布置(CZ)。浮床布置形式见图1，浮床边长D=13.3 cm，2个浮床中心距L=3D=33.9 cm，淹没深度h0=5 cm。模拟试验在室外矩形水槽内完成，水槽长31.7 m、宽1.2 m、高0.85 m，槽内水体通过单向潜水泵循环使用。水槽两侧壁是水泥面，底部为光滑水泥抹面，水槽坡降为0.001。

在控制进流量不变的情况下，通过调节水槽尾部插板来控制水位，平均水深调至约20 cm。浮床几何中心A布置在离水流入口12 m的断面M处，确保上游来流稳定。各点流速采用声学多普勒测速仪ADV测得。为掌握浮床对水动力特性的影响范围，设置6个监测断面B，C，M，E，F，G(图1)。断面上每隔10 cm布置1条垂线，共11条垂线;垂线上从水面下2.5 cm处水平面H开始布点，依次为水面下 0.5 h0，1.0 h0，1.6 h0，2.4 h0和 3.2 h0。

图1 浮床布置形式及监测断面示意图Fig.1 Schematic diagram of arrangements of floating beds and monitoring sections

2 数值模拟

2.1 模型控制方程

采用RNG k－ε模型，计算控制方程为连续性方程和动量方程:

连续性方程

动量方程

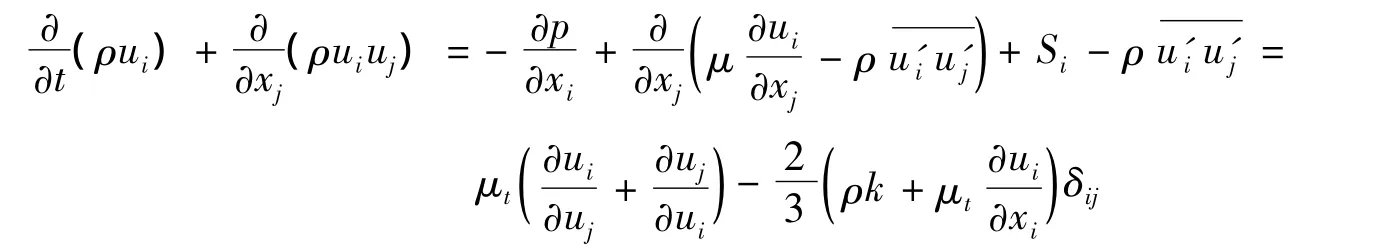
式中:ui——时均速度;xi——流体质点的空间位置;t——时间;ρ——流体密度;p——流体压力;μ——动力黏度;Si——广义源项;μt——湍动黏度;k——湍动能;δij——Kronecker delta 符号(当 i=j时 δij=1，当 i≠j时δij=0)。

将RNG用于动量方程并引入湍动能k和湍动耗散率ε，所得方程如下:

其中 μeff=μ +μt，μt=ρCμ常数Cμ=0.0845，C1ε=1.42，C2ε=1.68，ακ=αε=1.39，η0=4.377，β =0.012。

2.2 边界条件

流动入流边界流量为20.76 L/s;出口边界处流动得到充分发展，选用自由出流边界条件，则有=0φ=u，p，k，ε。固壁设为无滑移动边界条件，近壁区采用壁面函数法处理。自由水面采用刚盖假定，按对称面处理即各变量在法向方向的值和切向方向的梯度都为零。

2.3 求解方法

采用直接求解三维不可压黏性流体的RANS方程，微分方程的离散采用有限体积法，速度与压力的耦合求解采用SIMPLEC算法，压力项采用二阶离散格式，动量、湍动能及耗散率的离散均采用二阶迎风格式。

3 结果分析与讨论

3.1 模型率定

选取3种布置形式各断面水面下0.5 h0，1.6 h0和3.2 h0中垂线处实测流速与模拟值进行比较。如图2所示，实测值与模拟值误差保持在1%之内，说明数值模拟可以较好地模拟出浮床影响下的水动力特性。

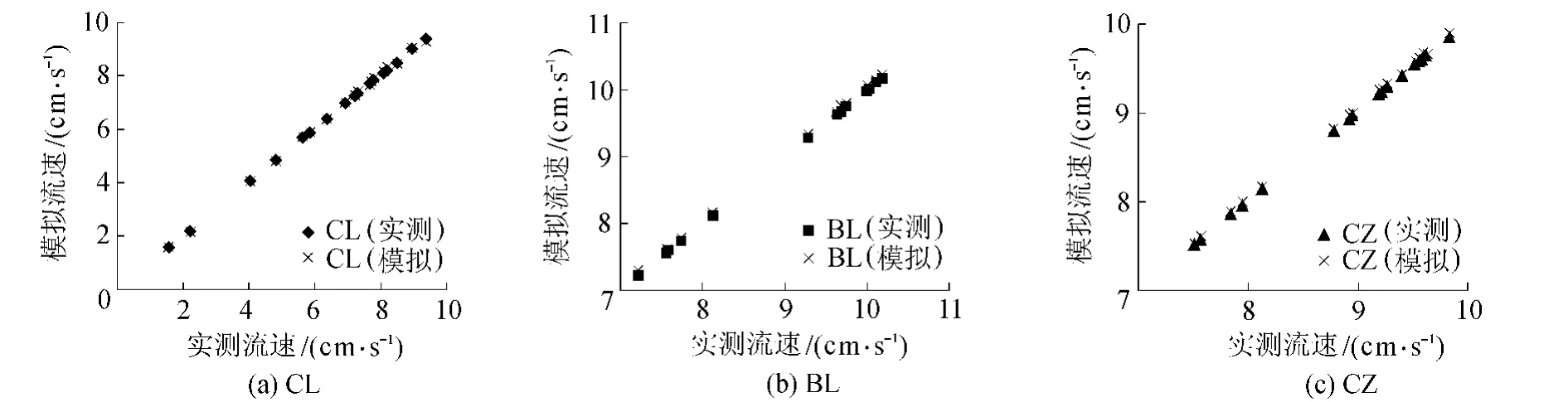
图2 3种布置形式实测与模拟的流速对比Fig.2 Comparison of observed and simulated velocities with three types of arrangements

表1为4种工况下各断面平均流速分布。总体上，浮床3种布置形式对下游断面流速的影响比上游大。在M断面，BL时平均流速远远大于CL和CZ的平均流速，主要由于BL时该断面横截面收缩，导致断面平均流速明显增大。

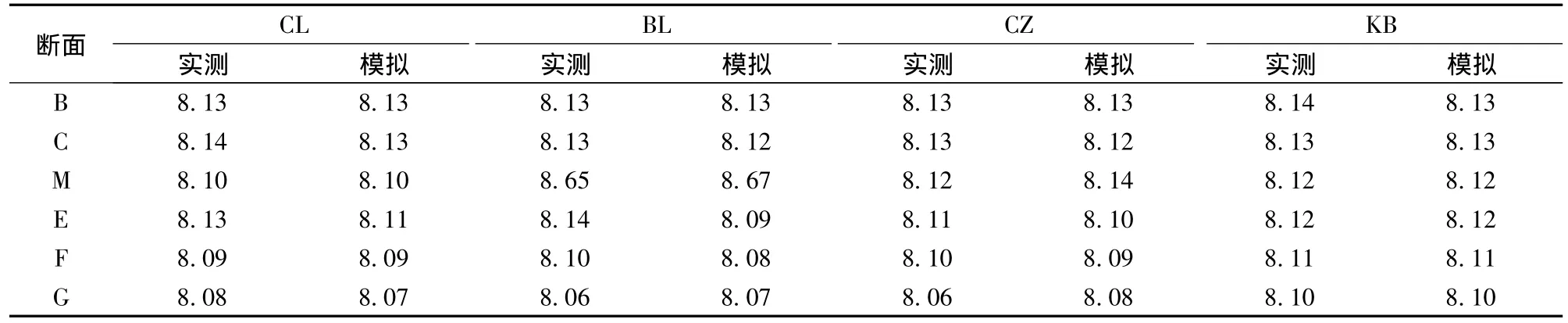
表1 断面平均流速分布Table 1 Distribution of average velocities at cross-sections cm/s

3.2 水平面H处流场分布及浮床影响范围

图3为双浮床3种不同布置形式在水平面H处的流速分布。总体上，水流在浮床前方受到阻碍，一部分直接流向浮床，在抵达时流速逐渐减小;另一部分绕浮床流过，随后边界层出现流体分离。在浮床后方由于负压的作用形成卡门涡街，并延伸至后方一定距离。(a)CL时，双浮床后都发生涡的分离，正后方均形成低速区;文献［13］指出两串列方柱的临界间距L/D=4.05，当间距小于临界值时前柱的涡街被抑制，两柱之间为速度很小的死水区域。本文的结果与其相符。(b)BL时，双浮床形成反相同步的漩涡，浮床间缝隙流不偏向任何一侧。饶勇等［14］在研究BL双方柱不同间距比流场特性时，同样得出当L/D＞1.5时流场开始转为对称流从而形成对称漩涡的结论。(c)CZ时，前浮床流动分离受到后浮床的抑制，导致前浮床的尾迹窄于后浮床，模拟结果与胡卫华［15］双圆柱CZ布置时的流场分布相似。

3种布置形式下，在H水平面上以与KB流场相比流速相差1%作为浮床影响范围的标准。CL、BL和CZ影响面积分别达到6.16 m2、5.66 m2和7.75 m2。在此影响范围内，CL、BL和CZ工况下H平面上的平均流速分别为8.97 cm/s、8.87 cm/s和8.74 cm/s，比KB时分别小1.12%、2.56%和4.24%。由此可见，CZ对水平面H的影响范围和平均流速较其他2种布置形式影响更大。

图3 浮床3种不同布置形式在水平面H处的流速分布云图(单位:m/s)Fig.3 Velocity distribution on horizontal plane H with three types of arrangements of floating beds(units:m/s)

3.3 浮床下游流速分布特征

图4为浮床3种布置形式在水平面H处下游E线、F线和G线上流速的变化特征。整体而言3种布局形式流速分布规律一致，CL、BL和CZ对下游的影响距离分别为4.7 m、4.43 m和6.08 m。CL时，E线、F线和G线处的平均流速比KB时分别小13.27%、7.78%和5.95%;BL时，E线、F线和G线的平均流速比KB时分别小13.59%、9.72%和7.46%;CZ时，E线、F线和G线处的平均流速比 KB时分别小16.94%、11.56%和10.59%。

E线、F线和G线上的流速除靠近壁面外，最小值即拐点均出现在浮床后方，主要受到浮床的阻挡作用。CL时，由于受到前后浮床的双重作用，使下游流速最小值在3种布置形式中最小，E线、F线和G线上流速拐点值分别为0.8cm/s、2.13cm/s和4.77cm/s，与KB相比分别小92.01%、78.82%和52.52%;BL时，出现2个等值对称的拐点值，E线、F线和G线上流速拐点值分别为3.76 cm/s、5.24 cm/s和6.29 cm/s，与KB相比分别小62.35%、47.57%和37.14%;CZ时，同样出现2个拐点，因布置不同，下游横向线更靠近右侧浮床，导致2个拐点值不一致，E线、F线和G线上左侧拐点流速值分别为5.4 cm/s、6.01cm/s和6.58 cm/s，与KB相比分别小46.16%、40.01%和34.32%，而E线、F线和G线上右侧拐点流速值分别为1.03 cm/s、2.6 cm/s和4.97 cm/s，与KB相比分别小89.72%、74.01%和50.4%。王远成等［16］在研究单方柱绕流时得出过方柱中心横向方向时均流速对称的结论，本文仅从单个浮床来看也具有此特征。杨纪伟等［17］利用FLUENT分别对双柱中心连线与流向夹角分别为90°、45°和0°(类似本文中的BL、CZ和CL)的流速分布进行模拟，给出了3种情况前柱中心线、后柱中心线和计算区域中心线速度分布图。将本文中拐点值位置及在浮床下游的变化趋势与之进行对比，结果一致。

图4 E线、F线和G线处的流速分布Fig.4 Velocity distributions of lines E，F，and G

3.4 相对紊动强度分布特征

水流的相对紊动强度等于紊动强度与相应断面时均流速之比，即T=/×100%。CL、BL和CZ在水平面H处影响范围内的相对紊动强度分别为11.52%、11.59%和9.48%，与KB相比分别大30.3%、31.1%和7.2%;同一水深，影响范围越大，相对紊动强度越小。

图5为双浮床3种布置形式在水平面H处下游E线、F线和G线处相对紊动强度的变化特征。KB时，E线、F线和G线处相对紊动强度平均值分别为9.03%、9.04%和9.06%;CL时，E线、F线和G线处相对紊动强度平均值分别比KB时大65.67%、54.2%和45.92%;BL时，E线、F线和G线处相对紊动强度平均值分别比KB时大91.03%、71.68%和57.06%;CZ时，E线、F线和G线处相对紊动强度平均值分别比KB时大76.08%、50%和42.16%。

由此可见，BL对水平面H和下游的平均相对紊动强度较其他2种布置形式大。由于水体中污染物紊动扩散参数和相对紊动强度呈一定正比例关系［18－19］，因此，在一定范围内BL将更有利于污染物扩散。

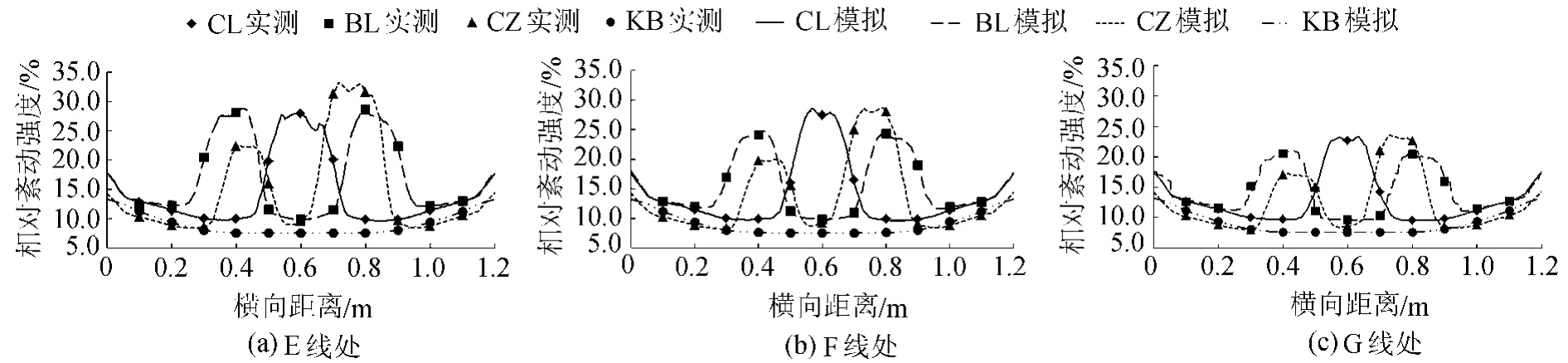
图5 E线、F线和G线处的相对紊动强度分布Fig.5 Relative turbulence intensity distributions of lines E，F，and G

4 结 论

a.除双浮床并列布置外，有无浮床对各断面平均流速影响不大;相对而言，浮床对下游的影响比上游大。

b.3种浮床布置形式在水平面H处及下游的流速分布与无浮床布置情况的流速分布比较，表明:双浮床错开布置对水平面H平均流速、影响范围及下游平均流速影响最大;双浮床并列布置对水平面H影响范围最小;双浮床串列布置对水平面H处及下游的平均流速影响最小。

c.双浮床3种布置形式在水平面H处及下游对平均相对紊动强度影响最大的是并列布置情况，而串列布置与错开布置情况在下游平均相对紊动强度数值相差不大。3种布置形式中，双浮床并列布置更有利于一定范围内的污染物扩散。

［1］郑志宏，魏明华.基于熵值法的改进集对分析水质模拟评价［J］.河海大学学报:自然科学版，2012，41(2):136-139.(ZHENGZhihong，WEI Minghua.Water quality fuzzy evaluation based on entropy method-improved set pair analysis［J］.Journal of Hohai Unversity:Natural Sciences，2013，41(2):136-139.(in Chinese))

［2］HUAI Wenxin，WU Zhenlei，QIAN Zhongdong，et al.Large eddy simulation of open channel flows with non-submerged vegetation［J］.Journal of Hydrodynamics，2011，23(2):258-264.

［3］WANG Peifang，WANG Chao.Numercial model for flow through submerged vegetation regions in a shallow lake［J］.Journal of Hydrodynamics，2011，23(2):170-178.

［4］朱红钧，赵振兴.生态河道种植圈对水流水力特性的影响［J］.水利水运工程学报，2007，1(3):31-35.(ZHU Hongjun，ZHAO Zhenxing.Influences of cropping loops in ecological river on hydraulic behavior of flow［J］.Hydro-science and Engineering，2007，1(3):31-35.(in Chinese))

［5］ATAL B H，ARNAB R.Numerical investigation of low Reynolds number flow past two and three circular cylinders using unstructured grid CFR scheme［J］.International Journal of Heat and Fluid Flow，2010，31(2):154-171.

［6］SUMMER D，PRICE SJ，PAIDOUSSISM P.Flow-pattern identification for two staggered circular cylinders in cross-flow［J］.Journal of Fluid Mechanics，2000，411:263-303.

［7］盛奇伟.并列放置双方柱绕流问题的大涡模拟研究［D］.同济大学，2007:62.

［8］HU Mianhao，YUAN Judong，YANG Xiaoe，et al.Effects of temperature on purification of eutrophic water by floating eco-island system［J］.Acta Ecologica Sinica，2010，30(6):310-318.

［9］魏瑞霞，武会强，张锦瑞，等.植物浮床-微生物对污染水体的修复作用［J］.生态环境学报，2009，18(1):68-74.(WEIRuixia，WU Huiqiang，ZHANG Jinrui，et al.Remediation effects of plant floating bed-microorganism on contaminated water［J］.Ecology and Environmental Sciences，2009，18(1):68-74.(in Chinese))

［10］ZHAO Fengliang，XI Shu，YANG Xiaoe，et al.Purifying eutrophic river waters with integrated floating island systems［J］.Ecological Engineering，2012，40:53-60.

［11］HU Guangji，ZHOU Min，HOU Haibo，et al.An ecological floating-bed made from dredged lake sludge for purification of eutrophic water［J］.Ecological Engineering，2010，36:1448-1458.

［12］马克星，吴海卿，朱东海，等.生物浮床技术研究进展评述［J］.农业环境与发展，2011，28(2):60-64.(MA Kexing，WU Haiqing，ZHU Donghai，et al.Review on the research progress of biological floating bed technology［J］.Agro-Environment and Development，2011，28(2):60-64.(in Chinese))

［13］穆维贤，赖国璋.方柱和双方柱绕流的数值模拟［J］.水动力学研究与进展，1990，5(4):76-80.(MU Weixian，LAI Guozhang.Numerical simulation of fluid flow around a single square-cylinder and a couple of square-cylinders［J］.Journal of Hydrodynamics，1990，5(4):76-80.

［14］饶勇，倪玉山，刘超峰.并列双方柱绕流的Lattice Boltzmann模拟分析［J］.应用力学学报，2008，25(2):192-198.(RAO Yong，NI Yushan，LIU Chaofeng.Lattice Boltzmann simulation of flow around two parallelized square cylinders［J］.Chinese Journal of Applied Mechanics，2008，25(2):192-198.(in Chinese))

［15］胡卫华.基于Fluent的多圆柱体绕流场数值模拟［J］.科技导报，2010，28(24):75-78.(HU Weihua.Simulation of flow around multi-circular-cylinders based on fluent［J］.Scinence and Technology Review，2010，28(24):75-78.(in Chinese))

［16］王远成，吴文权.方柱绕流流场的RNG方法模拟研究［J］.水动力学研究与进展，2004，19(增刊1):916-920.(WANG Yuancheng，WU Wengquan.Numerical simulation of flow around square cylinder using RNG k－ε turbulence model［J］.Journal of Hydrodynamics，2004，19(Sup1):916-920.(in Chinese))

［17］杨纪伟，滕丽娟，郑薇薇，等.用FLUENT模拟不同排列下的双柱绕流流场［J］.人民黄河，2009，31(3):74-75.(YANG Jiwei，TENG Lijuan，ZHENG Weiwei，et al.Simulating flow field under different arrangements of two cylinders based on fluent［J］.Yellow River，2009，31(3):74-75.(in Chinese))

［18］蒲迅赤，李克锋，李嘉，等.紊动随水体中有机物降解影响的实验［J］.中国环境科学，1999，19(6):485-489.(PU Xunchi，LI Kefeng，LI Jia，et al.The effect of turbulence in water body on organic compound biodegradation［J］.China Environmental Science，1999，19(6):485-489.(in Chinese))

［19］王美敬，罗麟，程香菊，等.紊动对有机物降解影响研究［J］.武汉大学学报:工学版，2005，38(4):1-4.(WANG Meijing，LUO Lin，CHRNG Xiangju，et al.Study of effect of turbulence on organic compound biodegradation［J］.Engineering Journal of Wuhan University，2005，38(4):1-4.(in Chinese))