计及负荷静态特性的电力系统静态状态估计算法

陆子刚，卫志农，孙国强，孙永辉，孙维真，王 超

(1.河海大学可再生能源发电技术教育部工程研究中心，江苏南京 210098;2.浙江省电力公司，浙江杭州 310000)

电力系统状态估计的作用是将调度中心接受的精度较低并且偶尔包含不良数据的“生数据”处理成为能够更好地逼近真实值的数据［1-3］，使调度中心对电力系统运行的安全性和经济性能够进行正确的分析和判断，使调度员能够全面掌握电力系统过去、当前、甚至未来的状态［4-5］。

现阶段绝大多数的状态估计常用的算法主要是加权最小二乘算法(weighted least squares，WLS)［6-8］，包括正交化分解法［9］、改进 Givens法［10］和二乘 Givens变换法［11］、基于零注入等式约束的法方程(normal equations with constraints，NE/C)修正牛顿法［12］以及带不等式约束的优化法［13-14］。现代电力系统中负荷模型辨识工作已经深入开展［15］，然而上述方法并未考虑负荷模型对状态估计的影响，仅仅将负荷功率作为节点注入功率参与迭代，忽略了负荷静态特性的作用。随着负荷建模的广泛应用，在常规状态估计中精确计及负荷静态特性的影响已经成为可能，并且是十分有必要的。

笔者在常规WLS状态估计研究的基础上，研究了计及负荷静态特性的电力系统状态估计方法，根据典型负荷静态特性，在所要研究的节点上，利用已经辨识的负荷静态模型替代传统的节点注入功率，将负荷有功、无功功率表示为随电压缓慢变化而变化的等效模型，并构建新的零注入功率量测，负荷静态模型采用幂函数或二次多项式模型，最后利用WLS进行状态估计。利用算例仿真进行分析验证，表明此方法得到的状态估计量精度更高。

1 负荷静态模型

负荷静态模型［16］反映了负荷功率随频率和电压缓慢变化而变化的规律，可用代数方程或曲线表示，其中包括负荷电压特性和负荷频率特性。在稳态运行情况下，电力系统处于缓慢的负荷波动过程中，频率影响可以忽略，因此，只计及负荷电压特性而忽略频率特性时，负荷静态模型用幂函数表示为

式中:PL0、QL0、UL0——在基准点稳态运行时负荷有功功率、无功功率、负荷母线电压幅值;PL、QL、UL——PL0、QL0、UL0的实际值;pU、qU——负荷有功和无功功率的电压特性指数。

负荷静态模型用多项式表示为

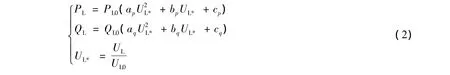
式中:ap、bp、cp——恒定阻抗、恒定电流、恒定功率负荷的有功功率占总有功功率的百分比，且有ap+bp+cp=1;aq、bq、cq——恒定阻抗、恒定电流、恒定功率负荷的无功功率占总无功功率的百分比，且有aq+bq+cq=1。

2 加权最小二乘估计

状态估计的目的是基于量测数据确定系统相对应的最合适状态，电力系统状态估计器采用的估计准则大多是极大似然估计(maximum likelihood estimation，MLE)。

电力系统量测误差通常假定为正态分布:

式中:z——量测随机变量;μ——均值(数学期望)，μ =E(z);σ——z的标准差。

m个不相关且有相同概率密度分布的随机变量的联合概率密度函数为

式中:zi——第 i个量测量;fm(z)——z的似然函数，z=(z1，z2，…，zm)。

极大似然估计通过估计联合密度函数中的给定参数，即均值μ和标准差σ，以达到使似然函数最小的目的。取对数似然方程可得

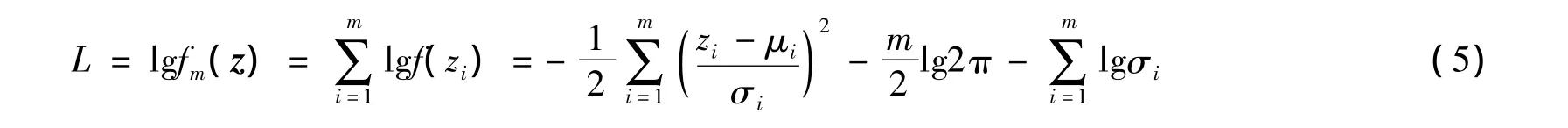
MLE使似然函数对于一组特定的观测值z1，z2，…，zm达到最小，即

定义第i个量测的残差ri为

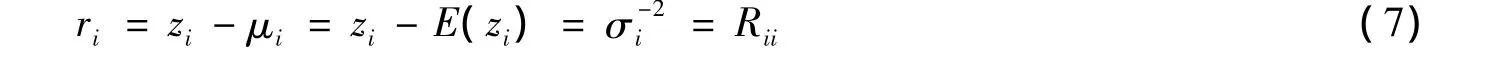
式中均值μi(量测zi的数学期望E(zi))表示为非线性函数hi(x)，hi(x)为状态量x的非线性函数，满足基尔霍夫定律及功率方程等电路基本定理。因此，式(6)等同于对于状态量x求得残差平方加权和的最小值:

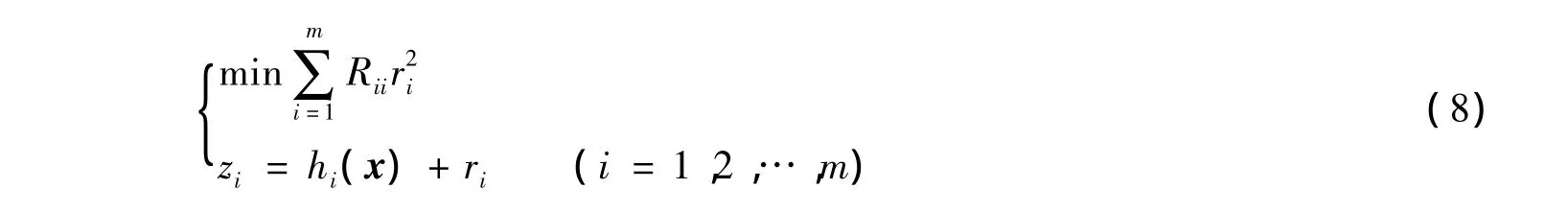
上述最优化问题解法称为对于x的加权最小二乘估计法。

3 计及负荷静态特性的WLS状态估计

在电力系统状态估计中，对于负荷节点，传统的处理方法是将负荷功率量测合并转化为节点注入功率量测，却忽略了负荷自身特性，对负荷功率及系统状态量的估计都会生产偏差。现代电力系统中，负荷模型辨识已日趋完善和精确［17］，下面以单一负荷类型节点为例说明。

传统节点注入功率表示为

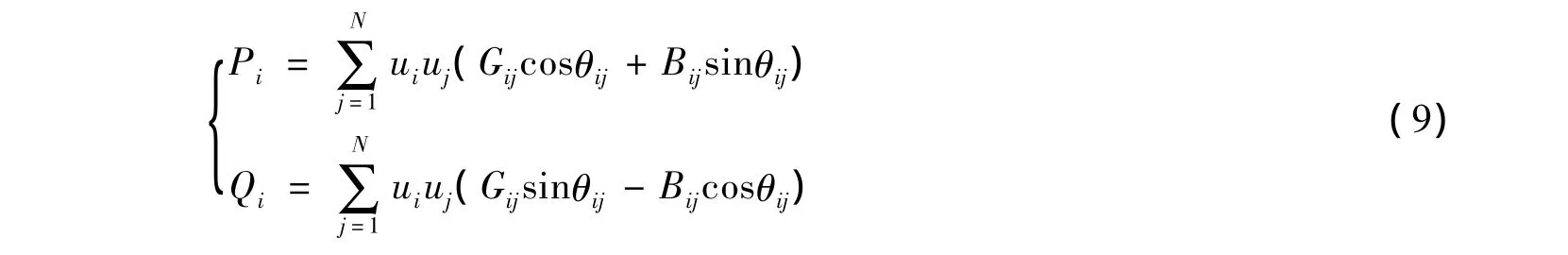
式中:Pi、Qi——节点 i有功、无功注入功率，其方向规定流入节点 i为正，流出节点 i为负;ui、uj——节点 ii、j的电压幅值;θij——节点i到节点j的电压相角差;Gij、Bij——节点导纳阵中对应节点i和j之间的自导纳(互导纳)的电导和电纳;N——网络节点总数。

计及负荷静态特性时，负荷节点采用式(1)(2)两类模型，构建本节点零注入功率，此类负荷节点零注入功率采用幂函数模型和多项式模型表达分别为

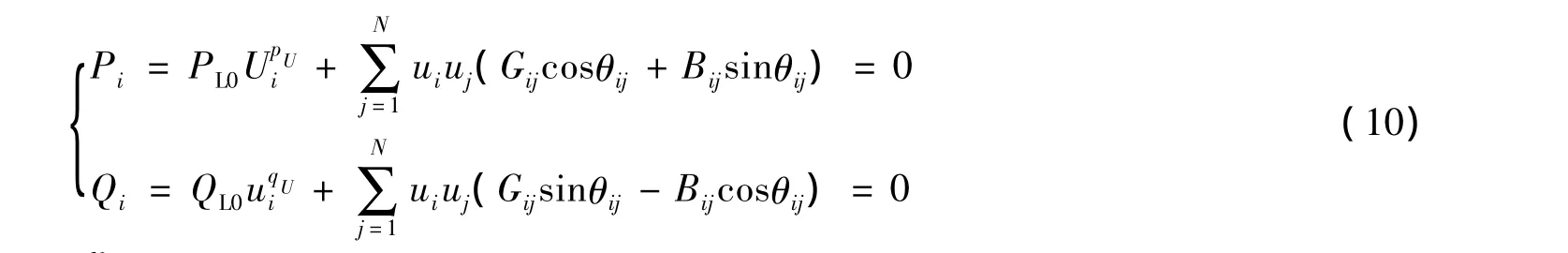
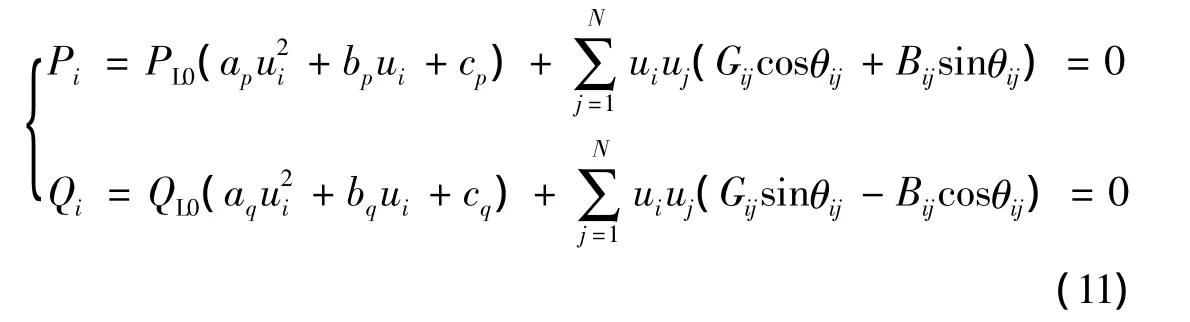
雅克比矩阵H中负荷节点零注入功率Pi、Qi对本节点电压幅值u的偏导增加幂函数或多项式部分求导一项，雅克比矩阵其余各元素不变，幂函数模型和多项式模型中变化的元素分别为

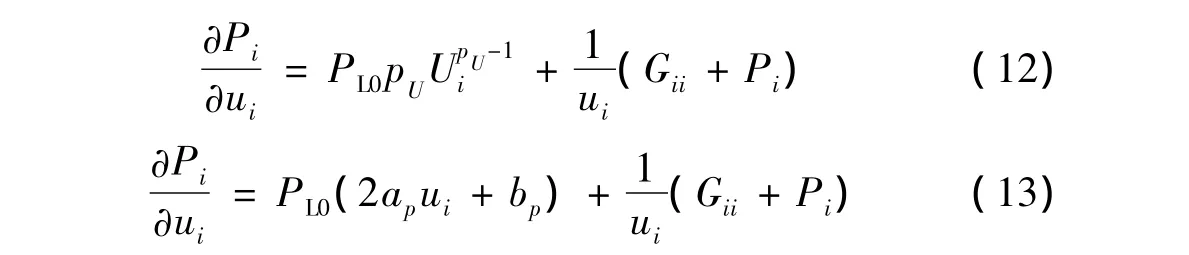
对负荷节点增加的零注入功率量测赋最高权值，等同于伪量测中精确的零注入功率量测。算法的程序流程如图1所示。

4 算例仿真

4.1 节点系统

本文对文献［3］中的4节点标准算例进行了仿真计算，将节点3作为建立负荷静态特性模型的节点，负荷功率采用幂函数模型时为 PL0=48，pU=1.8，QL0=38，qU=2.2，标准差设为10－5;采用多项式模型时为 PL0=48，ap=0.65，bp=0.45，cp= －0.1，QL0=38，aq=0.86，bq=0.5，cq= －0.36，仿真结果见表1。表1给出了在4节点系统中采用幂函数和多项式模型WLS的状态估计量与传统WLS的状态估计量的比较。结果表明，前者的1、2、3节点电压幅值估计量均更接近真值，节点4的电压幅值和相角估计量和后者基本一致。幂函数模型WLS和多项式模型WLS计结果一致，表明在小系统中对于负荷模型及参数变化的影响不明显。总体而言，计及负荷静态特性的状态估计结果更加精确。

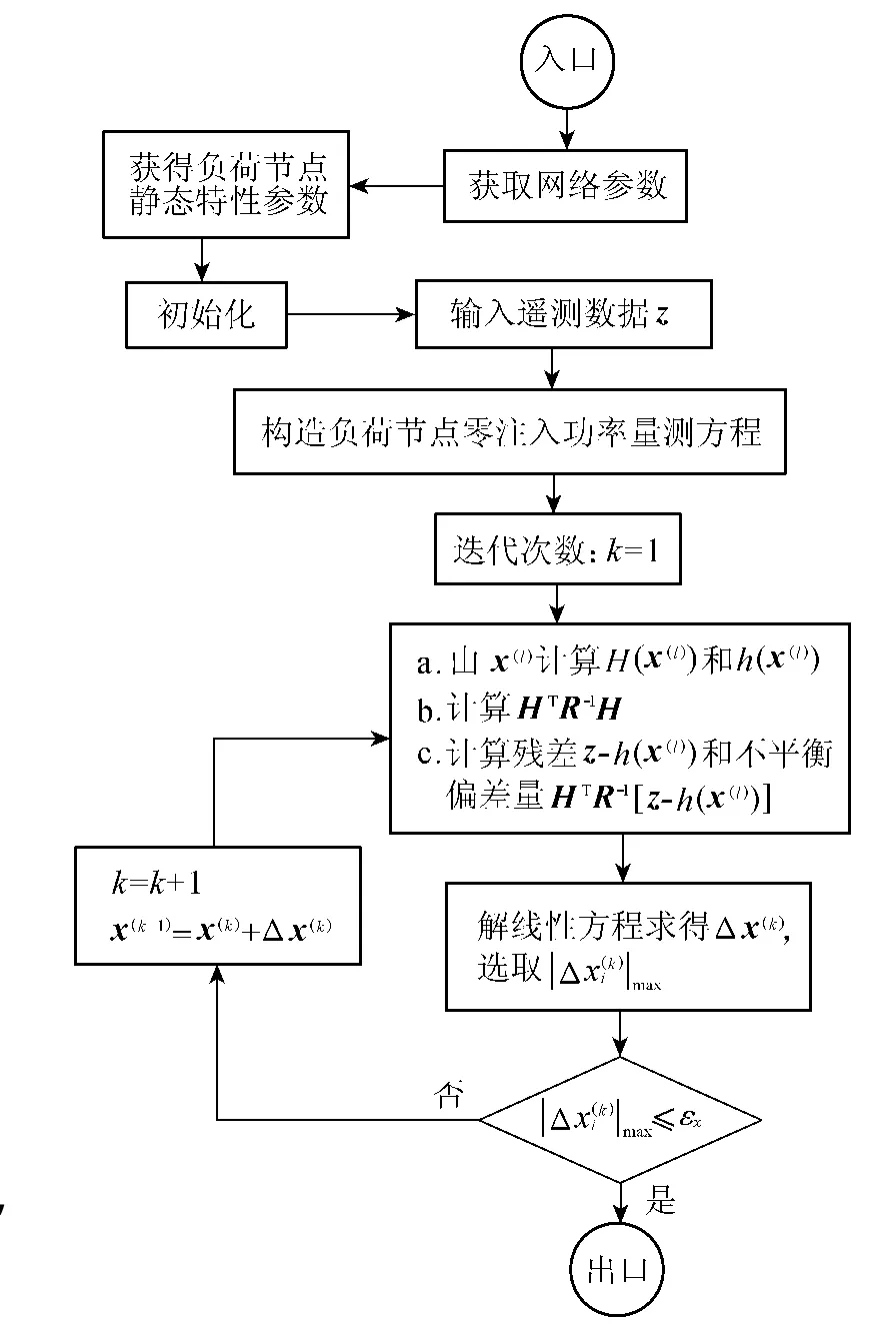
图1 计及负荷静态特性的WLS状态估计算法程序Fig.1 Flowchart of WLS state estimation algorithm considering static characteristics of load

表1 4节点算例仿真结果比较Table 1 Comparison of simulation results of 4-bus system

在4节点系统仿真实验中，常规WLS、幂函数模型WLS和多项式模型WLS的收敛次数都是3次。因此，在小系统中计及负荷静态特性对状态估计迭代计算速度影响不明显。

4.2 IEEE-39节点系统

对IEEE－39节点的标准算例进行仿真计算，结果见表2，其中量测数据是在测试系统潮流结果的基础上叠加相应的正态分布的随机量测误差所产生的。将节点4、8、12、24、26作为建立负荷静态模型的节点，系统如图2所示。

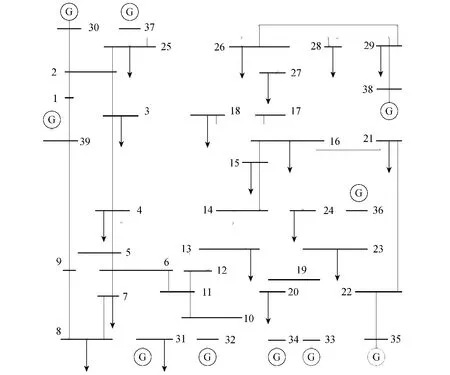
图2 IEEE-39节点系统Fig.2 IEEE 39-bus system

表2给出了在IEEE－39节点系统中计及负荷静态特性的状态估计量结果与常规WLS状态估计量结果的比对。从表2可以看出，虽然节点3、6、17、22、35的幂函数WLS和多项式模型WLS估计量误差稍高于常规WLS估计误差，但误差绝对值基本都在0.1以内，精度完全可以接受，并且其余若干节点的估计误差在幂函数和多项式模型WLS估计中都大幅度减少。在相角估计中，除了节点8、32的相角估计误差在幂函数模型WLS估计中相对未明显降低外，其余各节点的相角估计量误差都有明显降低抑或误差绝对值满足精度要求。总体而言，计及负荷静态特性的两类计算结果都分别或者全部优于常规量测下的计算结果。目标函数J的值在后两次计算中有所下降，此算例中，3次估计的目标函数值分别为151.8843、141.4307和134.7086，自由度K=146，因此，采用幂函数模型WLS和多项式模型WLS的估计结果都符合最优分布。

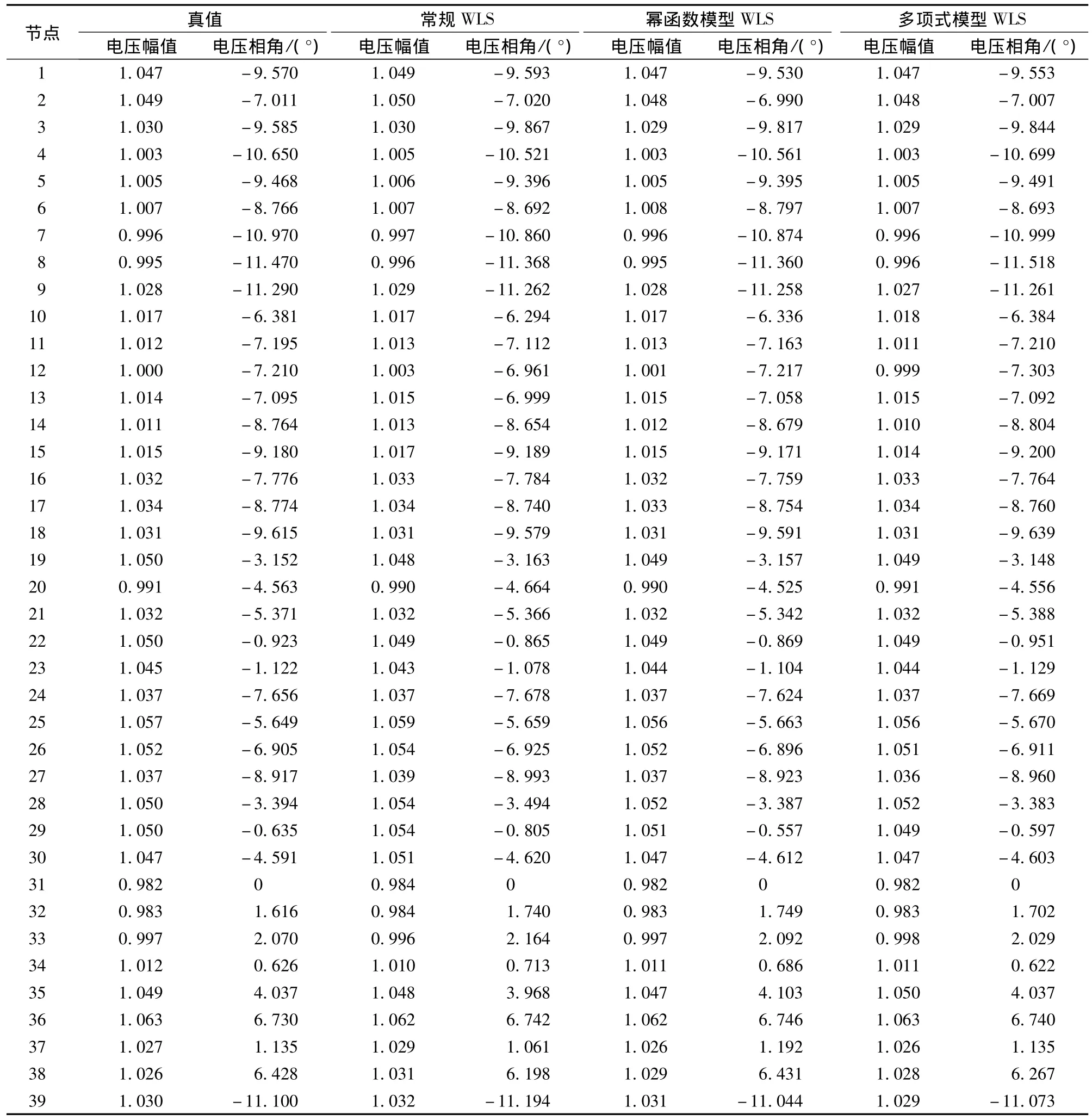
表2 IEEE-39节点算例仿真结果比较Table 2 Comparison of simulation results of IEEE 39-bus system

在IEEE－39节点系统仿真实验中，常规WLS、幂函数模型WLS和多项式模型WLS的收敛次数均为3次。由于仅有5个节点利用了负荷静态模型，因此，迭代计算速度未受到太大影响，收敛次数较常规计算并未有增多。

4.3 实际地区电网算例

采用我国某省网部分地区子网系统作为实际算例进行仿真分析，电网包含233条实际母线，10台降压变压器，907个量测，计算时合并为74个230 kV节点，12个525 kV节点。选取2012年3月1日10:00—12:00的连续断面数据中的10个基本不含不良数据的量测断面进行仿真分析。负荷静态模型采用已辨识的多项式模型，PL0、QL0分别取1，其余参数如表3所示，仿真结果见表4。

表4给出了考虑多项式模型后10个断面的状态估计合格率，此算例中采用了负荷的多项式模型。相比常规WLS，计及负荷静态特性多项式模型WLS的状态估计合格率在每个断面都略有提高，表明了算法的优越性。

仿真实验中，4节点系统、IEEE－39节点系统及实际系统计算都表明，部分节点采用负荷静态特性模型计算时，估计精度皆有所提高，同时提高了实际系统的状态估计合格率，这是由于负荷静态模型参数的辨识具有统计规律。由于仅考虑了静态特性，并未涉及动态特性，因此，实际计算中每个断面的状态估计合格率都提高了0.2%左右。同时，系统运行时节点电压幅值变化不大，在计及负荷静态特性的状态估计时，估计精度都满足运行工况的要求。

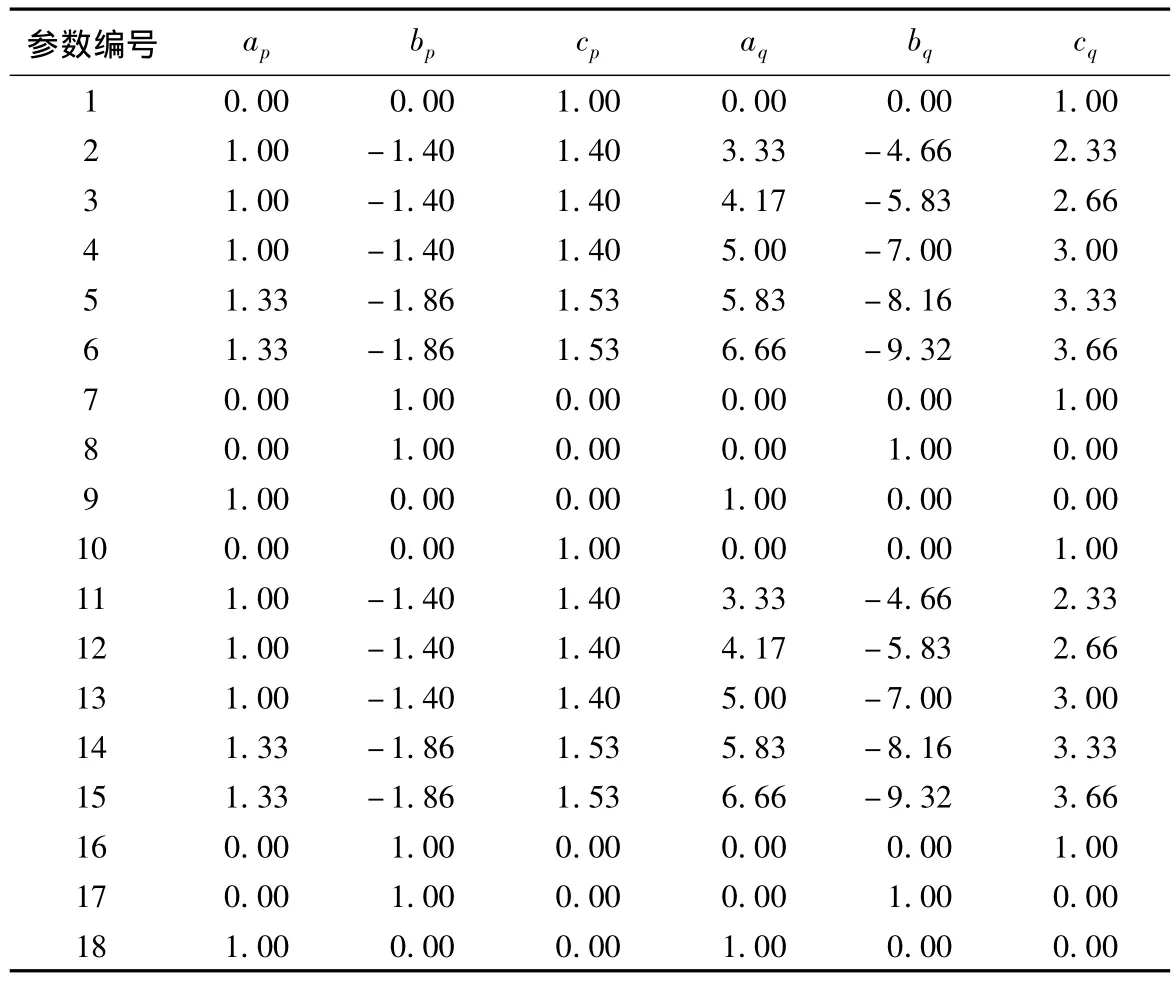
表3 负荷静态模型参数Table 3 Parameters of static load model

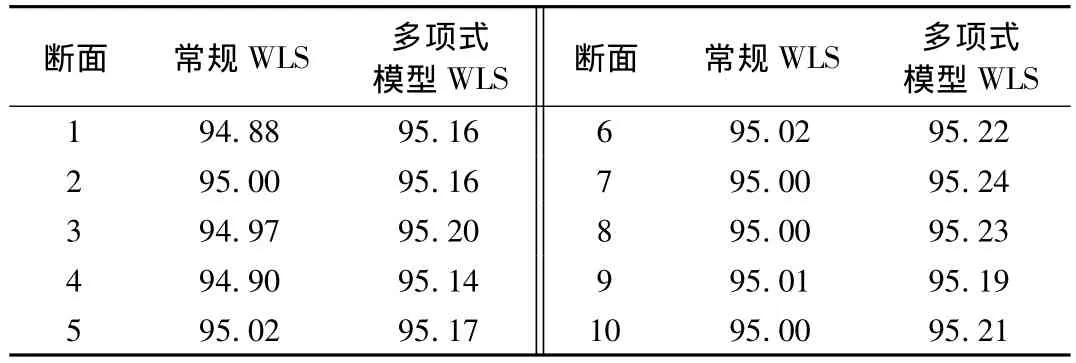
表4 实际地区电网算例10个断面状态估计合格率对比Table 4 Comparison of state estimation acceptance rates for ten snap shots in regional network

5 结 语

在电力系统常规量测的基础上，利用负荷静态电压特性，在特定节点上建立了基于负荷静态特性的幂函数模型和多项式模型。利用零注入功率量测构建精确的伪量测量，补充并提高了量测系统的完整性和精确性，做加权最小二乘静态状态估计，有效地提高了状态估计量精度，更有利于提升电力系统高级分析软件结果的可信度，具有较好的实用性。

［1］EXPOSITO A G，JAEN A V.Two-level state estimation with local measurement pre-processing［J］.IEEE Transactions on Power Systems，2009，24(2):676-684.

［2］VANFRETTI L，CHOW J H，SARAWGI S，et al.A phasor-data-based state estimator incorporating phasor bias correction［J］.IEEE Transactions on Power Systems，2011，26(1):111-119.

［3］JABR R A，PAL B C.AC network state estimation using linear measurement functions［J］.IET Proceedings-Generation Transmission and Distribution，2008，2(1):1-6.

［4］庞博，卫志农，孙国强.基于风力发电机简化RX模型的电力系统状态估计［J］.电网技术，2009，33(19):159-163.(PANG Bo，WEI Zhinong，SUN Guoqiang.Power system state estimation based on simplified RX model of wind power generator［J］.Power System Technology，2009，33(19):159-163.(in Chinese))

［5］姚诸香，郭烨，郭玉金，等.含指数型目标函数的电力系统抗差状态估计方法在江西电网中的应用［J］.电网技术，2012，36(4):155-159.(YAOZhuxiang，GUOYe，GUOYujin，et al.Application of a robust state estimator based on maximum exponential square in Jiangxi power system［J］.Power System Technology，2012，36(4):155-159.(in Chinese))

［6］王勇，郭志忠，彭茂君，等.基于分解协调算法的互联电力系统状态估计［J］.电网技术，2008，32(10):79-83.(WANG Yong，GUO Zhizhong，PENG Maojun，et al.A new decomposition and coordination algorithm for state estimation in interconnected power system［J］.Power System Technology，2008，32(10):79-83.(in Chinese))

［7］宁辽逸，孙宏斌，吴文传.基于状态估计的电网支路参数估计方法［J］.中国电机工程学报，2009，29(1):7-13.(NING Liaoyi，SUN Hongbin，WU Wenchuan，et al.State estimation based on branch parameter estimation method for power grid［J］.Proceedings of the CSEE，2009，29(1):7-13.(in Chinese))

［8］卢志刚，程慧琳，冯磊，等.基于证据融合理论的多不良数据辨识［J］.电网技术，2012，36(1):123-128.(LU Zhigang，CHENG Huilin，FENG Lei，et al.Multi bad data identification based on evidence fusion theory［J］.Power System Technology，2012，36(1):123-128.(in Chinese))

［9］KILOKYS E，SINGH N.Minimum correction method for enforcing limits and equality constraints in state estimation based on orthogonal transformations［J］.IEEE Transactions on Power Systems，2000，15(4):1281-1286.

［10］郭瑞鹏，邵学检，韩祯祥.基于分块吉文斯旋转的电力系统状态估计［J］.中国电机工程学报，2006，26(12):26-31.(GUO Ruipeng，SHAO Xuejian，HAN Zhenxiang.A blocked Givens rotations based algorithm for power system state estimation［J］.Proceedings of the CSEE，2006，26(12):26-31.(in Chinese))

［11］鲍海波，韦化.考虑风电的电压稳定概率评估的随机响应面法［J］.中国电机工程学报，2012，32(13):77-85.(BAO Haibo，WEI Hua.A stochastic response surface method for probabilistic evaluation of the voltage stability considering wind power［J］.Proceedings of the CSEE，2012，32(13):77-85.(in Chinese))

［12］郭烨，张伯明，吴文传，等.直角坐标下含零注入约束的电力系统状态估计修正牛顿法［J］.中国电机工程学报，2012，32(19):96-100.(GUO Ye，ZHANG Boming，WU Wenchuan，et al.Power system state estimation solution with zero injection constraints using modified Newton method［J］.Proceedings of the CSEE，2012，32(19):96-100.(in Chinese))

［13］王勇，郭志忠，彭茂君，等.基于分解协调算法的互联电力系统状态估计［J］.电网技术，2008，32(10):79-83.(WANG Yong，GUO Zhizhong，PENG Maojun，et al.A new decomposition and coordination algorithm for state estimation in interconnected power system［J］.Power System Technology，2008，32(10):79-83.(in Chinese))

［14］赵渊，杨晓嵩，谢开贵.UPFC对电网可靠性的灵敏度分析及优化配置［J］.电力系统自动化，2012，36(1):55-59.(ZHAO Yuan，YANG Xiaosong，XIE Kaigui.Parameter sensitivity and optimal allocation of UPFCs in bulk power systems reliability assessment［J］.Automation of Electric Power Systems，2012，36(1):55-59.(in Chinese))

［15］鞠平.电力系统建模理论与方法［M］.北京:科学出版社，2010:244-289.

［16］马进，贺仁睦，王景钢，等.综合负荷模型参数的简化辨识策略［J］.电网技术，2006，30(9):28-34.(MA Jin，HE Renmu，WANG Jinggang.Simplified identification strategy for composite load model parameters［J］.Power System Technology，2006，30(9):28-34.(in Chinese))

［17］倪以信，陈寿孙，张宝霖.动态电力系统的理论和分析［M］.北京:清华大学出版社，2002:81-82.