软土地区隧道管片受力与变形研究

黎春林

(1.铜陵学院土木建筑系，安徽 铜陵 244000;2.东南大学岩土工程研究所，江苏南京 210096)

建设在软土中的隧道，因土体具有流变性能，其应力和应变随时间不断变化，不但会引起土体的长期沉降［1-4］，而且会增加隧道衬砌的受力和变形，对地铁隧道安全和结构防水性以及耐久性等构成威胁［5］。针对隧道施工中衬砌的受力和变形，国内外学者已做了许多研究。文献［6］根据圆形隧洞的二维弹性解，研究了围岩特征曲线与支护反力曲线的关系，但因是弹性解，无法准确描述围岩的屈服破坏及围岩变形的时间效应。文献［7］应用弹塑性理论，研究了围岩与支护的相互作用，围岩的屈服过程通过残留强度的逐渐减小来描述，但并没有考虑时间效应。近年来，将应用于边坡工程的强度折减方法引入到地下工程的围岩稳定性分析已成为热点［8］，但该方法也仅考虑了围岩力学参数的劣化而没有考虑其流变性能。文献［9-10］根据线性黏弹性模型，应用Kelvin模型或Maxwell模型对弹性支护情况下的隧洞围岩变形进行了解析，分析了隧洞洞周位移随时间的变化，但没有考虑围岩的屈服破坏现象。文献［11-14］应用非线性黏弹性模型，采用数值方法对围岩的变形特性及衬砌受力进行了分析，但岩土工程的复杂性决定了数值方法结果与工程实际存在一定误差。文献［15］通过对隧道围岩蠕变特性衬砌变形的理论公式的分析，利用现场实测数据拟合公式，确定了围岩的流变参数，并给出衬砌合理的支护时机，但因现场试验影响因素复杂，与蠕变无关的因素对变形结果的影响难以厘清，流变参数的准确性难以得到保证。

笔者根据原状土体的室内三轴蠕变试验数据，采用最小二乘法拟合蠕变方程，获取蠕变参数，并将蠕变方程与小孔扩张理论相结合，推导出可以表征时间因素的围岩特征曲线方程解析解，给出求解隧道周边变形和支护力随时间变化的一种简便实用的方法，并应用于无锡地铁1号线工程实例中。

1 蠕变本构方程的建立

研究盾构隧道工程中周边土体的变形，一种较适用的方法是进行能够模拟土体实际应力路径的三轴蠕变试验。针对土体的流变特性，很多学者根据岩石的应力-应变曲线特点，构建了土体的蠕变模型，如Maxwell模型、Bingham模型、Kelvin模型、西原模型等［16］。结合Bingham模型和Kelvin模型，可以构建能完整地描述土体的蠕变衰减阶段、稳态蠕变阶段和加速蠕变阶段的蠕变本构方程:

其中

式中:ε(t)——蠕变变形;E1——弹性模量;E2——黏性模量;η1、η2——黏弹性系数;σ——主应力差;αs——屈服应力;β——材料参数;t——蠕变经历的时间;t*——稳态蠕变向加速蠕变过渡的时间。

引入符号函数sgn(x)，式(1)可转化为

其中

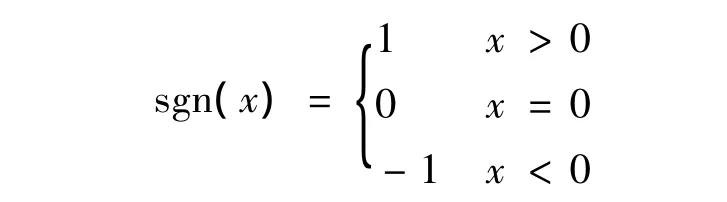
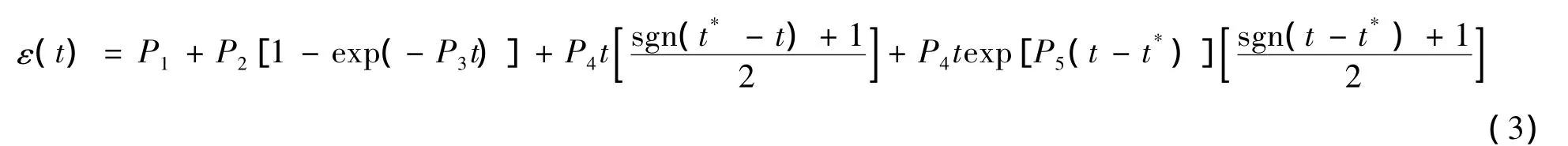
式中:P1、P2、P3、P4、P5——待拟合参数。

2 考虑蠕变的隧道周边地层特征曲线方程

隧道开挖后，围岩内力会重新分布。当隧道的围岩是软土时，内力重分布会引起土体蠕变，并进一步影响管片的最终受力。如果软土的蠕变较大，管片将发生较大的变形，甚至被压溃。基于黏弹塑性理论，结合蠕变方程(3)，分别针对隧道周边土体未发生屈服和发生屈服两种情况，对隧道周边变形和管片的受力进行探讨。

2.1 隧道周边土体未发生屈服

在弹性应力状态下，当隧道周边有衬砌支护力Pa作用时，隧道周边弹性区径向应力σr和切向应力σθ可用式(4)表示［17］:

其中

式中:σ0——初始地应力;a——隧道半径;r——计算点至隧道中心的距离。

隧道开挖时，隧道周边土体径向位移为

式中:μ1——土的泊松比;p0——隧道开挖释放荷载，p0= σ0－Pa。

考虑时间效应后，土体位移是时间的函数，以ur(t)表示，其值为

其中

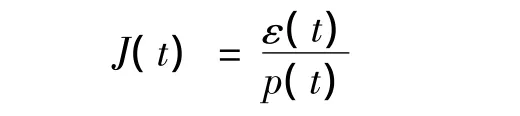
式中:J(t)——蠕变柔量内核;p(t)——某一时刻土层应力释放量。

若忽略应力释放量随时间的变化，即假定p(t)=p0，则式(6)转变为

对于盾构隧道，施工中不容许出现稳态蠕变和加速蠕变阶段，否则隧道将垮塌，因此衰减蠕变是关注重点。如果蠕变只有衰减蠕变阶段，则由式(3)和式(7)可得

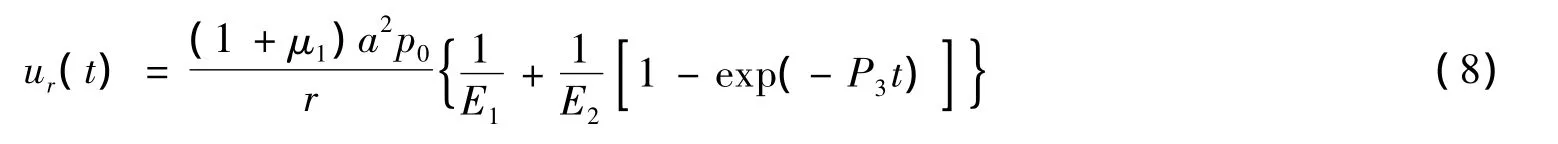
当围压稳定不变时，假定轴向应力增加量Δσ1引起轴向应变的变化量为Δε1，则

同理可得

将式(9)和(10)代入式(8)可得

其中

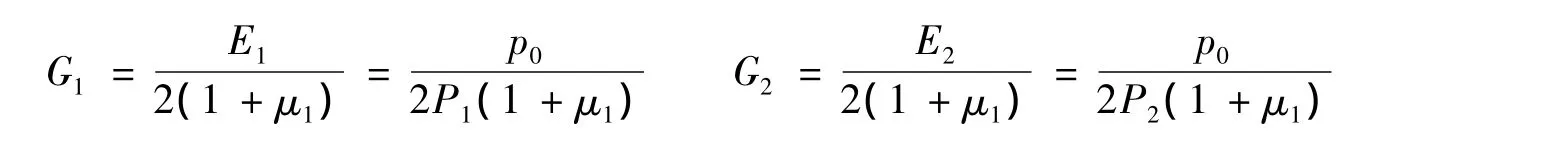
式中:G1——围岩的剪切模量;G2——围岩的蠕变模量。

取r=a，由式(11)得到隧道周边位移

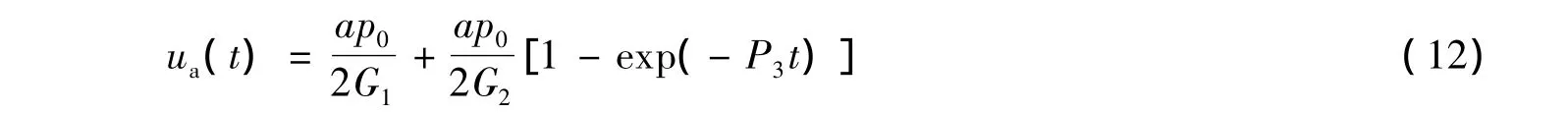
假定p0对应的蠕变参数为P1、P2，将其代入式(12)，则隧道周边土体位移随时间的变化为

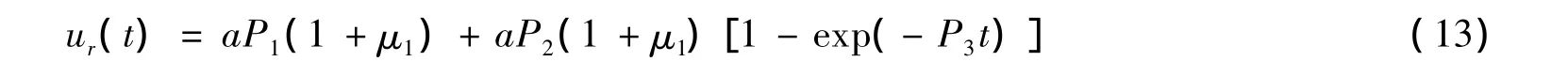
2.2 隧道周边土体发生屈服

隧道周边土体发生屈服时，土体产生的塑性流动属于约束塑性变形，即它的流动量取决于未进入塑性流动的弹性区的蠕变量。因此，控制围岩蠕变的关键是控制围岩中弹性区的蠕变，计算考虑时间效应的塑性区位移，也必须以弹性区的土体蠕变为研究对象。隧道周边土体屈服后，弹性区的径向应力和切向应力可由式(14)表示［18］:

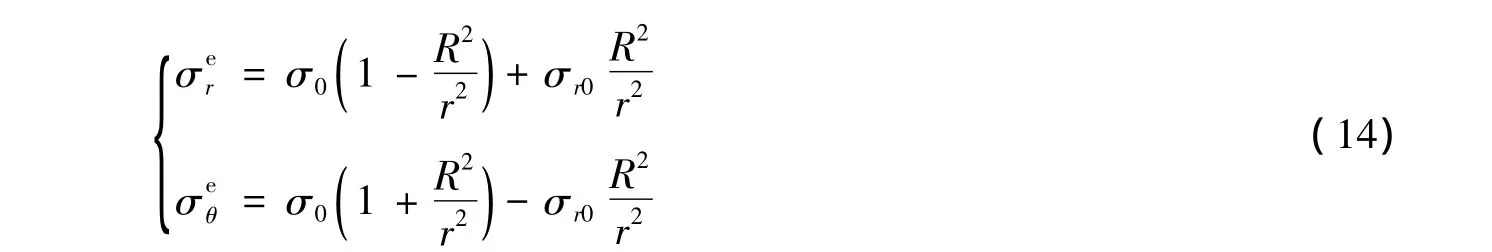
其中

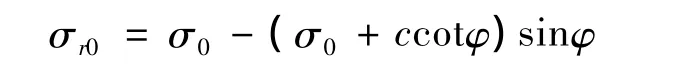
应用摩尔库伦屈服准则，可推导出不考虑土的蠕变时土体塑性区和弹性区径向位移为［19］

考虑土体黏性后，土体径向位移ur(t)随时间的变化为

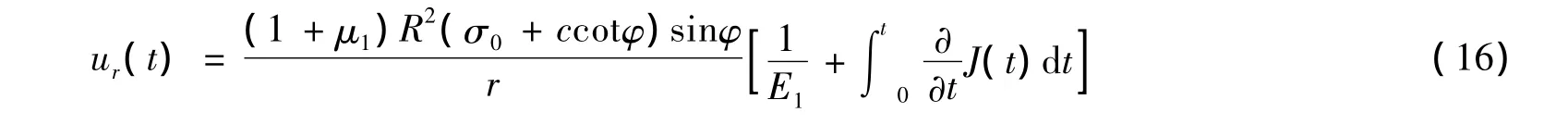
将蠕变方程(3)代入式(16)，如果只考虑衰减蠕变阶段，则任意时刻隧道周边土体的径向位移为

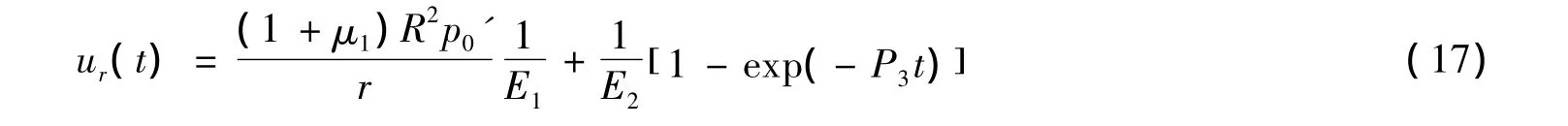
其中

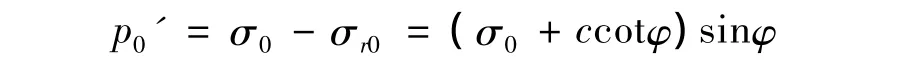
式中:p0'——隧道开挖弹塑性分界面处土层释放荷载。

将式(17)变换成如下形式:

取r=a，由式(18)得到隧道周边的位移

假定弹塑性交界面处土层释放荷载p0'对应的蠕变参数为P1、P2，将其代入式(19)，则隧道周边土体位移随时间的变化为

其中

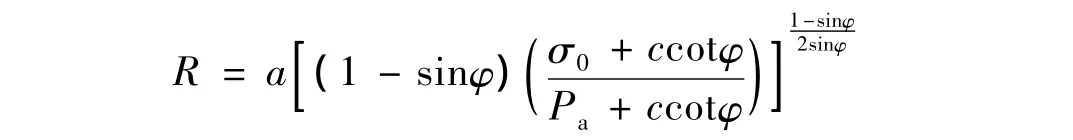
由式(13)和式(20)可知，蠕变参数P1决定了其施工瞬时变形的大小，蠕变参数P2决定了蠕变总的变形大小，而蠕变参数P3决定了蠕变变形随时间的变化速率。

3 工程实例

隧道周边土体位移不但与支护力大小有关，还与时间有关。下面对无锡地铁1号线现场钻取的原状土进行蠕变试验，分析其变形随时间的发展规律，获取蠕变参数，并确定管片受力和变形随时间的变化规律。

3.1 无锡软土蠕变试验结果

土样取自无锡地铁1号线高浪站，取土深度20.1～20.4 m。蠕变时的围压为250 kPa，分级加载，试验开始时每级荷载差值40 kPa，随后每级荷载差值采用20 kPa，土体濒临破坏时每级荷载差值采用12.5 kPa。在第8级荷载(主应力偏差205 kPa)下试样很快进入加速蠕变阶段并破坏。各级荷载作用下的蠕变试验结果如图1所示。

3.2 蠕变试验数据的拟合

如果隧道周边土体未出现屈服，则由式(12)计算得到隧道周边土体位移。如果隧道周边土体发生屈服，根据勘察资料，土体黏聚力c=26.39 kPa，内摩擦角φ=15.49°，土体初始地应力σ0=370 kPa，则弹塑性交界面处隧道开挖前后的应力差值 p0'=(σ0+c cotφ)sinφ =124.25 kPa。

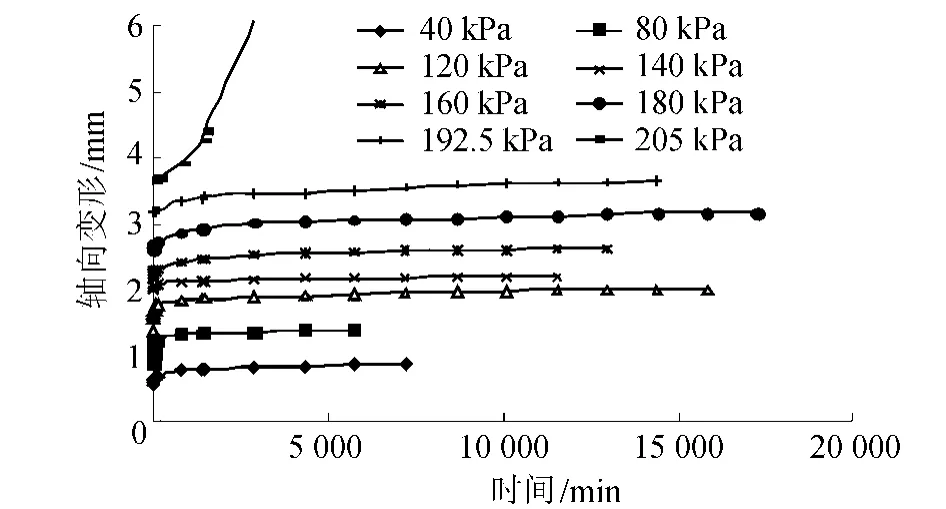
图1 三轴蠕变试验曲线Fig.1 Tested curves of soils under triaxial creep condition

由于隧道开挖，在隧道周边土体内出现了应力释放，在弹塑性交界面处，土体应力的释放量为124.25 kPa。根据前文分析，隧道屈服后应以弹性区为蠕变研究对象。采用Origin软件对试验数据进行拟合，图2是土样三轴蠕变试验在主应力差分别为120 kPa和140 kPa时的拟合结果。

3.3 管片受力和土体变形随时间的变化

在弹塑性交界面处，因为盾构隧道的开挖，土体应力的释放量为124.25 kPa。如图2所示，当主应力差为120 kPa时，土样为衰减蠕变，其蠕变拟合参数P1=0.016 6，P2=0.002 0，P3=0.000 38;当主应力差为140 kPa时，土样也为衰减蠕变，其蠕变拟合参数P1=0.019 7，P2=0.001 2，P3=0.000 36。若主应力差为124.25 kPa，因荷载处于120～140 kPa之间，土样也必为衰减蠕变，其蠕变拟合参数P1、P2和P3可采用线性内插的方法得到:P1=0.0173，P2=0.0018，P3=0.00036。则由式(20)可计算得出隧道周边土体位移，进而得到考虑蠕变的隧道周边土体位移特征曲线。

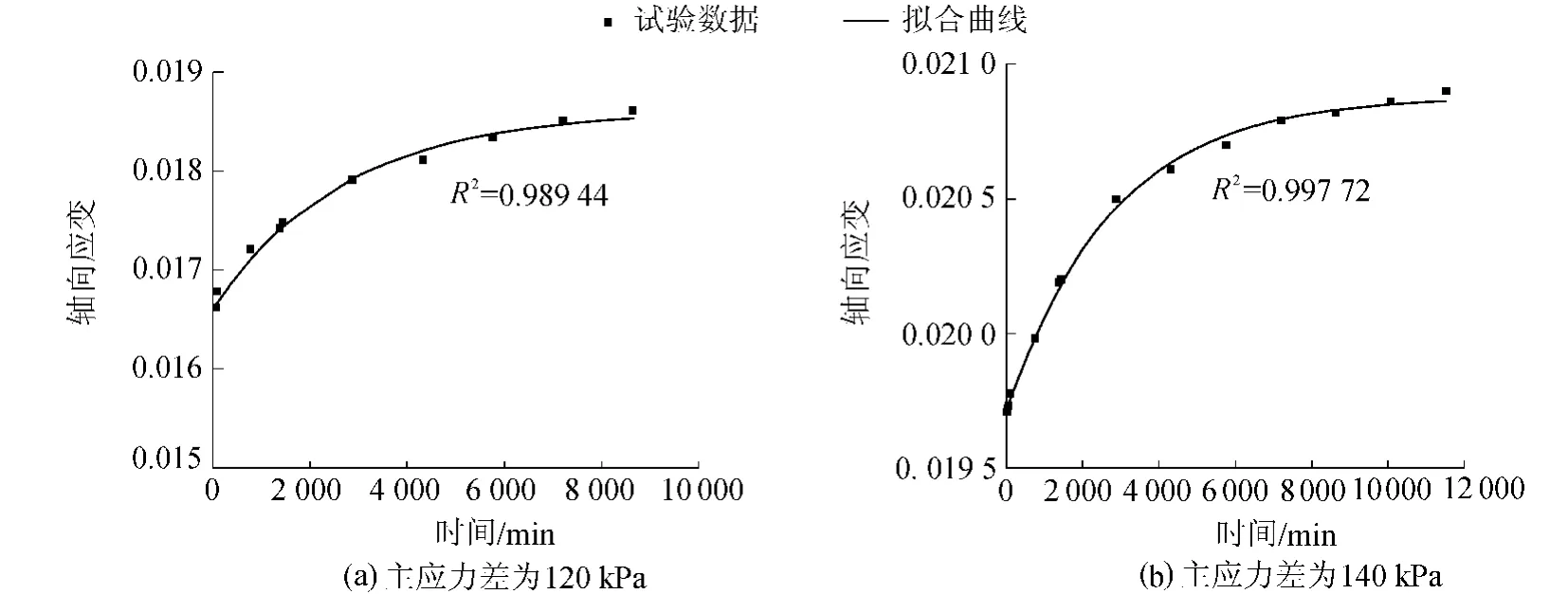
图2 三轴蠕变试验数据和拟合曲线Fig.2 Triaxial creep testing data and fitting curves

假定隧道为瞬时开挖，共计开挖时刻时间点为0，图3分别描述了盾构施工瞬时、施工1 d后、施工1个月后和施工1 a后的土体位移特征曲线。计算结果表明，因土体蠕变，围岩位移特征曲线是以时间为参数的曲线簇，随着时间的增加，曲线向右移动，但不是简单的平移，每点移动的距离不一样，支护力较大时，土体应力释放小，蠕变较小，特征曲线向右移动的距离也较小。

土体蠕变对管片支护力及洞周变形的影响还与管片的刚度有关。图3中A线和B线为支护特征曲线，A线表示管片的刚度较小，随着时间的推移，管片的变形和管片支护力都逐渐增大;B线表示管片刚度很大，隧道周边位移不会随时间发生变化，而管片的支护力因为土体的蠕变随时间延长逐渐增大。假定隧道周边土体位移保持100 mm不变，当管片刚度很大时，管片支护力在开挖支护瞬时为223 kPa，施工1 d后支护力增加至262 kPa，施工1个月后支护力增加至296 kPa，施工1 a后支护力增加至300 kPa。由此可知，随着时间的增加，管片支护力逐渐增加，但增加的速率逐渐减小，管片支护力最终趋向一定值。

3.4 管片刚度对管片受力及变形的影响

对于盾构隧道，支护特征曲线取决于管片的刚度。管片对围岩变形提供一定的约束力，即支护阻力，其大小随支护变形而增加的情况为支护特征曲线，支护特征曲线与管片的刚度有关，如图4所示。

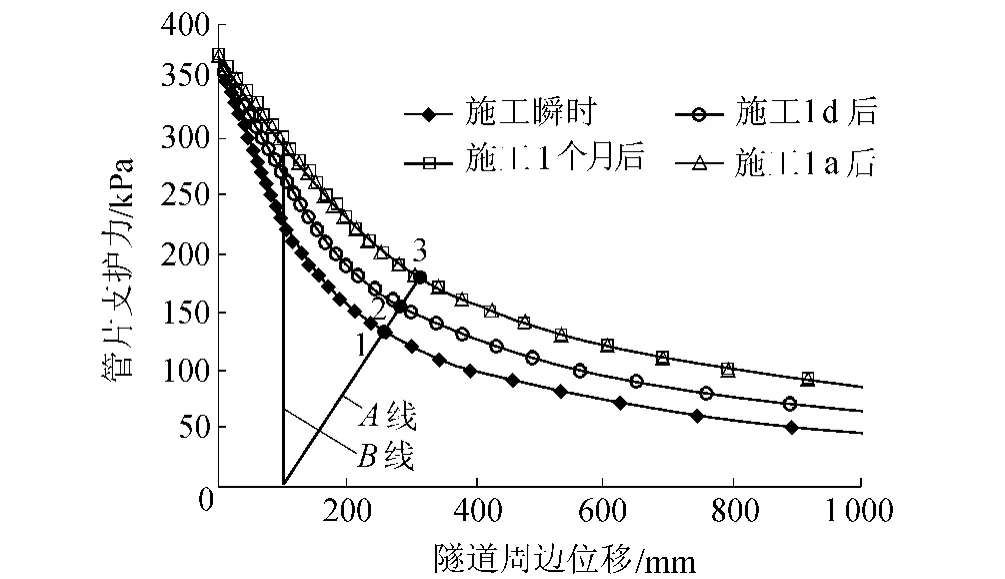
图3 不同施工时间的围岩特征曲线及管片支护力Fig.3 Characteristic curves of surrounding rocks and segment supporting force at different construction times

图4 管片刚度对管片压力的影响Fig.4 Influence of segment stiffness on segment pressure

管片的刚度为支护特征曲线的斜率，管片构成的支护结构的力学特性可以认为是线弹性的，也就是说支护力Pa和它的径向位移ua－u0呈线性关系［20］，即

其中

式中:Ks——管片等效刚度;u0——支护开始发挥作用时隧道洞周径向位移;ua——平衡时隧道洞周径向位移;E0——管片材料的弹性模量;d——管片的厚度;D——隧道的外径。

在土压力作用下围岩和管片发生变形，在变形过程中，围岩因部分变形能释放，其稳定需要的支护力逐渐降低，而管片的支护力随着管片的变形逐渐增长，最终围岩特征曲线和管片支护特征曲线会相交于一点而达到平衡，如图4所示。在围岩特征曲线一定的情况下，支护特征曲线和围岩特征曲线的交点取决于u0和支护特征曲线的斜率。比较图4中直线ba、ba1和ba2，可知柔性管片比刚性管片承受更小的压力，但达到平衡时隧道周边土体需要更大的位移。

如果不考虑时间效应，支护特征曲线和围岩特征曲线的交点唯一，其位置不发生变化，即在周边土体的位移和管片的支护力都是恒定的。考虑土体的蠕变后，如图3中A线所示，随着时间推移，支护特征曲线与围岩特征曲线的交点分别为1点、2点、3点，交点不断向图中右上方移动，即洞周土体位移和管片的支护力都随着时间的增加逐渐增大。下面以无锡地铁盾构隧道为例，具体分析管片支护力随时间的变化规律。无锡盾构隧道外径为6.2 m，管片厚度为0.35 m，管片材料弹性模量为28 GPa。考虑刚度折减和混凝土的流变［17］，文中管片弹性模量采用3.4 GPa，计算得到Ks≈131.2 kPa/mm。

因为管片的刚度很大，可以近似认为支护特征曲线垂直。假定初始位移为100 mm，结合考虑蠕变的隧道周边土体位移特征曲线，可得管片的支护力随时间的变化关系，如图5所示。结果表明，因为土体蠕变，管片支护力逐渐增加，开始时变化迅速，随后逐渐趋于稳定，稳定时的支护力为302 kPa，与上覆土体自重应力370 kPa比较，稳定时管片的支护力约为上覆土体自重应力的82%。

4 结 语

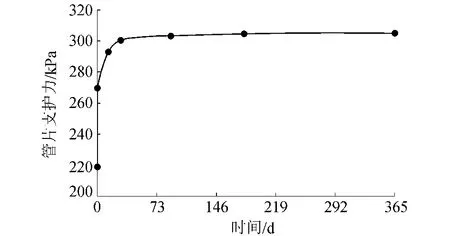
图5 管片支护力-时间曲线Fig.5 Segment supporting force vs.time

通过室内三轴蠕变试验获取蠕变参数，并将蠕变方程与小孔扩张理论相结合，给出了一种可对隧道围岩进行黏弹塑性分析的简便实用的方法，可用于解决隧道周边土体的长期变形和管片受力问题。结合无锡地铁1号线工程，研究了隧道周边变形和支护力随时间的变化规律。研究结果表明，考虑蠕变以后，随着时间的增加，围岩特征曲线向右偏移，曲线变得平缓，这就意味着相同的支护力下会发生更大的变形，而限定某一变形则需要更大的支护力。对于柔性隧道，土体蠕变会引起洞周位移和管片支护力都随着时间增大;对于刚性隧道(如盾构隧道)，因其管片刚度较大，变形受土体蠕变影响较小，其影响主要体现在管片支护力随时间的变化上。

［1］SHIRLAW J N.Observed and calculated pore pressure and deformations induced by an earth balance shield discussion［J］.Canadian Geotechnical Journal，1995，32(1):181-189.

［2］张冬梅，黄宏伟，王箭明.软土隧道地表长期沉降的黏弹性流变与固结耦合分析［J］.岩石力学与工程学报，2003，22(增刊1):2359-2362.(ZHANG Dongmei，HUANG Hongwei，WANG Jianming.Analysis of long-term settlements over tunnels using visco-elastic constitutive model coupled with consolidation theory［J］.Chinese Journal of Rock Mechanics and Engineering，2003，22(Sup1):2359-2362.(in Chinese))

［3］魏纲.盾构施工引起地面长期沉降的理论计算研究［J］.岩石力学与工程学报，2008，27(增刊1):2960-2966.(WEI Gang.Research on theoretical calculation of long-term ground settlement caused by shield tunneling［J］.Chinese Journal of Rock Mechanics and Engineering，2008，27(Sup1):2960-2966.(in Chinese))

［4］璩继立.软土地区盾构施工引起的土地变形研究［D］.上海:同济大学，2005.

［5］KIYAMA H，FUJIMURA H，NISHIMURA T，et al.Theoretical construction of bearing characteristic curve in tunneling［J］.J Soc Mat Sci，1992，41:417-423.

［6］李桂华，黄腾，席广永，等.软土地铁隧道运营期沉降监控研究综述［J］.河海大学学报:自然科学版，2011，39(3):277-284.(LI Guihua，HUANG Teng，XI Guangyoug，et al.Review of researches on settlement monitoring of metro tunnels in soft soil during operation period［J］.Journal of Hohai University:Natural Sciences，2011，39(3):277-284.(in Chinese))

［7］FAIRHURST C，DAEMEN J JK.Practical inferences from research on the design of tunnel supports［J］.Underground Space，1980，4:297-311.

［8］陈国庆，冯夏庭，江权，等.考虑岩体劣化的大型地下厂房围岩变形动态监测预警方法研究［J］.岩土力学，2010，31(9):3012-3018.(CHEN Guoqing，FENG Xiating，JIANG Quan，et al.Study of dynamic early warning method of surrounding rock deformation monitoring for large underground powerhouse considering rock degradation［J］.Rock and Soil Mechanics，2010，31(9):3012-3018.(in Chinese))

［9］PAN Y W，DONG JJ.Time-dependent tunnel convergence-Ⅱ:advance rate and tunnel-support interaction［J］.Int JRock Mech Min Sci Geomech，1991，28:477-488.

［10］LADANYI B，GILL D E.Design of tunnel linings in a creeping rock［J］.Int J Min ＆ Geological Eng，1988，6:113-126.

［11］金丰年.考虑时间效应的围岩特征曲线［J］.岩石力学与工程学报，1997，16(4):344-353.(JIN Fengnian.Time-dependent ground characteristic curves around tunnel［J］.Chinese Journal of Rock Mechanics and Engineering，1997，16(4):344-353.(in Chinese))

［12］齐明山，徐正良，崔勤，等.厦门海底隧道围岩流变特性及其特征曲线［J］.岩土力学，2007，28(增刊1):493-496.(QI Mingshan，XU Zhengliang，CUI Qin，et al.Rheological properties of surrounding rock of Xiamen Subsea Tunnel and its characteristic curve［J］.Rock and Soil Mechanics，2007，28(Sup1):493-496.(in Chinese))

［13］王迎超，尚岳全，孙红月，等.复合式衬砌在围岩蠕变过程中的受力规律研究［J］.水文地质工程地质，2010，37(2):49-54.(WANG Yingchao，SHANG Yuequan，SUN Hongyue，et al.Study on mechanical rules of double-lining in creeping surrounding rock［J］.Hydrogeology and Engineering Geology，2010，37(2):49-54.(in Chinese))

［14］李建军，张志强.岩石蠕变对隧道二次衬砌结构影响的研究［J］.现代隧道技术，2011，48(6):58-64.(LI Jianjun，ZHANG Zhiqiang.Study of the influence of rock creep on the structure of a tunnel’s secondary lining［J］.Modern Tunnelling Technology，2011，48(6):58-64.(in Chinese))

［15］王中文，方建勤，夏才初，等.考虑围岩蠕变特性的隧道二衬合理支护时机确定方法［J］.岩石力学与工程学报，2010，29(增刊 1):3241-3246.(WANG Zhongwen，FANG Jianqin，XIA Caichu，et al.Determination method of supporting time for secondary lining in tunnel considering rock creep behaviors determination［J］.Chinese Journal of Rock Mechanics and Engineering，2010，29(Sup1):3241-3246.(in Chinese))

［16］王芝银，李云鹏.岩体流变理论及其数值模拟［M］.北京:科学出版社，2008.

［17］关宝树.隧道工程设计要点集［M］.北京:人民交通出版社，2003.

［18］夏永旭，王永东.隧道结构力学计算［M］.北京:人民交通出版社，2004.

［19］黎春林.盾构施工对土层扰动机理及其对周边环境影响研究［D］.南京:东南大学，2012.

［20］WARD W H.Ground support for tunnels in weak rocks［J］.Géotechnique，1978(2):133-170.