采用类桁架连续体的桁架结构拓扑优化方法

李霞，周克民

（华侨大学 土木工程学院，福建 厦门361021）

Michell桁架是精确的理论解，经常被用来检验各种数值优化方法的正确性，但由于没有一般的求解方法，求解困难［1-3］.因此，许多数值方法大多采用有限元数值分析方法［4-7］.为了克服数值不稳定问题，陆续提出了周长控制、梯度控制等方法［8］.这些方法不仅增加了计算量，而且计算过程中的一些控制参数事先难以估计，不适当的参数可能会得不到有意义的结果.Michell理论已经揭示了拓扑优化结构的类桁架性质，拓扑优化结构理论上一般是非均质各向异性连续体.因此，上述优化方法所采用的各向同性材料无法精确描述这种拓扑优化结构.一些学者［9-11］将问题完全放松，采用一般各向异性材料模型.但是这种材料与工程结构没有明确的对应关系，后期处理困难，而且也没有反映类桁架结构的本质.本文提出有限元优化类桁架连续体方法，解决了求解困难［12-15］.

1 类桁架连续体离散化

1.1 类桁架连续体中杆件的分布性质

按照Michell理论，拓扑优化结构是由无限细、无限密杆件构成的类桁架连续体.习惯上将杆件在单工况应力约束下的优化分布区域分为5种：单向拉伸（R+）、单向压缩（R-）、各向均匀拉伸（S+）、各向均匀压缩（S-）和两向分别拉压（T）.如果不区分拉压，去掉上角标中的符号，可归纳为3类：单向拉压（R，杆件沿拉压方向），各向均匀拉压（S，杆件沿任意方向）和两向分别拉压（T，杆件沿拉压两个方向）.对于多工况或其他约束，杆件优化分布性质有所不同.将以上杆件优化分布划分方式推广到更一般的情况，其中：S区域仍然表示杆件任意分布；R区域表示杆件沿某个单一方向分布；而T区域表示杆件沿某几个确定方向（不限于2个，也不一定正交）分布.这种划分方式可以包括杆件所有分布情况.S区域由于杆件优化方向是任意分布的，所以不需要研究其优化方向，实际优化问题中也不常见.但是，实际优化问题中会经常遇到S区域退化为1个孤立的点的特殊情况，这是一个比较特殊的情况.例如当许多杆件汇交于一点时就会出现这种情况，文中将这样的点称为“奇异点”.

在优化的杆件分布场中存在分布杆件和集中杆件两种情况.分布杆有无限多，不可能都保留.但集中杆数量有限，全部是平衡必需的，应该全部保留.

1.2 集中杆件的选择

一个力学问题有力和位移两种边界条件，在有限元计算中，各种荷载一般都要等效到结点上，形成结点集中力.在有限元分析完成后，位移边界条件也可以转化为结点集中力.一个优化问题实际上就是设计这些集中力的优化传递路径.因此，文中只讨论结点集中力的情况.结点集中力需要集中杆件传递，或者需要无限多汇交于一点的分布杆件.当无限多的分布杆件汇交于一点时，杆件在汇交点位置的方向不确定，该点就是奇异点（S区）.因此，集中力作用点（包括位移约束结点，以下不再特别说明）的位置必然有集中杆件或是奇异点.从平衡的角度看，由于集中杆件也可以理解为集中力，所以集中杆件的端部必然是集中力或奇异点，选择所有集中力作用点和奇异点作为集中杆可能经过的位置，在这些位置上布置杆件就可以将所有集中杆件选择上.

确定奇异点位置的杆件方向比较困难，需要进一步分析.分布杆的奇异点位置的杆件方向不确定，由于集中杆的两端只能是集中力或奇异点，而集中力和奇异点的数量是有限的，所以为了将两个端点都位于奇异点位置的集中杆件也选上，在每个奇异点位置分别选择指向其他每个奇异点方向的杆件.

1.3 分布杆件的选择

无论是集中杆件还是分布杆件，由于仅考虑轴力而不考虑弯矩作用，曲杆仅在杆端力的作用下不能平衡，必须借助横向分布杆件.因此，在曲杆的横向应该有分布杆件.

在形成杆系结构过程中，分布杆件选择要适当.杆件选多了可以减少误差，更接近理论解，但过多的杆件并不实用.选择的标准是用最少的杆件实现最小的误差.

分布杆与集中杆结构的体积误差，如图1所示.图1（a）中：曲线AB表示一段集中曲杆；曲率半径为R；圆心角为2α；圆心为O；A，B两端的集中力F分别为沿圆弧在A，B点的切向.如果曲杆AB不受弯矩作用，在扇形ABO区域内应有径向分布杆，即Michell桁架的一个扇形段，使得圆弧杆的横向受到分布应力σ的作用，它传递A，B和O3点集中力在理论上的最优传力路径［13］.根据圆弧杆AB的竖向平衡条件，可以知道这些分布杆件的合力作用在O点，大小为2Fsinα.假设这个扇形区域内有均匀径向应变ε，材料的弹性模量为E，那么，所需材料体积为Vm＝（4FR／Eε）α.

1.4 离散杆件系统体积误差估计

采用图1（b）所示的三角形离散桁架来代替图1（a）所示的理论上的分布杆，由平衡关系，图1（b）中各杆件的轴力为

图1 分布杆与集中杆结构的体积误差Fig.1 Volume error between distributed and concentrated members

在同样的应变场下，三角形离散桁架的体积为

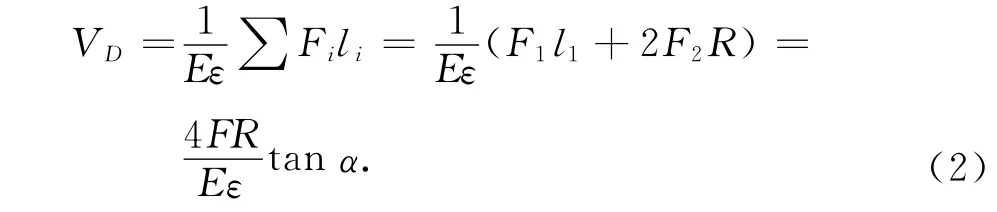
由式（2）减式（1），得到两个结构的体积误差，即

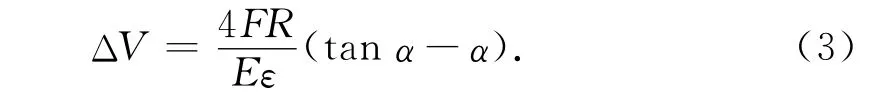
如果离散结构的杆件较多，其圆心角不会太大，可以利用三角函数的展开式，即

将式（4）代入式（3），得

由图1（a）的平衡关系，得

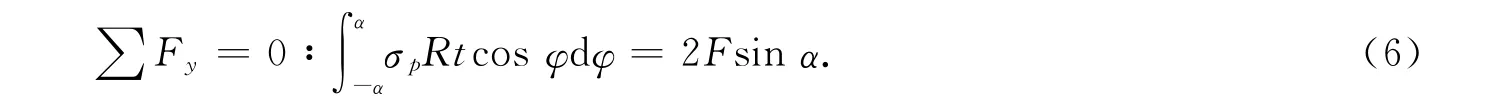
式（6）中：t是径向杆件在环向截面上的杆件密度.作为近似估计，假设密度是线性变化，则

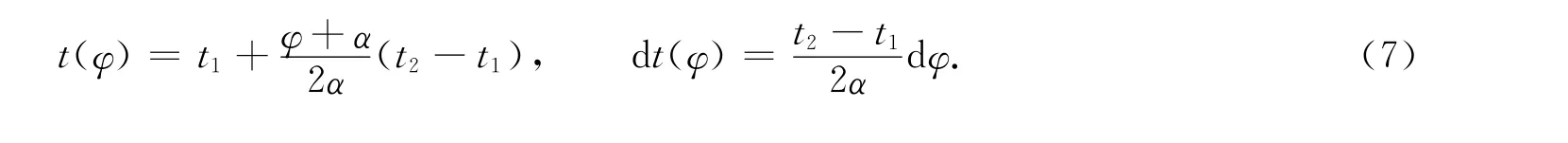
将式（7）代入式（6）的积分表达式，得

再将式（8）代入式（6）中，得

最后，将式（9）代入式（5）中，得

式（10）中：s为弧；¯t为径向杆件的横截面平均面积.

结点i位置的径向杆件在环向截面的密度记作为ti，角度为αi.结点i与结点i-1之间的单元边界长为si.结点1到k之间径向杆件的平均环向截面面积的计算式为

将式（11）代入式（10）中，得

由离散杆系代替连续分布杆件引起的体积增加量（ΔV）作为控制条件，决定离散杆件的选择.

2 算法的实现

2.1 离散杆系结构

由于集中杆件的端部一定是集中力或奇异点，所以在每个集中力作用点布置杆件，并且所有奇异点之间连接杆件就可以保证所有集中杆件都被选择上.由于分布杆件无限多，不能全部保留，只能保留相距一定间距的部分杆件.将其余的分布杆件集中到被保留的杆件上.确定杆件间距的依据就是使式（12）为常数.此外，还有2点需要说明.

1）在奇异点附近，杆件向奇异点汇交，因此该区域的杆件变化较大.因为集中力作用点附近会有应力集中，计算误差也会较大.根据奇异点的性质，在奇异点附近的杆件方向做特别的处理.当杆件进入奇异点附近时，杆件方向一律直接与奇异点相连.进入奇异点附近的标准是杆件与奇异点的距离小于单元边长的一半.

2）由于存在数值计算误差，没有材料部分的杆件密度会比0大一些.特别是对于位移约束结点，设定一个阀值，当密度低于阀值时认为没有杆件了.

2.2 奇异结点的判断

在形成离散结构过程中，判断奇异点是一个比较困难的问题.从理论上讲，杆件汇交点就是奇异点.但是，由于数值计算误差的存在，计算结果并不能保证相邻几个结点的杆件恰好相交于奇异点.奇异点判断，如图2所示.图2中：假设结点i是奇异点；围绕结点i的所有结点（称为相邻结点）为j，j∈Ji；相邻结点与结点i同属于一个单元，包括没有边联接的结点2；密度足够大的杆件都汇交结点i.奇异点是汇交点，所以密度应该比周围的密度大.结点j密度最大方向杆件所在直线到结点i的距离应足够小.两个连续的相邻点和奇异点就构成属于S区域的一个子域，为了避免误判，要求至少存在2个这样的连续子域.

图2 奇异点判断Fig.2 Judgment of singular node

2.3 确定潜在杆件的过程

1）选择所有集中力作用结点包括位移约束结点，沿着杆件密度足够大的方向画线段，交于单元的边界作为线段终点.由该线段终点所在单元边界两端的结点处的杆件密度和方向，插值得到线段终点处的杆件密度和方向.

2）为了提高计算精度，取线段起点和终点的杆件方向的平均值，从起点重新画该直线，得到修正的线段.

3）以该线段终点为下一线段的起点画下一段线段，直到域边界或密度过小，得到若干直线段连接而成的折线.

4）重新沿该折线逐段计算式，累计达到指定值标记一个“结点”；再计算下一段，得到若干结点.

5）分别从这些结点开始，沿横向画另一组折线；

6）重复过程1）～3），得到一个曲线网络.曲线网络相交点作为结点，用直线代替两个结点之间的折线构成离散桁架.

3 算例

力学模型，如图3所示.图3中：矩形设计域左边固定；上边作用两个集中力.按照满应力准则，任意位置的应变不超过允许应变.当离散后的结构杆件足够多，应变差异应该不大由于拓扑优化结果与力和尺寸大小无关.集中力（n）的大小分别取-2，-1，0，2，当n从0到2之间变化时，拓扑优化结果差别不大.因此，没有给出n＝1的结果.采用40×20矩形单元，优化的杆件分布场和离散桁架，如图4所示.图4中：左列给出杆件的优化分布；线段长度表示杆件密度；线段方向表示杆件方向；右列给出对应的拓扑优化离散杆系结构.离散杆系结构中的杆件数量可以根据需要选择，粗线表示压杆，细线表示拉杆.结果与理论解［2，4］比较接近.

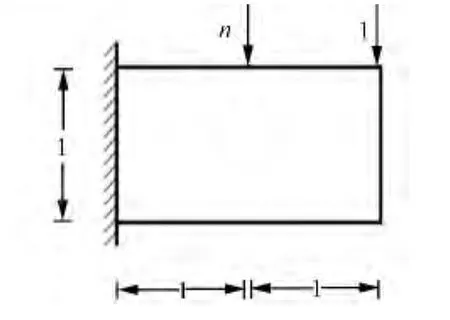
图3 力学模型Fig.3 Mechanics model

图4 优化的杆件分布场和离散桁架Fig.4 Optimum truss-like continua and their discrete truss

4 结束语

研究了基于类桁架材料模型的杆系结构拓扑优化方法.类桁架优化过程中没有抑制中间密度，完全避免了数值不稳定问题.杆系结构通过选择类桁架中的部分杆件形成，杆件的数量可以直观地控制，从而得到满足工程需要的结构.将桁架结果按照截面相等的原则转化为等厚带孔板，结果同样会比均匀化等以单元表示结构拓扑的方法更精确，效率更高，具体实现方法是下一步要进行的工作.

［1］ MICHELL A G M.The limits of economy of material in frame structure［J］.Philosophical Magazine，1904，8（6）：589-597.

［2］ LEWINSKI T，ZHOU M，ROZVANY G I N.Extended exact solutions for least-weight truss layouts（Part I）：Cantilever with a horizontal axis of symmetry［J］.International Journal of Mechanical Sciences，1994，36（5）：375-398.

［3］ ESCHENAUER H A，OLHOFF N.Topology optimization of continuum structures：A review［J］.Applied Mechanics Reviews，2001，54（4）：331-389.

［4］ ROZVANY G I N.Exact analytical solutions for some popular benchmark problems in topology optimization［J］.Structural Optimization，1998，15（1）：42-48.

［5］ ROZVANY G I N，BENDSOE M P.KIRSCH U.Layout optimization of structures［J］.Applied Mechanics Reviews，1995，48（2）：41-119.

［6］ BENDSOE M P，KIKUCHI N.Generating optimal topologies in structural design using a homogenization method［J］.Computer Methods in Applied Mechanics and Engineering，1988，71（2）：197-224.

［7］ XIE Yin-min，STEVEN G P.A simple evolutionary procedure for structures optimization［J］.Computers and Structures，1993，49（5）：885-896.

［8］ SIGMUND O，PETERSSON J.Numerical instabilities in topology optimization：A survey on procedures dealing with checkerboards，mesh-dependencies and local minima［J］.Structural Optimization，1998，16（1）：68-75.

［9］ HORNLEIN H R E M，KOCVARA M，WERNER R.Material optimization：bridging the gap between conceptual and preliminary design［J］.Aerospace Science and Technology，2001，5（8）：541-554.

［10］ HSU Y，SHO M，CHEN Chuan-tang.Interpreting results from topology optimization using density contours［J］.Computers and Structures，2001，79（10）：1049-1058.

［11］ MATSUI K，TERADA K.Continuous approximation of material distribution for topology optimization［J］.International Journal for Numerical Methods in Engineering，2004，59（14）：1925-1944.

［12］ ZHOU Ke-min，LI Xia.Topology optimization for minimum compliance using fiber-reinforced composite material model［J］.Structural Optimization，2006，37（1）：49-56.

［13］ ZHOU Ke-min，LI Jun-feng.Topology optimization of structures under multiple load cases using fiber-reinforced composite［J］.Structural Optimization，2008，38（5）：525-532.

［14］ PRAGER W.A note on discretized Michell structures［J］.Computer Methods in Applied Mechanics and Engineering，1974，3（3）：349-355.

［15］ ZHOU Ke-min，LI Jun-feng.The exact weight of discretized Michell trusses for a central point load［J］.Structural Optimization，2004，28（1）：69-72.