具有脉冲的非线性微分方程边值问题的多个正解
吴丽娇,王全义
(华侨大学 数学科学学院,福建 泉州362021)
脉冲微分方程是微分方程中一个新的分支,它在物理、化学、生物医学、工业机器人技术和经济学中都有很好的应用.脉冲微分方程边值问题的正解的存在性问题受到许多学者的广泛关注[1-10].例如,文献[5]运用锥压缩与不动点定理,研究以下一类具有脉冲的一阶微分方程边值问题
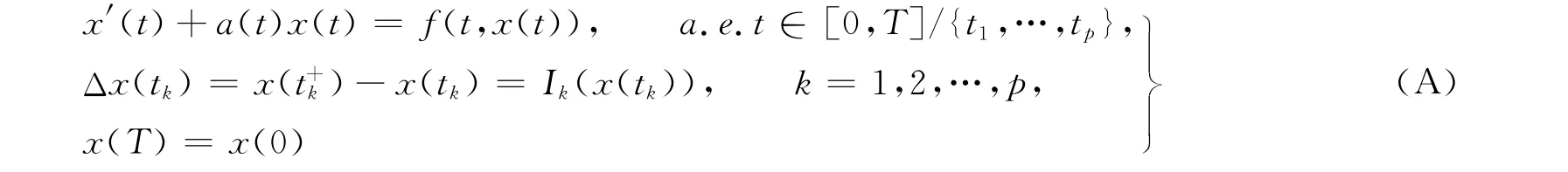
正解的存在性问题.其中:0=t0<t1<…<tp<tp+1=T,f∶[0,T]×[0,+∞)→[0,+∞)是一个脉冲Caratheodory函数,Ik∶[0,+∞)→[0,+∞)是连续的.
文献[10]运用锥压缩与不动点定理,研究具有脉冲的一阶非线性微分方程边值问题
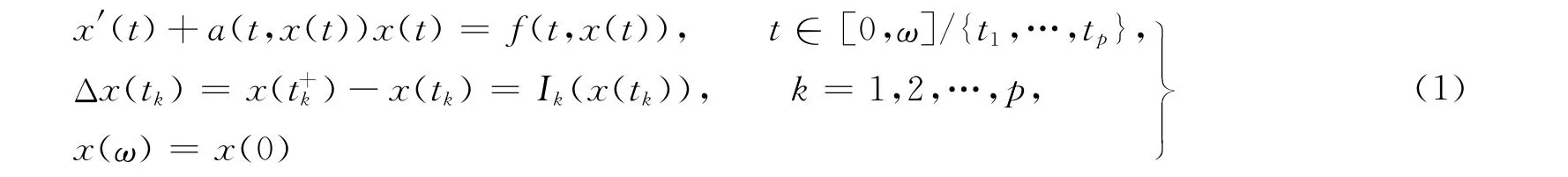
的正解存在性问题.其中:0=t0<t1<…<tp<tp+1=ω;a∶[0,ω]×[0,+∞)→R连续;Ik∶[0,+∞)→[0,+∞)(k=1,…,p)是连续的;f∶[0,ω]×[0,+∞)→[0,+∞);ω>0是常数.所得结果推广并改进了文献[5]的相关结果.本文利用Avery-Henderson不动点定理以及一些分析技巧,得出了该脉冲非线性微分方程的边值问题存在多个正解的一些充分条件的新结果.
1 预备知识及引理

定义1 设X是一个Banach空间,K是X中的一个非空子集,且满足:1)对任意的x,y∈K和实数α,β≥0,有αx+βy∈K;2)若x,-x∈K,则x=0.那么称K为X中的一个锥.
定义2 设X是一个Banach空间,K是X中的一个锥.定义K上的偏序:如果对任意的x,y∈K,x≤y当且仅当y-x∈K.
定义3 设X是一个Banach空间,K是X中的一个锥.如果映射φ∶K→[0,+∞)满足对任意的x,y∈K,x≤y,就有φ(x)≤φ(y),则称映射φ是锥K上的一个非负连续的增泛函.
假设φ是锥K上的一个非负连续的增泛函,K⊂X,∀d>0,记集合K(φ,d)={x∈K|φ(x)<d};∂K(φ,d)={x∈K|φ(x)=d};K(φ,d)={x∈K|φ(x)≤d}.
引理1[11](Avery-Henderson)设K是X中的一个锥.令γ,φ是K上的非负连续增泛函,θ是K上的非负连续泛函,其中θ(0)=0.存在常数c>0和M>0,对∀x∈K(γ,c),使得γ(x)≤θ(x)≤φ(x),‖x‖≤Mγ(x).假设存在一个全连续算子T∶K(γ,c)→K,对常数0<a<b<c,0<λ<1及x∈∂K(θ,b)满足θ(λx)≤λθ(x),且
1)γ(Tx)>c,当x∈∂K(γ,c)时;
2)θ(Tx)<b,当x∈∂K(θ,b)时;
3)φ(Tx)>a及K(φ,a)≠φ,当x∈∂K(φ,a)时,则算子T在K上至少存在两个不动点x1,x2∈K(γ,c)使得a<φ(x1),θ(x1)<b,b<θ(x2),γ(x2)<c.
引理2[11](Avery-Henderson)设K是X中的一个锥.令γ,φ是K上的非负连续增泛函,θ是K上的非负连续泛函,其中θ(0)=0.存在常数c>0和M>0,对∀x∈K(γ,c),使得γ(x)≤θ(x)≤φ(x),‖x‖≤Mγ(x).假设存在一个全连续算子T∶K(γ,c)→K,对常数0<a<b<c,0<λ<1及x∈∂K(θ,b)满足θ(λx)≤λθ(x),且
1)γ(Tx)<c,当x∈∂K(γ,c)时;
2)θ(Tx)>b,当x∈∂K(θ,b)时;
3)φ(Tx)<a及K(φ,a)≠φ,当x∈∂K(φ,a)时,则算子T在K上至少存在两个不动点x1,x2∈K(γ,c)使得a<φ(x1),θ(x1)<b,b<θ(x2),γ(x2)<c.
下面令


定义4 函数f∶[0,ω]×[0,+∞)→[0,+∞)是一个L1-Caratheodory函数,如果1)对于∀u∈R,f(·,u)∈X;2)对于t∈[0,ω],f(t,·)是连续的;3)对于每个q>0,都存在hq∈L1[0,ω],使得对于t∈[0,ω],0≤u≤q,有|f(t,u)|≤hq(t).
假设条件 H2)函数f∶[0,ω]×[0,+∞)→[0,+∞)是一个L1-Caratheodory函数成立.
引理3[10]如果条件H2)成立,则对于任意的u∈X且u(t)≥0,θk∈R,下列脉冲微分方程的边值问题

有一个解,即

其中

假设函数a1(t),a2(t)满足条件 H1),现在定义函数

令
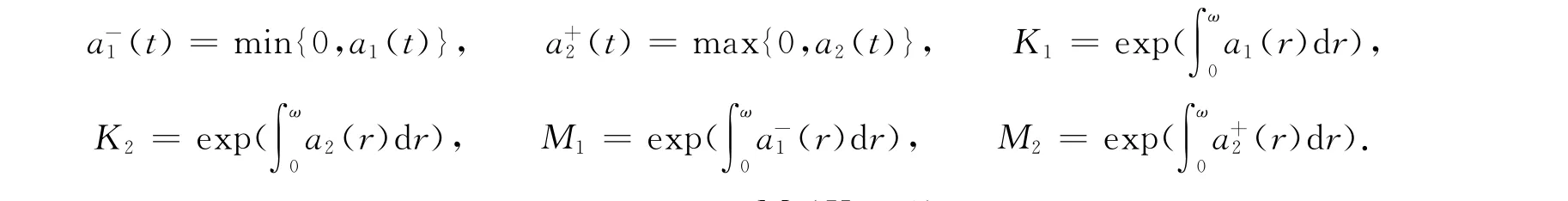

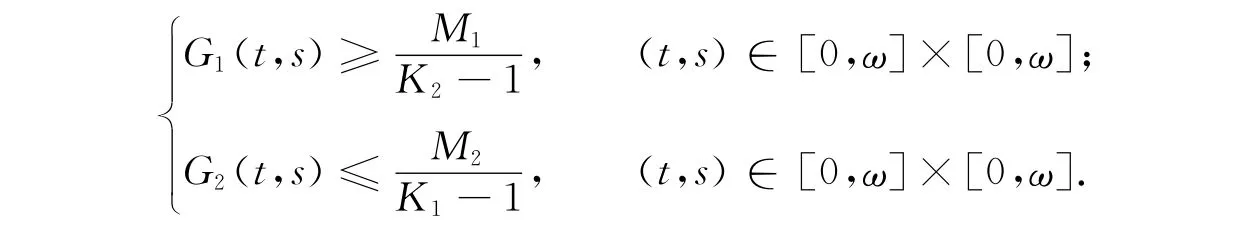
由a1(t),a2(t),a(t,x),G1(t,s),G2(t,s)的定义即得到如下引理4.
引理4 如果条件 H1),H2)成立,则对任意x∈X,(t,s)∈[0,ω]×[0,ω],有

定义算子T∶K→X为
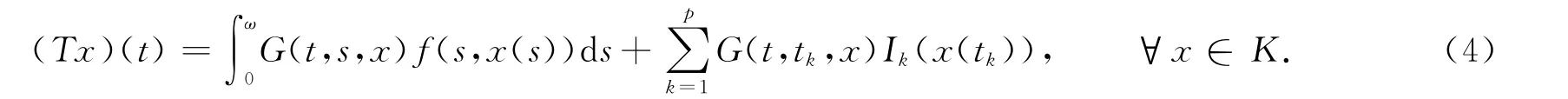
显然有T∶K→X.
引理5 如果条件H1)成立,则算子T∶K→K.
由于文中的锥K是文献[10]中的锥K的一个子集,且文中的算子T与文献[10]中的算子T的表达式相同,故由文献[10]中的引理6立即得到如下的引理.
引理6 如果条件H1),H2)成立,则算子T∶K→K是全连续的.
2 主要结果及证明
首先,取正数l1,l2满足0<l1<t1<l2<t2<ω,再取下列正数

并定义如下一些泛函,即
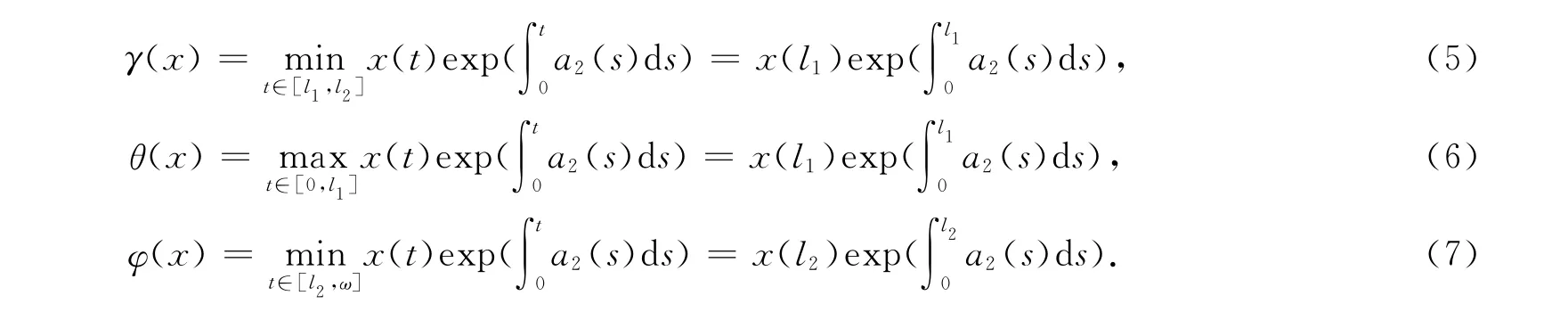
其中,x∈K.则显然如下命题成立.
命题1 i)γ,θ,φ是关于x∈K的非负连续增泛函;
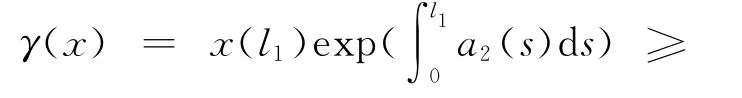
iii)对λ∈[0,1],有θ(λx)≤θλ(x).
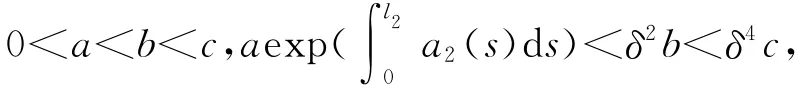

证明 考虑由式(4)定义的算子T∶K→X.由引理5和引理6易知T∶K(γ,c)→K且T是全连续的.再考虑由式(5)~(7)定义的K上的3个非负连续增泛函γ(x),θ(x),φ(x).
下面证明算子T满足引理1中的所有条件.

由命题1的结论ii)可知:当x∈∂K(γ,c)时,可以得到


其中,x∈∂K(γ,c).即引理1的条件1被满足.
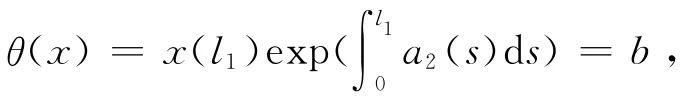

①分娩方式:统计两组产妇自然分娩率、难产率和剖宫产率。②产程进展:比较两组产妇第一产程、第二产程时间。③分娩结局:比较两组产后出血、新生儿窒息、早产、新生儿死亡发生率。其中,产后出血指胎儿娩出后2 h产妇阴道出血量>500 mL;新生儿窒息指新生儿出生后1 min Apgar评分<7分。
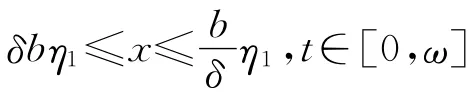

其中,x∈∂K(θ,b).即引理1的条件2被满足.
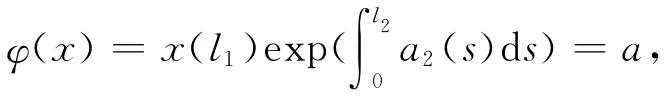

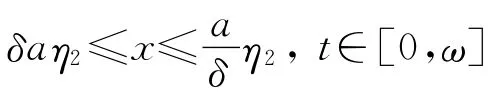

其中,∀x∈∂K(φ,a).即引理1的条件3被满足.

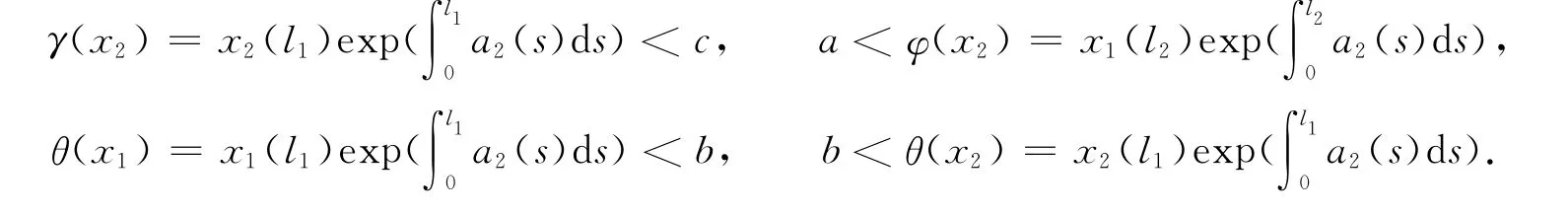
为了得到另一个新结果,取正数l1,l2满足0<l1<t1<l2<t2<ω,并定义如下一些新泛函(为简单起见,仍然采用前面的符号).即有
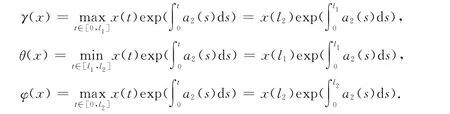
其中,x∈K.则显然如下命题成立.
命题2 i)γ,θ,φ是关于∀x∈K的非负连续增泛函;
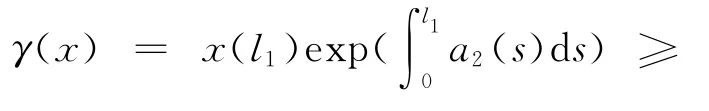
iii)对λ∈[0,1]有θ(λx)≤λθ(x).
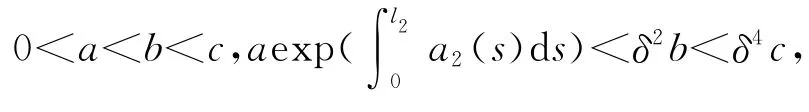

那么脉冲边值问题(1)至少存在两个正解x1,x2∈K(γ,c),使得x1(l2)>aη2,x1(l1)<bη1,x2(l1)>bη1,x2(l1)<cη1(因篇幅限制,证略).
[1] NIETO J J.Basic theory for nonresonance impulsive periodic problems of first order[J].Journal of Mathematical A-nalysis and Applications,1997,205(2):423-433.
[2] ZHAO Ai-min,BAI Zhen-guo.Existence of solutions to first-order impulsive periodic boundary value problems[J].Nonlinear Analysis,2009,71(5/6):1970-1977.
[3] NIETO J J.Periodic boundary value problems for first order impulsive ordinary differential equations[J].Nonlinear Analysis,2002,51(7):1223-1232.
[4] LIU Yang-shen.Periodic boundary value problems for first order functional differential equations with impulsive[J].Journal of Computational and Applied Mathematics,2009,223(1):27-39.
[5] LIU Yu-ji.Positive solutions of periodic boundary value problems for nonlinear first-order impulsive differential equations[J].Nonlinear Analysis,2009,70(5):2106-2122.
[6] LI Jian-li,SHEN Jian-hua.New comparison results for impulsive functional differential equations[J].Applied Mathematics Letters,2010,23(4):487-493.
[7] NIETO J J.Impulsive resonance periodic problems of first order[J].Applied Mathematics Letters,2002,15(4):489-493.
[8] ZHANG Feng-qin,MA Zhi-en,YAN Ju-rang.Periodic boundary value problems for first order impulsive delay differential equations with a parameter[J].Journal of Mathematical Analysis and Applications,2004,290(1):213-223.
[9] LI Jian-li,NIETO J J,SHEN Jian-hua.Impulsive periodic boundary value problems of first-order differential equations[J].Journal of Mathematical Analysis and Applications,2007,325(1):226-236.
[10] 吴丽娇,王全义.具有脉冲的一阶非线性微分方程边值问题的正解[J].华侨大学学报:自然科学版,2012,33(3):342-347.
[11] AVERY R I,HENDERSON J.Two positive fixed points of nonlinear operations on ordered Banach spaces[J].Comm Appl Nonlinear Anal,2001,8(1):27-36.

