城市交通的热传导分布模型研究*

王伟珠

（辽宁对外经贸学院基础课教研部，辽宁大连 116052）

城市交通的热传导分布模型研究*

王伟珠

（辽宁对外经贸学院基础课教研部，辽宁大连 116052）

运用热传导理论来建立城市交通分布模型，并通过平面热传导方程来对建立城市交通分布模型的可行性进行了研究，给出了热传导分布模型及初始条件和求解方法.

交通规划；交通预测；交通分布模型；热传导分布模型

交通分布预测是交通需求预测的关键.对于交通分布模型已经开发出好多种，如重力模型、熵模型、平衡模型、Logit模型等，并且应用在实际的规划中也都取得了不错的效果，但都存在一定的局限性.因此进一步完善交通分布的模型，建立更准确的交通分布预测理论很有必要.

1 交通分布模型的重要性

预测分布矩阵的方法还在不断发展.交通分布的预测在交通规划中占有中心的位置，掌握了一个城市未来交通的分布矩阵，进行交通规划就十分主动了，反之，不能正确估计未来交通的OD矩阵，规划就失去了指南，就会产生重大失误.可见深入比较、分析、研究各种分布模型，不断积累资料，经常修正OD矩阵，在交通规划中是十分重要的.

交通分布的研究中预测未来OD矩阵比预测交通生成的数据多得多，目前最为广泛应用的分布模型有三种，总结如下：

第一种是平均增长系数法.它在预测未来OD矩阵前，需要事先估计出各小区的交通生成量和交通吸引量.

第二种常用的模型是重力模型.交通分布预测重力模型（Gravity Model）是：

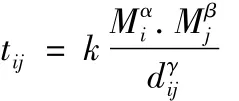
重力模型与万有引力定律十分相似，只是增加了几个待定常数.为了标定这些参数，要利用现状OD表的tij，现状交通的生成和吸引因素Mi和Mj，距离OD矩阵dij.在准备好这些数据后，再对重力模型取对数将其线性化，然后就可以利用多元线性回归求出k，α，β，γ四个参数.

第三种模型是熵模型（Entropy Model），它的公式是：

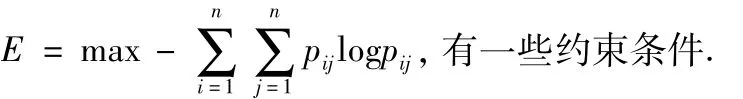
这里pij是未来OD矩阵的出行概率，pi*，p*j是未来小区交通的生成和吸引概率，它要在总交通量估计的基础上，事先计算出来.熵模型需要的条件与平均增长系数法相同，在分布预测中也常使用并有许多发展.

2 热传导方程

城市的发展是人口增加和土地的不断开发利用的结果，它往往是由一个中心开始向四周扩展，经过长期演化形成单中心或多中心城市，这和物理中的热传导现象很类似.热量总是由温度高的地方向温度低的地方扩散，热传导的结果，使温差减小，从而使熵增大.某个点的温度，对周围的区域影响较大，对距离远的地方则影响较小.这些与重力模型和熵模型有相似之处.因此，我们尝试来探讨和建立热传导分布模型.

先分析一下平面热传导方程的建立过程，函数u（x，y，t）表示物体G在位置（x，y）处及时刻t的温度，如果t固定，则u（x，y，t）是仅与（x，y）有关的温度数量场.

n＝（cosα，cosβ）T，其中α，β分别是n与x，y轴的方向夹角，ds在x，y轴上的投影分别为cosβds＝－dx，cosαds＝dy．如图1所示.小.在时刻（t1，t2）内，对传导流过闭曲线Γ的热量积分，得到区域Ω内热量变化为，

图1 法向量夹角

其中f（x，y，t）＝F（x，y，t）／cρ，（3）式称为齐次热传导方程，（4）式称为非齐次热传导方程.

热传导方程的初始条件为u（x，y，0）＝φ（x，y）；

最常用的边界条件为u（x，y，t）（x，y，t）∈Γ＝φ（x，y）．

3 城市发展的热传导分布模型

如果我们将人口的分布作为函数u（x，y，t），选取适当的传导系数a，初始条件为现状人口分布，边界条件为城市未来边界土地上的人口，热源项f（x，y，t）在旧城区取人口机械增长平均值，新城区取未来人口规划增长平均值.那么求解这个非齐次热传导方程就可以得到城市未来人口分布.人口密度与热传导现象如图2所示，

从图2可以看到，原来人口集中度很高的城市，随着城市发展，人口密度向周围扩展，这与热传导现象是一致的.

图2 人口密度与热传导现象

得到未来人口分布后，计算未来小区之间的交通OD分布量，可以采取两种方法：

（1）以现状交通OD分布为基础，令第i个小区的交通生成量为Fi，其余小区交通生成量为零，这作为初始条件，边界条件都为零.

解齐次热传导方程的Cauchy问题，得到第i个小区对第j个小区的热传导影响u（x，y，t）．如果将传导看成各方向均匀的，这时，各小区得到的交通量将只取决于与第i个小区的距离.但是，现状各小区的交通量是不同的，这种差异，正好可以用热传导系数a来包容.我们可以采用变系数，令a＝a（x，y），根据各小区获得的u（x，y，t）与实际交通量的比值，确定a（x，y）．该系数将用于计算未来两个小区的传导交通量.

方程的求解可以利用数值解法，同时也有许多软件，例如，MATLAB的偏微分方程求解模块PDETool.

这种方法，可归结为偏微分方程反问题.偏微分方程正问题，是在一定的初值与边界条件下求解非线性的偏微分方程，而反问题则是将动力模式和不同时刻观察资料作为一个整体同时考虑，充分利用两方面作用，以确定未知东西.我们利用现状OD矩阵确定热传导系数，就是一种反问题.同样地，我们还可以根据现状OD矩阵，对方程本身进行改进，提出若干新的传导扩散模式，这可更多地利用 OD矩阵的信息［1－4］.

反问题的解往往是不适定的，也就是解往往不唯一，我们要在恰当的约束下，求解它的最优解、近似解，这方面数学提供了丰富的文献和工具.

（2）直接利用现状交通OD分布矩阵，建立多维热传导方程如下：

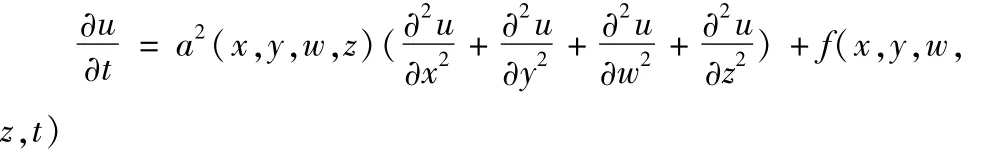
这里，（x，y）为出行起点坐标，（w，z）为出行终点坐标，u（x，y，w，z，t）为t时刻由（x，y）出发到（w，z）的交通量.

初始条件，u（x，y，w，z，0）＝T0，T0为现状OD矩阵.因为不考虑对外交通，只考虑城市内部交通，因此，当（x，y）和（w，z）在边界上时，u（x，y，w，z，t）＝0，所以可以看成边界条件为零.

对于热源项f（x，y，w，z，t），原OD矩阵的交通量tij在未来发展中总是要增长的，因此，可以近似看成线性的，例如f（x，y，w，z，t）＝ct＋d，对于老城区，d＝0，而新规划区，是在一个新的基础上增长，则d＞0．

该方法，同样要确定传导系数a，热源函数f（x，y，w，z，t）＝ct＋d中的参数.这可以先利用二元插值，加密OD矩阵，然后利用与前面相同的方式计算.该方法的表达比第一种方法更明确、简单，但是计算将比较复杂.

4 热传导分布模型与已有模型的比较

上面我们从理论上讨论了建立城市交通热传导分布模型的可行性，该模型用到了较多的数学知识，也不如三种经典模型简单，但是它有显著的优点：

（1）它描述了交通分布发展变化的过程，是动态模型，而前三种都是静态的.

（2）它既有初始条件，又有边界条件，还有可随位置和时间变化的传导系数、热源函数，同时方程本身，无论从变量个数，还是方程本身形式，都可以有多种选择.这种丰富的数学内涵，可以更好地描述交通分布的不同特征.

（3）由于它是动态模型，不仅可以得到规划年限的交通OD分布，而且可以得到各个不同年份的交通OD分布，这不仅对各阶段的规划有指导意义，更可以作为交通管理和设施建设的依据.对它的深入研究，对交通控制也具有现实意义.

5 小结

本章引入热传导理论推导出齐次热传导方程和非齐次热传导方程，指出了该方程的初始条件和求解方法，并最终利用现状交通OD分布矩阵建立多维热传导方程；最后对该模型与前述三种模型进行分析比较，总结了新的理论基础.交通规划是城市规划领域中最具科学性的部分，但是数学工具的使用还不够.结合分布模型研究，我们应该在理论探讨的同时，结合具体城市情况开展数值实验，更好地解决实际生活中的问题.

［1］毛保华，增会欣，袁振洲，等.交通规划模型及其应用［M］.北京：中国铁道出版社，1999.

［2］谷超豪，李大潜，陈恕行，等.数学物理方程［M］.北京：人民出版社，1979.

［3］郭宝琦.抛物型偏微分方程的反问题［M］.哈尔滨：黑龙江科学技术出版社，1988.

［4］陆君安，尚涛，谢进，等.偏微分方程的Matlab解法［M］.武汉：武汉大学出版社，2001.

（责任编校：晴川）

Study on the Distribution M odel for Heat Conduction

WANGWeizhu
（Liaoning University of International Business and Economics，Dalian Liaoning 116052，China）

This paper establishes the urban traffic distribution model by using heat－conduction theories，studies the feasibility of urban traffic distribution models through the heat conduction equation，and provides the heat transfer distributionmodel aswell as the initial conditions and its solutions.

transportation planning；traffic forecast；traffic distribution model；distribution model for heat conduction

U121；O172

A

1008－4681（2014）05－0017－03

2014－07－07

王伟珠（1976－），女，黑龙江哈尔滨人，辽宁对外经贸学院基础课教研部副教授，硕士.研究方向：应用数学.