线性走时插值射线追踪算法的改进＊

卢江波，方 志

（湖南大学 土木工程学院，湖南 长沙 410082）

射线追踪技术在地震层析成像以及混凝土超声波射线层析成像等领域具有重要作用.目前常用射线追踪方法主要有有限差分解程函方程法［1－2］、最短路径法［3－4］以及LTI（Linear Travel－time Inter－polation）射线追踪算法［5－6］等.实验表明［5］，LTI算法在走时计算以及射线路径追踪上比其它方法（如有限差分解程函方程法）更为快速、精确.

LTI射线追踪算法由Asakawa等人提出［5］，该算法以走时线性变化为前提，分两步进行.第一步，向前计算最小走时：先将模型划分为若干规则的单元，并将各单元边界划分为若干节段，然后，根据走时线性变化的假定以及走时最小原理（Fermat原理），求出从发射点到接收点的最小走时；第二步，根据得到的最小走时，反向追踪射线路径.但是该算法在向前计算走时时，没有考虑射线的逆向传播，不能追踪回波［9］，进而影响射线追踪的精度.针对这一问题，不少学者提出了改进算法，张东等人提出了循环计算LTI改进算法［7］，王浩全提出了交叉扫描LTI改进算法［8］，黄靓等人提出了扩张－收缩扫描改进算法［9－10］.在考虑射线的逆向传播时，文献［7－8］采用从发射点所在列向外逐列逆向扫描的方式，文献［9－10］则采用从边界列（行）向发射点所在列（行）进行逆向扫描的方式.在考虑射线的逆向传播上，文献［9－10］提出的改进算法更为合理，但是该算法存在计算效率低、收敛速度慢的问题.因为在LTI算法中，接收点要得到其最小走时，需其理论射线路径与模型单元边界所有相交节点都已得到其最小走时，这些相交节点的最小走时可能来自列扫描，也可能来自行扫描.根据本文作者对文献［5，9－10］算法步骤的理解以及对文献［9－10］中数值算例的研究，发现文献［9－10］不仅增加了从边界进行逆向传播的射线，即文献［9－10］中的收缩扫描过程，而且将文献［5］中既考虑邻列也考虑来自邻行入射射线的逐列扫描方式改为逐列（行）扫描只考虑邻列（行）入射射线的方式，这点可由文献［9］算例模型1的计算结果得出：若文献［9］的逐列（行）扫描过程既考虑邻列又考虑邻行的入射射线，则模型1经一次扩张扫描即得接收点的最小走时，此时相对误差应为0.247‰，而不应为按行列分开扫描方式经一次扩张扫描得到的计算结果3.3‰①.文献［9］采用行列分开扫描的方式使得文献［9－10］在能正确追踪回波的同时，接收点为获取其最小走时也进行了较多的无效扫描，降低了算法的计算效率.由以上分析可知，若采用行列交叉扫描的方式对扩张收缩扫描算法进行改进，将有效提高扩张收缩扫描算法的计算效率.

同时，由于绕射波以及回波的存在，文献［5］算法步骤3对每列都进行水平边界节点最小走时搜索，其意义并不明确.此外，由于扩张收缩扫描算法相比文献［5］增加了收缩扫描过程，在逐列扫描过程中能够考虑上行或下行首波的最小走时，所以文献［5］中的逐行扫描可以省略.最后，由于存在收缩扫描过程，在计算竖向边界各节点最小走时时，若按文献［5］算法步骤5的计算方法，则存在着重复无效扫描.因此，也有必要对文献［5］的扩张扫描过程进行简化和改进.

基于此，本文在前人研究的基础上提出了基于交叉扫描方式的扩张－收缩扫描新算法，该算法以扩张－收缩扫描算法为基础，结合文献［5］在逐列扫描过程中进行交叉扫描的思想，改进扩张－收缩扫描算法中逐列扫描的具体计算方法，提高了算法的计算效率，减少了迭代次数；同时，保留了原扩张收缩扫描算法的所有优点.

1 LTI射线追踪算法的基本方程

如图1所示，射线通过单元下边界的AB节段到达C节点，射线与AB的交点为D.A点及B点走时分别为TA和TB，节段AB长为L，单元慢度为s（速度的倒数），C点距A点的水平及竖向距离均为已知，分别为x，y.建立以A点为原点的局部坐标系，确定A，B，C，D点的局部坐标.现推导C点走时以及交点D 距A点长度r的计算公式［5－6］.

由线性追踪算法的基本假设可得D点的走时：

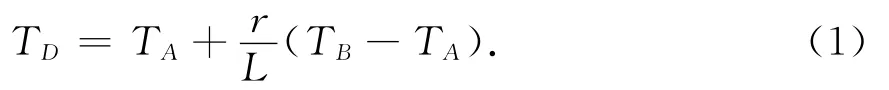
根据D点的走时，结合单元慢度以及各点的局部坐标等条件，可得C点走时：

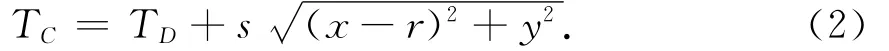
将式（1）代入式（2）得

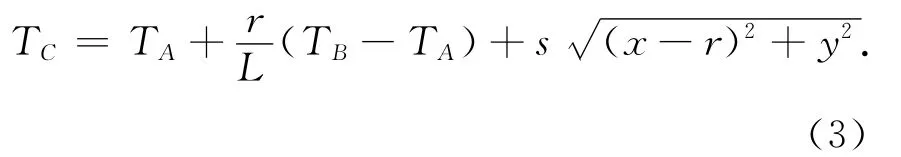
根据费马原理，TC对r的一阶偏导数应当满足等于零的条件，即（设ΔT＝TB－TA）

当L2s2－ΔT2＞0时，解方程（4）可得

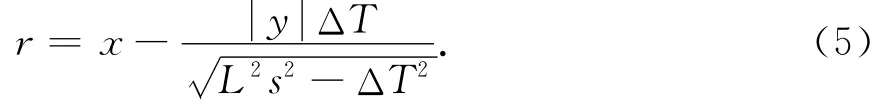
① 注：事实上，模型1接收点在按行列分开扫描的方式下，经扩张－收缩－再扩张后能够得到其最小走时，文献［9］给出的是一次扩张扫描结果，这应该是文献［9］作者的疏忽.

若r≥0且r≤L，则

若r＜0或r＞L，则计算r＝0和r＝L时的TC值，并取两者较小值作为最终TC值.

当L2s2－ΔT2≤0时，TC的计算方法与r＜0或r＞L时的情况一样.

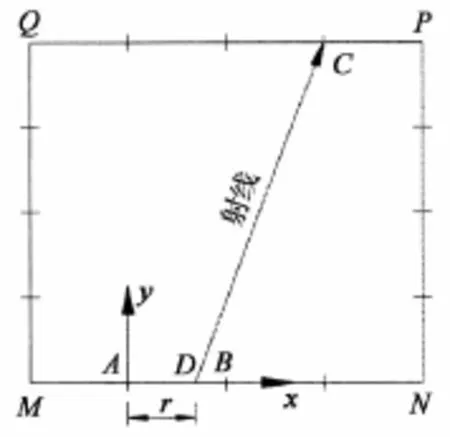
图1 经过节段AB到达C点的射线路径图Fig.1 The graph of ray path from segment ABto C

在求得r值后，可以通过A点在整体坐标系中的值推出D点在整体坐标系中的值.在这里，定义D点为C点的次级源.

2 扩张收缩扫描算法存在的问题及改进

为说明扩张收缩扫描算法［9－10］存在的问题，以图2模型为例，模型尺寸为3m×5m，单元边长及速度分别为1m和3 500m／s；单元边界划分为2个节段；发射点S位于2号单元下边界的中点，接收点为a；线段为a节点的理论射线路径，其与模型各单元边界的交点分别为d，c和b.

扩张－收缩扫描算法的第一次扩张扫描过程如图2所示（假定发射点所在列各节点的走时计算已经完成），其中图2（a）为扩张扫描的列扫描结果，图2（b）为完成所有列扫描后再进行行扫描的结果.从图2（b）可以看出a节点没有得到其最小走时.

对于a节点，此次扩张扫描为无效扫描.同时，从图2（b）还可以看出，除a节点外还有其它节点也进行了无效扫描.易知，当模型网格划分得更多时，将有更多节点经历无效扫描.

为了减少无效扫描，提高算法的计算效率.本文采用行列交叉扫描的方式对算法［9－10］进行改进，即在扩张（收缩）扫描过程，行列扫描不再分开进行，而是在其逐列（行）扫描时就同时进行行和列的扫描.仍以图2所示模型为例，采用改进后的算法对其进行一次扩张扫描，同样假定发射点所在列各节点的走时计算已经完成.

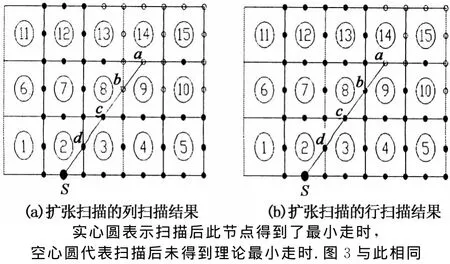
图2 扩张收缩扫描算法的扩张扫描过程及结果Fig.2 Process and results of expansion scan of expansion－contraction scanning algorithm

图3（a）为改进算法在扩张扫描时对第3列进行交叉扫描后的结果，可看出，b和c节点在这次行列交叉扫描过程中都得到了最小走时，进而在第4列进行交叉扫描后，a节点能得到其最小走时（图3（b））.

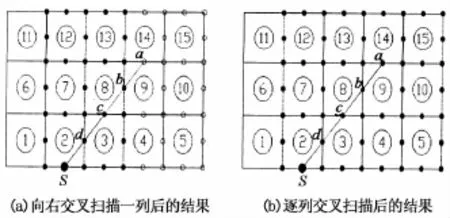
图3 改进算法的扩张扫描过程及结果Fig.3 Scanning process and results of improved algorithm

对比图2（b）和图3（b），可以看出，改进算法进行的无效扫描更少，具有更高的计算效率，同时，由于改进算法仅改变了扫描顺序，两种算法的单次扩张扫描计算量不变.同时，对比文献［5］的一次扩张扫描过程，可以看出，本文提出的交叉扫描算法仅保留了逐列扫描过程中的行扫描，去掉了逐列扫描后附加的逐行扫描过程，并对文献［5］的逐列扫描过程进行了简化.

需要说明的是，本文的交叉扫描与扩张收缩扫描在概念上是不同的，前者针对的是一次扩张收缩扫描中行列的计算次序，而后者针对的是整个单元网格的计算次序，一个为微观操作，另一个为宏观操作.下文中，除“扩张扫描”和“收缩扫描”中的“扫描”为宏观操作外，其余“扫描”均指微观操作.

3 改进算法的基本步骤

改进算法仍分两步进行，第一步向前计算走时，第二步，向后追踪射线路径，其中第二步与文献［9－10］相同，不赘述.

改进算法的基本步骤如下：

1）如图4所示，模型为3×3的网格，发射点S位于第2行第2列.以发射点所在的行和列为轴，将网格划分为四个象限，其中发射点所在行和列为各象限共有部分.图4（a）和图4（b）中的阴影部分分别为模型的第一和第二象限.

图4 模型网格及象限划分示意图Fig.4 Model grid and quadrant division schematic diagram

2）计算发射点S所在单元边界上各节点的走时，并记录次级源.假定此模型在各单元的边界上均只划分两个节段（图5），则各单元均有8个节点.根据单元节点以及发射点在整体坐标系中的坐标，可求得发射点S所在单元边界上各节点的走时，并将S点记为各节点的次级源.

3）计算发射点S所在列所有节点的走时并记录次级源.

首先计算图6中与发射点单元上边界相连的EJLG单元各节点的走时.

以I点的走时计算为例（仅考虑通过下边界GE到达I节点的射线），易知，满足I点最小走时要求的射线可能来自GE中的任一节段.此时，根据第1节给出的计算公式和计算方法分别计算出射线通过GF节段和FE节段时I点的最小走时，取两个最小走时的较小值作为I点的最小走时，并记录相应的次级源.以同样步骤求出EJLG单元其它节点的走时，完成该单元的计算.这种通过单元下边界节点走时计算其它节点走时的过程，称为向上扫描.其它通过上边界、左边界、右边界的情况分别称为向下扫描、向右扫描以及向左扫描.

图5 改进算法的基本步骤2Fig.5 The basic steps 2of improved algorithm

图6 改进算法的基本步骤3Fig.6 The basic steps 3of improved algorithm

然后，以同样的方式向上逐个计算其它单元的节点走时，并记录相应的次级源.

最后，从发射点单元开始，向下扫描，最终完成发射点S所在列所有节点走时计算以及次级源记录.

4）扩张扫描.对步骤1划分的四个象限采用不同的扫描策略，具体如下.

象限Ⅰ：从靠近发射点所在列的右侧列开始，向右逐列进行向右向上交叉扫描，直至模型的最后一列.以靠近发射点所在列的右侧列为例说明交叉扫描算法：如图7所示，先对此列单元进行向右扫描，然后再向上扫描，在扫描过程中，若扫描得到的节点走时比原节点走时小，则更新此节点的走时，并记录对应的次级源，否则，原节点走时以及相应次级源保持不变.

象限Ⅱ，Ⅲ，Ⅳ的扫描也均从发射点所在列开始，向左（象限Ⅱ，Ⅲ）或向右（象限Ⅳ）逐列进行向左向上（象限Ⅱ）、向左向下（象限Ⅲ）以及向右向下（象限Ⅳ）交叉扫描，直至模型的边界.

图7 改进算法的基本步骤4Fig.7 The basic steps 4of improved algorithm

5）收缩扫描.四个象限的收缩扫描均从模型的竖向边界开始，向左（象限Ⅰ，Ⅳ）或向右（象限Ⅱ，Ⅲ）逐列进行向左向下（象限Ⅰ）、向左向上（象限Ⅳ）、向右向下（象限Ⅱ）或向右向上（象限Ⅲ）交叉扫描，直至发射点所在列.

6）重复步骤4）和5），直到模型中所有节点的走时均不再改变为止.至此得到所有节点的最小走时以及相应的次级源.

对比文献［5］的逐列扫描过程，本文省去了对每列都进行水平边界节点最小走时的搜索，原因如前言所述，在绕射波以及回波存在的情况下，搜索水平边界节点最小走时的意义并不明确.同时，为了确定逐列扫描过程中行扫描的顺序，本文参考了均匀介质模型各节点的理论射线路径，如发射点右上方单元各节点的最小走时均来自各自单元的左边界或下边界，据此将模型划分为四个象限，这也与仅改变文献［9］行列扫描顺序的结果一致.最后，本文按象限划分扫描区域进行逐列扫描的方式较文献［5］的逐列扫描过程更简洁，程序编制也更为容易.

4 数值算例

为了验证本文提出的改进算法在计算效率上的优越性，给出三个数值算例.考虑到改进算法仅改变了扫描顺序，不改变单次扩张收缩扫描计算量，故选取计算收敛所需迭代次数为对比参数.

算例1 如图8，模型尺寸为3m×5m，各单元边长及速度分别为1m和3 500m／s，单元边界划分为2个节段，发射点S位于模型的下边界，且距模型左边界1.5m.

采用扩张－收缩扫描算法［9－10］及本文改进算法进行计算.结果显示：扩张－收缩扫描算法需进行4次迭代才收敛，而改进算法只需要2次迭代即收敛.

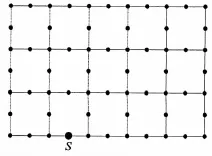
图8 算例1计算模型Fig.8 Calculation model of example 1

算例2 将算例1模型细划为30×50的网格，单元边长为0.1m.如图9所示，发射点位置不变.单元边界划分为2个节段.计算结果显示：扩张收缩扫描算法需进行31次迭代，而改进算法仍只需2次迭代.

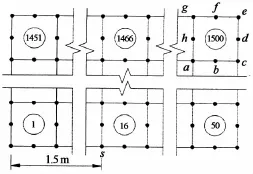
图9 算例2计算模型Fig.9 Calculation model of example 2

现将1 500号单元在两种算法下的扫描过程及结果列于表1，其中，由于算法收敛的条件，原算法及改进算法的最后一次迭代结果均与前一次的迭代结果相同.

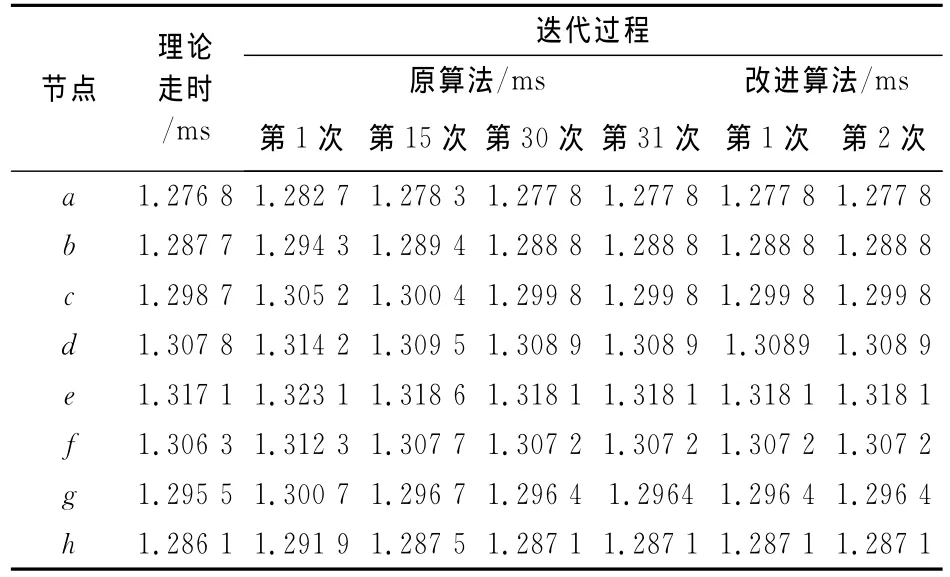
表1 1 500号单元在两种算法下的扫描过程及结果Tab.1 Scanning process and results of No.1 500under the two algorithms

算例1及算例2的计算结果表明：对于均质模型，改进算法相比于原算法具有更快的收敛速度，且当模型网格尺寸划分较细时，改进算法在计算效率上的优势更显著.

算例3 如图10，模型尺寸为20m×20m，单元边长为1m；单元速度有两种，其中白色单元的速度为3 500m／s，黑色单元的速度为100m／s，单元边界划分为2个节段，发射点S和接收点R分别位于模型的左下角和下边界距发射点6m位置.

计算结果显示：改进算法只需7次迭代即收敛，而原算法则需17次迭代；同时，接收点R在两种算法下的计算最小走时均为8.439 6ms，与理论最小走时相差0.19%.

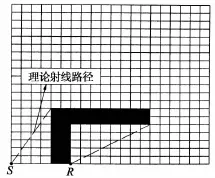
图10 算例3计算模型Fig.10 Calculation model of example 3

算例3的计算结果表明：改进算法保留了扩张收缩扫描算法能正确处理射线逆向传播的优点，并且具有更快的收敛速度.

5 结 语

理论分析以及数值算例表明，本文提出的基于交叉扫描方式的扩张－收缩扫描算法，不仅具有原扩张－收缩扫描算法的所有优点，而且在不增加单次扩张－扫描计算量的前提下，通过改变算法的扫描顺序，提高了算法的计算效率，加快了算法的收敛速度.特别当模型网格划分数较多时，改进算法在计算效率方面的优势更为显著.

［1］VIDALE J.Finite－difference calculationoftravel times［J］.Bulletin of the Seismological Society of America，1988，78（6）：2062－2076.

［2］QIN F，LUO Y，OLSEN K B，et al.Finite－differencesolution of the eikonal equation alongexpandingwavefronts［J］.Geophysics，1992，57（3）：478－487.

［3］MOSERT J.Shortest path calculation of seismic rays［J］.Geophysics，1991，56（1）：59－67.

［4］刘洪，孟凡林，李幼铭.计算最小走时和射线路径的界面网全局方法［J］.地球物理学报，1995，38（6）：823－832.LIU Hong，MENG Fan－lin，LI You－ming.The interface grid method for seeking global minimum travel－time and the correspondent ray path ［J］，Acta Geophysica Sinica，1995，38（6）：823－832.（In Chinese）

［5］ASAKAWA E，KAWANAKA T.Seismic ray tracing using linear traveltimeinterpolation［J］.Geophysical Prospecting，1993，41（1）：99－111.

［6］赵改善，郝守玲，杨尔皓，等.基于旅行时线性插值的地震射线追踪算法［J］.石油物探，1998，37（2）：14－24.ZHAO Gai－shan，HAO Shou－lin，YANG Er－hao，et al.Seismic ray tracing algorithm based on the linear traveltimeinterpolation［J］.Geophysical Prospecting for Petroleum，1998，37（2）：14－24.（In Chinese）

［7］张东，谢宝莲，杨艳，等.一种改进的线性走时插值射线追踪算法［J］.地球物理学报，2009，52（1）：200－205.ZHANG Dong，XIE Bao－lian，YANG Yan，et al.A ray tracing method based on improved linear traveltimeinterpolation［J］.Chinese Journal of Geophysics，2009，52（1）：200－205.（In Chinese）

［8］WANG Hao－quan.An improved method of linear travel－time interpolation ray tracing algorithm［J］.Acta Physica Polonica－Series A，2010，118（4）：521.

［9］黄靓，黄政宇.线性插值射线追踪的改进方法［J］.湘潭大学学报：自然科学版，2002，24（4）：105－108.HUANG Liang，HUANG Zheng－yu.An improved method of linear interpolation ray tracing［J］.Journal of Xiangtan University：Natural Science Edition，2002，24（4）：105－108.（In Chinese）

［10］黄靓.混凝土超声波层析成像的理论方法和试验研究［D］.长沙：湖南大学土木工程学院，2008：33－35.HUANG Liang.Methodology and experiment research on concrete ultrasonic computerized tomography［D］.Changsha：College of Civil Engineering，Hunan University，2008：33－35.（In Chinese）