基于模糊学分析框架的翻译标准研究
李 平
(安徽冶金科技职业学院 安徽马鞍山 243000)
“忠实或信”是翻译中的最重要的标准(当然,表述翻译标准的还有其他术语,如“化境”、“功能对等”等等),它既是译者在具体翻译过程中时时要面对的问题,也是翻译研究者们经常探讨和引起争论的问题,也正是有这样的问题才不断地推动着翻译的发展和翻译理论的建设。漫长的翻译历史和同样漫长的翻译研究史使得围绕“忠实或信”的话语绵延不断,尤其是以经验和思辨为特点的传统翻译和译论几乎就很自然地把“忠实或信”当作翻译的出发点和归宿点。
随着翻译研究的跨学科发展以及译学本身的纵深发展,使得翻译研究中的各种学科知识和各种研究方法的运用愈加广泛,其中就包括以数理逻辑和观察实验为基础的科学实证方法。本文尝试将“忠实或信”中的主观定义、描述模糊和宽泛纳入模糊数学或模糊学(Fuzzy Mathematics)数理逻辑分析框架中,尝试给出具有客观性的定义和描述。希望抛砖引玉,赐教与各位同仁。
1 关于“忠实”、“信”标准的模糊性问题
我们在运用模糊数学讨论忠实、信的模糊性之前,先介绍一下模糊数学和模糊性。
以精确数学及随机数学为基础的近代和现代科学技术最显著的特点之一就是能非常有效地定义和描述客观世界中那些界限分明的清晰事物,并能作出非此即彼的判断和进行精确测量。但是,在客观世界中还普遍存在着大量的模糊现象。比如,在日常生活中,经常遇到许多模糊事物,没有分明的数量界限,要使用一些模糊的词句来形容、描述。如比较年轻、高个、大胖子、好、漂亮、善、热、远……。再如在翻译学这样的人文学科中的一些术语概念往往是非数值的,象“忠实”、“通顺”、“信、达、雅”本质上不能象物理量那样实地测量。所以,以精确数学及随机数学为主的传统数学无法满足人文、社会学科及其它“软科学”的数学化、定量化趋向。
模糊数学作为专门描述和处理模糊性的理论和方法,我们首先要理解的一个基本概念,就是模糊性这个概念。为了识别事物,人们总要依据一定的标准对它们进行分类。在现实世界中,有许多事物可以依据精确的标准把事物分为彼此界限分明的类别,每个事物要么属于某一类,要么不属于该类,非此即彼,明确肯定,如“地球是行星”,“石头不是食物”,“翻译学是一门既包含艺术又包含科学的学科”,“这一句是直译”,都是关于事物类属的明确断言,我们通常把这类事物称为清晰事物。但是现实世界中还有许多事物和现象我们无法找到精确的分类标准,很难对某一事物是否属于某一类作出明确肯定的断言,如高山、大河,如译论中的忠实、叛逆、通顺、直译、意译、归化、异化等。由于这些事物和现象从属于某一类到不属于该类是逐步过渡而非突然改变的,不同类别之间不存在截然分明的界限,因而不同的人对同一事物或现象可能作出不同的归类。我们把事物或现象具有这种类属的不清晰性称为模糊性。
了解了模糊性,我们就可以来讨论翻译标准里的“忠实或信”的模糊性问题。我们知道翻译就是把用一种语言文字表达的思想、内容用另一种语言文字传递和表达出来。按照今天的人文学话语,传递和表达必须要做到“忠实而流畅地传递表达”或“取信于原文的传递和表达”。那么,做到如何“忠实”、“信”?这就大有文章可做了,从古人到今天,我们一直在绞尽脑汁,穷尽皓首地做这样的文章,可一直做不到百分之百的“忠实”、“信”。我们无论是翻译还是教授翻译时,都会自觉或不自觉地使用到“忠实”、“信”这样的标准,否则就不能称之为翻译了或翻译学了。
根据王东风看法(王东风,2004/6:9),“忠实”、“信”在本质上是一个伦理二元对立的概念,要么忠,要么不忠,要么信,要么不信,不存在模糊的中间状态,其实,从模糊学看,“忠实”、“信”就象“漂亮女人类”一样缺乏明确的类别隶属判据,到底什么才算“忠实”,什么才算“信”没有明确、清晰的界限,在类别隶属判据上存在着中间状态、区别程度、等级对象等,也就是说“忠实”、“信”具有模糊性。“忠实”、“信”这种模糊性是来自事物性态和类属的不确定性、不清晰性和渐变性,而这恰恰反映了世界的多样性、多元性和差异性。“忠实”、“信”在译学研究中缺乏观察、描述和解释的充分性就在于把“忠实”、“信”当作了要么忠,要么不忠,要么信,要么不信这样一个二值逻辑看待。我们知道,传统的思维逻辑基础是二值逻辑,要求对每个命题做出要么真、要么假的明确断定。这是适于处理清晰概念和命题的逻辑模式。当它用于处理模糊概念和命题时,理论上将导致逻辑悖论。根据逻辑学中最著名的秃头悖论[1],忠实与不忠实,信与不信同秃与不秃,年轻与年老一样,这些概念都有模糊性,用精确的二值逻辑描述这类概念和用这类概念构成的判断和推理,必然导致忠实是不忠实、不忠实是忠实、信是不信、不信是信的悖论。
作为一个概念和术语,“忠实或信”的模糊性源于其考察对象在性态和类属方面的亦此亦彼性,即具有中介过度性,也就是说“忠实或信”不再象以前那样具有清晰性,即不是忠就是不忠那样的非此即彼性,而是忠和不忠之间存在着许多中介过度态,即存在着许多程度不同,资格不同忠,而这许多忠的类属是不确定的,在翻译的某一方面、某一阶段表现为不忠,但到了另一方面、另一阶段就表现为忠。因此,原来对立的两极“忠”与“不忠”变成互相渗透、互相贯通,由一极到另一极之间呈现出一系列中介过度状态、环节或阶段。由此看到,所谓清晰性是相对的,而模糊性却是绝对的。我们以前用“忠实或信”标准来考察翻译研究中的对象,是把考察对象所包含的差异忽略不计就可能成为清晰,而现在用“忠实或信”来考察时,其对象所包含的差异就不能忽略不计,这时就可能形成模糊性,我们要通过了解“忠实或信”的这种差异和变化来把握所考察对象自身的同一性,比如,把“举筷”译为“to take up the chopsticks to eat”或译为“to take up a knife and fork”,把“firewall”译为“网络安全通路”或译为“防火墙”,都属于忠实或信,即译论里常讲的异化、归化以及直译、意译,或者更严格讲就是属于“忠实或信”的模糊性。
2 “忠实”或“信”的一个模糊学分析框架
要给“忠实”或“信”以适当的模糊学描述,首先需要介绍一下集合的概念,通俗地说,所谓集合,就是把一些事物汇集到一起组成一个整体,汇集在一起的事物就是这个集合的元素或成员,例如教室内的桌椅,图书馆的全部藏书的集合。通常集合用大写字母A、B、X、Y等来表示,元素用小写字母a、b、x、y等来表示。x属于A,记为x∈A;y不属于A,记为y∉A。由于在经典集合论中,集合被理解为人们直观上或思想上的那些确定的、能够彼此区分的事物汇集在一起形成的整体,所以集合也常用特征函数来表示。设集合A的特征函数,记为fA(x),定义为:
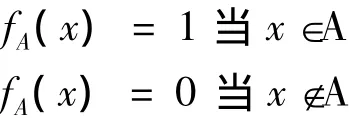
显然我们可以用集合论的数学模型来描述我们精确二值逻辑:对于任一元素x和集合A,要么x∈A,要么x∉A,二者必居其一且只居其一。这就是经典集合论对清晰事物类属关系的二值的、绝对的规定,如传统译论中的不是忠实就是不忠实这样非此即彼的二值逻辑思维。然而,经典集合论却无法描述类属不分明的模糊事物,于是就有了查德(Zedeh)把经典集合推广到模糊集合,这意味着把元素属于集合的概念模糊化,承认所考察的对象存在既非完全属于某集合,又非完全不属于该集合的元素,变绝对的属于概念为相对的属于概念。这样,不同元素对同一集合有不同的隶属程度。所以,在模糊集合中,给定范围内元素对它的隶属关系不一定只有“是”或“否”两种情况,而是用介于0和1之间的实数来表示隶属程度,存在许多中间过渡状态。比如“老人”是个模糊概念,70岁的肯定属于老人,它的从属程度是1,40岁的人肯定不算老人,它的从属程度为0,按照查德给出的公式,55岁属于“老”的程度为0.5,即“半老”,60岁属于“老”的程度0.8。查德认为,指明各个元素的隶属集合,就等于指定了一个集合。当隶属于0和1之间值时,就是模糊集合。
有了模糊集合,我们可以对“忠实”或“信”作出描述和解释。根据模糊学,翻译研究中的“忠实”或“信”实际上可以看作是一个模糊集合:完全忠、十分忠、很忠、忠、相当忠、有些忠、有点忠、不太忠、不很忠、不忠、根本不忠等等,当然这是比较通俗说法。对忠实或信的模糊集合比较严格的描述如下:
设A是论域U上的模糊集合(所谓论域是指讨论涉及的对象范围),也就是在“忠实”或“信”这个翻译标准论域上,“忠实或信”的模糊集合是用A来表示的,在论域中百分之百的忠实或信属于A的元素对A的隶属度为μ=1,百分之百的不忠实或信不属于A的元素对A的隶属度为μ=0,其余的元素对A的隶属度用介于0和1之间的实数μ来表示,较大的μ值表示较高的忠实或信的隶属度,这样,“忠实或信”的模糊集合A就得到一种定量的描述。
以“~”作为模糊化记号,模糊集合记为A、B、C、等。我们给出如下定义:译论域U上的“忠实”或“信”的模糊集合A是用一个从U到实区间[0,1]的函数μA来描述的,μA叫做模糊集合A的隶属函数②,函数值μA(x)代表元素x对集合A的隶属度。
对照经典集合,可以看到经典集合用特征函数描述,那么“忠实”或“信”特征函数值域为集合{0,1}这样的要么忠实,要么叛逆的二值或二元对立逻辑推理,而模糊集合是用隶属函数来描述的,隶属函数的值域为区间[0,1],也就是存在着不同资格、不同程度的连续过度的“忠实”或“信”,例如,把“转首肯为摇头”(邵志洪、岳俊,2005/1:74)译为:

如果设U为该句的“忠实”或“信”,设A为U上的把“转首肯为摇头”译成英语时“忠实”或“信”的模糊集合,我们得到如下隶属函数或隶属度μA(x):

x (1) (2) (3) (4)μA(x)1 0.8 0.7 0.5
所以,从“忠实”到“叛逆”之间存在着许多资格不同的忠实和叛逆这样的元素,它们从属于集合到不属于集合的渐变过程,亦即忠实或信的隶属度在“忠实”或“信”上存在着分布,这种分布反映出人们对“忠实”或“信”因不同原因或不同翻译策略而有不同的认知和理解,这不仅说明“忠实或信”的隶属度具有客观性和实证性,而且还有主观性,因为“忠实或信”的隶属度是一种非数值的量的规定性,不能象物理量那样实地测量,要求象测量长度、高度那样找到隶属度的客观标准,是不现实的,实际给出的隶属度总有一定的主观成分,不同的人对同一事物隶属度的指定常有差别,令μA((1))=0.9而不是1也未尝不可,即认为(1)不是百分之百的忠实而是百分之九十的忠实,因为可能存在比“Nodding approval will give way to head-shaking.”忠实或信隶属度更高的译文;同样,令μA((4))=0.3而不是0.5也意味着人们可能认为“Positive views will give way to negative views.”忠实不足,而叛逆有余,即(4)不是百分之五十的忠实而是有百分之七十的叛逆。可见,隶属度的这种不唯一性,是模糊性的一个特点,隶属度中包含一定主观成分给译者、译论者发挥主观能动性提供了条件,这恰恰也是传统译论里常讲到的翻译需要创造性、艺术性、丰富的经验、熟练的技巧和灵活的策略的源泉,有了这些,才能给出切合实际的隶属函数,才能应用模糊学方法尝试在科学上对“忠实”或“信”作具体的定量分析和实证研究,我们的主观性就有了客观依据,从这种意义上讲,翻译研究也有了实证研究的意义。
3 结语
长期以来,“忠实”或“信”作为译学中的术语和标准,一直用于译学研究和探讨,随着译学研究和探讨的不断发展,人们对“忠实”或“信”内涵和外延认识也在深入,把“忠实或信”放入模糊学分析框架,运用模糊集合对“忠实”或“信”作出定量分析,是我们的一个尝试,通过这一尝试,我们希望能对“忠实或信”这样的标准上有更多的客观的和实证的描述,隶属函数的定量实证分析使得“忠实或信”这样翻译标准的主观性、人文性的描述具备量化实证的客观依据,从而有可能对翻译标准作出科学的解释和探索。
注释:
①秃头悖论:日常生活中,某人是否秃头是容易判断的。要给秃和不秃下精确定义,却难乎其难。按照传统逻辑,有两种方案可供选择:(1)承认存在一个作为界限的头发根数n 0,n即实际的头发根数,规定n≤n 0时为秃头,n>n 0时为不秃。但一发之差便分秃与不秃,为常识所不容,这样的n 0不存在。(2)承认一发之差不改变秃与不秃,这似乎合乎常识。从常识看,命题A“比秃头多一根头发还是秃头”,命题B“比非秃头少一根头发者还是非秃头”,都是真命题。命题α“一发皆无(n=0)者是秃头”,命题β“满头乌发者(例如n=1000000)是非秃头”,显然也都是真命题。但是,从命题A和命题α出发,按传统逻辑的推理规则作连锁推理,可以得出显然为假的命题δ“满头乌发者是秃头”;从命题B和命题β出发,又可推出显然为假的命题ε“一发皆无者是非秃头。这就导致了悖论。同样可以出现年龄悖论:由显然为真的命题“20岁的人是年轻人”和“比年轻人早生一日的人还是年轻人”可以推出显然为假的命题“百岁老人是年轻人”。
②如读者熟悉现代数学映射概念,就有以下更为严格的定义:
论域U到实区间[0,1]的任一映射

都确定U上的一个模糊集合A,μA叫做A的隶属函数,μA(x)叫做x对A的隶属度。
[1]楼世博,孙章,陈化成.模糊数学[M].北京:科学出版社,1983
[2]左孝凌.离散数学[M].北京:经济科学出版社,2000
[3]苗东升.模糊学导引[M].北京:中国人民大学出版社,1987
[4]贺仲雄.模糊数学及其应用[M].天津:天津科学技术出版社,1983
[5]王东方.解构“忠实“——翻译神化的终结[J].中国翻译,2004.6
[6]司显柱.译作一定要忠实原作吗?——翻译本质的再认识[J].上海科技翻译,2002.4
[7]邵志洪,岳俊.英汉语篇衔接对比与翻译策略[J].中国翻译,2005.1
[8]李平.翻译学信息范式研究[J].中国科技翻译,2000.3
[9]Zadeh,L.A.Fuzzy Sets[J]Inf.Control,8(1965).
[10]Zadeh,L.A.Fuzzy Algorithms[J]Inf.Control,12(1968).
[11]Zadeh,L.A.A New Approach to System Analysis in Man and Computer[M]North-Holland,Amsterdam,1974.

