一种基于平均周期图的频域信噪比估计算法*
胡冰舟,张 蓉,雷维嘉,谢显中
(重庆邮电大学移动通信技术重庆市重点实验室,重庆400065)
1 引言
信噪比作为衡量信道质量的重要参数之一,其研究一直受到广泛的关注。在通信系统中,很多环节都需要信噪比的先验知识来进行性能优化,如调制和编码方式的选择,蜂窝网中越区切换、功率控制和信道分配等。
现有的信噪比估计算法从采用的信号处理方法的角度可以分为最大似然估计法[1-4]、二阶四阶矩(M2M4)估计法[5-6]、高阶累积量估计法[7]、多项式拟合法[8-9]和频域估计法[10-11]等,其中前 4 种都是时域算法。最大似然估计法可对输入匹配滤波器的过采样数字信号进行估计,也可对输入判决器的符号间隔采样数字信号进行估计。文献[2]针对MPSK信号,对使用上述两种信号时,在复AWGN条件下的信噪比估计性能进行对比,证明在数据辅助条件下,最大似然算法最优;而无数据辅助时,在高信噪比时有较好的性能,但低信噪比时性能明显下降。文献[3]提出一种基于迭代的信号幅度和信噪比联合估计算法,改善了由判决错误导致的估计偏差,性能接近数据辅助类算法。该方法提高了低信噪比时的估计精度,但复杂度也增加了。最大似然法估计精度较高,但其不适用于非恒包络信号。接收机的本地载波与接收信号载波有频差时,最大似然算法也不适用。
文献[5]给出一种改进的M2M4估计法,在一定的信噪比范围内估计偏差很小,但该信噪比范围较小。文献[7]研究了高阶统计量的盲信噪比估计算法,改善了M2M4算法在高阶调制时和高信噪比下的性能,但是其估计范围也不大。多项式拟合法是一种重要的盲信噪比估计法,文献[8]利用数据曲线拟合的方法对基于矩特征的信噪比估计进行了改进,得到了较好的估计性能。频域估计算法使用符号采样前的信号,在频域中对信噪比进行估计。此算法利用只有噪声的频段计算出噪声功率,信号功率可由总功率与噪声功率的差得到。文献[10-11]比较了频域信噪比估计法和其他方法的性能,与其他方法相比,频域估计法处理过程简单,计算量相对较少,有较高的估计精度。
由于上述文献中信噪比估计算法出现复杂度高、估计范围窄、低信噪比下估计精度低或者应用范围有限等问题,本文对低信噪比条件下的频域估计算法进行分析,给出一种基于平均周期图的频域估计算法,该算法运算量少,复杂度低。Matlab仿真结果表明,本文算法在低信噪比下可以实现较准确估计,并且应用范围广,不受多普勒频移影响。
2 频域信噪比估计算法
频域估计法适用于白噪声并已知信号频带的情况,如果信号频带未知,也可通过信号的频谱特性估计出来。白噪声信道下的接收信号中,噪声功率谱密度在整个频带内为均匀分布,而信号的功率则集中在低频段。利用这一特性,可先用无信号功率分布的频段估计出噪声的功率谱密度,再利用其估计出噪声功率,然后将总功率减去噪声功率得到信号功率,即可求得信噪比值。
设信号带宽为B,双边功率谱密度为Ds(f),接收信号在抽样前经过了一个带宽为BLPF的低通滤波器。经过滤波器后的噪声虽然已不是严格意义上的白噪声,但在带宽BLPF范围内其功率谱密度仍然近似为常数,设为Dn(双边谱密度);接收信号的总功率为P,如图1所示。
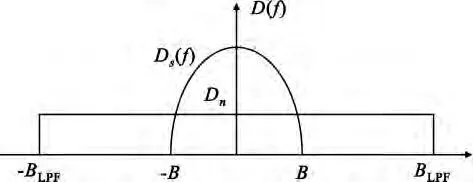
图1 接收信号功率谱示意图Fig.1 Power spectrum of receiving signals
总功率P可根据帕斯瓦尔定理从频域计算得到:
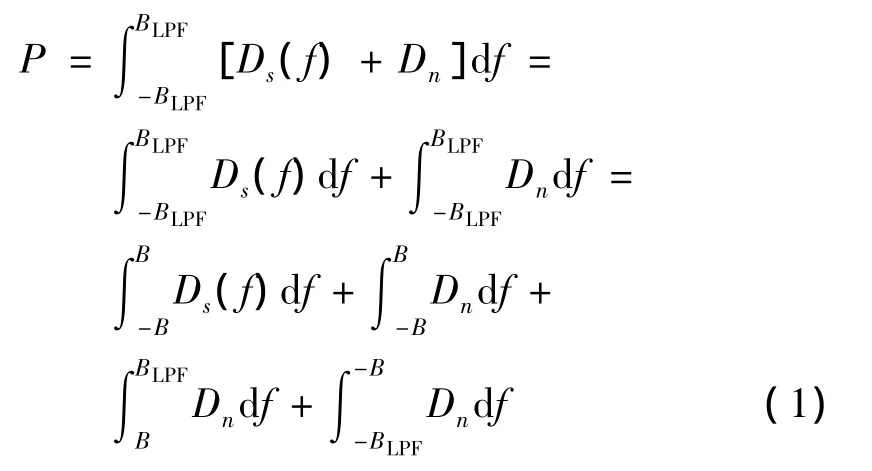
最后一个等号右边第一项为信号功率Ps,第二、三、四项之和为噪声功率Pn,总功率P和等式右边第三、四项(记为Pn1)的值都可通过DFT求取,算法的关键在于求出噪声的功率谱密度Dn。
随机信号的功率谱密度定义为
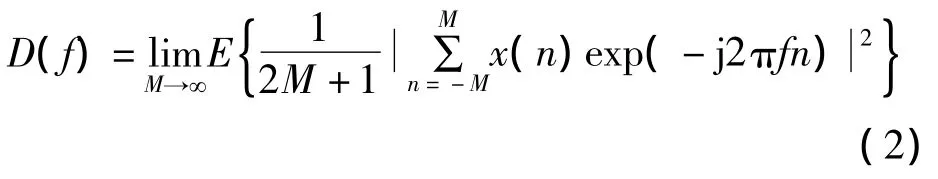
式中,E为期望运算。如果忽略期望运算并利用一组随机数据信号{x(0),x(1),…,x(N -1)}进行计算,则周期图谱估计器定义为
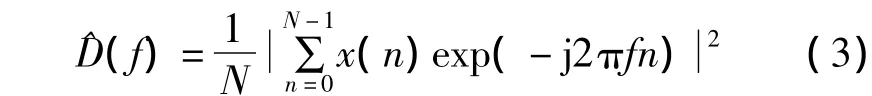
周期图在频域上的采样可用DFT求出:
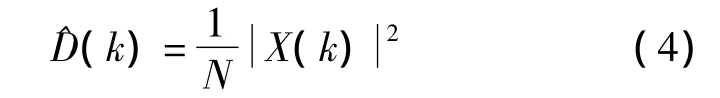
其中,X(k)是输入信号x(n)的N点DFT。信号总功率为

式(1)右边第三、四项只有噪声频段的功率为
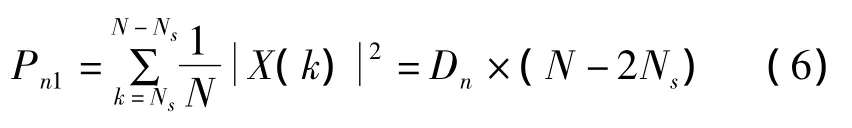
式中,Ns为信号带宽B对应的数字角频率的采样点序号:

式中,fs为采样频率,fs>2BLPF。噪声功率谱密度为
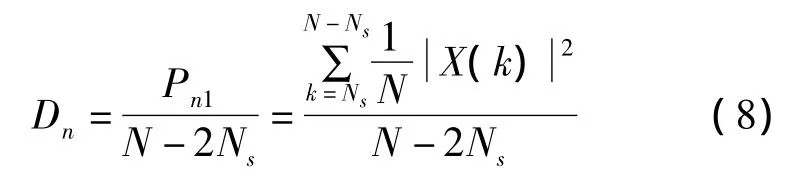
则噪声功率估计值为
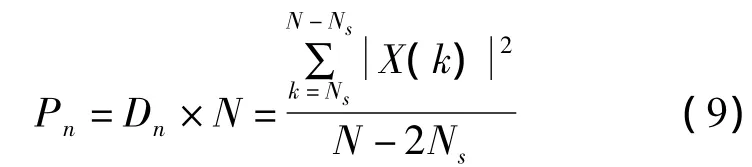
信号功率估计值为
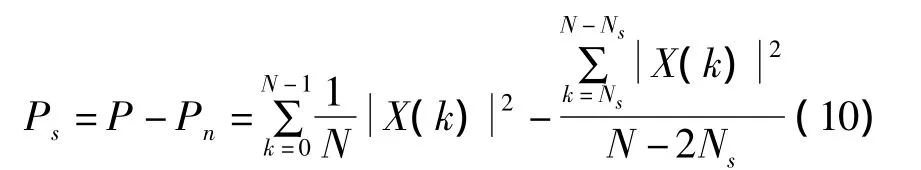
信噪比为
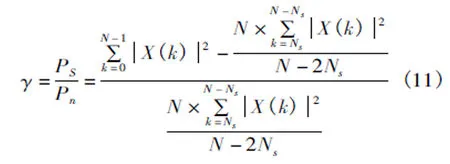
DFT运算点数N越大,通过式(8)估计得到的Dn越准确,相应信噪比的估计结果就越准确。若要进行低信噪比条件下的精确估计,需要做很大点数的DFT,这在用FPGA等方法具体实现时需要消耗大量的硬件资源;另一方面DFT的点数需要根据输入信号条件变化,实现时也不方便。
3 频域估计算法的改进
文献[12]中证明式(3)得到周期图的方差不随记录数据N的长度增大而减小,也就是说周期图不是一致估计。尽管当N→∞时均值收敛到真实的功率谱密度,但是方差并没有趋于零,原因是缺少公式(2)中的期望运算。为了改进周期图的统计特性,可以近似地用一组周期图进行平均的方法完成期望运算。假定在区间0≤n≤L-1上有K组独立记录的数据,并且都是同一随机过程的实现,若数据是{x0(n),0≤n≤L-1;x1(n),0≤n≤L-1;…;xK-1(n),0≤n≤L -1},则平均周期图估计器定义为

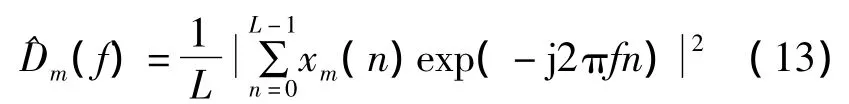
按照平均周期图估计器方案,上节中算法可做如下改进:对长度为K&N的输入序列x(n)分段进行K次 N点的 DFT,得到 K个 DFT序列 X1(k),X2(k),…,XK(k),分别求模平方后累加并求平均,得到平均周期图
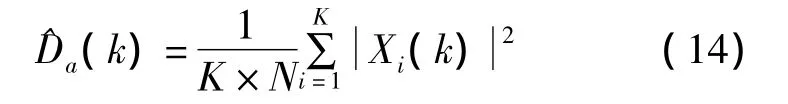

噪声功率为
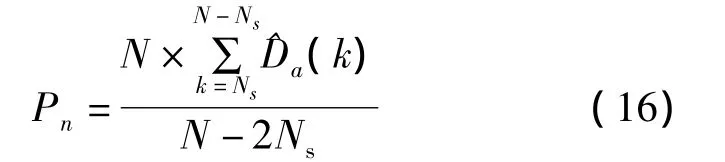
信号功率估计值
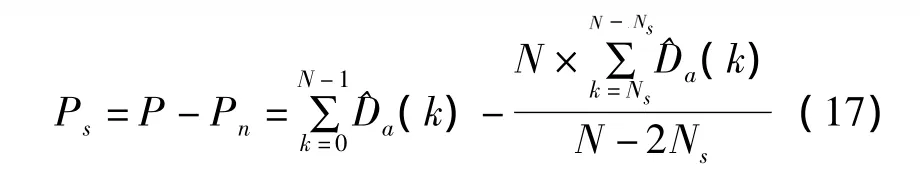
信噪比为
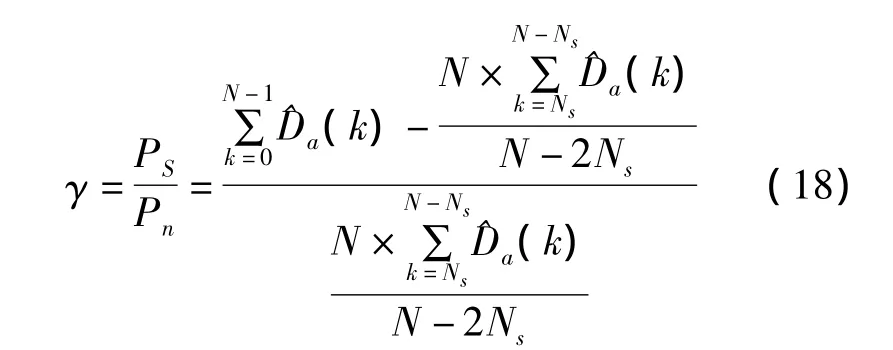
相比于之前的算法,若要进行低信噪比条件下的精确估计,该算法不需要做很大点数DFT,通过做多次DFT,将结果累积合并后再进行估计,这在用FPGA等方法实现时可以节省较多的硬件资源。
4 仿真结果及分析
仿真中信噪比估计的性能通过估计的均值和误差的均方根值来衡量。仿真中信号为BPSK信号,并经过4倍上采样后用滚降系数为0.6的根升余弦滤波器进行波形成形,最后按照信噪比要求叠加上高斯白噪声得到待进行信噪比估计的信号。其中数据速率为3 Mb/s,采样速率为12 MHz,信号带宽2.4 MHz。共进行500次仿真,最终结果为各次仿真结果的平均值。
图2和图3为只做一次DFT(即周期图法)时信噪比估计的仿真结果。图中,N为 DFT点数,即DFT计算用到的数据样值数。仿真结果表明,频域估计算法的性能随DFT计算的数据量的增加而改善,即使是在低信噪比下,也可以通过增加数据量获得需要的性能。
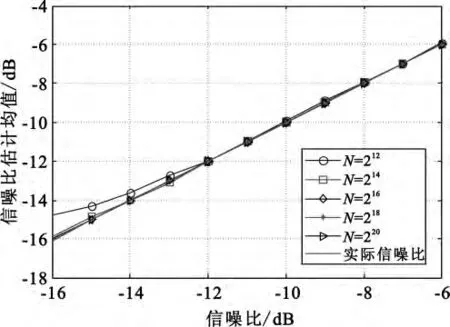
图2 信噪比估计均值Fig.2 Mean for different SNR estimation
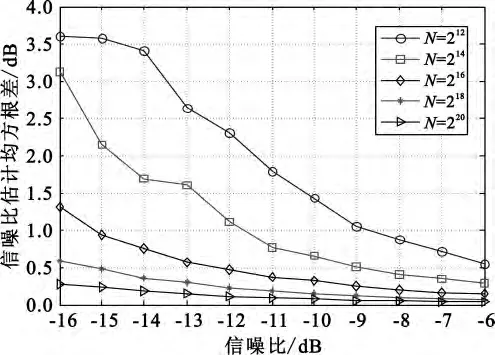
图3 信噪比估计均方根值Fig.3 RMSE for different SNR estimation
图4 和图5是采用平均周期图的方法,对多次DFT运算得到的功率谱进行平均后再进行信噪比估计的仿真结果。图中,DFT运算点数N分别为28、210、212,作为对比,图中也绘出了只做一次DFT时的估计结果,数据长度KN分别为216和220。
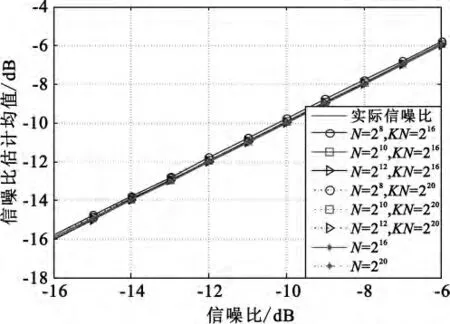
图4 改进算法信噪比估计均值Fig.4 Mean for improved algorithm
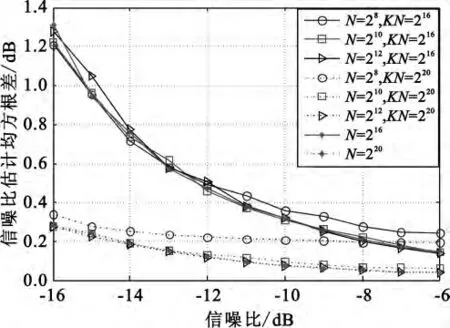
图5 改进算法信噪比估计均方根值Fig.5 RMSE for improved algorithm
从仿真结果可以看出,同等的数据量下,DFT运算点数越大,性能越好,但差别不大。当DFT点数达到210时,平均周期图估计算法的性能与只做一次DFT的估计性能基本一样,但两者复杂度却相差甚远。
下面比较两种算法的运算量,假设两种算法仿真数据长度都是220,本文算法DFT运算点数为210,那么前一种算法需要进行复数乘法运算219×20次,复数加法运算220×20次;本文算法需要进行复数乘法运算219×10次和复数加法运算220×10次。由于乘法运算所需时间较多,故以乘法运算为例,在假定情况下本文算法可以减少至少一半的运算量,有效节约了运算时间,降低了复杂度。
我们也对存在残余多普勒频移时本文的算法性能进行了仿真,结果如图6和图7所示,其中DFT的长度为210。作为对比,给出了文献[2]中的具有数据辅助的最大似然算法性能的仿真结果,仿真数据长度为216,最大多普勒频移为50 kHz。
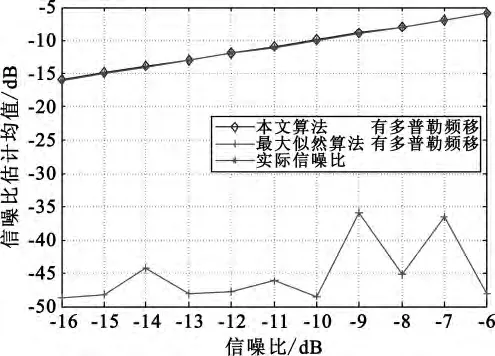
图6 不同算法信噪比估计均值Fig.6 Mean for different algorithms
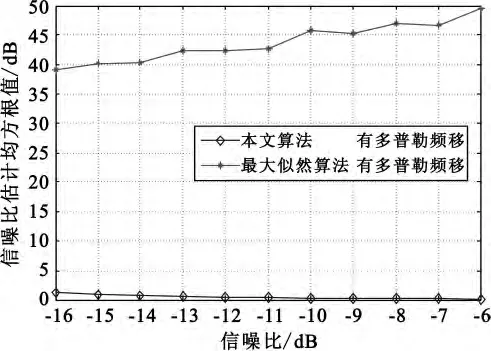
图7 不同算法信噪比估计均方根值Fig.7 RMSE for different algorithms
同样条件下,两种算法在无多普勒频移时的仿真结果如图8和图9所示。
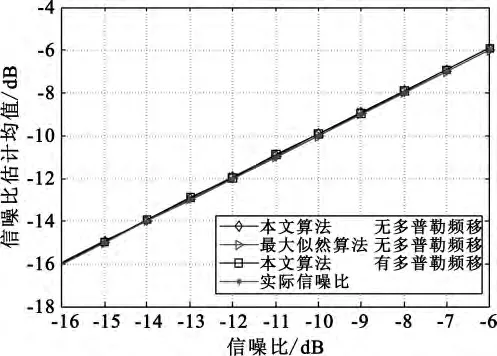
图8 不同算法信噪比估计均值Fig.8 Mean for different algorithms
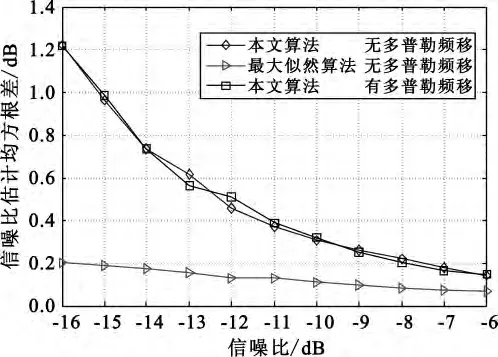
图9 不同算法信噪比估计均方根值Fig.9 RMSE for different algorithms
由图8和图9看出,无多普勒频移时信噪比值越大,两种方法估计值越接近,最大似然算法更优,但条件是需要数据辅助;同时可看出本文算法在有多普勒频移时的估计值和无多普勒频移时的估计基本一致,说明该算法不受多普勒频移影响。由图6~9可以看出最大似然算法在存在多普勒频移时,估计均值和均方根差都偏差很大,说明该算法不适用于存在多普勒频移的情况。可见,频域估计算法不仅不需要数据辅助,而且适用范围也比最大似然法更广。
5 结 论
针对已有算法出现的低信噪比下估计精度低、复杂度高、估计范围窄、适用条件有限等问题,本文首先介绍了频域信噪比估计算法,后采用平均周期图的思想给出一种新的频域估计法。该算法运算量减少,复杂度降低。仿真结果表明,该算法可以在较大信噪比范围内实现精确估计;在低信噪比条件下,随着信噪比的降低,估计精度有所下降,但可以通过适当增加数据量来实现准确估计;其适用范围广,不受残余多普勒频移的影响,与信号采用的调制方式无关。在后续研究中,我们将考虑当噪声功率谱密度不是均匀分时算法的改进。
[1]张金成,彭华,赵国庆.信噪比估计算法研究[J].信息工程大学学报,2011,12(5):535 -543.ZHANG Jin - cheng,PENG Hua,ZHAO Guo - qing.Research on SNR Estimation Algorithms[J].Journal of Information Engineering University,2011,12(5):535 -543.(in Chinese)
[2]Pauluzzi D R,Beaucieu N C.A comparsion of SNR estimation techniques for the AWGN channel[J].IEEE Transactions on Communications,2000,48(10):1681 -1694.
[3]潘申富,李振东,梁庆林.AWGN信道下PSK信号幅度与信噪比的估计[J].通信学报,2004,25(3):167-173.PAN Shen-fu,LI Zhen-dong,LIANG Qing-lin.Amplitude and SNR estimate for PSK signal in AWGN channel[J].Journal of China Institute of Communications,2004,25(3):167 -173.(in Chinese)
[4]许华,王爱粉,杨晓宇.常规数字通信信号信噪比估计综述[J].信号处理,2013,29(6):723-733.XU Hua,WANG Ai- fen,YANG Xiao - yu.Survey of the SNR Estimation of Conventional Digital Communication Signals[J].Journal of Signal Processing,2013,29(6):723 -733.(in Chinese)
[5]Ren G L,Chang Y L,Zhang H.A new SNR’s estimator for QPSK Modulations in an AWGN Channel[J].IEEE Transactions on Circuits and SystemsⅡ,2005,52(6):336-338.
[6]杜瑜.一种基于矩特性的SNR估计方法[J].电讯技术,2008,48(8):102 -104.DU Yu.A SNR Estimation Method Based on Moments[J].Telecommunication Engineering,2008,48(8):102-104.(in Chinese)
[7]Mosquera C,Lopez-valcarce R,Alvarez-diaz M.SNR Estimation for Multilevel Constellations Using Higher-Order Moments[J].IEEE Transactions on Signal Processing,2010,58(3):1515 -1526.
[8]许华,樊龙飞,郑辉.一种精确的QPSK信号信噪比估计算法[J].通信学报,2004,25(2):55-60.XU Hua,FAN Long - fei,ZHENG Hui.A precise SNR estimation algorithm for QPSK signals[J].Journal on Communications,2004,25(2):55 -60.(in Chinese)
[9]叶淦华,张邦宁,陆锐敏.基于曲线拟合的信噪比估计校正方法[J].电讯技术,2007,47(5):86-88.YE Gan-hua,ZHANG Bang- ning,LU Rui- min.Revised SNR Estimator Based on Curve Fitting[J].Journal of Telecommunication Engineering,2007,47(5):86 -88.(in Chinese)
[10]Morelli M,Moretti M,Imbarlina G,et al.Low complexity SNR estimation for transmissions over time-varying flat- fading channels[C]//Proceedings of 2009 Wireless Communications and Networking Conference.Budapest:IEEE,2009:1 -4.
[11]Kosinski J,Su W,Shi Y Q,et al.An investigation of non-data-aided SNR estimation techniques for analog modulation signals[C]//Proceedings of 2010 IEEE Sarnoff Symposium.Princeton,NJ:IEEE,2010:1 -5.
[12]Kay S M.现代谱估计:原理与应用[M].黄建国,武延祥,杨世兴,译.北京:科学出版社,1994:48-58.Kay S M.Modern Spectral Estimation:theory and application[M].Translated by HUANG Jian-guo,WU Yan- xiang,YANG Shi- xing.Beijing:Science Press,1994:48 -58.(in Chinese)

