双模噪声背景下自适应小波阈值去噪*

刘 伟，山拜·达拉拜

(新疆大学 信息科学与工程学院，乌鲁木齐830046)

1 引 言

信号去噪问题一直是一个重要而热门的课题，现在已有多种信号去噪的方法，如维纳(Wiener)滤波法、卡尔曼(Kalman)滤波法、减谱法等。小波阈值去噪方法是D.L.Donoho［1－2］在1995年提出的一种简单有效的去噪方法，由于此方法在Besov 空间上可得到最佳估计值，而线性估计达不到同样的结果，因此引起了学者的广泛关注。

目前学术界对于小波阈值去噪已有较多的研究。文献［3］研究发现经过小波分解后，不同分解层的系数对信号和噪声的比例分布有所不同，利用这一特性改进阈值选取，与传统阈值相比，图像增强过程中减少了噪声残留和误判。文献［4］利用平移不变量小波阈值去噪算法，使阈值的变化与噪声的小波变换随尺度的变化特性相一致，以期改善去噪效果。文献［5］总结了具有代表性的4 种改进小波阈值去噪法，通过仿真将各方法去噪结果进行对比，得到两个重要结论:在相同实验条件下，改进的阈值法并不绝对优于硬、软阈值法;很难找到一种在任何实验条件下都绝对优越的阈值去噪法。文献［6］用高斯混合模型来近似小波系数广义高斯分布，估计出高斯混合分布的各部分方差，并选择最小的方差参数作为噪声方差估计，这种方法在噪声方差较小时去噪效果较好。

这些研究都是假设以高斯噪声为背景［7］，在简单的电子设备中这是合适的。实际设备非常复杂，再加上各种各样外界的干扰，这种假设不能满足要求。

本文以双模噪声为研究背景，拓展了小波阈值去噪法的应用;从数学上分析了经典算法的缺点，设计了改进的阈值函数和控制函数，克服了经典算法不足的同时具有信噪比寻优能力。仿真结果表明，该算法是一种性能优异的去噪算法。

2 双模噪声的数学模型和数字特征

双模噪声是由两种噪声叠加成的简单混合噪声，比高斯噪声更具一般性，双模过程主要有3 种模型。

模型1［8］高斯过程g(t)叠加随机均匀相位振荡过程Bcos(t)，其概率密度函数、均值和方差分别为

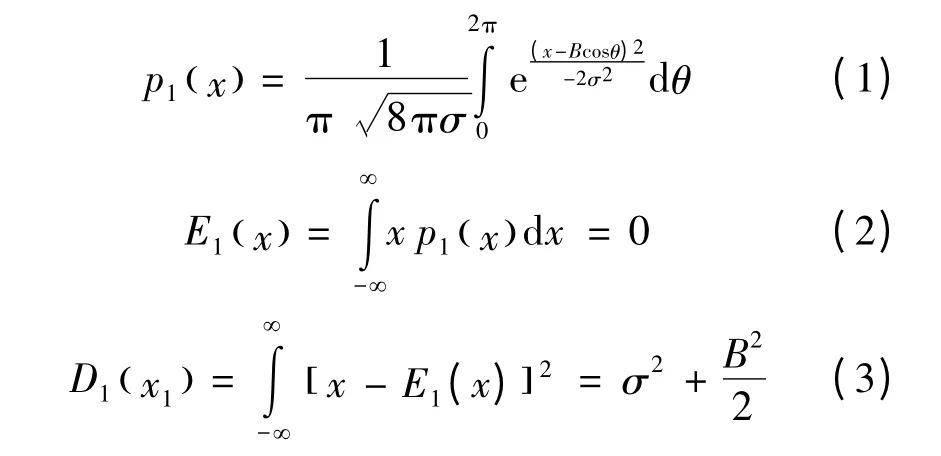
其中，σ2是高斯分量的方差。

模型2 高斯过程g(t)叠加码间干扰过程，b ( t)= ±b，其概率密度函数、均值和方差分别为

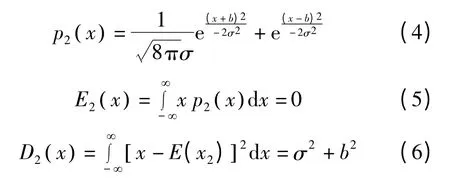
模型3 当b ＞2σ2，模型3 与模型2 等价，概率密度函数为

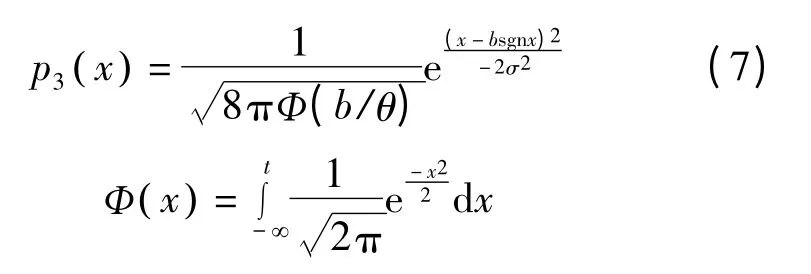
其中，Φ(x)为标准正态分布函数，sgn 为符号函数。

3 小波阈值去噪

3.1 去噪原理

在信号处理中，信号经过离散小波变换后［9］，属于Besov 空间的信号的能量主要集中在小波域内有限的几个系数中，而噪声的能量却分布于整个小波域内。因此，经小波分解后信号的小波系数要大于噪声的小波系数，可以选择一个合适的阈值对小波系数进行阈值处理，就可以把信号系数保留下来(硬阈值法)或将其进行收缩(软阈值法)，而使大部分的噪声系数置为零，从而达到去噪的目的。假设一维观测信号f(t)=h(t)+n(t)，其中，h(t)为原始信号，n(t)是式(1)描述的双模噪声。若用W(·)、W(·)－1分别表示离散小波变换和离散小波逆变换，用D(·，λ)表示对小波系数阈值处理，那么在含噪信号f(t)中恢复原始信号的估计值(t)可概括为以下三步:Y = W(f)，R = D(Y，λ)，() t =W(R)－1。

3.2 阈值函数

经典算法的阈值函数有硬阈值函数和软阈值函数。

硬阈值函数:

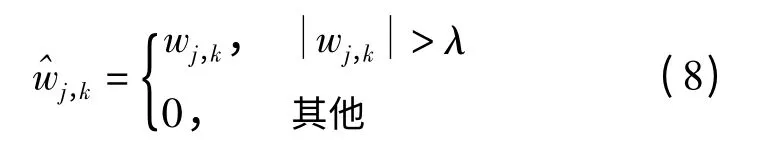
软阈值函数:

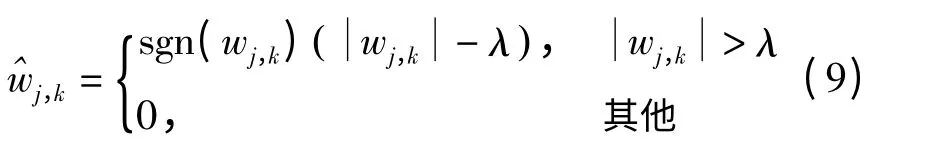
式(8)、(9)中，λ 为阈值，wj，k为小波系数，为处理后的小波系数。

硬、软阈值函数如图1所示。

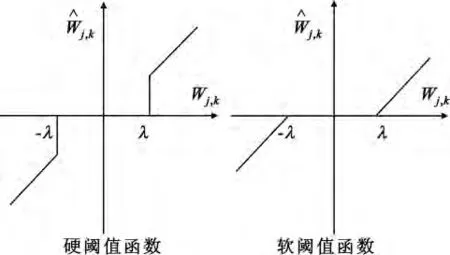
图1 硬、软阈值函数Fig.1 Hard and soft threshold functions

硬阈值函数不连续，对数据变化反应过为灵敏，在重构信号时会产生振荡。软阈值函数将绝对值大于阈值的小波系数进行收缩处理，有可能造成高频信息的损失，其连续性较好，但小波系数真实值与估计值存在恒定误差，在重构信号时影响逼近程度。

改进的阈值函数:

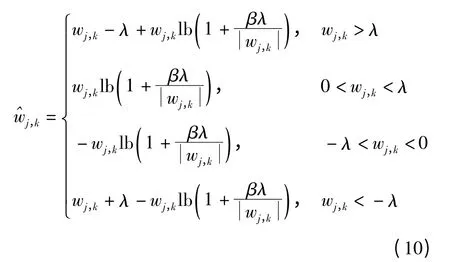
式(10)中β∈［0，1］为控制因子，用于控制函数的形状，即控制函数曲线的衰减程度，β 越小衰减越严重;当β=0 时，新阈值函数等于软阈值函数。

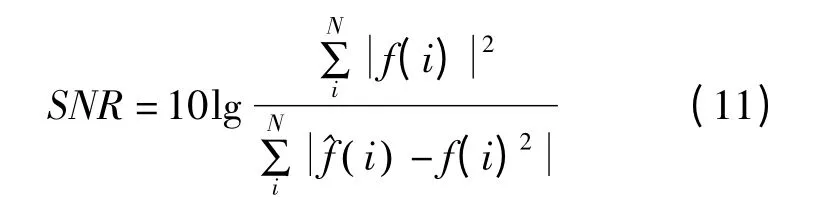
分析图2可以得出，改进阈值函数在硬、软阈值函数之间存在一个平滑过渡的区域，函数连续性更好，恒定误差小于软阈值函数。函数曲线随β 的增大，在硬、软阈值函数曲线范围内移动，β 越大，越靠近硬阈值函数曲线。

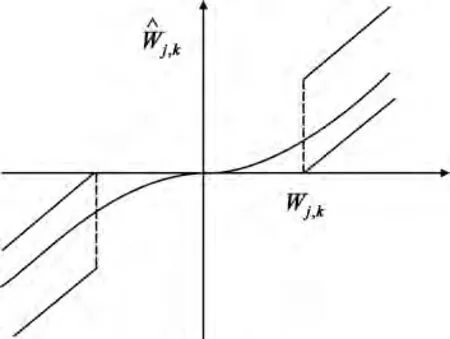
图2 改进的阈值函数Fig.2 Improved threshold function

小波阈值的选取很重要。如果阈值太小，那么阈值处理后的小波系数中包含了过多的噪声分量;如果阈值太大，那么将会丢失信号的部分有用信息，从而造成重构信号失真。1994年Donohue 和Johnstone 推导出了计算阈值的通用公式:

式中，N 是信号长度，σ 为噪声标准差。式(12)称为全局阈值，它是在高斯噪声的模型上提出的，在非高斯噪声的情况下，按照不同的分解尺度采用不同的阈值λ。

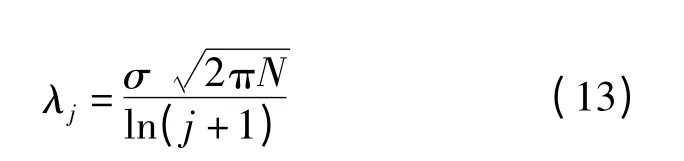
3.3 去噪过程

(1)选择小波基:小波基一般根据信号的特性来选择，确定分解的层数;

(2)小波分解:对信号进行小波分解。进行等间隔抽样，然后对抽样序列进行离散小波变换，得到小波的展开系数;

(3)阈值处理:对每层系数选择一个阈值，并且对高频系数进行阈值量化处理;

(4)信号重构:用小波分解的低频系数和经过处理过的各层高频系数进行小波逆变换，得到原始信号的估计值。

3.4 自适应小波阈值去噪

自适应去噪过程如图3所示。

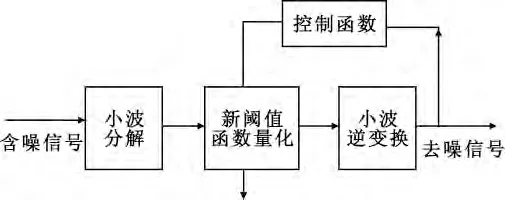
图3 自适应去噪过程Fig.3 The adaptive denoising process

由测试样本得到控制函数y =f(β)曲线，分析图4可知:当β∈［0，0.5］时，函数曲线随β 的增大而增大;当β = 0. 5 时，函数达到最大值y－max=37.356 2;当β∈［0.5，1］时，函数曲线随β 的增大而减小，减小曲线比增大曲线平滑，根据图4构造控制函数

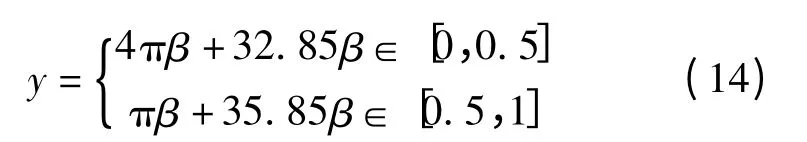
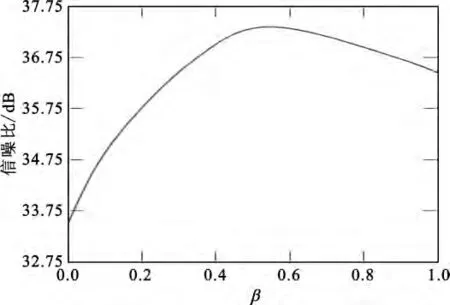
图4 函数y=f(β)曲线Fig.4 The curve of function y=f(β)

算法步骤描述如下:

(1)初始化参数，令β =0、i =1，λ 由式(13)确定，设置迭代次数i－max;

(2)判断i ＞i－max是否成立，YES 则算法结束，NO 则i=i+1 返回步骤3;

(3)对含噪信号进行自适应去噪处理，处理过程如图3所示;

(4)判断β ＞1 是否成立，YES 则算法结束，NO则β=β+0.01，返回步骤2。

算法流程图如图5所示。

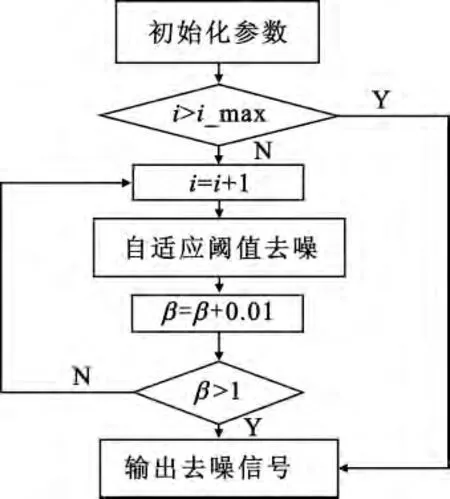
图5 算法流程图Fig.5 Flow chart of the proposed algorithm

4 仿真实验

仿真实验在Matlab 2012a 平台进行，双模噪声模型为模型1，用高斯白噪声叠加随机振荡信号产生，随机振荡信号幅值不能太大，否则会影响heavy sine 形状。Coiflet 小波消失矩大，对称性好，小波分解层数兼顾去噪效果和实验对比，选择coif3 小波进行5 层分解。B =4 的双模噪声作为测试样本用于构造控制函数，B=2 的双模噪声作为实验样本进行去噪实验。3 种去噪方法各实验50 次，heavy sine去噪前信噪比为19.001 8 dB。

图6是含噪信号图形，图7～9分别是硬阈值法、软阈值法、自适应小波阈值算法的去噪图形曲线，表1是3 种方法的信噪比(dB)。

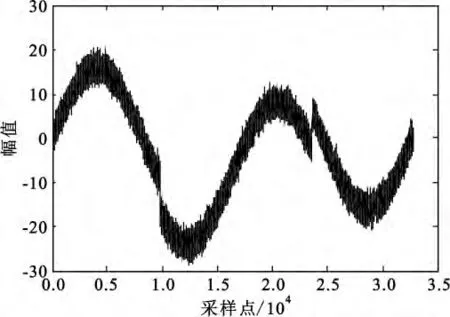
图6 含噪信号Fig.6 Signal with niose

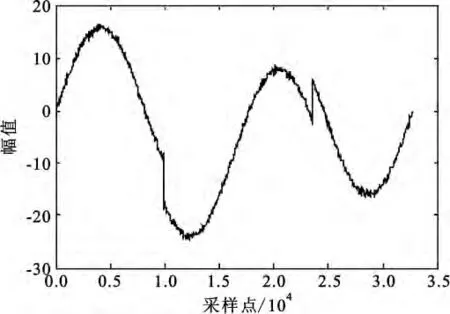
图7 硬阈值法去噪曲线Fig.7 Denoising result by hard threshold method

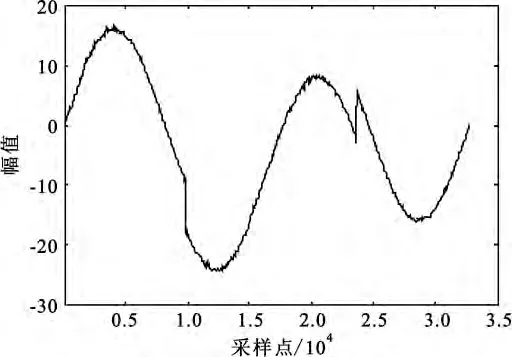
图8 软阈值法去噪曲线Fig.8 Denoising result by soft threshold method

图9 自适应小波阈值算法去噪曲线Fig.9 Denoising result by adaptive wavelet threshold algorithm

分析图6～9可知硬、软阈值法去噪结果不清晰，比较粗糙;自适应小波阈值算法去噪结果清晰、光滑，更好地抑制了噪声信号。分析表1可知，新算法信噪比相对硬、软阈值法分别提高9 dB和4 dB。

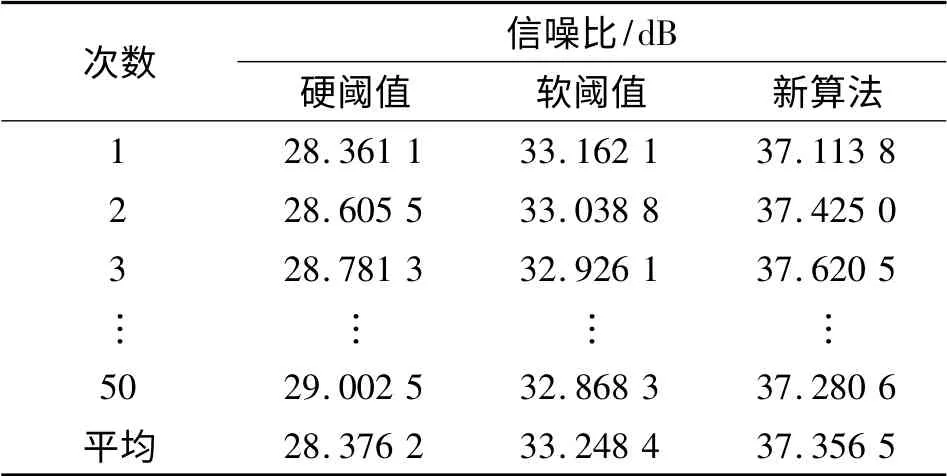
表1 3 种方法的信噪比Table1 The signal－to－noise ratio of three methods

5 结 语

综上所述，本文在双模噪声背景下提出一种自适应小波阈值算法，实验结果表明该算法具有自适应性强、算法简单、去噪效果好等特点。但是，这只是在一种双模噪声模型下进行的仿真，如何建立一种通用的算法仍需要研究。再者，如何根据要求快速准确地自适应确定阈值参数λ 可作为下一步着手进行的工作。

［1］ Donoho D L. De－noising by soft－thresholding［J］. IEEE Transactions on Information Theory，1995，41(3):613－627.

［2］ Zhao S P，Li X W，Xing J H，et al. An Wavelet Image Automatic Threshold Selection Denoising Method［J］.Advanced Materials Research，2012，482(7):780－783.

［3］ You F，Zhang Y. Research of an Improved Wavelet Threshold Denoising Method for Transformer Partial Discharge Signal［J］. Journal of Multimedia，2013，8(1):130－132.

［4］ 程忠良，贾振红，覃锡忠，等. 基于改进阈值的低压电力线信道中的小波去噪方法［J］. 电讯技术，2009，49(8):18－22.CHENG Zhong－liang，JIA Zhen－hong，QIN Xi－zhong，et al. Based on the improved threshold of wavelet denoising method of low voltage power line channel［J］. Telecommunications Engineering，2009，49(8):18－22.(in Chinese)

［5］ 王拴中，朱玉田. 改进小波阈值去噪法的对比性仿真实验与分析［J］. 噪声与振动控制，2012，32(1):128－132.WANG Shuan－zhong，ZHU Yu－tian. Improved wavelet threshold denoising method of simulation experiment and comparative analysis［J］. Journal of Noise and Vibration Control，2012，32(1):128－132.(in Chinese)

［6］ 曲巍崴，高峰. 基于噪声方差估计的小波阈值降噪研究［J］. 机械工程学报，2010(2):28－33.QU Wei－wei，GAO Feng. Based on noise variance estimation in wavelet threshold denoising study［J］. Journal of Mechanical Engineering，2010(2):28－33.(in Chinese)

［7］ Guo D，Wu Y，Shamai S，et al. Estimation in Gaussian noise:Properties of the minimum mean－ square error［J］. IEEE Transactions on Information Theory，2011，57(4):2371－2385.

［8］ 李世军，山拜·达拉拜，金永强. 高斯型混合双多模噪声模型分析［J］. 电讯技术，2005，45(3):55－58.LI Shi－jun，Senbai Dalabaev，JIN Yong－qiang. Double multimode gaussian mixture noise model analysis［J］.Telecommunications Engineering，2005，45(3):55－58.(in Chinese)

［9］ Demirel H，Anbarjafari G. Image resolution enhancement by using discrete and stationary wavelet decomposition［J］. IEEE Transactions on Image Processing，2011，20(5):1458－1460.