AZ61镁合金的热压缩变形行为及组织演变
张 蓉,罗 裴(1.湖南工学院机械工程学院,衡阳 4100;.湖南科技经贸职业学院机电工程学院,衡阳 41001)
0 引 言
镁合金具有比强度和比刚度高、导热性和阻尼减振性能好、电磁屏蔽性能和机加工性能优异等特点,在航天航空、汽车、电器、通讯等领域具有广阔的应用前景[1]。镁合金属于密排六方结构金属,独立的滑移系较少,塑性加工成形比较困难[2]。到目前为止,镁合金制品主要通过压铸的方法生产,而铸造产品的显微组织和第二相粗大,且存在较多气孔和缩孔等缺陷,难以满足高性能结构材料的性能要求,这极大地限制了镁合金的广泛应用[3]。大量研究表明[4],镁合金在热变形过程中极易发生动态再结晶使晶粒得以细化,同时热变形过程中的金属流动还可以使气孔和缩孔等缺陷得以消除,从而大幅提高了合金的综合力学性能。此外,通过改变变形工艺参数还可以控制合金的显微组织,以获得不同的力学性能,从而满足不同服役条件下的性能要求。因此,镁合金热塑性变形的研究逐渐成为了国内外研究的重点。
热模拟技术可为合理制定材料热加工工艺提供有效依据,是材料热加工研究的重要手段,该技术已在镁合金热塑性变形中得到了广泛应用[5]。目前,国内 外 相 关 研 究 主 要 集 中 在 AZ31[6]、AZ91[7]和ZK60[8]等合金上,而有关AZ61镁合金热模拟研究的报道较少[9]。鉴于此,作者以AZ61镁合金为研究对象,在250~450℃和0.001~10s-1应变速率范围内对其进行高温热压缩变形模拟试验,研究了应变速率和变形温度对流变应力和显微组织的影响规律,确定了合金热变形的塑性变形本构方程,期望能对合理制定AZ61镁合金热塑性加工工艺起到一定的指导作用。
1 试样制备与试验方法
试验用材料为AZ61镁合金,其名义成分(质量分数)为 Mg-6.3%Al-1.1%Zn-0.2%Mn。在中频感应炉中熔炼,铸坯经400℃均匀化处理20h,合金平均晶粒尺寸约为150μm;将均匀化后的铸坯加工成尺寸为φ10mm×15mm的试样,并在试样两个端面分别加工出0.2mm深的凹槽,用于涂敷石墨和机油的混合物,以减小试样与压头之间的摩擦;然后在Gleeble-1500型热模拟试验机上进行热压缩试验,压缩温度为250~400℃,应变速率为0.001~10s-1,加热速率为200℃·min-1,压缩前试样在变形温度下保温3min,压缩变形量为50%,即真应变为0.69。变形完成后立即对试样进行水淬,以保留高温变形组织。
取垂直于压缩方向的面在Olympus光学显微镜下进行组织观察,腐蚀剂由50mL无水乙醇、20mL冰醋酸、20mL蒸馏水和5g苦味酸组成;采用面积法和截线法分别对再结晶程度和再结晶晶粒尺寸进行测量。
2 试验结果与讨论
2.1 流变曲线
从图1中可以看出,合金在不同变形条件下的真应力-真应变曲线都表现出了明显的动态再结晶特征。在变形初期,加工硬化占主导,其硬化作用远超过动态回复或动态再结晶引起的软化作用,应力迅速上升;随着变形量增加,合金中的位错密度升高,动态回复和动态再结晶加快,软化作用增强,加工硬化作用逐渐被软化作用抵消,从而导致应力上升的速度明显减慢;当加工硬化和动态再结晶软化达到平衡时,流变应力达到峰值;当应变超过一定值后,动态再结晶程度进一步增大,流变应力持续下降,最后达到一稳定值。
从图1(a)可以看出,在同一变形温度下,应变速率越大,合金的峰值应力越高,峰值应力对应的应变量越大。随着应变速率的增大,合金完成变形的时间缩短,位错滑移和攀移的有效时间缩短,这在一定程度上抑制了动态再结晶的软化作用,从而使峰值应力增大,并且使得动态再结晶软化和应变硬化达到平衡的应变量增大[9]。从图1(b)可以看出,在同一应变速率下,变形温度越高,峰值应力越低,峰值应力所对应的应变量越小。随着变形温度升高,一方面,滑移系启动的临界切应力下降,导致镁合金的变形抗力降低;另一方面,位错的交滑移、攀移以及亚晶的形成、合并更容易进行,促进了动态再结晶的发生,从而使动态再结晶软化和应变硬化达到平衡的应变量减小[10]。
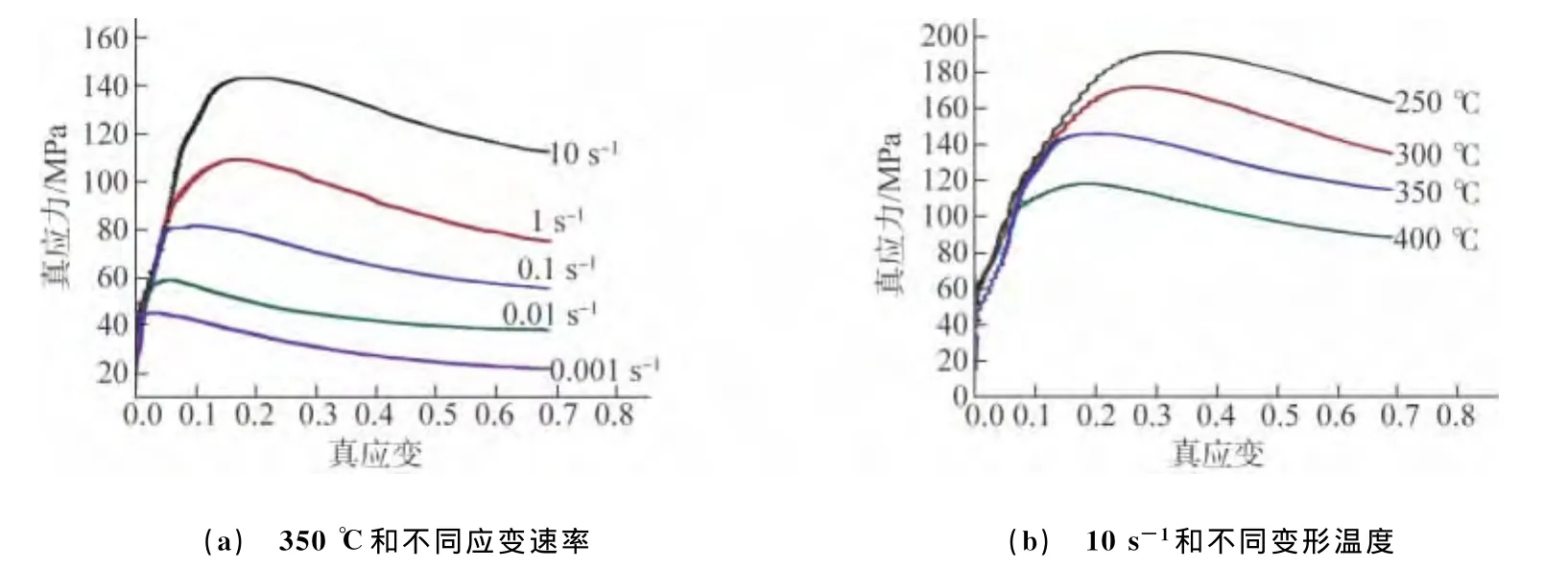
图1 AZ61镁合金在不同变形条件下的真应力-真应变曲线Fig.1 True stress-true strain curves of AZ61magnesium alloy compressed under different conditions:(a)at 350 ℃and different strain rates and(b)at strain rate of 10s-1 and different temperatures
2.2 本构方程
金属材料在热变形过程中,流变应力σ主要取决于变形温度T和应变速率˙ε。不同合金材料的热加工研究表明,在较低的应力水平下,材料的流变应力和应变速率之间的关系可用指数关系描述[11]:

式中:n1和A1为材料常数。
在较高的应力水平下,材料的流变应力和应变速率之间的关系可用幂指数关系描述:

式中:β和A2为材料常数。
Sellars和Tegart在综合指数关系和幂指数关系方程局限性的基础上,提出了用包含变形激活能Q和变形温度T的双曲线正弦形式修正的Arrhenius关系曲线来描述流变应力与应变速率之间的关系[12]:

式中:n,α和A 为材料常数,并且α=β/n1;R 为气体常数;Z为Zener-Hollomon参数。
在低应力水平下式(3)接近式(1),在高应力水平下式(3)接近式(2),因此式(3)可适用于整个应力范围。对式(1)~ (3)进行变形,分别可以得到以下关系式:

金属的流变应力通常由单向压缩或拉伸时的屈服应力、峰值应力或稳态应力来衡量,易发生动态再结晶的材料通常选用峰值应力。由于镁合金层错能低,易发生动态再结晶,因此,选用峰值应力来衡量流变应力。图2所示为AZ61合金热压缩变形时峰值应力与应变速率的幂指数和指数关系,其斜率分别为β和n1。由图2可得β=0.091,n1=8.823,经优化处理后α取值为0.01。
对式(3)求偏微分可得热变形激活能Q为:
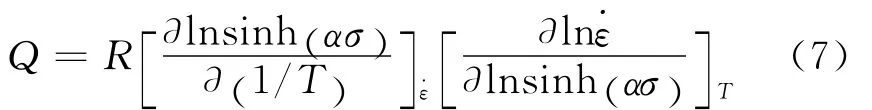
式(7)中的第一个偏微分为图3(b)中1 000/T-lnsinh(ασ)的斜率,第二个偏微分为图 3(a)中lnsinh(ασ)-ln˙ε的斜率。通过拟合可以计算出合金的热变形激活能Q为147.262kJ·mol-1,其大于镁合金的自扩散激活能Qsd(135kJ·mol-1)。由此可见,热激活控制的动态再结晶是AZ61合金热压缩变形软化的主要机制[13]。
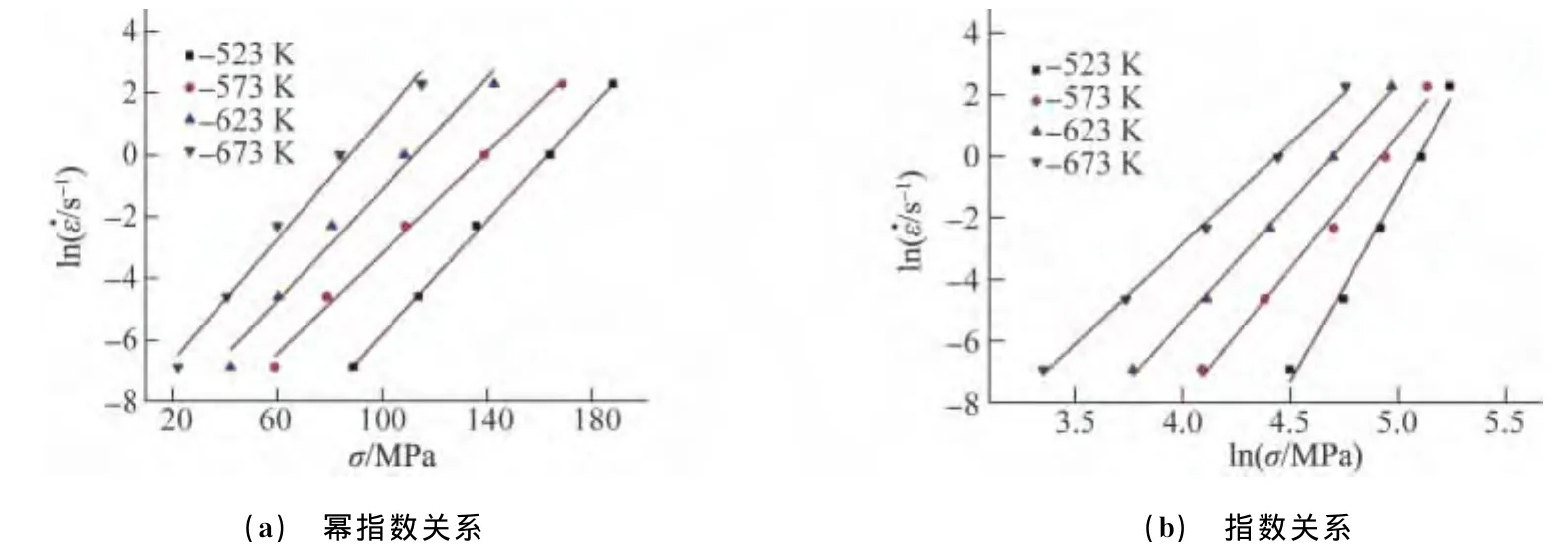
图2 AZ61合金峰值应力与应变速率的关系Fig.2 Relationship between peak stress and strain rate:(a)power law and(b)exponential law
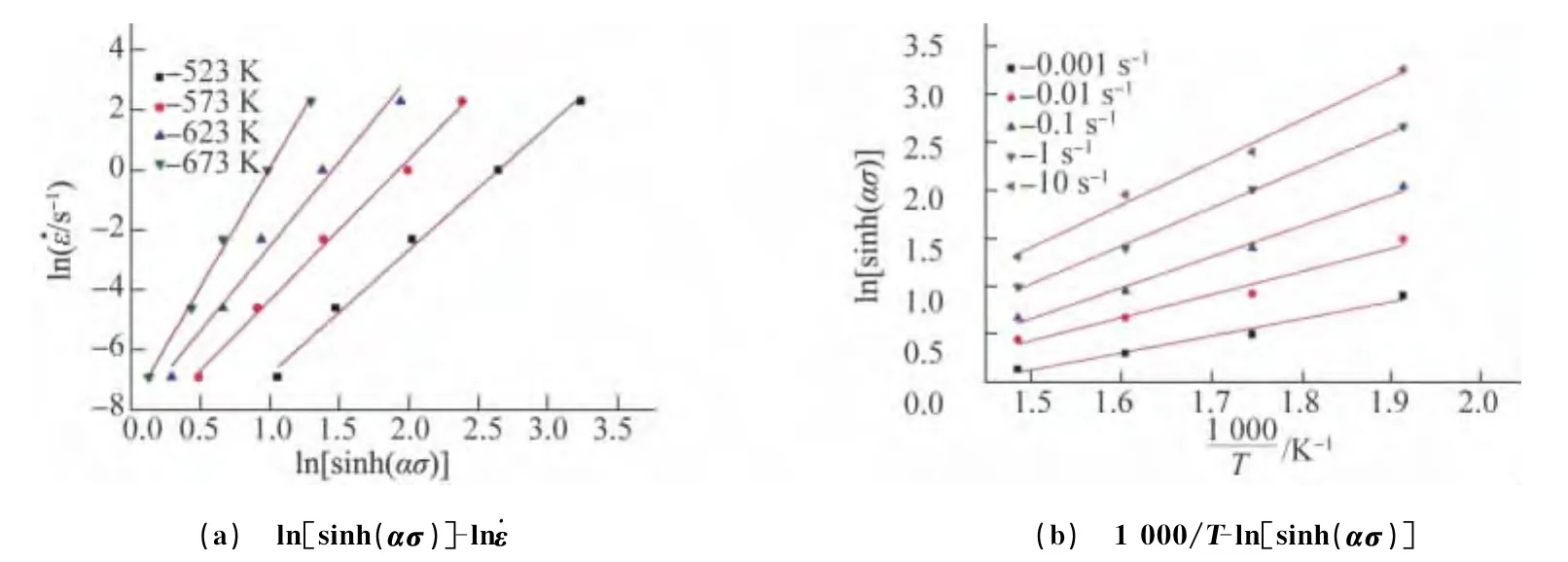
图3 本构方程的标准分析图Fig.3 The standard analysis of the constitutive equation
将材料参数α和Q分别代入式(6),得到Z参数与峰值应力之间的关系式,曲线如图4所示。对关系曲线进行线性回归,可以发现峰值应力双曲正弦项的自然对数与Z参数的自然对数满足良好的线性关系,其相关系数为0.987,由此进一步说明了合金压缩变形的流变应力与应变速率及变形温度之间的关系可用Arrhenius关系曲线来描述。通过拟合得到A=1.367×109,n=5.096,将α,Q,A 和n代入式(3)得到AZ61镁合金高温塑性变形的本构方程为:

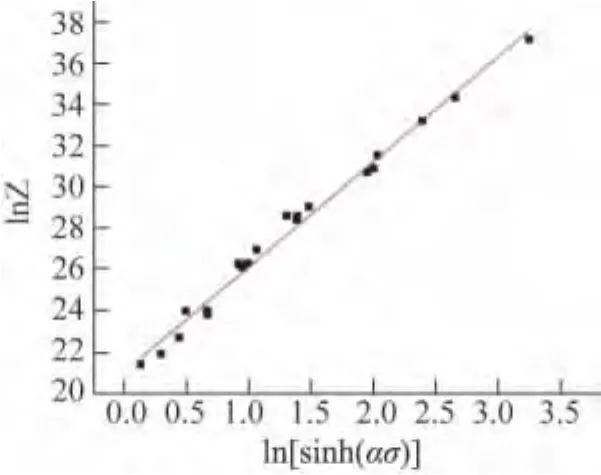
图4 lnZ与ln[sinh(ασ)]之间的关系曲线Fig.4 lnZvs ln[sinh(ασ)]
2.3 显微组织
应变速率为0.001s-1时,初始晶界上形成了项链状细小的再结晶组织,同时在初始晶粒内有少量孪晶,如图5(a)所示;随着应变速率的增加,初始晶界附近项链状再结晶组织的晶粒尺寸有所长大,初始晶粒内的孪晶密度升高,如图5(b),(c)所示;当应变速率增加到10s-1时,初始晶粒内的孪晶密度明显升高,再结晶同时在初始晶界和孪晶上启动,合金再结晶程度大幅提高。由于镁合金为密排六方结构金属,缺少足够的独立滑移系,孪生在塑性变形过程中发挥着重要作用,特别是在高应变速率的变形条件下,位错滑移等速度控制机制将受到抑制,孪生协调变形作用显著增强[14]。因此,随着应变速率的增加,孪晶的密度明显增大。孪晶界与晶界一样可以阻碍位错运动,为再结晶提供储能,促进再结晶在孪晶上形核[15]。因此,镁合金在高应变速率下压缩变形时可以获得比低应变速率下更高的再结晶程度。

图5 AZ61镁合金在250℃和不同应变速率下压缩变形后的显微组织Fig.5 Microstructure of AZ61magnesium alloy compressed at 250 ℃ and different strain rates
从图6中可以看出,随着变形温度的升高,初始晶粒内的孪晶密度下降;当变形温度升高到350℃时,合金组织中基本没有观察到孪晶。这是由于随着变形温度的升高,非基面滑移开始启动,参与滑移的滑移系数量增多,降低了孪生在塑性变形中的作用。此外,从图中还可以看出,随着变形温度的升高,再结晶程度和再结晶晶粒尺寸明显增大。变形温度为250℃时,合金再结晶程度为20%,再结晶晶粒尺寸为4μm;变形温度升高到400℃时,合金基本完全再结晶,再结晶晶粒尺寸为12μm。这是由于随着温度升高,位错的交滑移、攀移以及亚晶的形成、合并更容易进行,促进了动态再结晶的发生,从而使合金的再结晶程度增大;同时由于晶界扩散和迁移的能力随温度的升高而增强,晶粒容易长大,从而导致再结晶晶粒尺寸增大[16]。

图6 AZ61镁合金在应变速率为10s-1和不同变形温度下压缩后的显微组织Fig.6 Microstructure of AZ61magnesium alloy compressed at strain rate of 10s-1 and different temperatures
3 结 论
(1)AZ61镁合金的热压缩变形行为可用Arrhenius关系曲线来表示,其高温塑性变形本构方程为:Z =1.367×109[sinh(0.01σ)]5.096。
(2)在同一变形温度下,合金的再结晶程度随应变速率的增加而增大;在0.001~1s-1的低应变速率下变形时,再结晶主要发生在初始晶界上;在高应变速率10s-1下变形时,再结晶在初始晶界和孪晶上启动,获得了比低应变速率变形条件下更为均匀的再结晶组织。
(3)在同一应变速率下,再结晶程度和再结晶晶粒尺寸随变形温度的升高而增大;应变速率为10s-1时,合金在250℃压缩变形时的再结晶程度和平均晶粒尺寸分别为20%和4μm,变形温度升高到400℃时,合金的再结晶程度和平均晶粒尺寸分别增加至100%和12μm。
[1]黎文献.镁及镁合金[M].长沙:中南大学出版社,2005.
[2]AVEDESIAN MM,BAKER H.ASMspecialty handbook:magnesium and magnesium alloys[M].Materials Park:ASMInternational,1999.
[3]KAINER K U.Magnesium alloys and technology[M].Weinheim:GKSS Research Center Geesthacht GmbH,2003.
[4]陈振华.变形镁合金[M].北京:化学工业出版社,2005.
[5]肖梅,周正,黄光杰,等.AZ31镁合金热变形行为及加工图[J].机械工程材料,2010,34(4):18-21.
[6]孙述利,张敏刚,周俊琪,等.AZ31镁合金在热压缩过程中的变形行为[J].机械工程材料,2010,34(8):88-90.
[7]肖心萍,于彦龙,王亚楠.AZ91镁合金的热压缩变形行为及晶粒细化[J].机械工程材料,2011,35(5):93-95.
[8]毛建军,潘复生,陈先华,等.ZK60镁合金的热压缩变形行为[J].材料导报,2010,24(2):58-62.
[9]王少楠,唐国翌,傅万堂,等.铸态AZ61镁合金热压缩变形组织变化[J].材料热处理学报,2009,30(5):39-43.
[10]MYSHLYAEV MM,MCQUEEN H J,MWEMBELA A,et al.Twinning,dynamic recovery and recrystallization in hot worked Mg-Al-Zn alloy[J].Science and Engineering:A,2002,337:121-131.
[11]SLOOFF F A,ZHOU J,DUSZCZYK J,et al.Constitutive analysis of wrought magnesium alloy Mg-AL4-Znl[J].Scripta Materialia,2007,57(8):759-762.
[12]MCQUEEN H J,RYAN N D.Constitutive analysis in hot working[J].Materials Science and Engineering:A,2002,322(1/2):43-63.
[13]MOREAU G,CORNET J A,CALAIS D.Acceleration de la diffusion chimique sous irradiation dans le systeme alumin-ium-magnesium[J].Journal of Nuclear Materials,1971,38(2):197-202.
[14]WU Y Z,YAN H G,CHEN J H,et al.Hot deformation behavior and microstructure evolution of ZK21magnesium alloy[J].Materials Science and Engineering:A,2010,527:3670-3675.
[15]YIN D L,ZHANG K F,WANG G F,et al.Warm deformation behavior of hot rolled AZ31Mg alloy[J].Materials Science and Engineering:A,2007,392:320-325.
[16]陈振华,许芳艳,傅定发,等.镁合金的动态再结晶[J].化工进展,2006,25(2):140-146.

