顾及空间异质性的多尺度空间负荷预测

赵 强 ，景 罗 ，赵光俊 ，刘二涛

（1.华北电力大学 控制与计算机工程学院，北京 102206；2.国电普迅电力信息技术有限公司，天津 300384）

0 引言

空间负荷预测 SLF（Spatial Load Forecasting）是电网规划的基础[1]。近年来，人们提出了许多空间负荷预测模型[2-9]，其中，用地仿真法是目前精度最高的一种空间负荷预测模型，它通过建立用地仿真模型模拟小区未来的发展情况，最终将负荷总量预测结果分配到各小区。然而在用元胞自动机模拟用地类型变化时，往往假设在整个元胞空间内所有元胞都按相同的转换规则演化，采用统一的转换规则来驱动元胞自动机模型中所有元胞的演化，进而来模拟用地类型的变化，所以这种方式忽略了用地类型变化的空间异质性，从而影响了元胞自动机模型的模拟精度，而负荷预测的准确性直接影响着电网系统投资及运行的合理性。针对该问题，本文研究了按照空间变异系数的大小对元胞空间进行不规则区域划分的方法，分区的大小随着变异系数的不同而变化，这样每一个分区内具有相对一致的元胞转换规则，用元胞自动机模拟演化的结果也将更加准确。考虑到影响负荷预测的许多因素存在于不同的尺度[10]之中，单一的尺度可能会导致影响负荷预测精度的一些因素、甚至是重要因素的缺失。由于不同尺度的区域划分方式会对地理信息表达的正确与否产生影响，很多地理现象和规律只有在特定的尺度下才会出现。因而，本文提出了多尺度区域划分的方法，按照相邻分区相似度对利用变异系数大小划分得到的分区进行聚类融合，相似度阈值不同，则得到不同尺度的区域划分，而每一尺度下各个分区都有各自独立的元胞转换规则，最后将每一尺度得到的结果进行叠加分析，提高了元胞自动机模型的运用有效性和时空模拟精度。

1 相关概念

所谓空间异质性，是指区域化变量在不同空间位置上由于空间数据受到总的条件或规律的制约而存在明显差异的属性。在进行空间负荷预测时，经常需要对用地类型进行预测，然而由于受到周围环境的影响程度不同，不同空间位置转换为不同用地类型的概率就会有很大的区别，因此采用统一的元胞区间划分方法忽略了空间位置的这种差异。

通常采用变异函数来表示两点之间区域化变量值的相关性。当空间点在一维x轴上变化时，区域化变量在 xi和 xi+h 处的值为 Z（xi）和 Z（xi+h），两者之差的方差的一半定义为区域化变量在x轴方向上的变异函数，其中xi是x轴上某一点的取值。变异函数记为[11]：

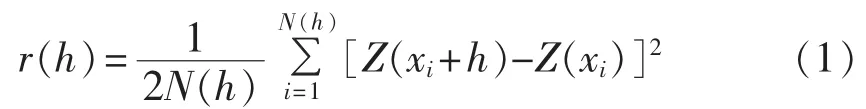
其中，N（h）为间隔距离是h的样点数。

元胞自动机具有模拟复杂系统时空演化过程的能力，它包含4个基本要素：元胞、状态、邻域和转换规则，可以用形式语言表示为[2]：

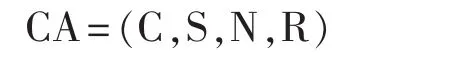
其中，CA为元胞自动机；C为元胞，是研究区域的最小面积单元；S为元胞状态，本文中元胞状态有4种，即居民生活用地、工业用地、商业用地、市政用地，某时刻t元胞状态只可能是有限状态中的一种；N为邻域即元胞的邻居，本文采用比较稳定的Moore型邻域，如图1所示，图中黑色元胞为中心元胞，灰色元胞为其邻居；R为转换规则，转换规则的定义是元胞自动机的核心，传统的转换规则只考虑邻域的影响，本文中的转换规则综合考虑了空间异质性和尺度等因素的影响。

图1 Moore型邻域Fig.1 Moore neighborhood

简单而言，元胞自动机可视为由一个元胞空间和定义于该空间的变换函数所组成。元胞的状态随着时间根据一个局部规则来进行更新变化，即一个元胞在某时刻的状态取决于且仅取决于上一时刻该元胞的状态以及该元胞的所有邻居元胞的状态。元胞空间内的元胞依照这样的局部规则进行同步的状态更新，整个元胞空间则表现为在离散的时间维上的变化，非常容易在计算机中建模与仿真。元胞自动机采用“自下而上”的建模方法，通过元胞之间、元胞与环境之间的交互来进行时空演化，这种不同于以往纯数学建模的新计算范型思想是用局部作用规则控制元胞的行为，最终使系统呈现出宏观上的稳定秩序。

为了下文描述的方便，本文中引入2个新概念，即变异系数与尺度，其详细定义如下。

定义1：在空间变异函数中，假设区域化变量Z（xi）为空间实体对周边环境的影响程度，则称 ω（h）=为 到 的空间变异xixi+h系数，并用它来表示空间变异性的大小，如果该值大则说明空间变异性程度较大，显然ω（h）的取值范围为[0，1]。

定义2：假设研究区域的总面积为D，划分各元胞小区的面积分别为 D1、D2、D3、…、Dn，n 为元胞空间中元胞的总数目，令 rn=（1 /D1，1 /D2，…，1/Dn），则称该区域划分方式为rn尺度区域划分。此时rn是一个数据序列，用来表示一组大小不等、非规则的小区。

2 顾及空间异质性的多尺度空间负荷预测模型

2.1 模型的建模流程

顾及空间异质性的多尺度空间负荷预测模型的建模流程见图2，建模过程具体如下。

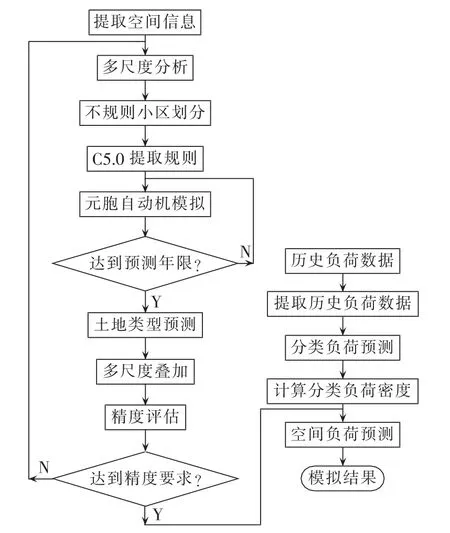
图2 顾及空间异质性的多尺度空间负荷预测模型的建模流程Fig.2 Flowchart of modeling for multi-scale spatial load forecasting considering spatial heterogeneity

首先，用于空间负荷预测的数据在地理信息系统中经过数据预处理、对齐与裁剪等处理后，转换成多尺度分析以及不规则小区划分可以识别和处理的数据[12]；其次，按照空间变异系数的大小对元胞空间进行不规则的区域划分，这样每一分区具有了相对一致的转换规则，并以此不规则区域划分为基础，对不规则分区进一步聚类融合以得到更高尺度下的分区结果，即进行多尺度的区域划分，在多尺度划分的过程中，本文引入了粗糙集理论来对影响分区融合的众多因素进行属性约简，从而减少了数据量使结果更加高效可靠；然后采用C5.0决策树算法，将不同尺度下的每一分区分别构建动态的转换规则，并将分区结果和各分区的转换规则输入到元胞自动机中进行土地类型的变化模拟，将得到的模拟结果与实际区域的土地类型进行对比评估，如果模拟结果与实际类型相比达到了指定的精准度要求，就可以将模型应用于空间负荷预测，否则重新进行多尺度下对每个分区采样从而获取新的转换规则，重复上述过程直到精度满足要求；接着对历史负荷数据进行分类负荷预测，并计算出分类负荷密度，由于现阶段分类负荷预测模型已经比较成熟，模拟得到的结果已具有相当高的精准度，因此本文重点研究对空间异质性的处理，即如何在多尺度下对研究区域进行不规则划分以及模拟结果的多尺度叠加分析；最后，将空间负荷预测的模拟结果送回到地理信息系统中显示[13]。

2.2 基于空间变异系数的不规则区域划分

考虑到空间的异质性特征对区域现象和规律模拟的影响，同一个转换规则不可能适用于整个元胞空间。因此本文中按照空间变异系数的大小，对元胞空间进行不规则的区域划分，使得每一区域具有相对一致的元胞转换规则，从而驱动元胞自动机的时空演化，该步骤也是多尺度分析的核心部分。具体操作过程如下。

a.在研究区域内随机选取重要地点，如重要居民小区、商业网点以及交汇点等，将这些重要地点都标识为未标记。其他所有地点如绿地、湖泊、高山等都作为空间中的一个点，初始时空间中的所有点都未被标记。

b.以重要地点为初始中心出发点，从空间中该中心点向周围各个方向的其他所有点计算未标记点的空间变异系数ω（h），不断增大h的值，如果ω（h）的值大于阈值α，则停止该中心点向该方向的空间变异系数计算，并对该点做标记处理。

c.如对已标记的同一空间点计算得到多个空间变异系数值ω（h），则取其最小值，并归入到相应的初始中心点。

d.以重要地点为中心点，向各个方向找到最近的已标记的空间点，并将这些空间点围成的区域作为一个单独的分区。

e.重复上述所有步骤，直到元胞空间中所有的点都划分到一定的分区中，此时完成单一尺度下的不规则元胞区域的划分。

通常利用空间变异系数对元胞空间进行不规则划分时，初始阈值α置为1。在实验过程中，需要不断调整阈值α，使预测结果更接近实际情况。

2.3 多尺度区域划分

不同的尺度会对地理信息的正确与否产生影响，因为影响负荷预测的许多因素存在于不同的尺度之间，仅考虑单一的尺度可能会忽略一些重要的因素，从而影响负荷预测的准确率，而且很多地理现象和规律只有在特定的尺度下才会出现。因而选择不同的尺度，可能会导致对空间过程及其相互作用规律不同程度的把握，最终将影响到研究成果的科学性和实用性。因此本文提出了多尺度的区域划分方法，该方法的操作过程如下。

a.找到影响元胞分区相似度的因素。影响2个分区相似程度的因素非常多，一般包括交通通达程度、公共设施便利性、教育资源、自然环境质量、住房价格、经济能力、职业、家庭结构（有无小孩）、年龄、受教育程度、居民生活质量、科教水平等。

b.利用粗糙集理论来对众多的影响因素进行属性约简。为了找到影响元胞分区相似度的重要因素，忽略不太重要的影响因素，本文中引入了粗糙集理论来对众多的影响因素进行属性约简，粗糙集约简方法详见文献[13]，最后得到了最重要的4种影响因素，如表1所示。

c.聚类融合得到更大尺度的区域划分。以基于变异系数得到的不规则元胞空间划分区域为基础，将不规则元胞分区按照相似程度阈值β来进行聚类融合，这样分区的数目将进一步缩小，即得到更大尺度下的空间负荷预测结果。

表1 影响分区融合的主要因素及其权重Tab.1 Main affecting factors on partition integration and corresponding weights

d.调整阈值得到多尺度下的区域划分。当相邻2个分区的相似度超过β（首次取β=0.8）时，将2个分区融合为1个分区，最终得到该尺度下的区域划分。依此类推，可以得到β值为0.6、0.4、0.2等多种尺度下的区域划分，直到分区数量为1时停止。如此即可得到多尺度下的不规则分区。不规则区域的划分结果与实际情况相符合，以此为基础提取元胞自动机规则也将更加准确。

2.4 元胞自动机规则提取及多尺度叠加分析

决策树是按照不同的特征，以树型结构来表示决策集合或者分类，最终产生规则并发现规律。C5.0是经典的决策树模型算法之一，可生成多分支的决策树。它的主要作用在于揭示数据中的结构化信息，所建立的树型结构直观、易于理解，而且便于处理非线性数据的描述数据，能提取数据中隐藏的知识规则。因此，C5.0决策树模型可以用于元胞自动机模型转换规则的挖掘。本文中的目标变量即为土地类型分类变量，使用C5.0算法可以生成相应的决策树或者规则集。首先将经过多尺度划分处理后的空间数据及划分得到的不规则分区作为训练样本输入到C5.0决策树模型进行学习，对于对模型值没有显著贡献的样本子集将被剔除或者修剪，通过不断调整模型参数最终建立起土地类型分类规则；然后依据分类规则，实现对其他新输入样本数据的分类；最后将建立好的样本规则以及不规则的分区数据，输入到元胞自动机模型来模拟土地类型的时空演化[14]。本文中采用C5.0决策树算法来对多尺度下不规则的分区分别提取元胞转换规则，有了上述基于空间变异系数的不规则区域的划分，每一分区便具有了相对一致的转换规则，因而元胞自动机规则的提取将变得十分容易而且提高了空间演化模拟的精准度。

在不同尺度下分别对用地类型进行预测，然后将不同尺度下得到的预测结果进行叠加，示例效果如图3所示，其中第1层为r1尺度划分方式，第2层为r4尺度划分方式，第3层为r16尺度划分方式，每个尺度上的观测数据以及不同数据之间的关系反映了土地的利用类型以及不同尺度对土地利用类型转换的影响。目前将不同尺度的数据很好地整合到一起的方法主要有“紧”整合和“松”整合。“紧”整合要求不同尺度的区域范围是一致的，而“松”整合则没有这样的要求，因而适用于任何尺度的数据整合[15]。本文主要借鉴文献[15]“松”整合的思想方法，通过经纬度将不同尺度下的数据叠加来实现预测结果的叠加分析，如果某点转化为某种用地的数量多于其他用地类型，则该点区域用地类型转换为相应用地类型的可能性越大。

图3 多尺度叠加示意图Fig.3 Schematic diagram of multi-scale superposition

最后，根据模拟区域的每一类土地的使用情况，按照式（2）预测出每一类负荷密度：

其中，Ii表示第i种用地类型的负荷预测值，Ai表示第 i种用地类型的总面积，i=1，2，…，m，m 为用地类型总数。对于划分的每个小区，它的预测负荷值Wj等于该预测的小区土地使用面积 Lj（j=1，2，…，n，其中n为划分小区的总数）乘以该小区的预测负荷密度 Pi（i=1，2，…，m），其计算公式为：

3 顾及空间异质性的多尺度空间负荷预测模型的模拟应用

3.1 数据预处理

本文针对某市的实际情况，对其电力负荷在空间上的分布做了详细研究。本实验的基础数据包括该市2005年至2010年负荷历史数据，2005年、2006年和2010年该市中心城区TM遥感影像图、交通图、地图，以及该市分区人口统计数据、土地利用总体规划图、行政界线图、地形图、DMS馈线用电负荷历史统计、营销信息系统用户的报装信息等。通常在能够满足配电网规划的要求下把用地类型简单地分为工业、商业、居民、市政4类，这样就极大降低了工作量和难度。之所以要对用地类型进行划分，是因为不同的用地类型具有不同的负荷密度曲线，会影响分类负荷密度的计算。

3.2 实验处理及结果分析

本文采用顾及空间异质性的多尺度空间负荷预测模型，从研究区域选取重要地点共计366个，其中重要居民小区58个、商业网点236个、交汇点23个，其他重要地点49个。以这些重要地点为初始中心出发点，按照空间变异系数的公式计算各个点的空间变异性大小，将点区域划分归并到变异性最小的中心点，这样每一分区便具有了相对一致的转换规则。接着用C5.0决策树算法分别获取每一不规则分区的元胞转换规则，以此驱动不同分区的元胞进行时空演化。然后根据用粗糙集理论对所选择的众多影响相邻分区的因素进行属性约简，得到4种最重要影响因素及其权重，接着按照不同权重计算得到相邻分区之间的相似度，并按照相似度阈值β将相邻的分区进行融合，初始β=0.8，这样分区的数量将变少，即得到该尺度下的分区划分。不断调整相似度阈值直到分区数目变为1为止，如此便得到了多尺度下的分区划分结果。本研究区域按照相似度阈值β=1、β=0.8、β=0.6、β=0.4、β=0.2、β=0.09 以及 β=0共得到7种不同尺度的区域划分，分别为r214、r176、r131、r87、r45、r8和 r1尺度，其中 r214表示由 214 块不规则分区组成的尺度划分，其他依此类推，图4所示为r8尺度的分区结果。不同尺度下的空间负荷预测结果因为受不同尺度下各影响因素作用的不同而产生差异，本文根据“松”整合的思想，按照经纬度对不同尺度下的分区结果进行分层叠加，如果不同层相同经纬度下的某一点区域转换为某种用地类型的数据量较多，则该点区域转换为相应的用地类型。2010年该市实际土地利用分布情况与本文模拟预测土地分布结果如图5、6所示，可以看出模拟结果与实际土地类型基本一致，因此可以将本文模型进一步应用于空间负荷预测。利用式（2）与式（3）计算即可求得空间负荷预测结果，图7、8分别为2010年该市实际空间负荷分布与本文模型得到的空间负荷预测结果，图中深色点的密集程度表示负荷密度的大小。可以看出，2010年该区域的实际负荷分布主要集中在西北部一带，因为该区域有大规模的工业园区，用电量会较其他区域要大，而其他的一些用电量主要集中在大型的商场、市政办公楼、高层建筑、学校以及写字楼等区域，使用本文提出的模型来预测该区域2010年的负荷分布情况同实际负荷分布情况大体一致。

图4 r8尺度的分区结果Fig.4 Regional divisions of r8scale

图5 2010年该市实际土地利用分布Fig.5 Actual distribution of municipal land use in 2010

图6 本文模拟预测土地利用分布Fig.6 Distribution of land use forecasted by proposed model

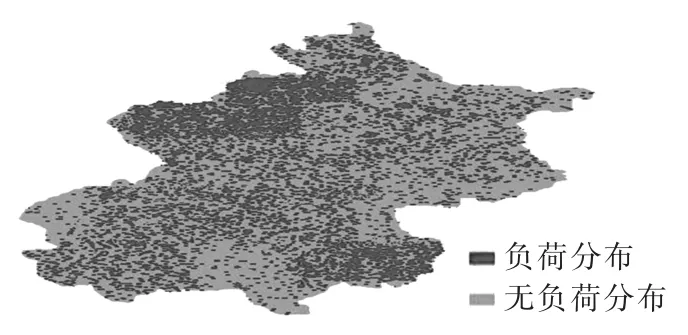
图7 2010年实际空间负荷分布Fig.7 Actual distribution of special load in 2010

图8 2010年顾及空间异质性的负荷分布Fig.8 Load distribution considering spatial heterogeneity in 2010

为了验证顾及空间异质性的多尺度空间负荷预测模型的有效性，本文将该模型得到的预测结果与实际负荷分布结果进行了对比，结果如表2所示。由表2可见，顾及空间异质性的空间负荷预测模型的模拟结果，更接近实际的负荷利用总体结构和形态。

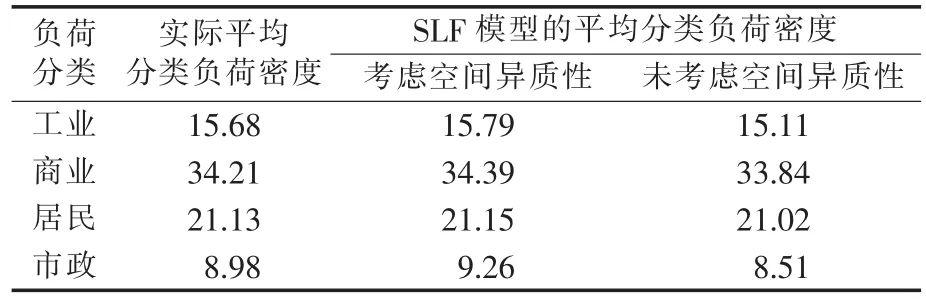
表2 2010年空间负荷预测结果对比Tab.2 Comparison of forecasted spatial load for 2010MW/km2

此外，本文采用元胞自动机模型精度评估最常用的逐点对比法对本文元胞自动机模型精度进行检验，该方法通过逐像元对比元胞自动机模型的模拟结果与实际的分布来衡量元胞自动机模型的模拟精度。本文在程序中分别对实际分布和模拟分布的每一像元是否有负荷分布进行标识并计数，最后通过计数比值即可得到模拟分布的精度值。如图7和图8结果所示，与2010年该市空间负荷实际分布状况对比，采用顾及空间异质性的多尺度空间负荷预测模型的精度达98.86%。因此，顾及空间异质性的多尺度空间负荷预测模型模拟精准度更高，具有很强的实用性。

4 结语

采用统一的元胞转换规则驱动元胞自动机进行时空演化，是在假设所有分区中地理现象服从某单一均质性的前提下进行的，从而忽略了地理现象的空间异质性，因而影响了空间负荷预测的精度。本文针对以上问题，提出了顾及空间异质性的多尺度空间负荷预测模型，该模型按照空间变异系数的大小将元胞空间进行不规则划分，使每一分区具有相对一致的转换规则，同时再对已有的不规则分区按照相邻分区的相似度进行聚类融合，由于影响因素较多，本文中引入了粗糙集理论来对众多因素进行属性约简，根据不同的相似度阈值，得到了多尺度的区域划分。在此基础上，对不规则的分区采用C5.0决策树算法，挖掘每一个子区域的元胞转换规则来驱动元胞自动机模型模拟区域土地类型的变化，最后将每一尺度下得到的模拟结果进行叠加，经过实例验证本文模型可以获得与实际非常接近的模拟效果。