计及车主满意度的电动汽车最优峰谷分时电价模型

高亚静 ，王 辰，吕孟扩 ，梁海峰

（1.华北电力大学 新能源电力系统国家重点实验室，河北 保定 071003；2.中广核工程有限公司，广东 深圳 518124）

0 引言

在能源危机及环境污染的大背景下，电动汽车因零污染、低噪音等优点，获得了愈来愈多的关注。考虑到电动汽车充电行为的随机性，大量电动汽车接入会给电力系统的运行与控制带来显著的不确定性[1-3]，此外电动汽车还可以在用电高峰期将电能放回电力系统中，即 V2G（Vehicle to Grid）[4-6]。 如果没有相应的政策和手段来对其充、放电行为进行引导，那么大规模的电动汽车无序充放电行为将对电力系统的运行与规划产生非常不利的影响[7-9]。由于电动汽车充放电行为是完全从属于车主的私人意愿，常规的调度手段将不再适用于电动汽车，而峰谷分时电价能够通过自身的经济杠杆作用来刺激和鼓励电动汽车改变其充放电行为，使得电网和电动汽车车主双方面均收益[10-12]。

本文从影响电动汽车功率需求的两大因素，即充电开始时刻以及日行驶里程入手，建立了电动汽车的充、放电功率模型，然后基于电动汽车车主满意度以及电网利益的考虑，设计了适用于电动汽车充放电的最优峰谷分时定价方案。

1 电动汽车充电功率建模

1.1 假设条件

本文以利用分布式充电桩进行常规慢速充电的电动汽车作为研究对象，并建立其充电模型。

单台电动汽车充电模型的建立可通过该电动汽车的充电开始时刻以及充电时长得到。开始充电时刻和日行驶里程则取决于用户的出行习惯和行驶特性，最后行驶返回时刻以及日行驶日程在本文中被认为是相互独立的[13]。

参考目前电动汽车的发展状况，本文对使用充电桩充电的私家车做出如下假设：

a.每100 km耗电量固定为15 kW·h；

b.在分时电价未实施的情况下，电动汽车在每日最后一次出行返回后开始充电；

c.本文的充电过程将近似为恒功率特性，因为对于使用充电桩进行常规慢速充电，充电起始和结束阶段相对于整个充电过程而言较短，可以忽略；

d.每次充电都充至满电量；

e.在本文中V2G的放电被认为是一个负的负荷，并且其相关特性与充电相似；

f.最后行驶返回时刻及日行驶日程是相互独立的随机变量；

g.由于本优化模型不影响电动汽车的充电次数，所以不计由于电动汽车电池充电造成的动力电池本身损耗的成本。

1.2 最后一次行程结束时刻和日行驶里程概率模型

用极大似然估计的方法分别将车辆最后行程返回时刻和日行驶里程近似为正态分布和对数正态分布。最后一次行程结束时刻，即开始充电时刻，其概率密度函数可表示为[14]：

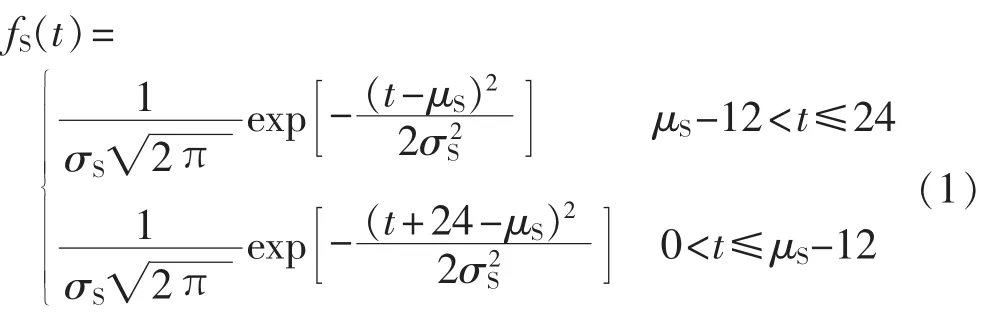
其中，t为开始充电时刻；μS=17.6；σS=3.4。

日行驶里程表示一辆电动汽车单日内行驶里程，其服从对数正态分布，概率密度函数表示为：

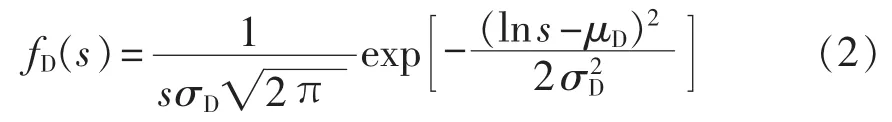
其中，s为电动汽车日行驶里程；μD=3.20；σD=0.88。

为简化分析，设定从i到i+1时刻内开始充电的电动汽车均从i时刻开始充电，表示为：

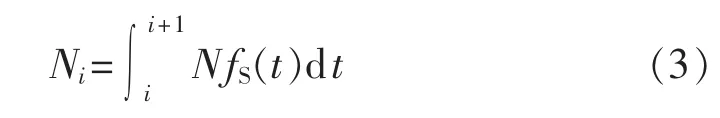
其中，Ni（i=1，2，…，24）为从 i到 i+1 时刻内开始充电的电动汽车数量；N为电动汽车的总数量。

基于电动汽车不同的日行驶里程，本文对其进行了分类：如果一辆汽车日行驶里程处于0～m km的范围内，则认为该辆车日行驶里程为m km，并标记为第1类电动汽车；行驶里程在m～2m km范围内，则认为该辆车日行驶里程为2m km，并标记为第2类电动汽车；同理，不同日行驶里程的汽车将会被分为若干类别。

因此，在i时刻开始充电的行驶里程为第k类的电动汽车数量可表示为：

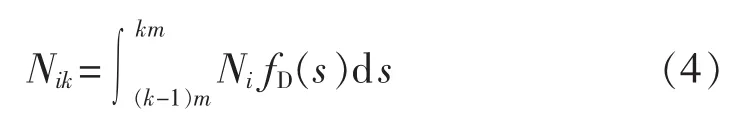
在i时刻开始充电的行驶里程为第k类电动汽车的充电时长可表示为：

其中，Sk为行驶里程为第k类的电动汽车的日行驶里程；W为汽车每行驶100 km所消耗的电能；Pc为充电功率。

2 电动汽车充放电的需求响应模型

本文将电动汽车的行驶状态分为如下2种。

第1种是日常行驶和作为储能装置在负荷高峰时段向电网放电。为便于分析，本文假设第1种状态的时间段为结束当天行程时刻的前12 h。

第2种是结束当天行程后的充电状态。第2种状态为结束当天行程时刻的后12 h，这就意味着电动汽车必须在结束当天行驶时刻之后的12 h内充满电。

在峰谷分时电价方案实施后，根据电动汽车对电价的响应方式不同，将电动汽车分为A、B、C 3类。

a.A类电动汽车：在峰谷分时电价方案实施后，此类电动汽车将改变充电开始时刻，转移充电负荷，以获取相对低廉的电费支出，但此类电动汽车不参与V2G放电。

b.B类电动汽车：在峰谷分时电价方案实施后，不改变充电开始时刻，但参与V2G，在能够获得放电收益的时段向电网送电，并因此相应地延长充电时长。

c.C类电动汽车：在峰谷分时电价方案实施后，既不改变充电开始时刻也不参与V2G，即对电价无任何响应，与峰谷分时电价方案实施前的充电行为并无二致。

在对电动汽车状态以及响应分类的基础上，研究电动汽车用户的电力需求对电价的具体响应是实现电动汽车充、放电建模的关键步骤。一般情况下，当电价升高时充电的需求会相应减少。在V2G模式下，放电电量将会随电价增长而上升。对于电价所引发的电力需求侧响应即所谓的由弹性系数所表示的需求价格弹性如下[15]：

其中，Δd和Δρ分别为需求与价格的变化量；d0和ρ0分别为需求和价格的基准值。

负荷特征不同的用户对电价的敏感度各不相同。目前电力公司将用户基本分为大用户、非工业和普通工业（简称非、普工业）、商业、农业、非居民照明、居民用电六大类。每种类型用户对应一种对电价反应曲线。本文通过文献[16]中得到的居民分时电价综合反应曲线来近似表征电动汽车用户对电费的响应关系：

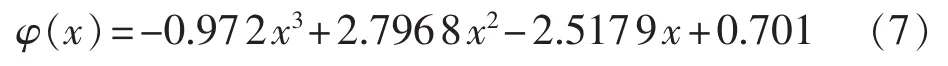
其中，x为电费变化率；φ（x）为车辆数量变化率。

2.1 A类电动汽车的需求响应模型

一辆在i时刻开始充电、行驶里程为第k类的电动汽车，其达到满充所需缴电费表示为：

其中，Qik为一辆第k类汽车在i时刻开始充电直至满充所交的电费；ρn为n时刻的电价。

考虑到充电时长，在i时刻开始充电、行驶里程为第k类的电动汽车能够将充电开始时刻从i转移至使充电费用最小的时刻 j（j∈（i+1，i+2，…，i+12-Tik）），一方面满足结束当天行驶时刻之后的12 h内充满电的设定，另一方面达到负荷转移的目的。因此，对于A类电动汽车，在峰谷分时电价实施后，行驶里程为第k类的电动汽车在j时刻开始充电的数量等于从i时刻转移至j时刻的数量，记作NjkA：

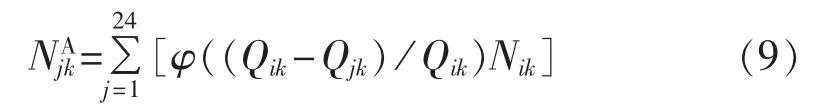
2.2 B类电动汽车的需求响应模型

日行驶里程为第k类的电动汽车的放电能力是满状态下电池电量与日行驶所消耗的电量之间的差额，日行驶里程越大的汽车用于行驶的电能消耗得越多，所具备的放电能力就越小，反之则放电能力越大。在恒定的放电功率情况下，其放电能力可用放电时长来表示：

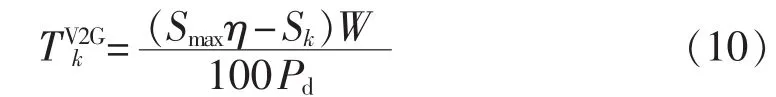
其中，Smax为最大日行驶里程，用以表征满状态下电池电量；η为放电的容量约束，表示实际中电池放电不能全放完；Pd为放电功率。

设峰时刻为 t1、t2、…、tf，考虑到峰谷时刻的划分安排，日行驶里程为第 k 类，在 i（i∈（t1，t2，…，tf，…，tf+12））时刻下开始充电的电动汽车均可以不同程度地参与V2G向电网放电。其最终放电时长与i和k这2个变量有关，经过相关计算比较，可得到使电动汽车用户受益最大化的实际最终放电时长的值，记作TV2Gik。

由于参与V2G的电动汽车将多余的电能向电网放电，其充电时间将会相应地延长，记作TikB：

在电价的刺激下，在i时刻的第k类电动汽车参与V2G项目时，其所应缴纳的电费等于充电费用减去放电收益，可由下式得到：

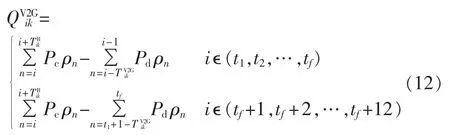
因为B类电动汽车在峰谷电价实施后比之前多了放电行为，这将会导致对电池价值的额外损耗，故将电池的放电损耗纳入成本分析。

选择参与V2G放电的汽车数量因峰谷电价差的拉大而增加。参与V2G的i时刻、行驶里程为第k类的电动汽车数量记作NikB，表示如下：

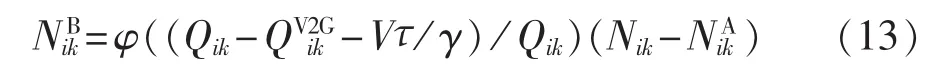
其中，V为动力电池成组后的单位成本；τ为电动汽车电池的装载容量；γ为电池充放循环次数；Qik-QV2Gik为参与V2G的单台电动汽车在选择不参与V2G与参与V2G时所缴电费差额，其值必须大于因V2G所导致的电池价值的损耗，否则车主会因为参与V2G得不偿失而拒绝向电网送电。

2.3 C类电动汽车的需求响应模型

对于对电价无响应的C类电动汽车而言，在i时刻第k类汽车数量可表示为：

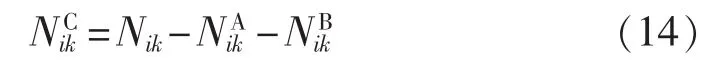
根据以上公式，在实施峰谷分时电价和V2G后，每个时刻的平均负荷可由式（15）计算得出：

其中，ρf、ρp、ρg分别为峰、平、谷时段电价。

3 最优峰谷分时电价求解模型

本文所建立的峰谷电价模型旨在统筹考虑电网及车主双方的利益，一方面利用削峰填谷来提高电网负荷率，另一方面人性化地提高车主对峰谷分时电价制定的满意程度。

3.1 用户满意度

本文中的用户满意度是指从电动汽车车主用电方式和电费支出2个方面进行考虑。

a.用电方式的满意度是衡量用户用电方式变化的指标，在未实行峰谷电价之前，车主在结束当日行程后立即进行充电，此时用户的用电方式满意度最大。实行峰谷电价后，车主通过改变开始充电时刻以及是否参与V2G来减少电费，从而形成新的负荷曲线，这意味着车主用自己的一部分用电自由来换取经济利益，因此用电方式的满意度可表示为：

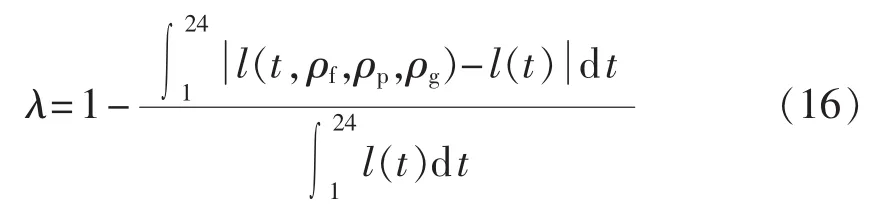
其中，l（t，ρf，ρp，ρg）为电动汽车在实施峰谷电价后在 t时刻的负荷；l（t）为实施峰谷电价前在t时刻的负荷。

b.电费支出满意度是衡量用户电费支出的变化量的指标。在本文中，C类车主的充电行为不因峰谷电价而改变，这将导致他们所缴的电费会有明显增加，因此不能仅仅考虑电网公司和部分车主的利益而过分损害这一部分车主的利益，制定电价方案时应当考虑这部分车主的电费不会因峰谷拉开比扩大而过分增加，电费支出满意度可表示为：

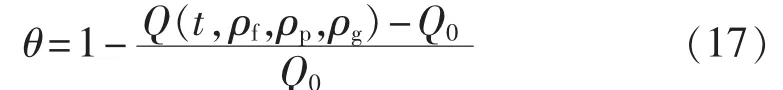
其中，Q（t，ρf，ρp，ρg）为该部分电动汽车实施峰谷电价后所缴电费；Q0为实施峰谷电价前所缴电费。

3.2 目标函数

本文的优化目标为峰负荷最小、峰谷差最小、电动汽车购电费用R2最小、全体电动汽车用户用电方式满意度λ最大以及C类电动汽车用户电费支出满意度θ最大这5个目标函数：

其中，lt为电动汽车在实施峰谷电价后在t时刻的负荷；Lt为一组某地区典型日负荷数据。

约束条件包括确保供电公司获利、确保车主收益以及对电价范围的约束，表示如下：

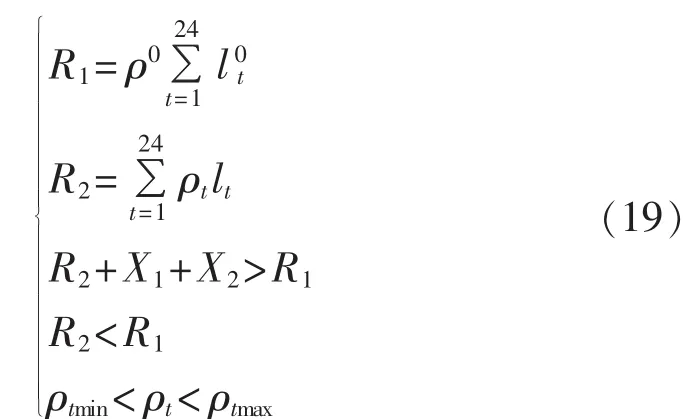
其中，ρ0为峰谷分时电价实施前的电价；l0t为峰谷分时电价实施前在t时刻的电动汽车用电量；ρt为峰谷分时电价实施后在t时刻的电价；X1为供电侧缓建电网的收益；X2为政府对供电公司的补贴；R1为实施分时电价前全体电动汽车的电费；R2为实施分时电价后全体电动汽车的电费；ρtmax、ρtmin为监管部门规定的电价的上、下限。

本文利用粒子群算法[12]对多目标分时电价优化问题进行求解，得到一组Pareto最优非劣解，并根据模糊集理论来确定最优折中解，每个Pareto解中各目标函数对应的满意度ui可用偏小型半梯形和偏大型半梯形模糊隶属度函数来表示，其中偏小型半梯形模糊隶属度函数定义如下：

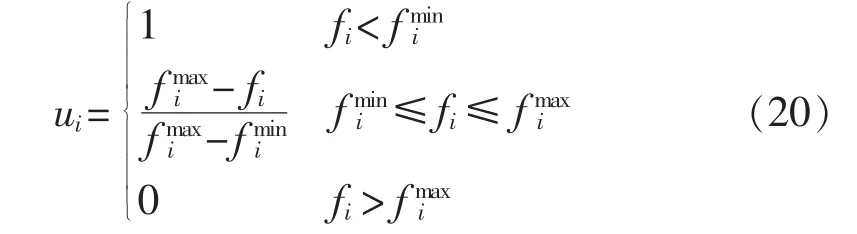
其中，fmaxi为第i个目标函数的最大值；fmini为第i个目标函数的最小值。再采用下式求得Pareto解集中各个解的标准化满意度：

最后通过比较，选取出具有最大μ值的Pareto最优解作为最优折中解。

4 算例

以一组某地区典型日负荷数据为基础负荷，在没有分时电价实施的情况下，叠加上电动汽车充电负荷，形成了电动汽车接入电网随机充电后的负荷曲线。在这条负荷曲线的基础上，利用K均值聚类可以划分出峰谷平时段。再根据电动汽车充放电需求响应模型，可以得到实施峰谷分时电价以及V2G情况下的负荷曲线。将所得到的负荷曲线代入最优峰谷电价优化模型，可得到基于电动汽车车主满意度的最优峰谷电价方案。

电动汽车充放电相关参数设置如下：W=15kW·h，Pc=5 kW，Pd=5 kW，N=300 000，Smax=300 km，ρ0=0.6213元/（kW·h），V=1000元/（kW·h），τ=45kW·h，γ=4500，η=0.8。

图1中电动汽车的充电功率曲线与典型日负荷数据相叠加得到包含电动汽车充电功率的负荷曲线，图中横坐标6是表示时段06:00—07:00，其他依此类推。随着电动汽车的接入，日最大负荷从1271.5 MW增加到1494.8 MW，增长了14.94%，峰谷差从469MW增加到683.5MW，增长了45.74%。在电价为0.6213元/（kW·h）的情况下总电费为1224500元。

图1 未实行峰谷电价的电动汽车负荷Fig.1 EV loads before implementation of TOU price

根据图1可做出峰谷时段划分，采用基于K均值聚类算法的峰谷时段划分方法可对峰谷时段进行有效划分，本文中包含电动汽车充电功率的负荷曲线的峰谷时段划分如下：谷时段为时段 1—8、23、24，平时段为时段9—16，峰时段为时段17—22。

最优的峰谷平时段电价方案可以通过对目标函数求解得出，即 ρg=0.2058 元 /（kW·h），ρp=0.4413元 /（kW·h），ρf=1.0566 元 /（kW·h）。

在峰谷分时电价实施后，3类电动汽车的负荷曲线由图2所示。最优峰谷分时电价执行后的负荷曲线见图3，由图3可知，日最大负荷从1494.8MW减到1335.3MW，峰谷差从683.5MW减到424.2 MW。电动汽车用户所缴电费为872 740元，C类电动汽车用户的电费支出满意度61.9%，总体电动汽车用户的用电满意度92.7%。可见在分时电价以及V2G实施后，在保持电动汽车车主满意度的同时，负荷曲线得到了很大的改善。

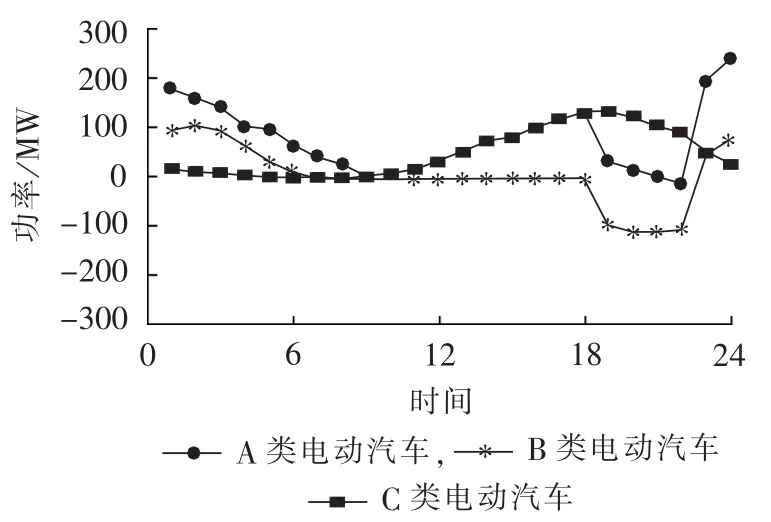
图2 A、B、C 3类电动汽车的负荷曲线Fig.2 Load curves of EV-type A，B and C

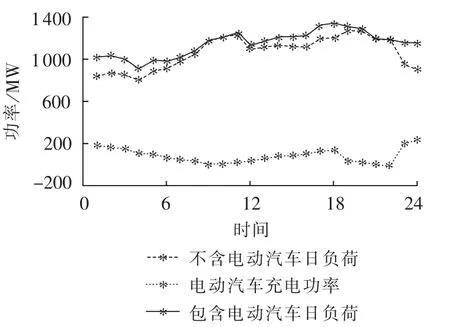
图3 执行V2G的负荷曲线Fig.3 Load curves after implementation of V2G

表1为分时电价及V2G实施前后各项指标的对比。由表1可知，在没有实施分时电价的情况下，电动汽车的无序充电加重了电网负担；而在实施了分时电价后，电网的峰负荷、峰谷差以及电动汽车的电费得到了大幅的降低。

表1 分时电价以及V2G实施前后各项指标的对比Tab.1 Comparison of indicators between before and after implementation of TOU and V2G

5 结论

本文建立了电动汽车对分时电价的需求响应模型，综合考虑电网及车主满意度双方面的利益，在Pareto优化理论基础上，采用粒子群算法对适用于电动汽车充放电的最优峰谷电价方案进行了求解。算例验证表明，在实施峰谷分时电价的前提下，通过V2G车主能够利用闲置的电动汽车在峰时段放电从而获取收益，对于电网，由于V2G能改善负荷曲线，在一定程度上减少了对峰荷机组以及线路的投资。