双馈风电场柔性高压直流接入下的网侧变换器改进Backstepping控制策略

廖 勇，王国栋

（重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044）

0 引言

随着我国风电场开发规模日益扩大，大规模风电场的稳定接入成为电力系统面临的一个重要问题。风电场采用柔性高压直流输电VSC-HVDC（Voltage Source Converter-High Voltage Direct Current）的接入方式[1-2]，相较于传统高压直流晶闸管的在线换流 LCC-HVDC（Line Commutate Converter-High Voltage Direct Current）[3]的接入方式更适合大规模风电场远距离大功率的运行传输[4]，这使得VSCHVDC方式成为当前关注的热点，世界各国都做了相应的工程探索[5]，而我国的上海南汇风电场VSCHVDC接入是国内首条VSC-HVDC示范工程，同时大连跨海VSC-HVDC输电重大科技示范工程也处于论证实施过程。

风电场VSC-HVDC接入结构是一个多变量的耦合非线性系统，VSC-HVDC的控制性能直接影响到风电场运行状况和电力系统的潮流分配。对于该接入结构下的控制设计，通常控制风电场侧的电压源换流器WFVSC（Wind Farm side VSC）为风电场提供一个恒定的交流电压，使其作为一个松弛节点（slack point）[6]，收集风电场送出的风电功率；至于电网侧的电压换流器GSVSC（Grid Side VSC），其首要目标是控制一个稳定的直流链电压[7]，而无功控制部分可以根据实际情况来设定。由于GSVSC在整体系统中起到两方面的作用：一方面，对于VSCHVDC接入结构而言，其直流电压的控制效果直接影响WFVSC对风电场公共耦合点PCC（Point of Common Coupling）的电压控制效果进而影响整体结构的运行效果；另一方面，对电力系统而言，它是风电进入电力系统的直接接入点，其控制运行效果将直接影响到电力系统风电接点处的电能质量，对于整个电力系统的稳定运行具有不可忽视的影响。因此，本文着力研究和改进GSVSC的控制策略，以期能够从VSC-HVDC接入结构和电力系统可靠运行2个方面来做进一步的改善。

对于GSVSC的控制策略，通常是双闭环PI调节的矢量控制，该控制结构虽然简单，但是容易受系统参数变动[8]和外界干扰影响导致控制效果变差，而且目前大多数VSC-HVDC工程的PI调节器参数多采用试凑法或经验法来选取，在系统调试过程中要求较高的技巧和经验，且得到的调节器不一定能使系统性能达到最优状态[9]。为了提高控制器应对系统参数变化和外界干扰的能力，文献[8-11]分别从神经网络滑模控制、粒子群、输入输出反馈线性化以及LMI结构设计的控制角度来做了相应的改进设计，这些控制策略在一定程度上改善了控制性能，但是有关系统直流侧参数和电网电压的波动影响却尚未考虑。近年来，Backstepping控制设计技术已经获得了极大关注[12-16]，其中文献[14]针对 VSC-HVDC提出了一种自适应的Backstepping控制策略，但未考虑直流电容参数变动、电网电压波动以及其他不可预测的外部扰动，而这些实际运行中可能发生的情况则会导致控制器运行状态的变化，进而影响到整体系统的稳定运行。

本文以双馈感应发电机DFIG（Doubly-Fed Induction Generator）风电场VSC-HVDC接入结构为例，针对GSVSC设计了改进Backstepping控制策略，该策略是依据充分考虑交直流侧系统参数变化、电网电压波动和外界不确定干扰的GSVSC修正动态方程而设计改进，并将sign函数和有界的集总不确定量引入控制力的迭代设计中。相应的Lyapunov函数稳定性证明和4种不同干扰情况对比仿真分析，验证了所提控制策略的有效性。

1 DFIG风电场VSC-HVDC接入电网的数学模型

图1为双馈风电场通过VSC-HVDC接入电网的结构，该结构包括双馈风电场、风电场滤波器、WFVSC、直流母线、GSVSC、电网侧滤波器以及风电场侧和电网侧的升/降压变压器等部分。

1.1 双馈风力发电机侧模型

假设双馈风力发电机连接无穷大系统，其电压电流正方向规定按电动机惯例，定子电压相量与d轴重合，即ugq=0。依此定向方式，DFIG在dq同步坐标系下的暂态电压和磁链方程可以整理为（q轴超前 d 轴）[7，17]：

其中，uw、ur分别为定、转子电压空间矢量；ψw、ψr分别为定、转子磁链空间矢量；ig、ir分别为定、转子电流空间矢量；Rs、Rr分别为定、转子电阻；ωw为风电场电压电角频率；ωr为转子电角频率；Ls、Lr分别为定、转子全自感；Lm为定、转子互感；Lsσ、Lrσ分别为定、转子漏感。

1.2 WFVSC模型

WFVSC运行控制中作为一个松弛节点，控制风电场PCC电压的幅值和相位，当风电场接入后，WFVSC自动吸收风电场送过来的功率[20]。WFVSC在dq同步坐标系下的暂态数学模型为：

其中，uwd、uwq分别为风电场母线电压的d、q轴分量；iwd、iwq分别为WFVSC交流侧输入电流的 d、q轴分量；u′wd、u′wq分别为 WFVSC 交流侧基波电压的 d、q 轴分量；Rw、Lw分别为考虑变压器Ts和平波电抗的等效电阻和电抗；ωw为同步旋转坐标系的角频率，也是风电场电网的角频率。

1.3 GSVSC 模型[18]

GSVSC不仅起到控制直流链电压来保障整个VSC-HVDC接入结构的稳定运行的作用；而且作为风电进入电力系统的直接接入点，改善风电进入电网的电能质量。GSVSC在dq同步旋转坐标系下的暂态数学模型为：

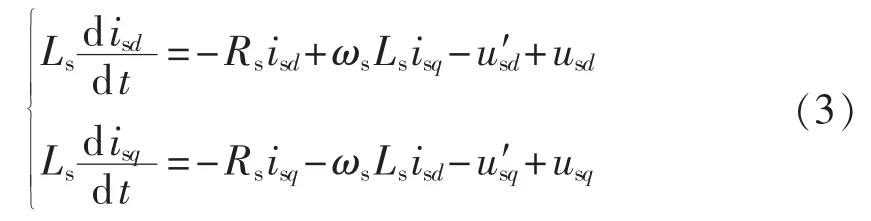
其中，usd、usq分别为电网电压的 d、q 轴分量；isd、isq分别为 GSVSC 交流侧输入电流的 d、q 轴分量；u′sd、u′sq分别为GSVSC交流侧基波电压的d、q轴分量；Rs、Ls分别为考虑变压器Ts和平波电抗的等效电阻和电抗；ωs为同步旋转坐标系的角频率，即电网的角频率。

根据功率平衡的关系，GSVSC侧直流链动态方程为：

其中，Udc2、Idc2分别为GSVSC直流链电压和电流；C2为GSVSC直流链的等效电容。

根据数学模型可以得到其相应GSVSC的等效电路如图2所示。

2 考虑各种干扰的GSVSC修正动态方程

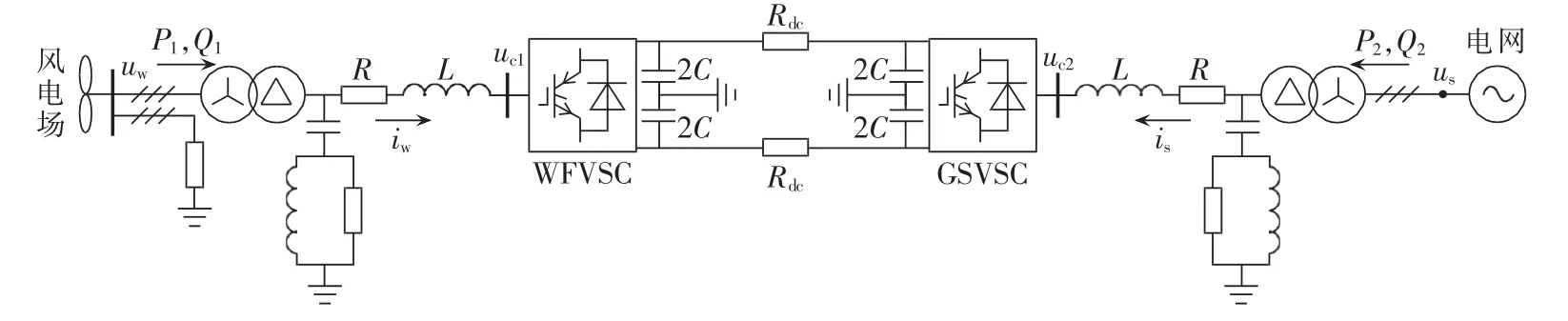
图1 DFIG风电场VSC-HVDC接入电网示意图Fig.1 Schematic diagram of grid-connected DFIG wind farm with VSC-HVDC

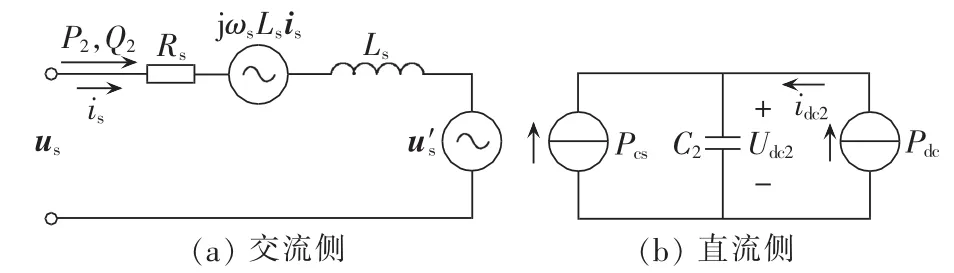
图2 GSVSC交直流侧等效电路图Fig.2 AC-and DC-side equivalent circuits of GSVSC

实际系统的线路额定阻抗是依据系统短路容量来计算的，而在系统运行过程中，GSVSC交流侧输电线路阻抗参数、升压变压器阻抗参数、平波电抗参数以及直流侧的电容参数会受温度、磁芯饱和、输电电缆老化和风能间歇性等因素影响而变化[8]，此外电力系统的电压波动和外界不确定扰动同样也会直接影响GSVSC的控制性能。因此为了充分考虑这些干扰因素，需要对GSVSC的动态方程做进一步的修正。

首先将GSVSC的动态方程式（3）重新整理为：

引入系统参数的变化和其他外部干扰因素，得到新的动态方程为：

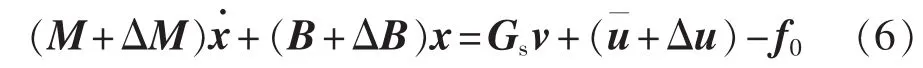
其中，f0为其他外部扰动量，Δu=[ΔusdΔusq]T为电网电压幅值的变化量，为系统参数的变化量。

同样，为考虑电容参数变化对GSVSC控制器设计的影响，对于GSVSC的直流侧动态方程式（4）作同样的整理，得到新的直流侧动态方程：

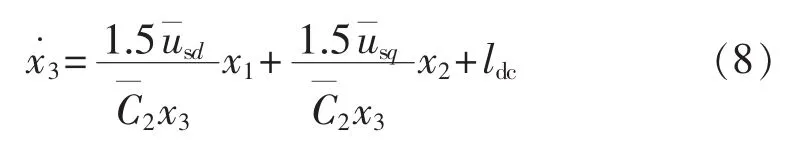
3 GSVSC的改进Backstepping控制策略

由于DFIG风电场VSC-HVDC接入方式具有其独特性，这使得GSVSC的控制目标设计上会与传统链接2个独立系统的VSC-HVDC的控制目标不同。通常一个VSC可以独立解耦地控制其有功和无功的输出，本文从提高DFIG风电场VSC-HVDC接入结构的强健性和最大利用变换器工作能力的角度出发，选取的控制目标分别为稳定直流电压Udc2和变换器单位功率因数运行。

为了实现GSVSC的有功、无功的控制解耦，选取电网电压定向的dq同步坐标轴系，相应的电网电压d、q轴分量为：

定义直流电压控制误差：edc=x3ref-x3，其中x3ref为直流电压的给定参考值，设计第1个的Lyapunov函数为 V1=e2dc/2，结合式（8）和（9）得到 V1微分表达式：

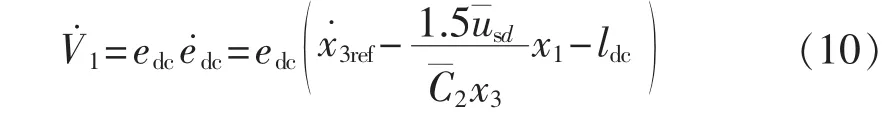
选取x为虚拟控制力，定义它的控制偏差为es=[esdesq]T=α-x，其中 α=[x1refx2ref]T，x1ref和 x2ref分别为各自的控制给定。如果设计x1ref为：

其中，k0是正常数；sgn（·）是 sign 函数。

用所设计的x1ref重新表达式（10）并整理为：

由于本文选取GSVSC单位功率因数运行来充分利用变换器性能，相应设计x2ref=0。

这样，结合式（7）可以得到虚拟控制力的控制偏差es的微分表达式为：

设计第2个Lyapunov函数为V2=V1+esTMes/2，结合式（12）和（13）可以得到：

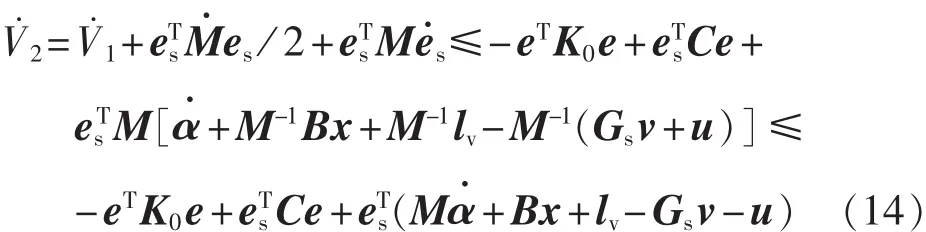
根据式（14），依据Backstepping控制规则设计最终的控制力为：

其中，K1是给定的正常数对角正矩阵。

为了说明所提控制策略的系统稳定性，依据Lyapunov稳定性判别方法，将最终设计的控制力v代入式（14）得到：

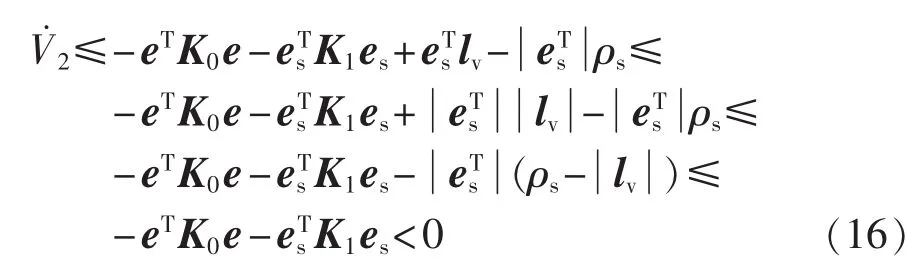
由式（16）的证明可以看出V2是一个负函数，可以推断e和es渐近地趋于0。根据Lyapunov稳定理论，如果GSVSC的交直流侧集总不确定量可以分别满足，那么就可以保障所设计控制策略的稳定性。从整体的控制设计过程来看，改进的Backstepping控制策略是通过引入sign函数和定义有界的集总不确定量，使得设计在控制力中的 ρdcsgn（edc）和 ρssgn（es）分量能够有效应对 GSVSC交直流侧系统参数的变动、外界电网电压波动以及其他不确定扰动的影响。图3给出了具体的GSVSC的控制设计框图。

图3 GSVSC采用改进Backstepping控制策略的控制框图Fig.3 Block diagram of improved Backstepping control strategy for GSVSC

4 GSVSC的Backstepping改进控制策略仿真验证

为了验证本文所提出的风电场电压控制模型的正确性和有效性，以图1所示的DFIG风电场 VSCHVDC接入系统方式为例，采用MATLAB/Simulink仿真验证本文所提的控制策略。仿真中的DFIG风电场总容量为200 MW，采用的DFIG单机容量为2 MW[19]。由于风电场风机数量众多，不便于每一台都有具体仿真模型实现，为了减少仿真负担，本文采用文献[7，20]的单机等效仿真方式来近似模拟整个风电场功率的输出，具体的DFIG等效单机的参数见文献[19]。VSC-HVDC采用三电平中性点箝位的变换器，它比两电平变换器的功率损耗更小[21]。VSC-HVDC的设计容量为200 MW，直流母线电压为±150 kV，直流输电线路长100 km，直流链两端的电容设计为35 μF，对应的时间常数ζ为8 ms，满足小纹波近似和快速响应系统功率变化的要求[22]。VSC开关频率取27×50 Hz，这样产生的谐波频率主要在2.7 kHz及其倍数上，对应的两端滤波器滤除这些高频谐波。风电场通过690 V/35 kV、35 kV/110 kV的两级变压器T1-1、T1-2连接到VSC-HVDC的WFVSC，而GSVSC通过110 kV/230 kV的一级变压器T2连接到受端系统。

对于DFIG的控制策略，本文采用传统的矢量控制，采用定子电压定向[17]的方式，通过解耦控制转子电流的有功和无功分量来实现定子侧输出有功和无功的控制。对于WFVSC的控制设计，本文选取传统的幅相控制[6]方式来为风电场提供一个稳定的交流电压，而风电场的频率由外界直接给定。

4.1 干扰模式设计

为了验证所提改进Backstepping控制策略在改善DFIG风电场VSC-HVDC接入系统下的改进效果，本文从电压波动干扰、交流传输线路参数波动干扰、直流线路电容参数变动干扰以及电网电压外界谐波干扰这几种不确定的扰动因素出发，相应地设计了如下3种干扰仿真对比。

a.干扰模式1：电网电压在1s时跌落20%，并在3 s时恢复。

b.干扰模式2：在干扰模式1的基础上，交流线路阻抗参数及直流电容参数都增加20%。

c.干扰模式3：风电场的风速在1 s时由11 m/s降为 8 m/s，并在 4 s时上升到 12 m/s；此外，电网电压在5 s时出现0.2 p.u.幅值的3次谐波干扰。

4.2 干扰模式1下的对比仿真及分析讨论

图4和图5分别为GSVSC采用传统双闭环PI控制策略和采用本文提出的改进Backstepping控制策略在电网电压出现突变情况下的对比仿真结果（图中纵轴变量均为标幺值）。从仿真过程可见，在风电场风速一定（vwind=11 m/s）的情况下，电网电压在出现一定程度的跌落和恢复过程的时候，传统PI控制方式（图4）下的直流母线电压、GSVSC的有功和无功出现明显的过渡过程，这是因为在系统工作状态变化的情况下，系统运行工作点发生变动，这时的PI参数不再是最优的控制参数整定。此外，图4（f）给出了电网侧a相电压、电流的相位情况（后2个图是第1个图的局部放大图，下同），在电网电压变动的1 s和3 s，电压、电流的相位会出现偏差，这也验证了GSVSC的无功（图4（d））在这2个时间点的变动。而本文提出的改进Backstepping控制策略能够很好地应对电网电压变动的干扰，从图5（b）—（d）可以看出，所提控制策略在直流母线电压控制、GSVSC的有功和无功控制方面都有很好的表现，图5（f）给出的电网侧a相电压、电流的相位情况也说明了所提控制策略对于改善电网侧电能质量的贡献。

图4 干扰模式1下的PI控制仿真结果Fig.4 Simulative results of PI control for disturbance mode 1

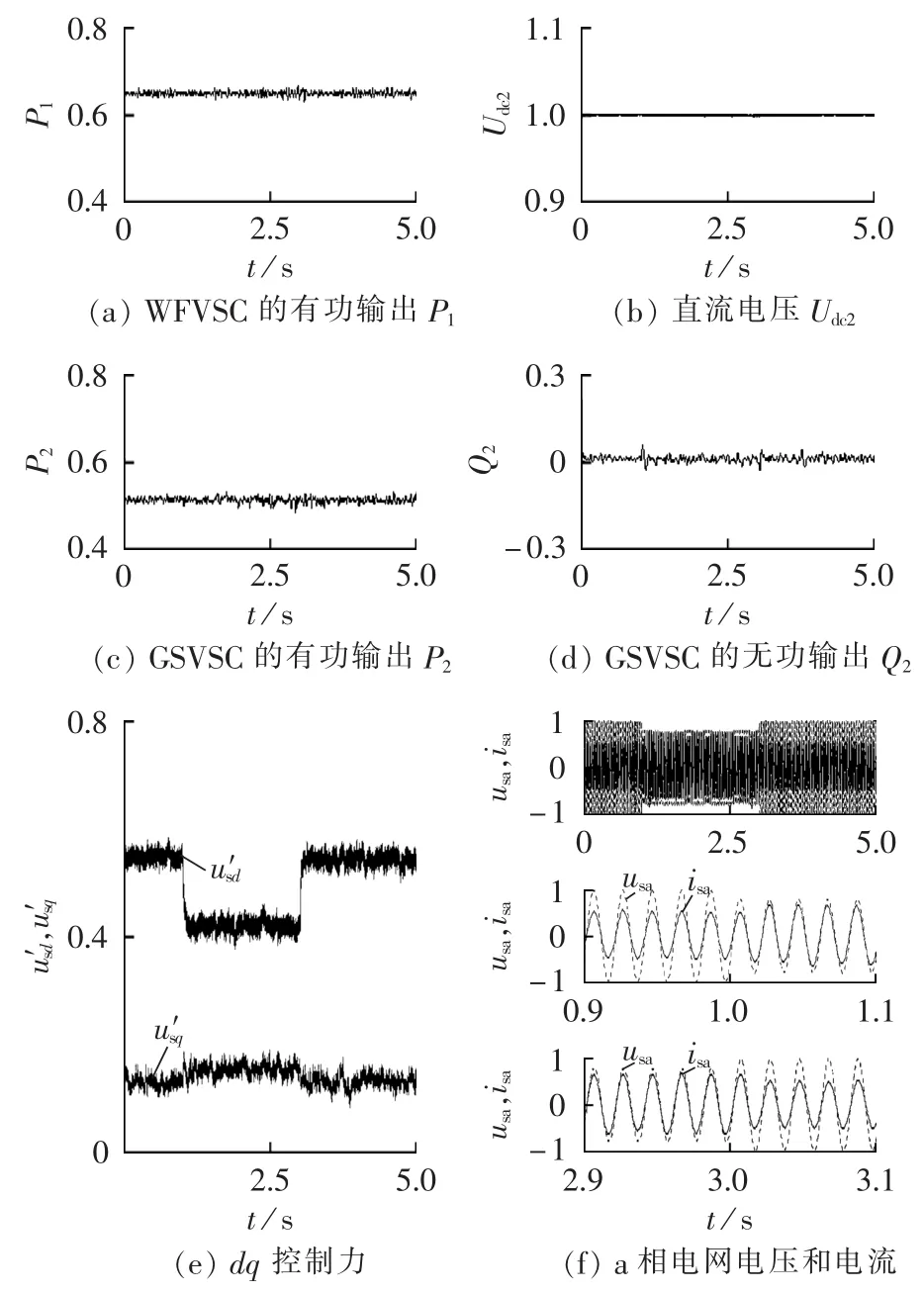
图5 干扰模式1下的Backstepping控制仿真结果Fig.5 Simulative results of Backstepping control for disturbance mode 1

4.3 干扰模式2下的对比仿真及分析讨论

图6 干扰模式2下的PI控制仿真结果Fig.6 Simulative results of PI control for disturbance mode 2

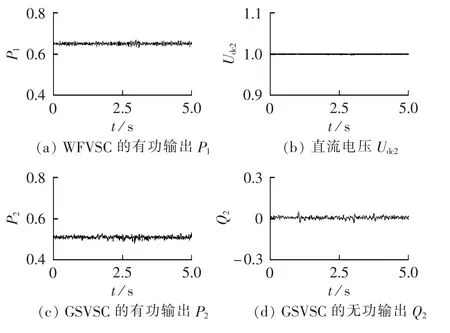
图6和图7分别为GSVSC采用传统双闭环PI控制策略和本文提出的改进Backstepping控制策略在系统交、直流参数出现变动下的对比仿真结果。从仿真过程来看，在风电场风速一定（vwind=11 m/s）的情况下，如果系统交流阻抗参数和直流电容参数出现变动后，对比图6和图4可见，在稳态运行下，系统参数的变动会引起直流母线电压、GSVSC的有功和无功出现一定幅度的抖动，而同样在电网电压变动过程中，系统控制的过渡过程非常明显，这些都说明PI控制策略容易受参数及系统工作状态而不能达到最优的控制效果。而从图7的仿真结果来看，本文所提出的改进Backstepping控制策略能够很好地应对系统参数的变动，保障直流母线电压控制、GSVSC的有功和无功控制的平稳控制效果，改善电力系统风电接入点的电能质量。

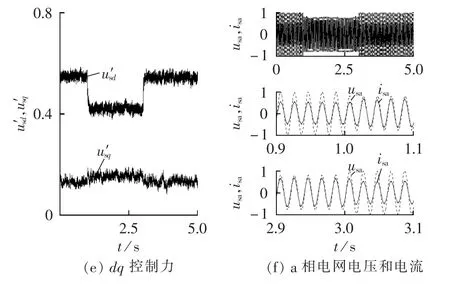
图7 干扰模式2下的Backstepping控制仿真结果Fig.7 Simulative results of Backstepping control for disturbance mode 2

4.4 干扰模式3下的对比仿真及分析讨论

图8和图9分别为GSVSC采用传统双闭环PI控制策略和采用本文提出的改进Backstepping控制策略在风电场风速变动以及电网出现谐波干扰情况下的对比仿真结果。从图8（b）—（d）可以看出在风电场风速变动以及电网出现谐波干扰的情况下，传统PI控制会出现不同程度的过渡过程，从而使得直流母线电压、GSVSC的有功和无功控制效果变差；从图8（a）可以看到WFVSC输入到直流系统的有功由于直流母线电压控制的波动而出现有功的波动，这说明GSVSC的控制性能也间接影响到WFVSC的控制性能。而从图9（b）—（d）可以看出，本文所提出的改进Backstepping控制策略依旧能够很好地应对风电场风速的变动以及外界电网电压的不确定干扰影响，直流母线电压、GSVSC的有功和无功依旧可以达到令人满意的控制效果。此外，从图9（a）也可以看到，WFVSC输入到直流系统的有功相较于图8（a）更加平滑和稳定，这也是GSVSC控制效果改善的印证。

图8 干扰模式3下的PI控制仿真结果Fig.8 Simulative results of PI control for disturbance mode 3

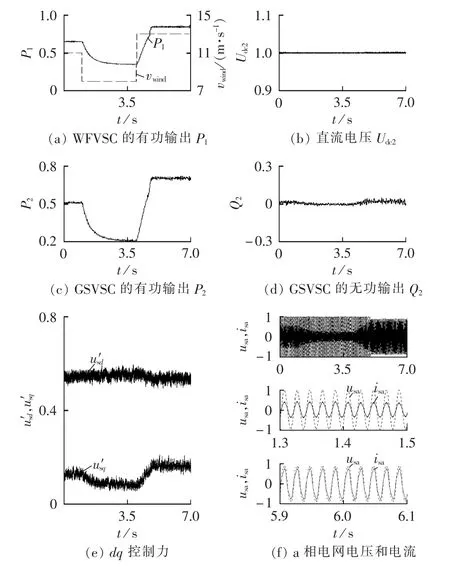
图9 干扰模式3下的Backstepping控制仿真结果Fig.9 Simulative results of Backstepping control for disturbance mode 3

5 结论

本文从DFIG风电场VSC-HVDC接入系统的结构出发，在充分考虑了系统参数变动以及外界不确定干扰因素的影响的基础上，提出了改进的GSVSC的动态修正模型并依此设计了改进Backstepping控制策略，通过一系列的仿真对比分析充分表明：所提控制策略能够得到更加稳定可控的直流电压，系统两端的功率流动也更加平滑稳定，整个系统应对系统参数和外界扰动的运行控制能力更强。这说明改进控制后的DFIG风电场VSC-HVDC接入结构更具强健性和稳定性。此外，电网侧电压电流的控制效果也表明所提控制策略能够改善电力系统风电接入点的电能质量，提高整个电力系统的风电接入能力。