考虑分时电价的电动汽车充电负荷计算

张振夫，黄小庆，曹一家，肖 波，杨 夯

（湖南大学 电气与信息工程学院，湖南 长沙 410082）

0 引言

为了解决目前人类社会面临的严重环境和资源问题，国家正大力推动电动汽车的商业化运营[1]，预计到2020年我国电动汽车保有量将达到500万台[2]。电动汽车大规模入网将对电网造成较大影响，如影响电网网损及电压水平[3-4]、增大负荷峰谷差[5-7]、减少设备寿命[8]、有利于分布式能源优化运行[9-11]等。

分时电价能够引导电动汽车有序充电，降低电动汽车充电对电网的不利影响[12]，而准确计算考虑分时电价的充电负荷分布是制定合理分时电价制度的基础。目前，电动汽车充电负荷计算方法可分为2类：一类针对每辆电动汽车，采用蒙特卡洛模拟方法，反复抽取代表用户用车习惯的随机数，计算电动汽车充电负荷[13-15]，但该方法计算效率较低；另一类则针对一天中的各时间段，根据用车习惯等的概率分布，计算各时段充电负荷的期望值[12，16]，但只能求出近似的数值解，且求解过程较复杂。文献[17]将充电过程离散化计算各时段充电负荷的大小，但是人为指定了开始充电时间，没有考虑车辆实际到家时间的概率分布。

基于上述文献，本文针对一天各时间段内充电负荷的分布情况，将充电过程离散化为多个阶段，考虑驾车习惯的概率分布，提出了一种考虑分时电价的电动汽车充电负荷计算方法，与蒙特卡洛模拟方法相比，该方法具有更高的计算效率，减少了计算时间。

1 充电负荷计算基本假设

考虑到电动汽车的实际发展状况，为了方便计算电动汽车充电负荷，本文做出如下假设：

a.只考虑供私人使用的电动汽车，且电动汽车每天只在家中充1次电；

b.电动汽车每次充电必须将电池充满；

c.开始充电时间与起始荷电状态是相互独立的随机变量；

d.考虑分时电价时，全天分为峰时段与谷时段；

e.分时电价的峰时段电价较高，谷时段电价较低，考虑分时电价后，电动汽车将尽量在充电费用较低的时段里充电；

f.本文考虑10:00至次日10:00间充电负荷的分布情况。

2 考虑分时电价充电负荷计算模型及计算过程

2.1 充电负荷影响因素

本文主要考虑电池充电特性、行程结束时间及每日行驶里程等影响因素计算充电负荷的分布。

2.1.1 电池充电特性

目前电动汽车大多采用锂离子电池作为动力，本文考虑Nissan Altra所搭载的锂离子电池，其容量为 29.07 kW·h，充电功率 P 曲线如图 1所示[18]。

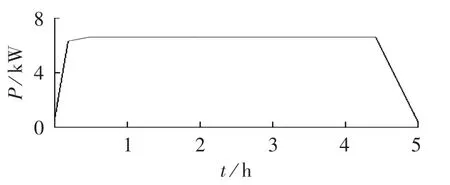
图1 电池充电曲线Fig.1 Charging profile of battery

2.1.2 行程结束时间

由于目前缺乏电动汽车出行的相关数据，而居民出行的时间分布与车辆型号关系不大，因此采用美国交通部对于传统燃油车辆调查所得的统计数据，用于充电负荷计算。行程结束时间x近似满足正态分布，其概率密度函数如式（1）所示[16]。

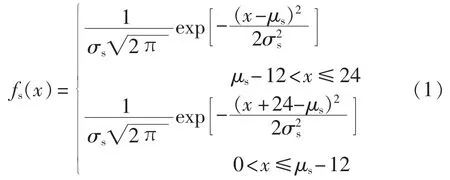
其中，μs是概率密度函数的期望值，μs=17.6；σs是概率密度函数的标准差，σs=3.4。由于95%以上车辆在10:00之后结束行程[12]，为了简化分析过程，假设所有电动汽车均在10:00后结束行程。

2.1.3 每日行驶里程

车辆每日行驶里程r近似满足对数正态分布，其概率密度函数如式（2）所示[16]：

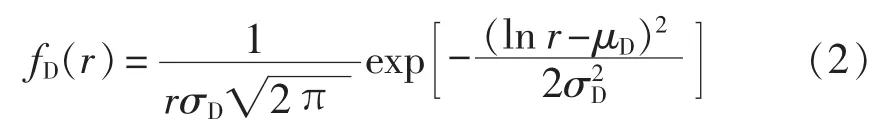
其中，μD是概率密度函数变量r的对数lnr的平均数，μD=3.2；σD是概率密度函数变量r的对数lnr的标准差，σD=0.88。

2.2 电动汽车充电负荷计算模型

如图1所示，电池从零电量至满电量需要5 h，因此将该充电过程分为5个充电阶段，每个充电阶段时长1 h。不同的起始荷电状态对应着不同的起始充电阶段，各阶段的充电功率为Pm（m=1，2，…，5），其计算式如下式所示：

其中，P（m）是图1所示充电功率曲线上第m小时的充电功率。类似地，将一天划分为24个时间段，每段时长1 h。车辆在时段t内开始充电时，假设其从t-1时刻开始充电，在时段t内电池都处于同一充电阶段。

由于电池有5个充电阶段，因此在时段i（i=1，2，…，24）内电动汽车正在充电时，该车辆将处于电池的5个充电阶段中的某一个阶段，时段i内电动汽车处于上述第m充电阶段的概率为φ（Pm，i）。

考虑分时电价后，原来在峰时段充电的电动汽车转移到谷时段充电，因此在峰时段内电动汽车处于各个充电阶段的概率减小了，而谷时段内电动汽车处于各个充电阶段的概率则增加了。考虑分时电价后，车辆在时段i内处于充电阶段m的概率改变了ΔPmri，考虑分时电价后车辆在时段i内处于充电阶段 m 的概率 D（Pm，i）的计算式如式（4）所示：

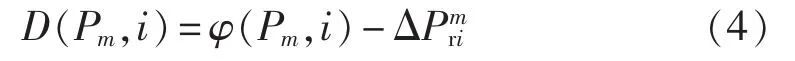
因此考虑分时电价后时段i内一辆电动汽车的充电负荷期望值为μ，计算式如式（5）所示：

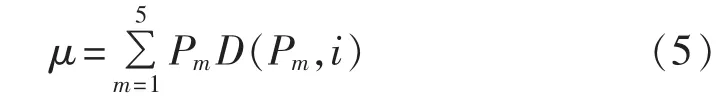
根据中心极限定理，时段i内N辆电动汽车充电负荷期望值计算式如式（6）所示：

其余时段的充电负荷期望值可以同理计算。

2.3 车辆处于各充电阶段概率的计算

无分时电价时，车辆结束行程后就开始充电。车辆在时段t内开始充电的概率FT（t）计算式如式（7）所示：

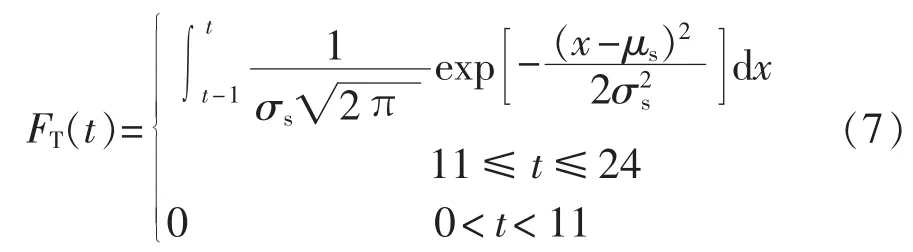
设En是根据图1所示的充电功率曲线，从第n-1时刻开始充电至电池满电量所需要的电能；e是电动汽车行驶时每千米的耗电量。当电池起始充电阶段为n，至电池充满共经历6-n个充电阶段，由于最小的时间间隔为1 h，电池实际需要的充电时间在5-n至6-n个小时之间。因此开始充电时车辆处于充电阶段n的概率Hn计算式如式（8）所示：

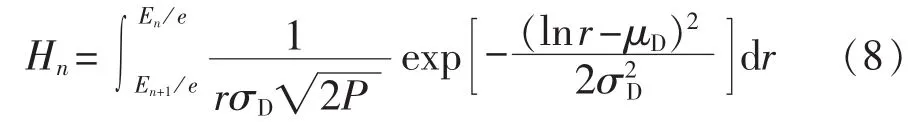
当车辆在时段 i（i=1，2，…，24）处于第 m（m=1，2，…，5）充电阶段时，可能对应着m个不同的充电过程，每个充电过程中车辆在起始时段处于第n（n=1，2，…，m）充电阶段，开始充电时段为 i-（m-n）。在时段i内电池处于其第m充电阶段，即充电功率为 Pm的概率 φ（Pm，i）计算式如式（9）所示：

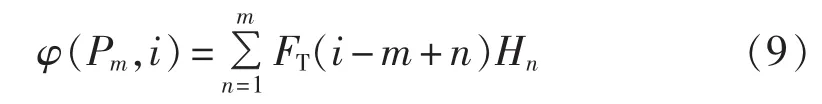
其中，FT（i-m+n）是车辆在时段i-m+n开始充电的概率；Hn是开始充电时处于第n充电阶段的概率。同理可求出该时段内车辆处于其他充电阶段的概率以及其他时段内车辆分别处于5个充电阶段的概率。

2.4 车辆处于各充电阶段概率改变值的计算

2.4.1 电动汽车对分时电价的响应

由于分时电价所规定的峰时段电价比谷时段高，因此出于节省成本的考虑，车辆将尽量在谷时段充电。当电动汽车充电过程满足如下的2种情况时车辆充电过程不转移：车辆的充电过程有一部分时间在谷时段内；充电时间长于谷时段的时间长度。除此2种情况外，在峰时段充电的车辆将转移至谷时段。充电过程转移后，开始充电时车辆处于第n充电阶段（n=1，2，…，5），根据假设电池必须充满，因此充电过程转移后在时段t开始充电的概率分布如式（10）所示：

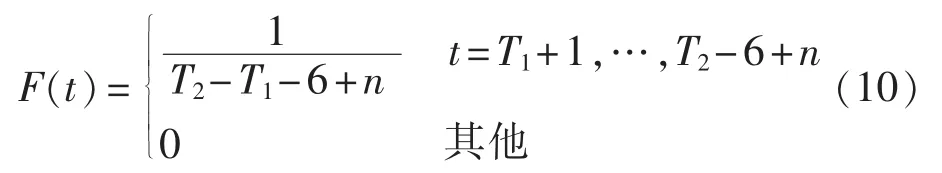
其中，T1为谷时段开始时刻；T2为谷时段结束时刻。

2.4.2 车辆处于各充电阶段概率改变值的计算

设车辆在时段 i（i=1，2，…，24）处于第 m（m=1，2，…，5）充电阶段，考虑分时电价后，车辆的充电过程发生了转移，计算转移后时段 j（j=1，2，…，24）内车辆处于第m充电阶段概率的改变值。车辆开始充电时处于第 n（n=1，2，…，m）充电阶段且在时段i内处于第m充电阶段的概率为FT（i-m+n）Hn。车辆充电过程转移后在时段j内车辆处于充电阶段m的概率等于车辆在时段j-m+n开始充电的概率，其大小等于F（j-m+n）。因此车辆充电过程转移后，车辆在时段j内处于第m充电阶段的概率增加了Prmi，j，而车辆在时段i内处于第m充电阶段的概率减少了Prmi，j，其计算式如下式所示：

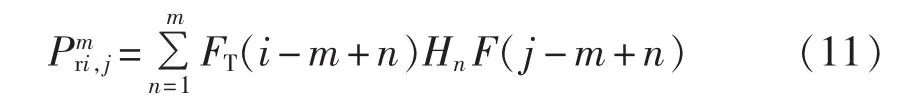
当车辆在时段j内处于第m充电阶段，开始充电时处于第n充电阶段，考虑分时电价后，充电过程发生转移，车辆在时段i内处于第m充电阶段的概率相应增加了 Prmj，i，计算式类似于式（11）。 因此，考虑分时电价后，车辆在时段i内处于第m充电阶段概率的改变值ΔPmri计算式如式（12）所示：

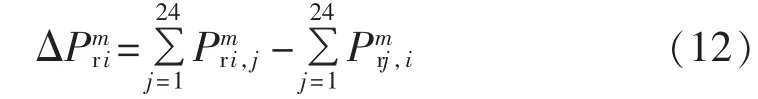
时段i内车辆处于其他充电阶段概率的改变值可以同理求出。

2.5 考虑分时电价充电负荷计算流程

考虑分时电价后，车辆充电过程转移到谷时段，车辆在各个时段内处于相应充电阶段的概率发生了改变。当求解出每个时段内车辆处于各充电阶段的概率变化值后，根据式（4）即可得到考虑分时电价后每个时段内车辆处于各充电阶段的概率，并根据式（5）、（6）计算各时段充电负荷的期望值。充电负荷计算流程如图2所示。

3 考虑分时电价充电负荷计算实例

本节将运用本文所提出的充电负荷计算方法计算10000辆电动汽车的充电负荷一天内在时间上的分布情况。如图3所示，图中所示负荷曲线是在没有分时电价调节下10000辆电动汽车充电负荷的负荷曲线。可以看到，充电负荷分布在10:00至次日04:00之间，这与前述行程结束时间基本一致。最大负荷出现在18:00，此时也是大量电动汽车结束行程开始充电的时刻。

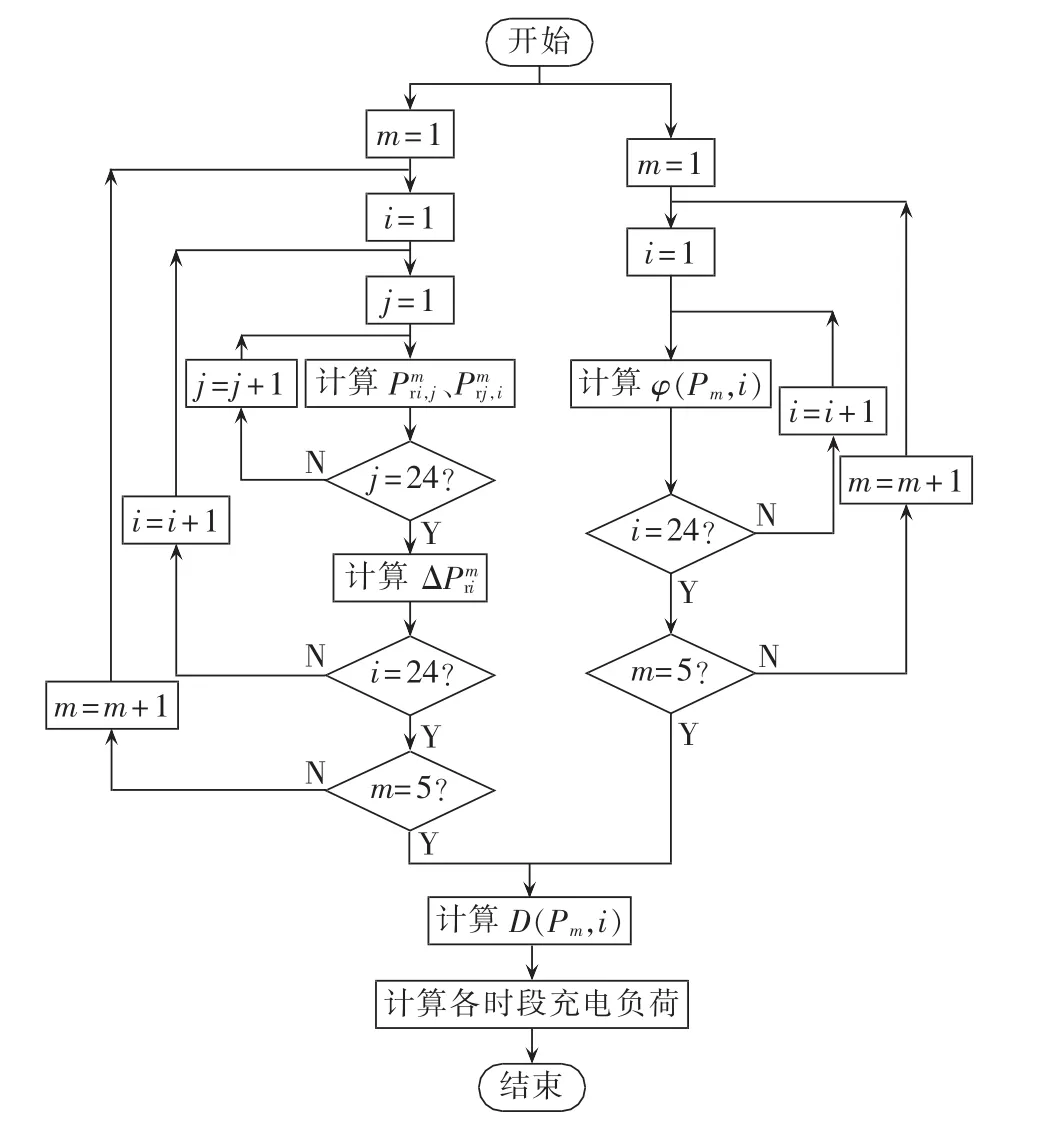
图2 考虑分时电价充电负荷计算流程图Fig.2 Flowchart of charging load calculation considering TOU

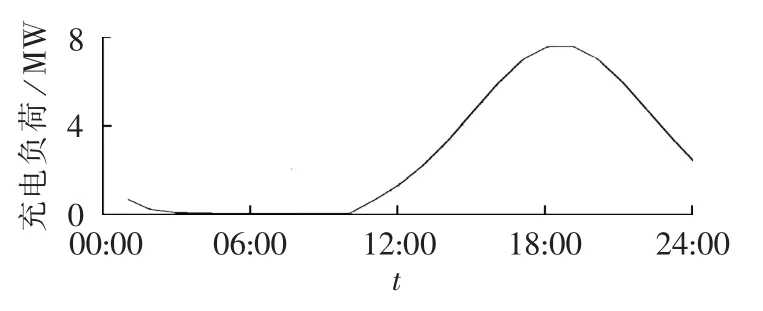
图3 不考虑分时电价充电负荷曲线Fig.3 Charging load curve without considering TOU

根据分时电价时段划分的不同，设置3个不同的场景以计算不同分时电价下的充电负荷曲线。设T1为谷时段开始时刻，T2为谷时段结束时刻，场景1 中 T1=22:00，T2=06:00，场景 2 中 T1=24:00，T2=06:00，场景 3 中 T1=02:00，T2=06:00，3 个场景下的充电负荷曲线如图4所示。在场景1、2中，充电负荷全部分布在谷时段内，场景2的最大充电负荷较场景1要高出许多，这是因为场景2中谷时段时间较短，充电负荷分布更集中。由于场景3中谷时段时间长度比电池最大充电时间要短，因此充电负荷在峰时段仍然有一定的分布，同时最大充电负荷也最高。每天凌晨以后城市的负荷曲线在荷谷时期，与考虑分时电价的充电负荷叠加后，可以起到填谷的作用，平滑负荷曲线。

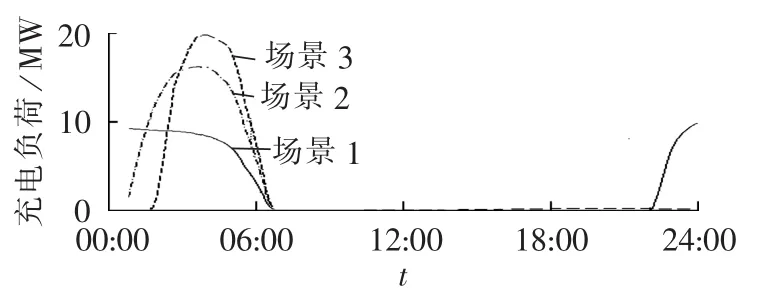
图4 不同场景下的充电负荷曲线Fig.4 Charging load curves for different scenarios

4 与其他充电负荷计算方法的比较

目前常采用蒙特卡洛模拟方法计算充电负荷分布，本节将分别采用本文方法和文献[13]中蒙特卡洛模拟方法计算T1=01:00，T2=06:00时，1 000辆电动汽车的充电负荷，蒙特卡洛模拟方法的仿真次数设为5000次，对比2种计算方法的性能。如图5所示，2种方法计算得到的充电负荷变化趋势基本一致，但每个时段的充电负荷则有一些差别。

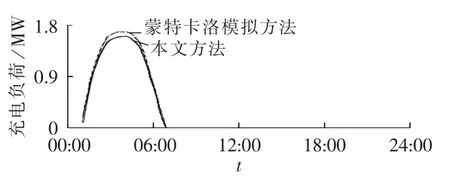
图5 2种不同计算方法的充电负荷曲线Fig.5 Charging load curves for twocalculation methods

由于利用拟合的概率密度函数计算随机变量处于有限区间内（如实际到家时间或行驶里程范围内）的概率小于1，因此理论上的概率分布与通过蒙特卡洛模拟方法得到的概率分布存在一定误差。表1及表2中所示为蒙特卡洛模拟方法（简称方法1）产生的行程结束时间及充电持续时间随机数的概率分布与本文方法（简称方法2）所采用的理论上的概率分布，可以看到2种方法所得到的概率分布有差异。

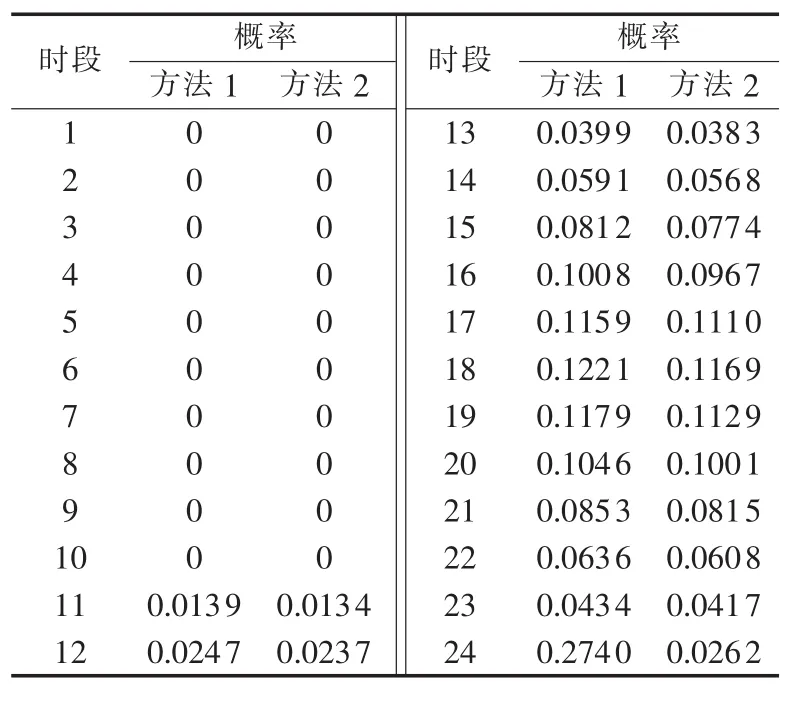
表1 2种计算方法行程结束时间概率分布对比Tab.1 Comparison of probability distribution of trip terminating time between two methods

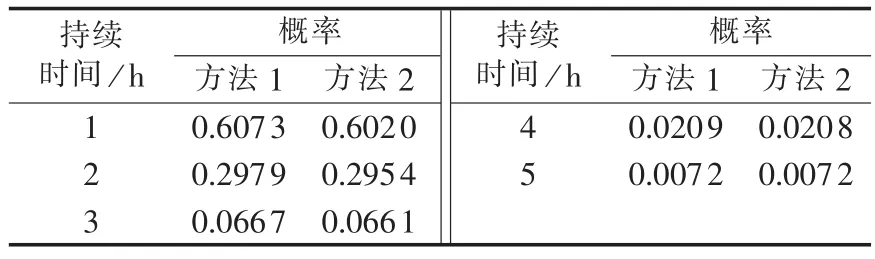
表2 2种计算方法充电持续时间概率分布对比Tab.2 Comparison of probability distribution of charging duration between two methods

图6中所示为前述场景下，根据实际随机数的概率分布采用本文方法及蒙特卡洛模拟方法计算得到的充电负荷的负荷曲线。每个时段的充电负荷计算结果对比如表3所示。从表中可以看到采用实际的随机数概率分布后，两者的计算结果基本一致，证实了前述误差产生的原因，从而验证了本文方法的正确性。

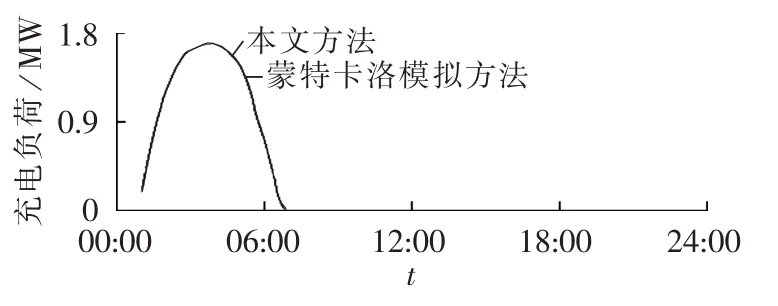
图6 改进后2种计算方法的充电负荷曲线Fig.6 Charging load curves for two improved methods

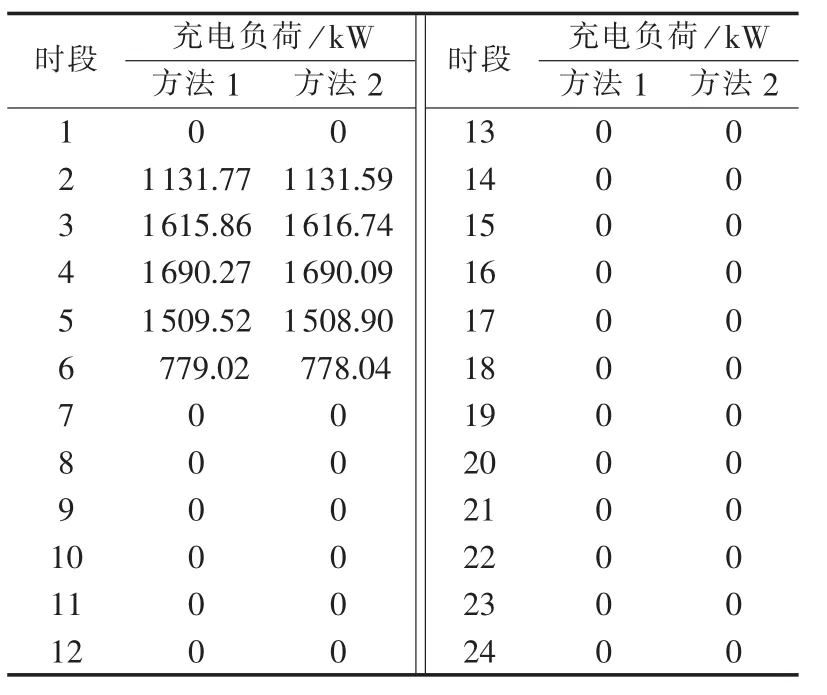
表3 改进后2种计算方法得到的充电负荷Tab.3 Charging loads calculated by two improved methods

表4为采用蒙特卡洛模拟方法及本文方法针对不同数量的电动汽车计算其充电负荷所用的时间对比。可以看出，相同数量的电动汽车，蒙特卡洛模拟方法所用时间明显长于本文方法。随着电动汽车数量的增加，蒙特卡洛模拟方法计算所需的时间在不断上升，而本文方法的计算时间基本不变。这显示本文方法计算时间与车辆数量无直接关系，对大量电动汽车入网后的充电负荷计算具有更高的计算效率。

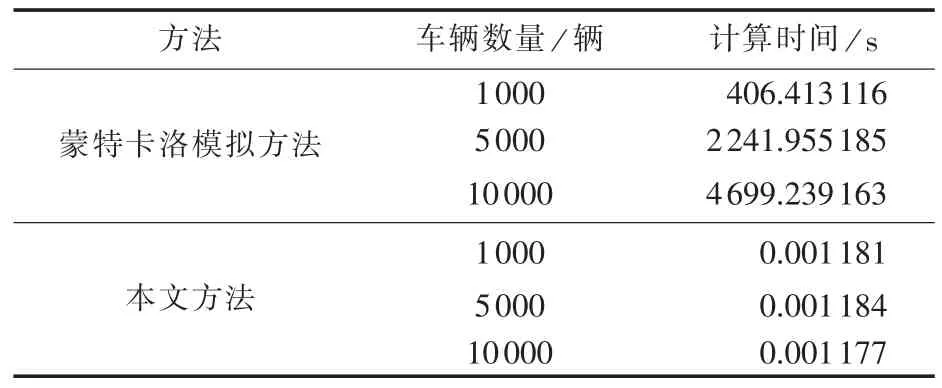
表4 2种计算方法计算时间对比Tab.4 Comparison of calculation time between two methods

5 结论

本文提出了一种新的考虑分时电价的电动汽车充电负荷计算方法，该方法将电池充电过程划分为5个阶段，计算了每个时段内电池处于各充电阶段的概率，从而得到了充电负荷在每个时段的期望值。与采用蒙特卡洛模拟方法计算充电负荷相比，该方法计算结果相近，且简化了计算过程，计算时间较少，计算效率更高，易于工程应用。该方法对于分时电价时段划分优化、量化评估现行分时电价下充电负荷对电网影响等有着重要的作用。