基于传递矩阵法的重载铁路路基基床应力及变形分析方法研究

刘晶磊，叶庆志，宋绪国，罗 强，吕文强

(1.西南交通大学高速铁路线路工程教育部重点实验室， 成都 610031；2.铁道第三勘察设计院集团有限公司，天津 300251)

基于传递矩阵法的重载铁路路基基床应力及变形分析方法研究

刘晶磊1，2，叶庆志1，宋绪国2，罗 强1，吕文强1

(1.西南交通大学高速铁路线路工程教育部重点实验室， 成都 610031；2.铁道第三勘察设计院集团有限公司，天津 300251)

目前现行规范对层状体系的铁路路基基床结构的应力应变计算采用等效厚度法，按Boussinesq公式进行计算，等效厚度法采用Odemark模量与厚度当量假定，将路基上不同模量的厚度土层折算成与路基下部填料同模量的等效层厚，该方法并没有很好反映不同土层材料性质之间的差异，对高模量的道砟层、基床表层、基床底层在路基应力场分布中的作用，缺乏严密的理论依据。针对重载铁路路基4层结构体系，采用基于传递矩阵的层状理论分析方法针对其不同深度处的应力变形求解。通过均质土层的计算结果与Boussinesq公式的理论结果的比较，验证了传递矩阵法及其计算程序可行性，最后为了进一步说明该方法的合理性，对比有限元和传递矩阵法的计算结果，结果表明，二者吻合较好。

重载铁路路基；传递矩阵法；层状体系；Boussinesq公式

1 概述

客运高速、货运重载是当今世界各国铁路发展的两大趋势，重载铁路运送能力大，经济和社会效益显著，发展铁路重载运输，已成为世界各国铁路运输发展的方向，也是我国加速提高铁路运输能力的主要途径。

在现有铁路路基设计的规范[1-3]中，动应力沿路基深度的分布，采用理论计算办法，根据采用Odemark的模量与厚度当量假定，将不同模量(模量E)的厚度h折算成与底层(模量E0)同模量的等效层厚he

进行等效厚度转换后，再根据Boussinesq公式的应力解可得矩形荷载中心点处的垂直应力，见式(2)

式中σz为矩形均布荷载中心点下z深度处的垂直应力；m=a/b，n=Z/b，2a为荷载长边，2b为荷载短边；P0为荷载强度。

对于基床结构的变形计算，首先采用上述的方法计算应力，再根据实际空间内的应力和各层的计算模量，计算各点应变，再由应变计算路基面变形。

可见，目前现行的铁路路基设计规范建议的应力、变形的计算方法均不能很好地反映实际土层间材料性质的差异。针对传统方法存在的问题，长期以来一直希望找到一种合理的简化算法，通过解析方法明确基床结构的动应力和动变形。因此，研究找出一种合理、简便、准确，适用于工程设计的方法是具有重要的工程意义的。层状土体结构以及传递矩阵法的研究[4-5]，为重载铁路路基基床结构的应力、变形计算提供了一个新的思路，可以使计算更贴近实际基床结构复杂的多层条件。

2 层状路基传递矩阵法求解应力变形

2.1 传递矩阵法基本思想

在相当广泛的一类工程问题中，比如在连续梁、传动轴系统、电路等体系中，往往存在这样的系统，这些系统可以是或可以化成由一系列具有同类性质的“元素”先后连接而成的链式系统[4]。在这个链式系统中，描写每个元素性质的一组物理量，或称为该元素的状态参量，组成该元素的状态矢量。由于各个元素之间的相互作用，因而前一个元素状态矢量的变化将影响和它相连的下一个元素的状态矢量，下一个元素状态矢量的变化又将影响下下一个元素的状态矢量，这样，初始端元素状态矢量的变化就会一直传到末端元素。设第i个元素的状态矢量是Zi，Zi是一个列向量，而第i+1个元素和第i个元素之间的相互作用往往可以用一个方阵Ti来表示，见式(3)

式中，Ti列数等于Zi的行数，而Zi的行数等于元素的状态参量的个数。如果系统由n个元素组成，则有式(4)

式中，Ti称作第i个子传递矩阵。而T称作总传递矩阵。如果把层状土体系看作一个系统，把深度z作为自变量，也就是说，初始状态向量沿深度方向传播。

这里通过传递矩阵将上下两层接触面的应力分量、位移分量联系起来，再考虑接触面的连续条件及边界条件，最终可以利用传递矩阵表示出地基表面的初始状态分量与所求深度处的应力、位移状态分量的物理关系。

2.2 4层基床结构应力及变形

针对重载路基的结构，上部荷载作用于钢轨，并通过钢轨、轨枕传递至道床表面，每根轨枕上的荷载分担比按照文献[6]的计算结果进行分配，不同轮轴作用下轨枕荷载分担比见图1。

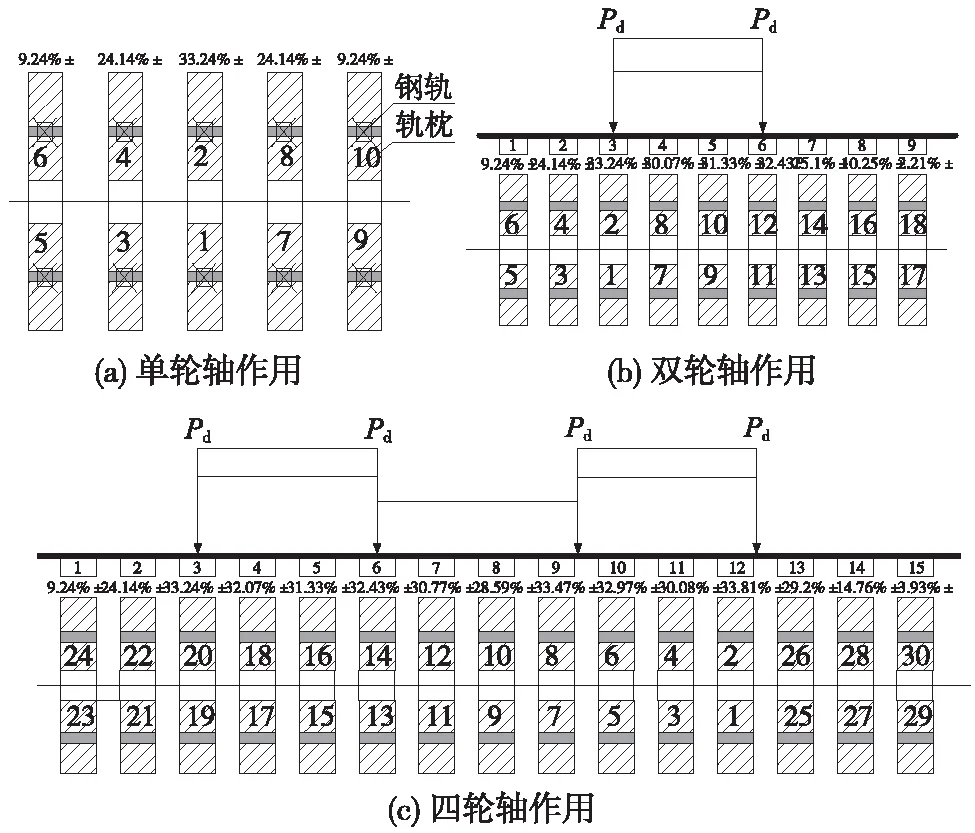
图1 轨枕上荷载分担比

施加荷载的值根据文献[3]中建议的式(5)确定，这里行车速度v取120 km/h。

式中，Pd为动轴载，kN；Ps为静轴重，kN；α为动力冲击系数或称速度影响系数，货车取0.004；v为行车速度。

进一步，设作用于道床表面的矩形荷载为p0，矩形荷载的长度和宽度分别为l和b，道床和路基共分为4层，第i层的层底埋深为zi，其层厚为hi，弹性力学参数为Ei、νi，见图2和图3。

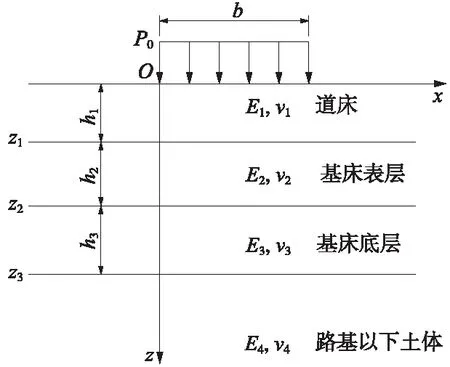
图2 4层路基结构体系受矩形荷载作用简图

图3 上部矩形荷载分布简图

各层传递矩阵T=T(E，ν，z，α)为对应层的弹性模量E、泊松比ν和深度z的函数，其元素为[7]：

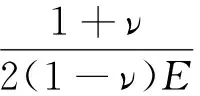
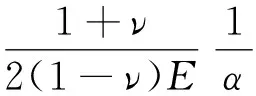
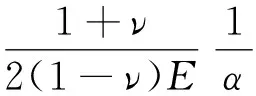
T33=T22；T34=-T12；T42=-T31；

T43=-T21；T44=T11。

4层路基结构体系总传递矩阵G，见式(6)。顶层至第k层任意深度z处的传递矩阵G′，见式(7)

(1)第1层(道床)内任意深度z(z1≥z>0)的竖向应力和竖向位移。

传递矩阵关系式，见式(8)

故矩形荷载角点下第1层(道床)内任意深度z下的竖向应力，见式(9)

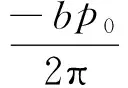
矩形荷载角点下第1层(道床)内任意深度z下的竖向位移，见式(10)

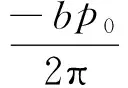
(2)第2层(基床表层)内任意深度z(z2≥z>z1)的竖向应力和竖向位移。

传递矩阵关系式，见式(11)

T2(E2，ν2，z-z1，α)×

故矩形荷载角点下第2层(基床表层)内任意深度z下的竖向应力，见式(12)

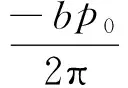
矩形荷载角点下第2层(基床表层)内任意深度z下的竖向位移，见式(13)

(3)第3层(基床底层)内任意深度z(z3≥z>z2)的竖向应力和竖向位移。

传递矩阵关系式，见式(14)

T3(E3，ν3，z-z2，α)·T2(E2，ν2，h2，α)·

故矩形荷载角点下第3层(基床底层)内任意深度z下的竖向应力，见式(15)

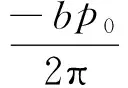
矩形荷载角点下第3层(基床底层)内任意深度z下的竖向位移，见式(16)

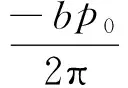
(4)第4层(基床以下土体)内任意深度z(z>z3)的竖向应力和竖向位移。

传递矩阵关系式，见式(17)

T4(E4，ν4，z-z3，α)·T3(E3，ν3，h3，α)·

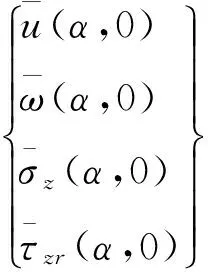
故矩形荷载角点下第4层(基床以下土体)内任意深度z下的竖向应力，见式(18)

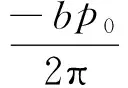
矩形荷载角点下第4层(基床以下土体)内任意深度z下的竖向位移，见式(19)

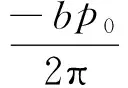
综上所述，用积分的方法求得了4层路基结构体系在矩形荷载面角点下的竖向附加应力σz(z)和竖向变形ω(z)，进一步，可以运用角点法求得矩形荷载下任意点的竖向附加应力σz(z)和竖向变形ω(z)。

3 传递矩阵法程序可行性分析

由于在计算公式中涉及到矩阵的乘法和贝塞尔函数的积分[8]，需要编制相应的计算程序计算，采用辛普森复合积分公式，利用Matlab软件编写求4层弹性半空间路基中任意一深度处矩形荷载角点下的附加应力系数和变形的程序。程序流程见图4。

图4 计算流程

为了验证上述计算程序的合理性，选择单轮轴作用、轴重25t条件下，均质土路基结构的竖向动应力进行计算，并与Boussinesq公式[9]的计算结果进行比较。这里计算所采用的几何尺寸参照文献[3]中建议的基床结构设计尺寸，道床厚0.5 m，基床表层0.6 m，基床底层1.9 m。

对于传递矩阵法的计算程序，计算参数如下：

工况①：1～4层的弹性模量E1=E2=E3=E4=180 MPa(按A组填料的弹性模量取值)[10，11]，泊松比为ν1=ν2=ν3=ν4=0.25，矩形荷载长l=1.09 m，宽b=0.32 m，任意两轨枕间中心线距0.6 m，分别计算0.5、1.1、3 m和6 m处的竖向动应力值；

工况②：1～4层的弹性模量E1=E2=E3=E4=300 MPa(按道砟的弹性模量取值)[10-11]，泊松比为ν1=ν2=ν3=ν4=0.25，矩形荷载长l=1.09 m，宽b=0.32 m，任意两轨枕间中心线距0.6 m，分别计算0.5、1.1、3 m和6 m处的竖向动应力值。

对于Boussinesq公式，计算参数主要有：矩形荷载长l=1.09 m，宽b=0.32，任意两轨枕间中心线距0.6 m，分别计算0.5、1.1、3 m和6 m处的竖向动应力值。

计算结果见表1。可见，采用传递矩阵法计算均质土路基结构时，与Boussinesq公式的计算结果吻合较好，该计算方法和计算程序是可行的。

表1 均质土路基结构竖向动应力计算结果

4 传递矩阵法和有限元计算结果比较

进一步，为了验证传递矩阵法计算结果的合理性，采用有限元法进行验证，基床结构采用线弹性材料进行模拟。有限元计算工况为：①基床表层为A组填料，轴重25 t、单轮轴作用和轴重30 t、四轮轴作用，道床(厚0.5 m)、基床表层(轴重25 t，厚0.6 m；轴重30 t，厚0.7 m)、基床底层(轴重25 t，厚1.9 m；轴重30 t，厚2.3 m)[3]以及路基以下土体弹性模量分别取300、180、110 MPa和60 MPa[10，11]，泊松比取0.25。②基床表层为级配碎石，轴重27 t、双轮轴作用和轴重35 t、四轮轴作用，道床(轴重27 t，厚0.35 m；轴重35t，厚0.4 m)、基床表层(轴重27 t，厚0.6 m；轴重35 t，厚0.7 m)、基床底层(轴重27 t，厚1.9 m；轴重35 t，厚2.3 m)[3]以及路基以下土体弹性模量分别取300、240、110 MPa和60 MPa[10-11]，泊松比取0.25。有限元分析模型见图5。

图5 有限元计算模型

将有限元计算结果与传递矩阵法的计算结果进行比较，应力比较的结果见表2和表3，路基面变形的比较见表4。由表2、表3及表4可以看出，无论是应力的绝对值、相对值，还是路基面的变形值，两种方法的计算结果相比存在一些细微的差异，主要是由于两种方法的边界条件存在一些差异，对于传递矩阵法，在线路纵向是无限的，不存在边界，而有限元法在线路纵向是有边界限定的。但是从整体上来看，两种方法的计算结果基本吻合较好。

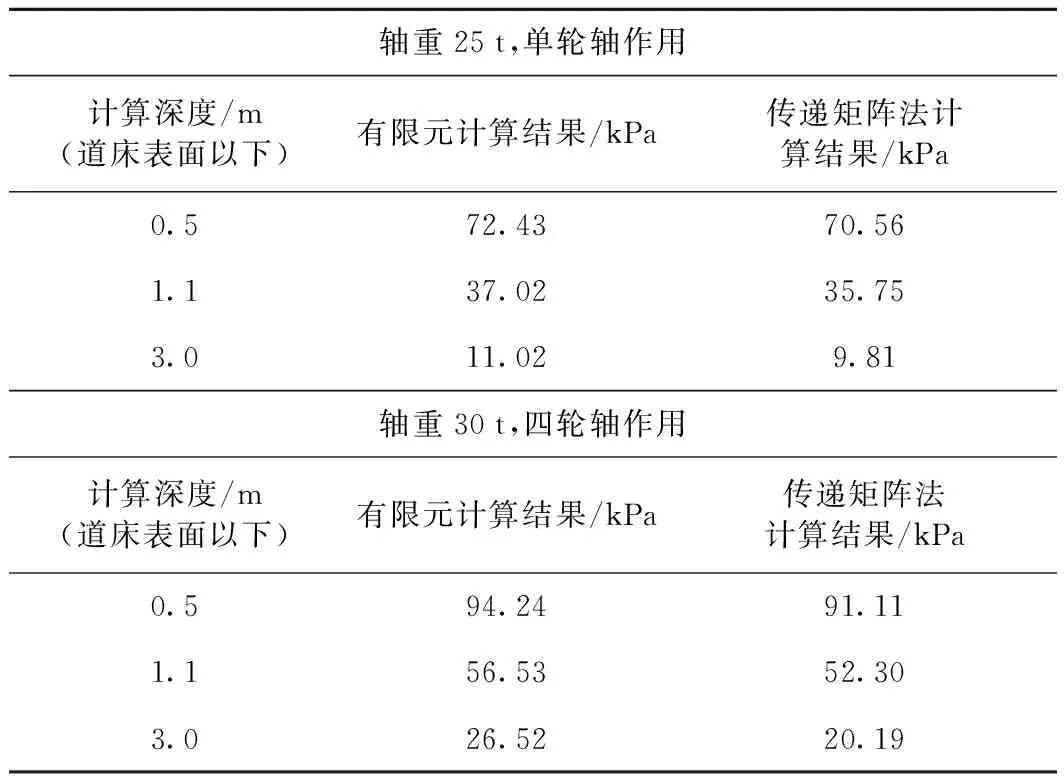
表2 计算结果(应力)的比较(基床表层为A组填料)

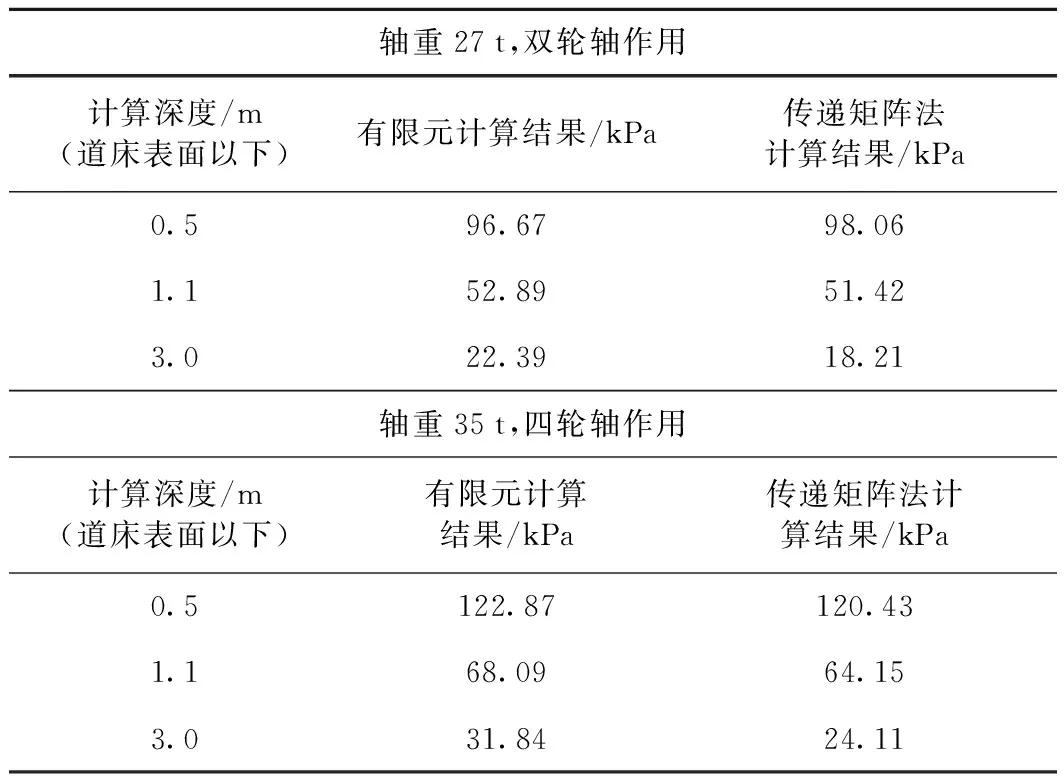
表3 计算结果(应力)的比较(基床表层为级配碎石)

进一步，将传递矩阵法和有限元法的计算结果与铁科院在朔黄铁路的测试结果[12](该测试进行了轴重25、27 t以及30 t的实车试验)进行比较。现场实测路基面的动应力值为40～120 kPa，计算结果在测试范围之内。对于路基面的动变形，测试结果为1.5～2 mm，两种计算方法的结果与测试结果相近。

表4 计算结果(路基面的变形)的比较 mm

5 结论

建议了一种基于传递矩阵法的4层路基结构体系计算方法，该方法力学、数学思路明确，计算方法简便，适合于工程实际应用，易于推广。通过对均质土路基结构进行计算，并与Boussinesq公式的计算结果进行比较，结果吻合较好。进一步，采用该方法对重载铁路路基结构进行计算，并与有限元法的计算结果进行比较，结果吻合较好，计算精度符合工程实际需求。

[1] 铁道第三勘察设计院集团有限公司， 中铁第四勘察设计院集团有限公司，中国铁道科学研究院.BT10621—2009 高速铁路设计规范[S].北京:中国铁道出版社，2009.

[2] 铁道第一勘察设计院.TB10001—2005 铁路路基设计规范[S].北京:中国铁道出版社，2005.

[3] 铁道第三勘察设计院集团有限公司.重载铁路设计规范(报批稿)[S].天津:铁道第三勘察设计院集团有限公司，2011.

[4] 王凯.层状弹性体系的力学分析与计算[M].北京:科学出版社，2009.

[5] 姚炳卿.多层弹性体系力学分析中积分常数计算的矩阵分析方法[J].计算结构力学及其应用，1992(2):163-170.

[6] 西南交通大学.轴重30 t黄泛区重载铁路路基动力特性分析和施工技术研究[R].成都:西南交通大学，2013.

[7] 罗世毅.水平层状地基中附加应力与沉降计算分析[D].西安:长安大学，2003.

[8] 徐常伟，于凯，朱峰.基于李群方法的贝塞尔函数数学实现[J].纯粹数学与应用数学,2013，29(3):275-281.

[9] 陈仲颐.土力学[M].北京:清华大学出版社，2007.

[10] 董亮，张千里，蔡德钩.高速重载有砟轨道路基动变形特性的数值分析[J].中国铁道科学,2010，31(2):6-11．

[11] 董亮，赵成刚.高速铁路路基的动力响应分析方法[J].工程力学,2008，25(11):231-236.

[12] 中国铁道科学研究院.轴重30 t以上煤炭运输重载铁路关键技术与核心装备研制——重载线路基础设施强化措施研发[R].北京：中国铁道科学研究院，2013.

Study on Stress and Deformation Analytic Method of Heavy Haul Railway Subgrade Based on Transfer-matrix

LIU Jing-lei1，2， YE Qing-zhi1， SONG Xu-guo2， LUO Qiang1， LU Wen-qiang1

(1.MOE Key Laboratory of High-speed Railway Engineering， Southwest Jiaotong University， Chengdu 610031， China; 2.The Third Railway Survey and Design Institute Group Corporation， Tianjin 300251， China)

The stress and strain of railway subgrade of layered system are calculated with Boussinesq formula in equivalent thickness method as per the current standard. Odemark modulus and thickness equivalent assumption are applied in the equivalent thickness method， the thickness of the soil layer with different moduli above the subgrade is converted into equivalent thickness of the same modulus of the subgrade filler， but this method can not truly reflect the difference between the properties of different soil materials， and the functions in the stress field distributions contributed by the ballast layer with high modulus， the bedding surface layer and the bedding bottom layer are not supported by rigorous theoretical basis. For four layers structure system of the heavy haul railway， the layered analytic method theory is used to calculate the stress and deformation at different depth based on transfer-matrix. The comparison of the theoretical results of the Boussinesq formula with the calculation results of homogeneous soil layer verifies the feasibility of the transfer-matrix method and its calculation program. Finally in order to illustrate the rationality of this method， the result of the finite element are compared with that of the transfer-matrix method， and the two methods prove to be in good agreement with each other．

Heavy haul railway subgrade; Transfer-matrix method; Layered system; Boussinesq formula

2014-07-01

国家科技支撑计划项目(2013BAG20B00)，国家973计划课题(2013CB036204)

刘晶磊(1981—)，男，博士后，E-mail:kingbest_1118@163.com。

1004-2954(2014)09-0014-06

TU47

：A

10.13238/j.issn.1004-2954.2014.09.004