基于平均导数方法的声波方程频率域高阶正演

张衡，刘洪，刘璐，金维浚，史小东

1中国科学院地质与地球物理研究所 中国科学院油气资源研究重点实验室，北京 100029

2中国科学院大学，北京 100049

1 引言

频率域正演是频率域全波形反演的基础（Virieux and Operto，2009；刘璐等，2013b），它最早是用有限元的方法来实现的，由Lysmer和Drake（1972）提出用于模拟地震波传播并由 Marfurt（1984）和Shin（1988）进一步发展.Pratt（1990）将有限差分算法用于频率域正演中来进行跨孔层析成像和地震波形反演的研究.

频率域正演的优势在于多个频率可以单独模拟，适于多炮同时模拟，且不存在累积误差.在频率域中正演问题演变成对于每个给定的频率求解大型稀疏线性方程组的问题，一般需要较大的内存存储空间，尤其是在三维频率域大尺度模拟中大型矩阵往往不易求解，从而限制了三维频率域全波形反演的应用（Operto et al.，2007）.

以相速度误差1%为标准，Pratt和 Worthington（1990）提出的5点声波频率域正演算法需要每个波长13个网格点才能正确模拟，计算精度差.为了解决这个问题，Jo等（1996）提出了旋转坐标系的9点格式来求解标量波动方程，引入45°旋转坐标系和原水平直角坐标系组成的混合网格来近似拉普拉斯算子，并对加速度项进行加权平均，采用优化方法求取优化系数.这种优化9点混合网格差分格式能使得每个波长所需要的网格点数在1%的误差范围内降低到4个网格点数，明显提高了计算精度.Shin和Sohn（1998）随后将这种方法扩展到4阶25点格式，能使得每个波长所需要的网格点数在1%的误差范围内降低到2.5个网格点数.曹书红和陈景波（2012）推导的17点格式在常规四阶9点格式的基础上引入了45°方向的旋转坐标系，可将一个波长内所需的网格点数降低到2.56个.刘璐等（2013a）则从减小系数矩阵带宽的角度出发推导得到15点格式，在减小带宽的同时保持了相当的计算精度，从而提高了计算效率.

但是，Jo等（1996）提出的混合二阶9点格式只适用于横纵向等间隔情况，这在实际波场模拟中受限很大.针对旋转坐标系的局限性，Chen（2012）利用平均导数方法（ADM）提出了二阶九点格式频率域正演方法.该方法将声波频率域方程中空间导数项的差分近似表示为正交方向上3个网格点的加权平均形式，能适用于不同的方向的空间采样间隔，因此能够作为二阶精度频率域有限差分正演的一般格式，增加了方法的灵活性并拓展了应用范围.Chen（2012）的平均导数二阶9点算法能将每个波长所需的网格点数降低到4个网格点数，但是二阶的精度仍然较差，因此需要发展高阶的算法.为了降低逆矩阵的带宽和存储量，在保持精度较高的情况下导数的差分逼近需要阶数尽可能的低，因此本文选择四阶算法开展研究.

本文首先介绍了四阶常规频率域正演算法和旋转坐标频率域正演算法，讨论了四阶情况下旋转坐标系的局限性并做了证明.针对传统四阶格式的局限性，在 Chen（2012）二阶平均导数方法（ADM）的基础上提出四阶频率域ADM 25点有限差分正演差分格式，并证明这种方法能作为高阶频率域正演的一般格式，四阶常规格式和经典的四阶25点混合格式都可以作为这种方法的一种特例.随后通过最小二乘方法求取优化系数并做了频散分析，表明ADM 25点算法能够将每个波长所需的网格点数降低到2.78个，相比二阶平均导数格式和四阶常规格式明显提高了计算精度.最后，结合PML吸收边界条件进行数值模拟，模型测试表明ADM 25点算法能对不同横纵向间距的模型进行高精度模拟.

2 传统四阶差分格式及其局限性

频率域二维标量波动方程可写为

其中，P是位移分量，ω是角频率，v为速度.

二阶声波频率域正演精度低，数值频散严重，需要较小的网格间距.而四阶正演能提高正演的精度并降低数值频散.传统四阶差分格式有常规四阶9点差分格式和混合四阶25点差分格式.

将式（1）中的二阶空间导数项写成常规四阶差分的形式即可得到如下的四阶常规9点差分格式，图1a为这种差分格式的示意图.

图1 （a）四阶常规9点差分格式示意图；（b）四阶混合网格25点差分格式示意图；（c）四阶ADM 25点差分格式示意图Fig.1 （a）Fourth-order conventional nine-point scheme；（b）Fourth-order mixed grid 25-point scheme；（c）Fourth-order ADM 25-point scheme

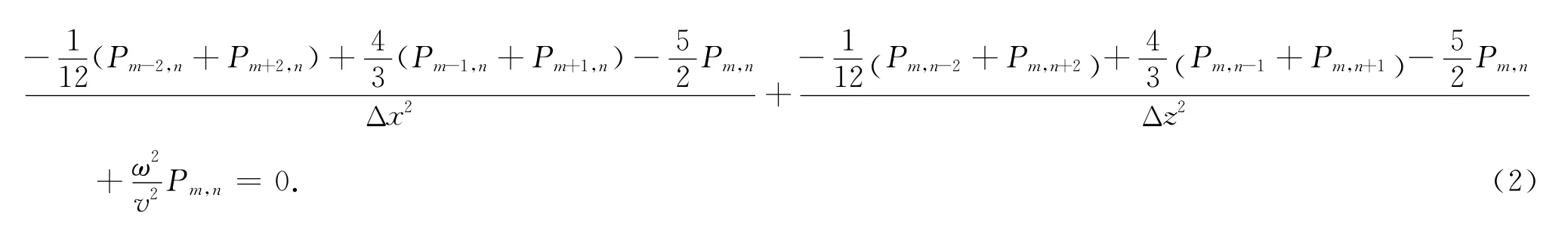
引入旋转坐标系构建混合网格的思想是由Jo等（1996）首先提出来的，Jo引入旋转坐标系构建了9点的二阶混合网格差分格式，Shin和Sohn（1998）将之推广到四阶，构建了25点格式.将45°、26.6°、63.4°旋转坐标系引入四阶9点常规网格差分格式构造，即可得到25点混合网格差分格式，图1b为这种差分格式的示意图.

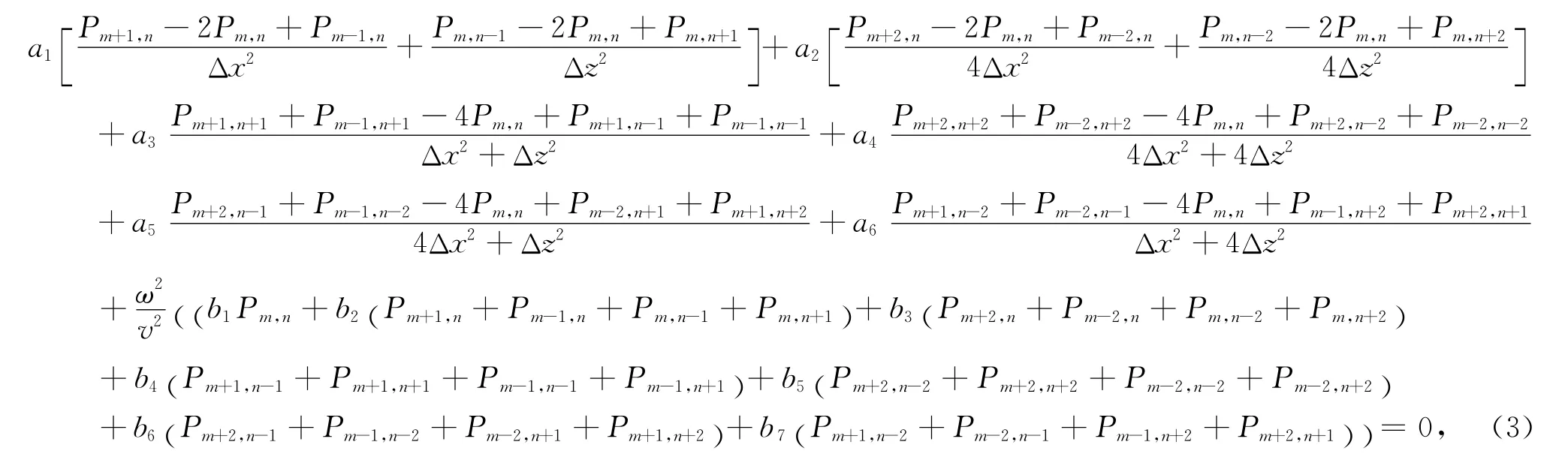
其中

式（3）前两项即为常规9点差分离散是拉普拉斯项的形式，后四项即为由不同旋转坐标系产生的高阶差分离散项，后四项通过泰勒公式展开并化简得到：

从式（4）—（7）可以看出，只有当Δx=Δz时上述四项才能成为拉普拉斯项的近似，此时：

而当Δx≠Δz时混合25点格式并不成立，这就是混合25点格式的局限性，这种局限性正是由其为了提高精度所引入的旋转坐标系所导致的（证明见附录A）.推及开去，Shin和Sohn（1998）的混合25点格式引入了三个角度的旋转坐标系，而曹书红和陈景波（2012）引入的声波四阶17点格式做了简化，只将45°的坐标系引入到常规9点格式，但是由于其仍然是基于旋转坐标系构建的差分格式，因此也只能适用于Δx=Δz等间隔的情形.

Shin和Sohn（1998）指出常规9点差分格式要求每个波长内所需的网格点数为5个，精度较低，而混合25点网格则能将每个波长内所需的网格点数降低到2.5个，相比常规9点差分格式而言提高了数值模拟的精度.但是从以上分析可知，混合25点格式的局限性在于只适用于Δx=Δz等间隔的情形，而并不适用于Δx≠Δz不等间隔的情形，而常规9点格式虽然适用于Δx≠Δz不等间隔的情形，但是精度较低.

3 基于平均导数方法的声波方程频率域四阶25点格式

由于实际应用中经常会出现横向和纵向不等间隔的情况，此时基于旋转坐标系的混合网格虽然精度较高，但是不再适用，因此需要提出一种新的既能不受间隔限制从而具有广泛适用性又精度较高的频率域正演算法.基于Chen（2012）的平均导数法构建差分格式的思路，本文构建得到四阶25点声波ADM有限差分格式（图1c）.

对式（1）频率域二维标量波动方程中的空间导数项和加速度项分别引入加权优化系数，空间导数项的四阶差分近似的波场值表示为正交方向上5个网格点波场值的加权平均形式，而加速度项则表示为ADM 25点差分格式中所有25点的加权平均.据此构建得到的四阶25点ADM有限差分格式为

其中

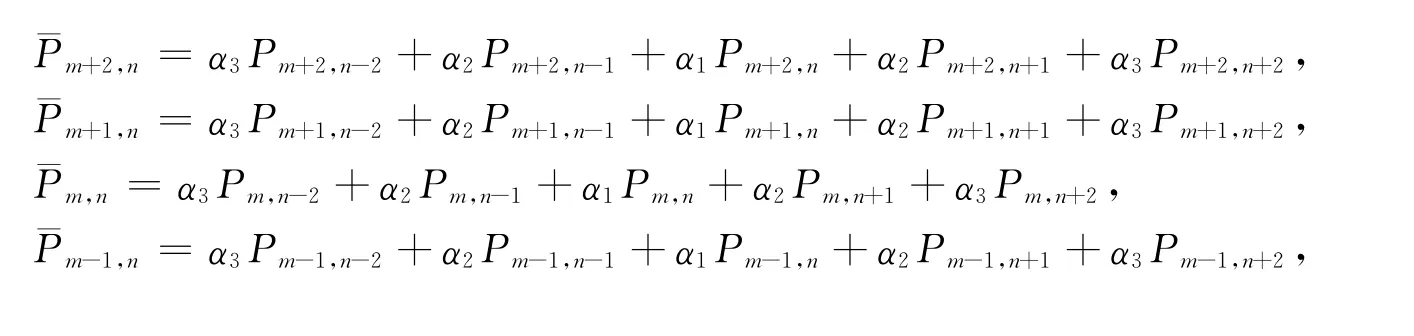
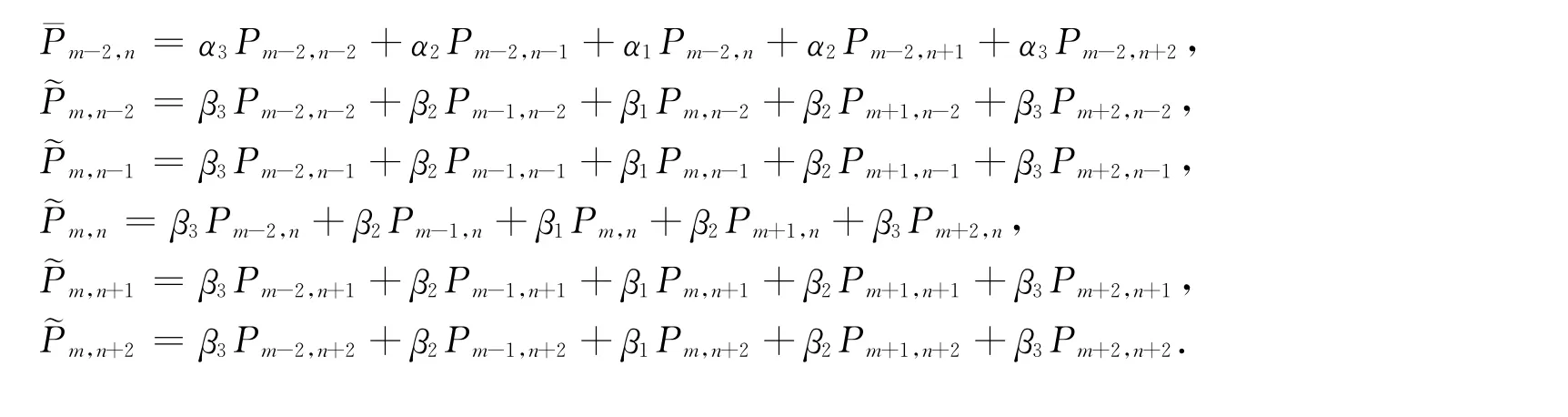
式 （8）中 α1、α2、α3、β1、β2、β3、b1、b2、b3、b4、b5、b6、b7、b8、b9是加权系数，且有如下关系：

当α1=β1=1，α2=β2=0且b1=1，b2=b3=b4=b5=b6=b7=b8=0时ADM差分格式（8）可写成公式（2）的形式，即常规9点差分是ADM 25点格式的特例.而当Δx=Δz=Δ，α1=β1，α2=β2，α3=β3时ADM差分格式（8）可写成公式（3）的形式，即混合25点差分也是ADM 25点格式的特例.

因此ADM方法不仅适用于Δx=Δz等间距的情况，也适用于Δx≠Δz的情况，而很多实际复杂模型都往往不是等间距的，因此ADM方法是一种相比常规网格和混合网格更一般性的方法，能适用于不同的网格间距，具有广泛的适用性.将ADM从二阶推到四阶，改善了数值频散，提高了计算精度，从而达到了声波频率域的高精度模拟.

4 系数优化与频散分析

采用经典的频散分析方法，引入一个平面波表示P（x，z，ω）=P0e-i（kxx+kzz）来进行频散分析的研究.

将平面波P（x，z，ω）=P0e-i（kxx+kzz）代入 ADM差分格式即式（8），求得相速度频散关系式如下：

其中

代人式（9）即可得到Δx≥Δz情况下的相速度频散关系式：

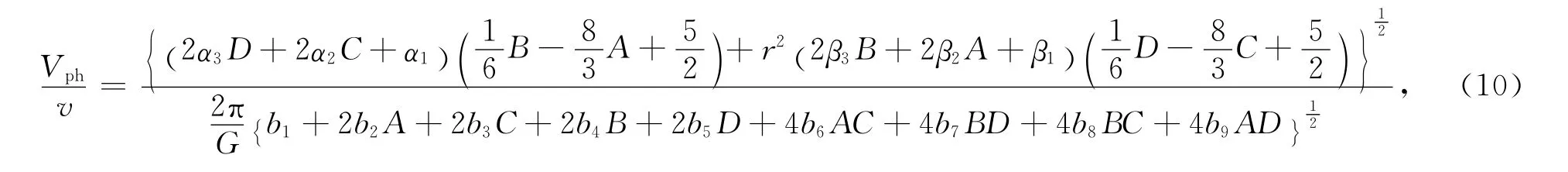
其中

令α1=β1=1，α2=β2=0，且b1=1，b2=b3=b4=b5=b6=b7=b8=0时即可得到常规9点差分的相速度频散关系式：

本文通过最小二乘方法来求取ADM 25点格式的优化系数.求取系数时令1／G的取值范围为 ［0，0.4］，间隔取为0.0001，传播角度θ的传播范围取为角度间隔取为1°，采用最小二乘的方法求取的不同情况下的优化系数如表1所示（以， ， ，， ，，r=11.21.522.533.125为例）.

表1 当Δx≥Δz时对于不同r=求得的优化系数Table 1 Optimization coefficients for different r=whenΔx≥Δz

表1 当Δx≥Δz时对于不同r=求得的优化系数Table 1 Optimization coefficients for different r=whenΔx≥Δz

优化系数 r=1 r=1.2 r=1.5 r=2 r=2.5 r=3 r=3.125 α1 0.991997726 0.805233989 0.619957247 0.413925303 0.373903717 0.394354979 0.407408592 α2 0.009593831 0.112399090 0.205383107 0.381893427 0.476554836 0.596182744 0.633290989 α3 -0.005592694-0.013647785-0.013944500-0.090884052-0.163637558-0.293022734-0.336605396 β1 0.991997726 1.060121932 1.118246442 0.876284789 0.786932676 0.697703728 0.675165649 β2 0.009593831-0.023780585-0.054965284 0.087325937 0.134458446 0.181993685 0.194014042 β3 -0.005592694-0.007364847-0.004827885-0.025008643-0.027916654-0.030889070-0.031642021 b1 0.889849126 0.864910920 0.865809648 0.751500449 0.717526005 0.674541008 0.662508511 b2 0.023342617 0.039022204 0.043656325 0.101934600 0.126218557 0.156146763 0.164567318 b3 0.023342617 0.037842560 0.041959903 0.088981227 0.102441283 0.121283998 0.126658830 b4 -0.014507490-0.015400714-0.015821289-0.020612454-0.025805466-0.033875380-0.036452751 b5 -0.014507490-0.015905813-0.018837732-0.010689362-0.007258385-0.004748004-0.004141499 b6 0.022740682 0.011553916 0.004760254-0.017542515-0.029133236-0.043937436-0.048151536 b7 0.000889472-0.000391572-0.001168792-0.000068165-0.000872688-0.002058724-0.002438015 b8 -0.003009849-0.001596517 0.000121029 0.002365050 0.005485087 0.010580676 0.012228197 b9 -0.003009849 0.000401680 0.003963411-0.002820826-0.002843110-0.002736470-0.002684763

图2分别给出了ADM 25点格式和常规9点格式在不同r=Δx／Δz情况下根据表1求取的优化系数计算得到的频散曲线.通过频散曲线分析得出，常规9点格式当G大于5的时候相速度误差才能控制在±1%以内，而达到同样的误差精度ADM 25点格式只需要G=2.78，ADM 25点格式的频散误差小于常规9点格式的频散误差，即ADM 25点格式精度更高.

为验证ADM 25点格式系数分别在Δx≥Δz和Δz＞Δx两种情况下的几何对称性，以r=Δz／Δx=2.5为例，将Δx和Δz对应项的系数互换，从r=Δx／Δz=2.5得到r=Δz／Δx=2.5的优化系数：

α1=0.786932676， α2=0.134458446，

α3=-0.027916654， β1=0.373903717，

β2=0.476554836， β3=-0.163637558，

b1=0.717526005， b2=0.102441283，

b3=0.126218557， b4=-0.007258385，

b5=-0.025805466， b6=-0.029133236，

b7=-0.000872688， b8=-0.002843110，

b9=0.005485087.

图3为根据这些优化系数求得的频散曲线及与常规9点格式在r=Δz／Δx=2.5情况下的相速度频散曲线对比图，分析得出ADM 25点格式只需要每个波长2.78个网格点就能将数值频散误差限制到1%以内，因此可以根据ADM 25点格式系数的几何对称性从Δx≥Δz情况直接得到Δz＞Δx情况的优化系数.

5 数值模拟与分析

5.1 构建ADM 25点格式PML波动方程

吸收边界条件的效果极大地影响正演模拟求解的效果，因此采用一个好的吸收边界条件非常重要.目前应用的吸收边界条件包括单程波旁轴吸收边界条件和衰减吸收边界条件两大类，Pratt（1990）和Chen（2012）在频率域模拟中采用了Clayton和Enquist（1977）的45°单程波旁轴吸收边界条件，Shin（1995）提出了添加阻尼层的频率域海绵吸收边界条件，但是这些吸收边界条件在实际应用时边界吸收效果较差.为了更好地吸收边界反射，本文数值模拟边界处理时采用目前应用效果最好的PML吸收边界条件来消除人工边界反射.PML是一种衰减型的吸收边界条件，最早由Berenger（1994）提出.本文采用二维频率域标量PML声波波动方程，并构建得到适于ADM 25点格式的PML波动方程.

图2 当Δx≥Δz时对于不同r=Δx／Δz常规四阶9点格式和四阶ADM 25点格式相速度频散曲线图：左图为常规四阶9点格式相速度频散曲线图；右图为四阶ADM 25点格式相速度频散曲线图Fig.2 Phase velocity curves of the conventional Nine-point scheme and ADM 25-point scheme for different r= Δx／Δz whenΔx≥Δz：Left figure is the phase velocity curves of the conventional Nine-point scheme and The Right figure is the ADM 25-point scheme

二维频率域标量PML声波波动方程可写为（任浩然等，2009）

式（12）结合ADM 25点差分公式即式（8）得到ADM 25点格式的PML波动方程如下：

式中

从而得到系数矩阵M的形式：

根据速度模型不同的纵横向采样间隔求得的优化系数，结合构建的ADM 25点格式PML波动方程，即可实现ADM 25点格式频率域数值模拟.下面通过一个简单均匀模型和复杂Marmousi模型来分析ADM 25点格式在不同纵横向采样间隔情况下的正演精度和正演效率，常规四阶9点算法和ADM 9点算法因为也能适用于不同的网格间隔，作为对比方法进行比较.

5.2 均匀模型测试

均匀模型的单道记录能更好地测试不同格式数值频散的效果及计算精度.取模型为200×200的网格数，取波速为2000m·s-1的一个均匀模型（图4）.数值模拟时，雷克震源子波主频取20Hz，震源位置设置在模型的中心，单检波点取在震源位置左侧50个网格点处.

均匀模型测试采用常规9点格式和ADM 25点格式进行频率域正演模拟并与解析方法进行对比，解析解采用下面公式（Alford et al.，1974）：

其中，F（ω）为频率域震源，H0（2）为零阶二类Hankel函数，r为观测点到震源点的距离.

图4 均匀模型示意图Fig.4 Sketch map of homogeneous velocity model

第一种情况设横向网格间距为9.6m，纵向网格间距为8m，此时横向纵向网格间距比为1.2，传播时间0.6s，时间采样间隔为2ms.分别采用常规9点格式和ADM 25点格式进行频率域正演模拟，横向纵向网格间距比为1.2情况下的ADM 25点差分格式优化系数如表1所示.取常规9点格式和ADM 25点格式两种格式的单道记录并与解析方法进行对比（图5a），如图在这种情况下两种格式都能精确模拟，都没有出现数值频散误差，且与解析解对应良好.第二种情况如果将横向网格间距和纵向网格间距分别增大到13.2m和11m，横向纵向网格间距比保持1.2不变，除传播时间增加到0.8s外，其他参数不变.分别取常规9点格式和ADM 25点格式两种格式的单道记录并与解析方法进行对比（图5b），此时ADM 25点的单道记录几乎没有频散与解析解对应良好，而常规9点的单道记录出现了很严重的频散，与解析解相比出现较大误差.这是由于两种方法数值模拟精度差异较大而导致常规9点格式在大网格间距下数值频散误差较大，而ADM 25点仍能保持高精度.具体而言由于常规9点格式达到无频散模拟所需的每个波长网格点数为5个，则最大网格间距大概为2000／40／5=10m，而ADM 25点格式达到无频散模拟所需的每个波长网格点数仅为2.78个，则最大网格间距可达到2000／40／2.78=18m，因此对于第一种情况，横纵向最大网格间距为9.6m，此时两种格式都能精确模拟，而对于第二种情况，横纵向最大网格间距为13.2m，已经超过了常规9点格式精确模拟所允许的10m间距，因此产生了比较严重的数值频散，而ADM 25点格式仍能精确模拟.

5.3 Marmousi模型测试

下面采用较复杂的Marmousi模型来进行模拟.标准Marmousi模型横向网格间距为12.5m，而纵向网格间距为4m，横纵向网格间距比达到了3.125，而且 Marmousi模型是一个非均匀复杂模型，能进一步测试ADM 25点算法的精度和效率.本文截取了Marmousi速度模型网格大小为301×301的一个区域（图6a）.数值模拟时，雷克震源子波主频取15Hz，震源位置设置在纵向第11层的横向40个网格点处，坐标为（500m，40m），检波点排列置于地表，每个网格点设置一个检波器，全排列共301个检波器，PML层数设为40层，传播时间为2 s，时间采样间隔为0.004s.

分别采用常规9点格式、ADM 9点格式和ADM 25点格式进行频率域正演模拟，横向纵向网格间距比为3.125情况下的ADM 25点差分格式优化系数如表1所示.从15Hz的单频波场切片（图6b）可以看出，在左侧速度渐变带，频率域波场变化不大，而在中间和右侧速度变化复杂，入射波和反射波的相互干涉导致了反射界面上频率域波场的剧烈扰动.将频率域波场通过反傅里叶变换转换到时间域得到时间域的波场快照和地表检波器采集的地震记录.从常规9点格式的地震记录（图6c）、ADM 9点格式的地震记录（图6d）以及ADM 25点格式的地震记录（图6e）对比可以清晰看出，ADM 25点能精确模拟，而常规9点和ADM 9点都出现了较强的数值频散（如图6（c，d，e）黑色箭头标示），因此常规9点格式和ADM 9点格式在横纵向网格间距不一致的情况下波场模拟精度差，相较本文方法更容易出现数值频散误差，本文方法体现出在克服数值频散误差方面的优越性.另外从地震记录上来看PML吸收边界条件的引入很好地消除了人工边界反射（图6（c，d，e））.通过与图6f中时间域12阶高阶有限差分方法（Yan and Liu，2013）的结果进行对比，验证了本文方法与时间域高阶方法精度相当.

对Marmousi模型相同计算区域同等计算精度下做了一个计算效率测试，计算平台为联想Think Centre M8300t台式机电脑（酷睿i7八核，3.4GHz）.单炮测试结果为常规9点格式频率域单炮模拟耗时8427s，ADM 9点格式频率域单炮模拟耗时3650s，而ADM 25点格式频率域单炮模拟耗时2772s.因此在相同的精度要求下，ADM 25点的计算效率要高于ADM 9点，并明显高于常规9点，这是由于ADM 25点格式精度相比常规9点格式和ADM 9点方法提升明显，因此可以通过采用更大的网格间距来提高计算效率.需要特别说明的是，更高阶的频率域正演方法带来的精度提升空间有限，并不能显著提升计算精度，反而因为系数矩阵带宽增加会明显增加计算成本，降低计算效率.

就内存存储空间而言，如果常规9点格式需要nx×nz（nx和nz分别为横向和纵向网格点数）个网格点来存储系数矩阵，则ADM 9点格式需要个网格点，本文的ADM 25点格式只需要个网格点.因此ADM 25点格式耗费的内存存储空间要少于常规9点和ADM 9点，从而减少了存储要求.

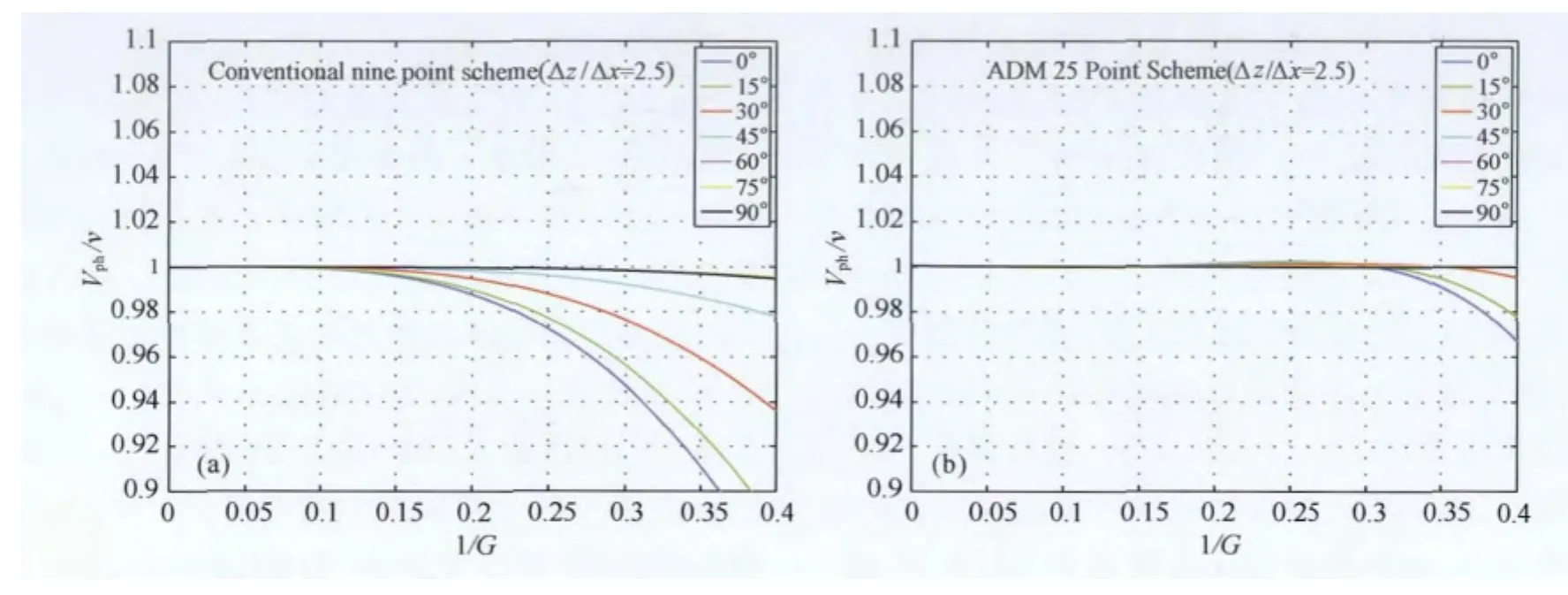
图3 当r=Δz／Δx=2.5时常规四阶9点格式和四阶ADM 25点格式相速度频散曲线图Fig.3 Phase velocity curves of the conventional nine-point scheme and ADM 25-point scheme for r=Δz／Δx=2.5

图5 均匀模型常规9点格式、ADM 25点格式与解析方法单道记录对比Fig.5 Comparison of single traces obtained by conventional nine-point scheme、ADM 25-point scheme and analytical method on homogeneous model

图6 （a）截取的Marmousi速度模型；（b）ADM 25点格式计算的15Hz单频波场；（c）常规9点格式计算得到的时间域地震记录；（d）ADM 9点格式计算得到的时间域地震记录；（e）ADM 25点格式计算得到的时间域地震记录；（f）时间域12阶高阶有限差分方法计算得到的时间域地震记录Fig.6 （a）Truncated Marmousi model；（b）40Hz monochromatic wavefield computed by ADM 25-point scheme；（c）Time-domain seismograms computed with the conventional nine-point scheme；（d）Time-domain seismograms computed with the ADM 9-point scheme；（e）Time-domain seismograms computed with the ADM 25-point scheme；（f）Time-domain seismograms computed with the time domain 12-order high order finite difference scheme

6 结论

频率域常规算法能适用于不同的采样间隔，但是精度较低，而基于旋转坐标系的混合网格算法虽然提高了精度，但是它的局限性在于只适用于相同的方向采样间隔，从而限制了其实际应用的灵活性.而基于平均导数方法的频率域正演方法综合了常规算法和混合网格算法的优点，能在保持混合网格精度的同时适用于不同的方向采样间隔.Chen（2012）的二阶平均导数9点算法能将每个波长所需的网格点数降低到4个网格点数，但是二阶的精度仍然较差.本文将二阶的平均导数频率域正演算法推广到四阶，发展了四阶平均导数频率域正演的算法，构造得到一个优化的四阶精度25点格式，通过系数优化将每个波长所需的网格点数降低到2.78个，相比二阶平均导数格式和四阶常规格式明显提高了计算精度.数值模拟结果表明本文的基于平均导数方法的频率域高阶正演方法不仅具有很好的精度和效率，而且具有很好的适用性和灵活性.

附录A：旋转坐标系二阶空间导数差分离散

下面证明旋转坐标系的二阶空间导数差分离散只适用于等间隔情形，以45°旋转坐标系为例.

45°旋转坐标系二阶空间导数差分离散公式为

对式（A1）右端项的 Pm+1，n+1、Pm-1，n+1、Pm+1，n-1和Pm-1，n-1分别进行泰勒展开：

则有

对式（A2）右端项的Pm，n+1和Pm，n-1再分别进行泰勒展开：

则有

式（A3）式代人式（A2）式得：

即可得到

结合式（A1）得到45°旋转坐标系的二阶空间导数差分离散公式为

其他角度旋转坐标系二阶空间导数差分离散公式推导依此类推.显然上述公式只在Δx=Δz的情况下才成立，因此证明旋转坐标系的二阶空间导数差分离散只适用于等间隔情形.

Alford R M，Kelly K R，Boore D M.1974.Accuracy of finitedifference modeling of the acoustic wave equation.Geophysics，39（6）：834-842，doi：10.1190／1.1440470.

Berenger J P.1994.A perfectly matched layer for the absorption of electromagnetic waves.Journal of Computational Physics，114（2）：185-200，doi：10.1006／jcph.1994.1159.

Cao S H，Chen J B.2012.A 17-point scheme and its numerical implementation for high-accuracy modeling of frequency-domain acoustic equation.Chinese J.Geophys.（in Chinese），55（10）：3440-3449，doi：10.6038／j.issn.0001-5733.2012.10.027.

Chen J B.2012.An average-derivative optimal scheme for frequency-domain scalar wave equation.Geophysics，77（6）：T201-210，doi：10.1190／GEO2011-0389.1.

Clayton R，Enquist B.1977.Absorbing boundary conditions for acoustic and elastic wave equations.Bulletin of the Seismological Society of America，67（6）：1529-1540.

Jo C H，Shin C S，Suh J H.1996.An optimal 9-point，finitedifference，frequency-space，2-D scalar wave extrapolator.Geophysics，61（2）：529-537，doi：10.1190／1.1443979.

Liu L，Liu H，Liu H W.2013a.Optimal 15-point finite difference forward modeling in frequency-space domain.Chinese J.Geophys.（in Chinese），56（2）：644-652，doi：10.6038／cjg20130228.

Liu L，Liu H，Zhang H，et al.2013b.Full waveform inversion based on modified quasi-Newton equation.Chinese J.Geophys.（in Chinese），56（7）：2447-2451，doi：10.6038／cjg20130730.

Lysmer J，Drake L A.1972.A finite-element method for seismology.∥Bolt B A.Methods in computational physics，vol.11：Seismology：Surface waves and earth oscillations.New York：Academic Press，11：181-216.

Marfurt K J.1984.Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations.Geophysics，49（5）：533-549，doi：10.1190／1.1441689.

Operto S，Virieux J，Amestoy P，et al.2007.3Dfinite-difference frequency-domain modeling of visco-acoustic wave propagation using a massively parallel direct solver：A feasibility study.Geophysics，72（5）：SM195-SM211，doi：10.1190／1.2759835.

Pratt R G.1990.Frequency-domain elastic wave modeling by finite differences：A tool for cross-hole seismic imaging.Geophysics，55（5）：626-632，doi：10.1190／1.1442874.

Pratt R G，Worthington M H.1990.Inverse theory applied to multi-source cross-hole tomography，part 1：Acoustic wave equation method.Geophysical Prospecting，38（3）：287-310，doi：10.1111／j.1365-2478.1990.tb01846.x.

Ren H R，Wang H Z，Gong T.2009.Seismic modeling of scalar seismic wave propagation with finite-difference scheme in frequency-space domain.Geophysical Prospecting for Petroleum（in Chinese），48（1）：20-26.

Shin C.1988.Nonlinear elastic wave inversion by blocky parameterization［Ph.D.thesis］.Tulsa，OK：University of Tulsa.

Shin C.1995.Sponge boundary condition for frequency-domain modeling.Geophysics，60（6）：1870-1874，doi：10.1190／1.1443918.

Shin C S，Sohn H J.1998.A frequency-space 2-D scalar wave extrapolator using extended 25-point finite-difference operator.Geophysics，63（1）：289-296，doi：10.1190／1.1444323.

Virieux J，Operto S.2009.An overview of full-waveform inversion in exploration geophysics.Geophysics，74（6）：WCC1-WCC26，doi：10.1190／1.3238367.

Wu G C，Luo C M，Liang K.2007.Frequency-space domain finite difference numerical simulation of elastic wave in TTI media.Journal of Jilin University （Earth Science Edition）.（in Chinese），37（5）：1023-1033.

Yan H Y，Liu Y.2013.Visco-acoustic prestack reverse-time migration based on the time-space domain adaptive high-order finite-difference method.Geophysical Prospecting，61（5）：941-954，doi：10.1111／1365-2478.12046.

附中文参考文献

曹书红，陈景波.2012.声波方程频率域高精度正演的17点格式及数值实现.地球物理学报，55（10）：3440-3449，doi：10.6038／j.issn.0001-5733.2012.10.027.

刘璐，刘洪，刘红伟.2013a.优化15点频率-空间域有限差分正演模拟.地球物理学报，56（2）：644-652，doi：10.6038／cjg20130228.

刘璐，刘洪，张衡等.2013b.基于修正拟牛顿公式的全波形反演.地 球 物 理 学 报，56（7）：2447-2451，doi：10.6038／cjg20130730.

任浩然，王华忠，龚婷.2009.标量地震波频率-空间域有限差分法数值模拟.石油物探，48（1）：20-26.

吴国忱，罗彩明，梁楷.2007.TTI介质弹性波频率-空间域有限差分数值模拟.吉林大学学报（地球科学版），37（5）：1023-1033.