机载探地雷达数值模拟及逆时偏移成像

傅磊，刘四新＊，刘澜波，吴俊军

1吉林大学地球探测科学与技术学院，长春 130026

2康涅狄格大学城市与环境工程系，Storrs 06269

3中国石油集团东方地球物理勘探有限责任公司新兴物探开发处，河北涿州 072751

1 引言

探地雷达（Ground Penetrating Radar）简称GPR，是一种利用电磁波进行无损探测的浅层地球物理技术，被广泛应用于考古学，冰川学，矿产勘查，以及环境与工程等领域.Norhidayahti（2012）等利用探地雷达在马来西亚的仁岭进行考古研究；Arcone（1991）研究了南极洲冰雪覆盖的3.2km深度内的地质结构；Moore等（1999）用50MHz和200MHz雷达天线对挪威斯瓦尔巴特群岛南部的多热型冰川进行了高精度勘察；Singh（2007）利用探地雷达对大型矿砂矿床资源量进行评估.对于植被严重覆盖的区域，或人类无法到达的危险地区如战场、雷场等，常规的探地雷达则显得无能为力，然而机载探地雷达（Damm et al.，2006；刘四新等，2012）（Airborne GPR）却是一种有效的探测手段.

目前，机载探地雷达的发展和其在工程上的应用仍然受很多因素制约.美军寒地研究及工程实验室（CRREL）通过在直升机上悬吊传统探地雷达系统（Arcone，1991），在阿拉斯加及南极洲对冰层厚度及冰层中裂隙进行了探测研究.德国地球科学和自然资源研究所（BGR）开发了一套特殊的机载探地雷达系统（Krellmann et al.，2008），它被安装在AS350直升机上，角反射器天线作为发射和接收天线，操作频率为150MHz，该雷达系统成功应用于地质调查.美国德克萨斯大学奥斯汀分校地球物理研究所（UTIG）开发了固定翼机载探地雷达系统（Holt et al.，2006），该平台包括了重力仪、磁力仪、激光高度计、导航系统、数码相机以及冰雷达，该系统为窄带系统，特点是速度快、功率大.

由于机载探地雷达的天线距离地表较高，其电磁波传播要比常规探地雷达复杂.常规探地雷达天线通过与地面耦合向地下发射电磁波，而机载探地雷达天线首先与空气耦合，电磁波能量在空气中由于几何扩散而衰减，到达地表时，一部分能量反射（散射）回空气中，剩下的能量继续向地下传播，遇到地下介质不连续面便产生反射波，该反射波经过地层衰减以及几何扩散，最终到达接收天线.可见，相比于常规探地雷达，机载探地雷达的探测机理变得更为复杂.

影响机载探地雷达探测效果的因素主要有天线极化方向、天线高度以及地表粗糙度等，为了研究这些因素与机载探地雷达探测效果之间的关系，采用三维时间域有限差分（3D-FDTD）方法对沙漠地区地下空洞掩体机载探地雷达探测进行数值模拟，并分析各因素对探测效果的影响.机载探地雷达探测过程中，起伏的地表会导致地表散射杂波的存在，这些散射杂波的能量一般较强，在地下目标体埋深较浅的情况下，目标体信号会被地表杂波掩盖.为了消除地表杂波的影响，张蓓等（2005）提出子空间地表杂波抑制方法，并取得了一定的效果，本文使用逆时偏移成像（Chang and McMechan，1994；Wu et al.，1996；Sun et al.，2006；龙桂华等，2011；王童奎等，2012；徐兴荣等，2012；孙小东等，2012；王保利等，2012；胡明顺等，2013；张岩和吴国忱，2013）的方法来消除地表杂波的影响.

2 高斯随机粗糙表面

传统探地雷达探测中，与天线接触的地表一般比较平坦，而机载探地雷达探测过程中遇到的地形情况比较复杂.为了模拟粗糙不平的起伏地表，引入高斯随机粗糙表面（Kobayashi et al.，2002；法文哲和金亚秋，2010），它的功率谱表示如下：

其中σ为粗糙表面的均方根高度，它决定了粗糙表面在垂直方向的尺度；kx和ky分别为粗糙面在x和y方向的波数；lx和ly分别为沿x和y方向的相关长度，它与粗糙表面在水平方向的尺度有关.对于一定的水平尺度lx和ly，均方根高度越大意味着表面越粗糙.我们用自由空间中的波数k与均方根高度σ的乘积大小来度量粗糙面的粗糙度.图1所示分别是三种不同粗糙度的高斯随机粗糙表面，本文模拟中，选取水平相关长度lx和ly均为1.25m.图1a是kσ1为0.5的高斯随机粗糙表面，其最大高程为1.14m，最小高程为-0.91m；图1b是kσ2为1的高斯随机粗糙表面，其最大高程为2.28m，最小高程为-1.82m；图1c是kσ3为2的高斯随机粗糙表面，其最大高程为4.56m，最小高程为-3.64m.从图可知，当度量值kσ越大，随机粗糙表面的粗糙度越大.

3 数值模拟及分析

通过对典型地质模型进行雷达波的正演模拟，可以了解电磁波在介质中的传播过程，有助于对雷达数据的解释.从麦克斯韦微分方程组出发，Yee（1966）提出了时间域有限差分求解法，它将麦克斯韦旋度方程组进行差分离散，在时间上迭代推进求解空间中每一个时刻的电磁场值.

本文利用三维时间域有限差分法（刘四新等，2005；2007；2011；2012；Taflove et al.，2005）对起伏的沙漠地区地下空洞掩体机载探地雷达探测进行了数值模拟.图2a是建立的三维地质模型，其空间尺度在x方向为116m，在y方向为60m，在z方向为30m.用度量值kσ2=1高斯随机粗糙表面代表起伏的沙漠表面，沙漠表面所在的平均高程为15m，即干沙的厚度约为15m，其相对节电常数为4，电导率为0.1mS·m-1.在干沙地层内部有两个沿y走向空洞掩体，分别用充满空气的两个圆柱体表示.图2b是y=15m处的二维切片模型，从图可知，两个空洞的xz截面中心坐标分别为（48，10.5）和（68，7.5）m，空洞的截面半径均为1.5m.图中虚线代表天线的飞行轨迹，即合成数据的记录位置，其距离平均地表的平均高度约12m，水平方向30～90m，每隔0.5m记录一道数据.

图2 （a）沙漠地区空洞三维模型；（b）相应的二维模型，色标为相对介电常数，无量纲Fig.2 （a）Three-dimensional model of cavity embedded in the sand；（b）Corresponding two-dimensional model

3.1 波场快照分析

整个模型空间离散为0.2m的立方体单元格，选取中心频率为50MHz的雷克子波作为激励源，时间采样间隔为0.2ns，时窗为250ns.当激励源位于合成记录位置的中点，采用x方向的电场极化，截取不同时刻的波场快照，见图3，白色星号表示激励源所在位置，白色曲线代表起伏的沙漠地表，两个圆形分别代表地下目标体.观察y=15m截面不同时刻x方向的电场，图3a是60ns时刻的波场快照，可以看到此时波前刚刚传到起伏的沙漠表面，在高程大于平均高程（15m）的60m处，已经有部分能量散射到空气中；图3b是100ns时刻的波场快照，从图可知，由于起伏地表的影响，一部分能量散射回空气中，并且散射波杂乱交错，剩下的能量穿透沙漠地表继续往前传播，其波前面已经触及到浅部异常体，并且波前面变的不规整；图3c是140ns时刻的波场快照，此时波前面已经传到深部异常体，发现两个异常体的反射波能量弱于空气中的散射杂波能量；图3d是180ns时刻的波场快照，其波前面可以看做是在起伏地表上的许多二次源的波前面叠加效果，可见起伏地表会造成地表散射杂波，而且其能量往往强于地下目标体反射回波信号.

3.2 不同天线极化方向对探测效果影响分析

机载雷达探测实际过程中，由于直升机的飞行速度、当地风向及风速的变化等影响，天线的姿态会发生变化，如左右旋转，上下摇摆.根据机载雷达的特殊性，本文研究了四种典型的天线配置方式，如图4所示，天线的飞行轨迹为沿x方向的带右端箭头的虚线，其中FBy代表天线平行并分别配置于直升机的头部和尾部，天线的极化方向为y方向；FBx代表天线同轴共线配置于直升机的头部和尾部，天线的极化方向为x方向；LRy代表天线共线配置于直升机的左右两翼，天线的极化方向为y方向；LRx代表天线平行配置于直升机的左右两翼，天线的极化方向为x方向.

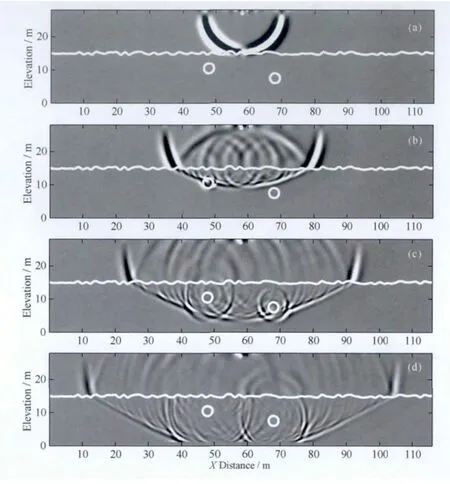
图3 不同时刻的波场快照Fig.3 Wave field snapshots at different time

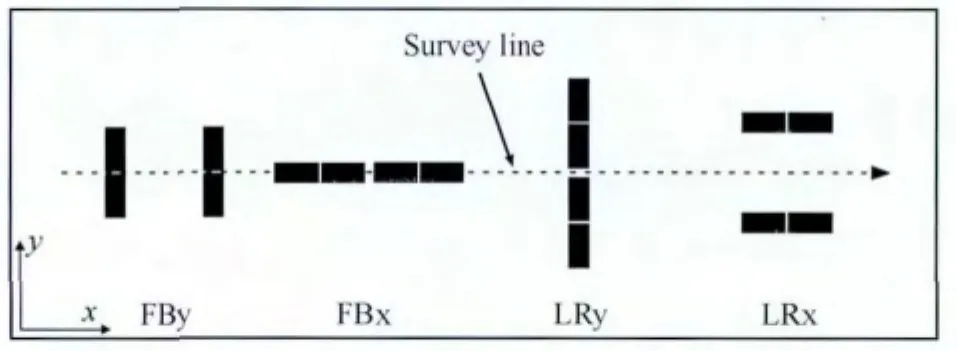
图4 机载探地雷达四种不同的天线配置方式Fig.4 Four different antenna configurations for airborne GPR survey

根据四种典型的天线配置方式，研究了不同极化方式对机载探地雷达探测地下异常体的影响.选取粗糙度为kσ2=1的高斯随机表面代表起伏的沙漠表面，固定天线距离沙漠地表高度为12m，模型参数与图2所示三维模型保持一致.图5是四种典型的天线配置情况下获得的机载探地雷达探测地下空洞掩体的雷达剖面，图中的直达波均已去除.图5a是天线分别配置于直升机头部和尾部，y方向极化时获得的模拟雷达剖面，从图可知，地表的散射杂波主要集中在110～130ns，其能量远远强于地下目标体能量，浅部异常体反射信号完全淹没于杂波中，但是来自深部异常体的双曲形态反射信号仍然能被识别；图5b是天线同轴共线分别位于直升机头部和尾部，x方向极化时获得的模拟雷达剖面，从中可知，地表的散射杂波能量仍然比较强，但是浅部的异常体目标反射信号以及深部的目标反射信号均可以被识别；图5c是天线分别位于直升机左右两侧，x方向极化时获得的模拟雷达剖面，强地表杂波淹没了浅部目标体信号；图5d是天线分别位于直升机左右两侧，y方向极化时获得的模拟雷达剖面，图中来自地表的散射杂波能量主要集中在110～130ns范围内，浅部目标体仍然可以识别.

综上可知，当天线的极化方向与异常体的走向平行时，地下浅部目标体的信号被来自地表的强杂波覆盖，地下浅部异常体目标很难被识别，而当天线的极化方向与异常体垂直时，地下异常体目标反射波能量增强，虽然地表杂波能量较强，但是浅部异常体目标仍然可以被识别.因此，在机载探地雷达实际探测过程中，在保证测线与异常体走向垂直的同时，天线飞行过程中应尽量保证天线的极化方向与异常体走向垂直.

3.3 天线高度对探测效果影响分析

图5 四种不同天线配置方式下模拟的雷达剖面Fig.5 Simulated profile results for four antenna configurations of Airborne GPR

机载探地雷达探测过程中，为了保证天线的飞行姿态稳定，天线的飞行轨迹应避开地表植被以及地面建筑物，即天线距离地面高度不能过低.为了研究天线距离地表高度对探测结果的影响，选取粗糙度为kσ2=1的高斯随机粗糙表面代表起伏的沙漠表面，天线位于直升机左右两侧，激励源的极化方向为x方向极化，模型中的其他参数保持不变，改变天线的高度，分别从6m到8m、10m、12m（如图6所示）模拟了不同高度情况下沙漠地区地下空洞掩体机载雷达探测雷达剖面，图中直达波均已去除.图6a是当天线距离地表平均高度为6m时得到的合成雷达剖面，从图可知，位于浅部的异常体及深部的异常体反射波双曲形态同向轴清晰可见，来自地表的散射杂波能量较强，图6b是天线距离地表平均高度为8m时的合成雷达剖面，图6c是天线距离地表平均高度为10m时的合成雷达剖面，图6d是当天线距离地表平均高度为12m时获得的雷达剖面，从图可知，随着天线距离地表的距离增加，来自地下异常体的反射波的能量越来越弱，其双曲线型同向轴的振幅变小，同向轴越来越模糊，而来自地表的反射杂波的能量仍然很强.对于机载探地雷达探测地下异常体，发射天线发射的电磁波能量在空气中由于几何扩散而衰减，其能量与距离的二次方成反比，随着天线高度增加，到达地表的能量减少，从而降低了信噪比，不利于地下异常体的探测.机载雷达野外实际探测中，为了得到更高分辨率的雷达图像，在保证天线飞行姿态稳定的情况下，天线高度尽可能降低.

3.4 粗糙表面对探测效果影响分析

传统探地雷达探测过程中，天线与地面耦合，大部分能量直接向地下传播；而机载探地雷达探测过程中，天线位于距离地面较高的空中，发射天线发出的电磁波在空气中由于几何扩撒而损耗能量，当电磁波到达地表时，粗糙不平的地表会导致电磁波的空间各个不同方向的散射，为了研究不同粗糙度表面对探测结果的影响，把天线距离地面的高度固定为12m，天线位于直升机左右两侧，激励源为x方向极化，其他模型参数保持不变，改变沙漠地表的粗糙度.图7是沙漠地表不同粗糙度情况下获得的机载探地雷达探测地下空洞的模拟结果.图中水平方向是沿x方向的距离，垂直方向是电磁波双程传播时间，图中所有剖面的直达波都已去除.

图6 不同天线高度下模拟的雷达剖面Fig.6 Simulated radar profile of different antenna height

图7a是沙漠地表水平情况下得到的雷达剖面，从图可知，水平同向轴是来自沙漠地表的反射波，而两条双曲线分别代表来自地下空洞的反射波，两条双曲线的顶点位置反映了异常体所在的水平位置，从剖面可知，第一个异常体水平位置为48m，第二个异常体的水平位置为68m，这与模型是一致的.图7b是沙漠表面粗糙度为kσ1=0.5时的雷达剖面，相比于图7a，可以发现，虽然来自沙漠表面以及地下空洞的反射波均能清晰地识别，但是雷达剖面在110～130ns之间出现了很多地表散射杂波，这些杂波的存在势必给剖面的解释带来困惑，另外来自地下空洞的反射波的振幅稍有变小.图7c是沙漠表面粗糙度为kσ2=1时的雷达剖面，仍然可以清晰地识别来自沙漠表面的反射波，然而由于沙漠表面粗糙度的增加，导致电磁波在地面的散射更严重，穿透到地下的电磁波能量更少，所以来自地下空洞的反射同向轴变得模糊，位于110～130ns的散射波能量变的更强.图7d是沙漠表面粗糙度为kσ3=2的雷达剖面，来自地表的散射杂波能量进一步增强，而来自地下异常体的反射波的双曲线形态已经很难被识别.从该剖面中，我们很难定位地下异常体的位置.

由此可见，粗糙的地表会导致电磁波的散射，地表散射而损耗的电磁波能量越多，散射杂波的能量越强，同时，穿透到地下的电磁波能量相应的就越少，来自地下目标体的反射波能量就越弱.反映在雷达剖面中图像分辨率降低，不利于机载探地雷达探测的开展.

4 逆时偏移成像

雷达电磁波与地震波在运动学上存在相似性，反射地震上的偏移技术可以借鉴到探地雷达数据处理中.偏移的目的是为了使雷达剖面中倾斜界面共深度映像聚焦，使绕射波归位.为了消除机载探地雷达探测中由于起伏地形产生的地表散射杂波影响，借鉴反射地震中的逆时偏移成像（RTM）技术.

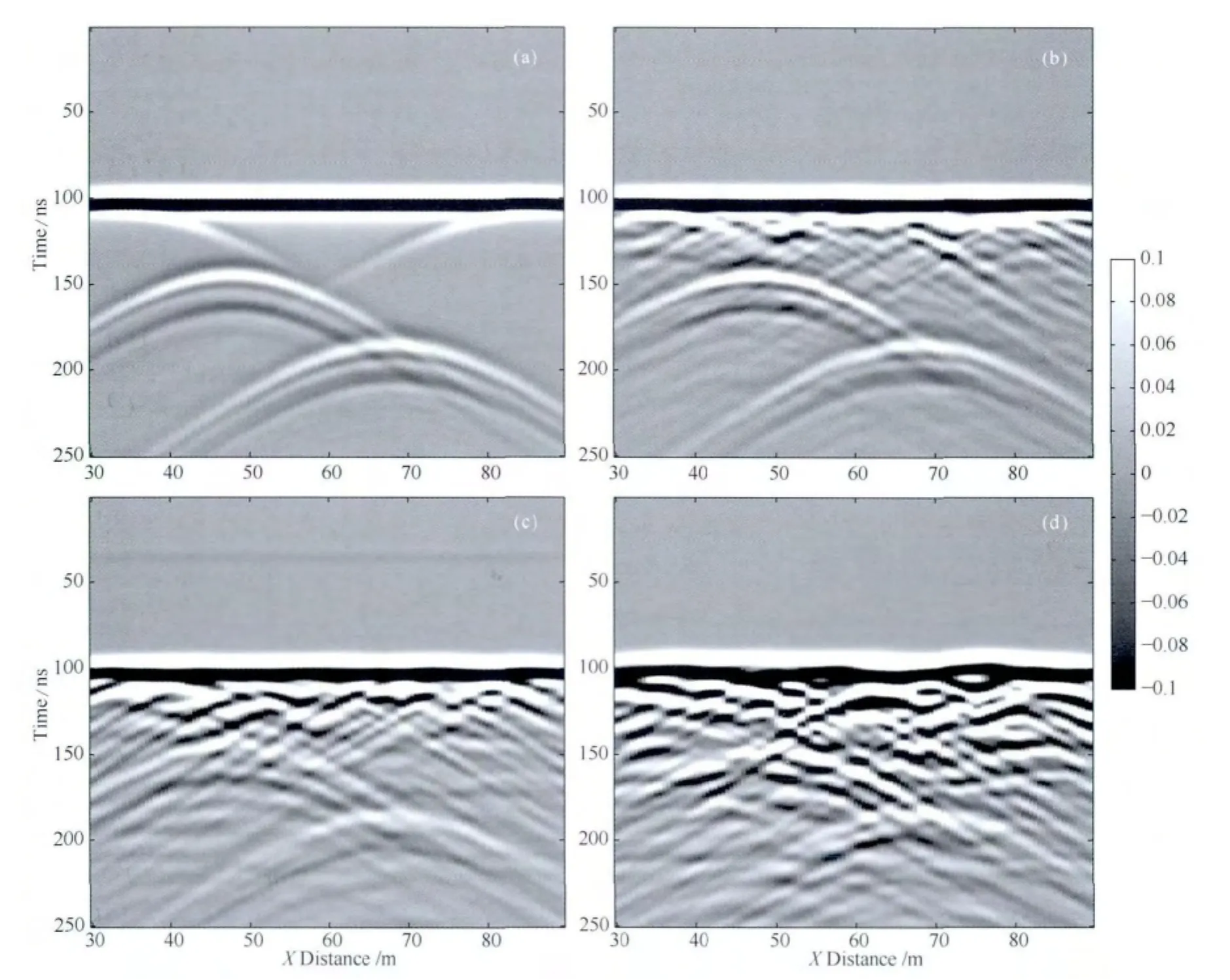
图7 机载探地雷达于沙漠地区探测地下空洞的模拟结果Fig.7 Radar profile of airborne GPR detecting cavities at desert area

地震上逆时偏移可分为叠前逆时偏移和叠后逆时偏移.叠前偏移是把共炮点道集记录或共偏移距道集记录中的反射波归位到产生它们的反射界面上并使绕射波收敛到产生它的绕射点上，最后得到能够反映界面反射系数特点的并正确归位了的地震波形剖面.叠后偏移是在水平叠加剖面的基础上进行的，针对水平叠加剖面上存在的倾斜反射层不能正确地归位和绕射波不能完全收敛的问题，采用了爆炸反射面的概念来实现倾斜反射层的正确归位和绕射波的完全收敛.相对其他方法而言，逆时偏移用全程波方程对波场延拓，避免对波动方程的近似，因此没有倾角限制，原理上可以利用转换波、棱镜波、或者多次反射波成像，并获得更精确的振幅等动力学信息，实现保幅成像，还可以更好地对复杂速度成像进行更细化更精确的估计，成像方法不受介质速度变化的影响，能够对复杂区域进行较准确的成像.

本文借鉴反射地震叠前偏移技术，采用和勘探地震中类似的共炮集观测方式合成雷达数据.为了合成共炮集数据，采用1个发射天线及8个接收天线，接收天线间距为1m，发射天线与第一个接收天线的偏移距为3m，发射天线每次移动距离为1m，这样可以获得一个共炮集数据集.合成数据时，天线距离地面的高度固定为12m，激励源为x方向极化，其他模型参数保持不变，改变沙漠地表的粗糙度，获得不同粗糙度情况下共炮集雷达数据集.

图8 不同地表粗糙度情况下雷达剖面偏移成像结果Fig.8 GPR migration results for different roughness surface

采用二维RTM算法，对共炮集雷达数据集进行逆时偏移成像，同时为了对比说明RTM的成像效果，本文给出了基尔霍夫偏移成像（Duquet et al.，2000；Eaton et al.，2002；Zhu and Lines，1998）结果，如图8所示.图中左边一栏四个图是来自基尔霍夫偏移成像的结果，右边一栏是来自二维逆时偏移成像的结果.图8a是水平地表情况下基尔霍夫偏移成像结果，其地下目标体的反射波聚焦较好，聚焦位置基本反映了地下目标体的空间位置，图8e是地表情况下逆时偏移成像结果，从中可知，地下目标体的空间位置、几何形态及尺寸与实际模型基本一致；图8b是在kσ1=0.5的粗糙表面情况下获得的基尔霍夫偏移成像结果，图中散射杂波仍然杂乱无章，散射杂波并没有得到聚焦，杂波的存在仍然会影响地下异常体的判断，图8f是对应的逆时偏移结果，来自地表的散射杂波归位，地下目标体清晰可见，地下目标体的空间位置、几何形态、尺寸以及起伏地表与实际模型基本一致；同样的，图8g和图8f中的偏移成像结果明显好于图8c和图8d的.

基尔霍夫偏移技术只能让地下反射目标体信号聚焦，聚焦位置大致反映目标体空间位置，无法聚焦的散射杂波仍然会对数据解释造成困扰，随着地表粗糙度增加，地下目标体聚焦能量减弱，而逆时偏移成像技术不但可以使地下目标体反射波聚焦，刻画地下目标体空间位置、几何形态及尺寸大小，而且可以让地表散射杂波归位，同时起伏的地形亦得到刻画.

5 结论

（1）数值模拟试验表明天线的极化方向与异常体走向垂直时更利于探测地下目标体，因此机载雷达野外探测时，为了得到更高分辨率的雷达图像，测线与异常体走向垂直的同时，尽可能地保证天线的极化方向与异常体走向垂直.

（2）随着天线高度的增加，从发射天线发射出的电磁波能量由于几何扩散而衰减更多，不利于探测，实际野外探测中，保证天线姿态稳定的情况下，飞行高度尽可能地降低.

（3）地表粗糙度的增加会导致地表散射杂波增强，造成传播到地下的电磁波能量减少，削弱地下目标体信号，雷达剖面的分辨率降低，不利于地下异常体目标识别.

（4）成功借鉴反射地震上逆时偏移成像技术，使地下目标体反射波聚焦，聚焦位置很好地刻画了异常体的空间位置、几何形态及尺寸大小，同时，可以使地表散射杂波归位，起伏的地形在偏移后的剖面中得到刻画；随着地表粗糙度的增加，基尔霍夫偏移成像结果更差，而逆时偏移成像结果仍然能够很好地刻画起伏地形及异常体.

Arcone S A.1991.Dielectric constant and layer-thickness interpretation of helicopter-borne short-pulse radar waveforms reflected from wet and dry river-ice sheets.IEEE Transactions on Geoscience and Remote Sensing，29（5）：768-777.

Arcone S A.1996.High resolution of glacial ice stratigraphy；A ground-penetrating radar study of Pegasus Runway，McMurdo Station，Antarctica.Geophysics，61（6）：1653-1663.

Chang W F，McMechan G A.1994.3-D elastic prestack，reversetime depth migration.Geophysics，59（4）：597-609.

Damm V，Casassa G，Blindow N，et al.2006.Airborne GPR measurements in the Atacama Desert first results and constraints using a 150MHz pulse radar for groundwater exploration.11th International Conference on Ground Penetrating Radar，19-22.

Docherty P.1991.A brief comparison of some Kirchhoff Integral formulas for migration and inversion.Geophysics，56（8）：1164-1169.

Duquet B，Marfurt K J，Dellinger J A.2000.Kirchhoff modeling，inversion for reflectivity，and subsurface illumination.Geophysics，65（4）：1195-1209.

Eaton D W，Hope J，Bohlen T.2002.An elastic Kirchhoff method for computing synthetic seismograms：Modeling the receiverfunction response of an irregular Moho surface.Seismol.Res.Lett.，73（2）：232.

Fa W Z，Jin Y Q.2010.Simulation of radar sounder echo from lunar surface structure.Sci.China Earth Sci.，40（4）：473-485.

Holt J W，Peters M E，Morse D L，et al.2006.Identifying and characterizing subsurface echoes in airborne radar sounding data from a high-clutter environment in Taylor Valley，Antarctica.∥Proc.the 11th Int.Conf.on Ground Penetrating Radar，AIR.3-5.

Hu M S，Pan D M，Dong S H，et al.2013.Optimization for random boundary building in reverse-time migration based on scattering theory.Progress in Geophys.（in Chinese），28（4）：2069-2077.

Kobayashi T，Oya H，Ono T.2002.A-scope analysis subsurface radar sounding of lunar mare region.Earth，Planets and Space，54（10）：973-982.

Krellmann Y，Lentz H，Triltzsch G.2008.Stepped-frequency radar system in gating mode：An Experiment as a new helicopterborne GPR system for geological applications.IEEE Geosci.and Remote Sens.Symp.1：153-156.

Liu S X，Sato M.2005.Transient radiation from an unloaded，finite dipole antenna in a borehole：experimental and numerical results.Geophysics，70（6）：k43-k51.

Liu S X，Zeng Z F，Xu B.2006.FDTD simulation of ground penetrating radar signal in 3-dimensional dispersive medium.Journal of Jilin University （Earth Science Edition），36（1）：123-127.

Liu S X，Feng Y Q，Fu L，et al.2012.Advances and numerical simulation of airborne ground penetrating radar.Progress in Geophys.（in Chinese），27（2），0727-0735.

Long G H，Zhao Y B，Li X F，et al.2011.Accelerating 3D staggered-grid finite-difference seismic wave modeling on GPU cluster.Progress in Geophys.（in Chinese），26（6）：1938-1949.

Liu S X，Zeng Z F，Deng L.2007.FDTD simulations for ground penetrating radar in urban applications.Journal of Geophysics and Engineering，4（3）：262-267.

Liu S X，Wu J J，Zhou J F，et al.2011.Numerical simulations of borehole radar detection for metal ore.IEEE Geosci.and Remote Sens.Lett.，8（2）：308-312.

Liu S X，Wu J J，Dong H，et al.2012.The experimental results and analysis of a borehole radar prototype.Journal of Geophysics and Engineering，9（2）：201.

Moore J C，Pälli A，Ludwig F，et al.1999.High-resolution hydrothermal structure of Hansbreen，Spitsbergen，mapped by ground-penetrating radar.Journal of Glaciology，45（151）：524-532.

Muztaza N M，Saidin M M，Azwin I N，et al.2012.Archaeological structure detection using 3DGPR survey in Jeniang，Kedah，Malaysia.∥International Proceedings of Chemical，Biological and Environmental Sciences，36：49-53.

Singh N K.2007.Ground penetrating radar（GPR）mineral base profiling and orebody optimization.∥The 6th International Heavy Minerals Conference.Hluhluwe，South Africa，185-194.

Sun R，McMechan G A，Lee C S，et al.2006.Prestack scalar reverse-time depth migration of 3Delastic seismic data.Geophysics，71（5）：S199-S207.

Sun X D，Li Z C，Wang X L.2012.Pre-stack reverse-time migration using a finite difference method based on triangular grids.Progress in Geophys.（in Chinese），27（5）：2077-2083.

Taflove A，Hagness S.2005.Computational Electrodynamics：The Finite-Difference Time-Domain Method （3rd ed）.London：Artech House.

Wang B L，Gao J H，Chen W C，et al.2012.Efficient boundary storage strategies for seismic reverse time migration.Chinese J.Geophys.（in Chinese），55（7）：2412-2421.

Wang T K，Li Y，Guo A H，et al.2012.The study of reverse-time migration technology in Nanpu 1st structure.Progress in Geophys.（in Chinese），27（6）：2541-2547.

Xu X R，Wang X W，Wang Y C，et al.2012.Study and application of imaging condition for reverse-time migration based on wavefields separation.Progress in Geophys.（in Chinese），27（5）：2084-2090.

Wu W J，Lines L R，Lu H X.1996.Analysis of higher-order，finite-difference schemes in 3-D reverse-time migration.Geophysics，61（3）：845-856.

Yee K.1966.Numerical solution of initial boundary value problems involving Maxwell′s equations in isotropic media.IEEE Transactions on Antennas and Propagation，14（3）：302-307.

Zhang Y，Wu G C.2013.Review of prestack reverse-time migration in TTI media.Progress in Geophys.（in Chinese），28（1）：0409-0420.

Zhang B，Liu J X，Wu R B.2005.Research on subspace-based GPR ground bounce removal method.Signal Processing，21（4）：514-517.

Zhu J M，Lines L R.1998.Comparison of Kirchhoff and reversetime migration methods with applications to prestack depth imaging of complex structures.Geophysics，63（4）：1166-1176.

附中文参考文献

法文哲，金亚秋.2010.雷达探测仪对月球次表层结构的探测模拟方法.中国科学：地球科学，40（4）：473-485.

胡明顺，潘冬明，董守华等.2013.基于散射理论的逆时偏移随机边界构建策略优化分析.地球物理学进展，28（4）：2069-2077.

刘四新，曾昭发，徐波.2006.三维频散介质中地质雷达信号的FDTD数值模拟.吉林大学学报（地球科学版），36（1）：123-127.

刘四新，冯彦谦，傅磊等.2012.机载探地雷达的进展以及数值模拟.地球物理学进展，27（2）：727-735.

龙桂华，赵宇波，李小凡等.2011.三维交错网格有限差分地震波模拟的GPU集群实现.地球物理学进展，26（6）：1938-1949.

孙小东，李振春，王小六.2012.三角网格有限差分法叠前逆时偏移方法研究.地球物理学进展，27（5）：277-2083.

王保利，高静怀，陈文超等.2012.地震叠前逆时偏移的有效边界存储策略.地球物理学报，55（7）：2412-2421.

王童奎，李莹，郭爱华.2012.逆时偏移技术在南堡1号构造中的应用研究.地球物理学进展，27（6）：2541-2547.

徐兴荣，王西文，王宇超等.2012.基于波场分离理论的逆时偏移成像条件研究及应用.地球物理学进展，27（5）：2084-2090.

张岩，吴国忱.2013.TTI介质叠前逆时偏移成像研究综述.地球物理学进展，28（1）：409-420.

张蓓，刘家学，吴仁彪.2005.探地雷达子空间地杂波抑制方法研究.信号处理，21（Z1）：514-517.