从重力场识别与提取地壳变形带信息的方法研究

孙艳云，杨文采

1中国地质大学地球物理与信息技术学院，北京 100083

2中国地质科学院地质研究所 “大地构造与动力学”国家重点实验室，北京 100037

1 引言

大陆构造单元边界通常都是不同地质时期的地壳变形带.如果能够用数学方法把地壳变形带信息从地球物理场中识别和提取出来，用计算机自动识别大陆构造单元就成为可能.迄今为止，大陆构造单元的划分都是大地构造学家各自进行的，不同大地构造学家划分的大陆构造单元各自不同，缺乏客观的标准.我们希望应用现代数学方法把地壳变形带信息从地球物理场中识别和提取出来，用人工智能让计算机自动识别大陆构造单元，为大地构造学家提供一个有准确定位的岩石圈构造单元的客观模型.为此目的，以区域重力场作为信息识别和提取的首选，其原因不仅是因为区域重力资料容易采集，而且作为重力异常源的密度参数乃是反映物质属性的最重要参数.我们期望这一项研究能够为人工智能应用于地球物理解释提供一个成功的先例.

近20年来，重力勘探仪器与采集方法的不断进步，观察精度及采集的信息量明显提高，促进了位场资料处理方法技术的迅速发展（刘天佑，2007）.目前，位场资料的处理方法众多，主要归纳为两类，其一，传统的位场资料处理方法，如延拓、导数及其优化组合、各种滤波等（Dean，1958；Guspíand Introcaso，2000；Boschetti et al.，2004）；其二，基于近代数学的位场资料处理方法，如神经网络、小波变换、曲波变换等（Raiche，1991；杨文采，1997；侯遵泽和杨文采，1997；杨文采等，2001；陈玉东，2003；陈召曦，2012）.这些方法都可对场进行分离，对提取场源边界、埋深、走向及倾向等信息有一定帮助.其中，在位场图上表现为线状的异常带或梯度带常在平面上与构造单元边界吻合.对此，国内外已经进行了大量的研究并发展了多种方法技术，如水平总梯度法、斜导数法、斜导数的总水平梯度法等（Cordell，1979；Miller and Singh，1994；Cooper and Cowan，2006；Cooper and Cowan，2008；王彦国等，2013）.但是，不同类型的地壳变形的强度可能相差很大，不同时期的地壳变形保留在地壳岩石中的密度变化也相差悬殊，因此单纯用线状重力异常的幅度或者重力梯度幅度大小并不能完整准确地识别和圈定地壳变形带.必须研究新的数学方法对地壳变形带进行更有效的提取.

从物理学的观点看，地壳变形带是动力地质作用在地壳中的刻痕，它造成地壳岩石的密度在局部呈带状变化.因此，不同强度的地壳变形带是岩石圈地质作用在地壳中的刻痕，对应地壳中长条形密度异常带，它们又在重力场中造成“刻痕”.这种刻痕的特征参数包括：重力异常梯度急剧变化，异常在平面上各向异性较强，各向异性长轴走向比较稳定等.把隐含在重、磁异常中有关刻痕的所有特征参数都提取出来，可在综合分析的基础上识别不同时期形成的地壳变形带，为大陆构造单元划分提供可靠依据.目前已有的位场资料数据处理技术尚无提取位场异常内隐含刻痕信息的方法，本文介绍的就是我们对区域重力场刻痕信息识别的初步研究成果.

表面形貌识别指用具体的参数表征表面各区段的几何形态及属性，并最终对不同类型的表面形貌进行识别，表面刻痕识别是其中的一种.以随机过程理论为基础的表面刻痕识别技术可以确切地识别表面形貌的各项特征（Longuet-Higgins，1962；黄逸云，1984；黄逸云，1985；Thomas，1987），其二阶谱矩及统计不变量可以对表面的刻痕深度以及各向异性进行详细地刻画，因而1970年代后开始发展并用于工业界（Nayak，1973；Li et al.，2000；Yanagi et al.，2001；杨叔子等，2007）.有关刻痕的特征参数中，重力异常幅度变化只反映刻痕的深度，而不反映刻痕的存在与否，而异常在平面上的各向异性更依赖于刻痕的存在.表面刻痕识别分析和识别之所以会优于以往重、磁异常处理方法，其基础正是强调了各向异性参数的准确计算.因此，若将表面刻痕识别的数学原理用在区域重力场刻痕智能提取上，则可以进行地壳变形带更有效的识别.

本文介绍以随机过程理论为基础的表面刻痕识别的原理和地壳变形带信息识别方法，并通过对理论模型数据及桐柏—大别试验区区域布格重力异常数据的刻痕识别，深入探讨区域布格重力场上利用表面刻痕识别对地壳变形带提取的方法技术.试验表明，这种方法对识别地壳变形带和区域构造单元划分是有效的.

2 区域位场刻痕信息识别的原理

区域位场函数g=g（x，y）是一个二维连续可微函数，可视为表面函数z=f（x，y）的一种特殊类型，其中表面刻痕属于表面形态的一种特殊类型（Longuet-Higgins，1962；Thomas，1987；杨叔子等，2007）.表面形态的信息提取从表面谱矩计算入手.

2.1 位场表面谱矩

一个表面可用函数z=f（x，y）定义，表面形态的局部性状要用表面谱矩函数表征.因此，讨论刻痕识别之基础在于表面谱矩的计算，现讨论如下.

在x、y、z组成的笛卡尔直角坐标系中，位场表面用两维函数z（x，y）来表征.其中，（x，y）为平面直角坐标位置，z表示位场函数.作为表面的二维函数z（x，y）的二维快速傅里叶变换（Thomas，1987）为

式中fx和fy别代表x和y两个相互垂直方向上的波数.

位场表面的二维功率谱密度可以用傅里叶变换的形式表示为

式中F＊（fx，fy）表示傅里叶变换的共轭函数.

由随机过程理论可知，2个随机变量x和y的p+q阶矩mpq（Longuet-Higgins，1962；Thomas，1987）为

式中X、Y分别为变量x、y的随机过程函数.

对于连续的位场表面的形貌分析，相应的表面功率谱密度的p+q谱矩阶（Longuet-Higgins，1962；Thomas，1987；Yanagi et al.，2001）为

由于实际测量中位场表面的面积以及采样点数均有限，假定在x方向以间隔Δx等间距采样，在y方向上以间隔Δy等间距采样，且采样点数分别为M和N，则位场表面二维离散傅里叶变换式为

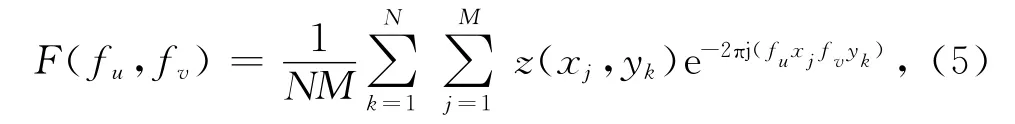
式中fu，fv是离散空间频率（即波数）

如下推导可得位场表面对应的离散二阶谱矩空间域表达式为

其中

令p=2，q=0，函数F（fu，fv）的逆离散傅里叶变换为

则表面二阶谱矩的三个元可以用褶积形式表示为

同理可证

其中

表面二阶谱矩的三个元都有其各自的物理含义.m20、m02分别表示位场表面X和Y方向的斜率的方差；m11是X和Y方向的斜率的协方差.位场轮廓是指一个切平面（即截平面）与位场表面的交线.若已知表面的二阶谱矩为m20、m02、m11，位场表面任意一条轮廓在θ（与x轴方向的夹角）方向上的二阶谱矩m2（θ）由下式唯一确定（Thomas，1987；杨叔子等，2007）为

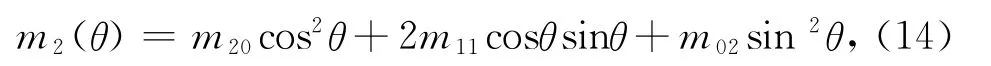
m2（θ）等于θ方向上轮廓的斜率的方差.若m2max和m2min是m2（θ）的最大值和最小值，则其所在的方向总是相互垂直的，这两个方向称为刻痕主方向，m2min的那条轮廓曲线与x轴的夹角称为主方向角θp，场源边界处对应的主方向角表示其走向，即

2.2 位场表面统计不变量与脊形化系数

位场表面谱矩依赖于坐标系，如果坐标系旋转，尽管此时表面性质不变，表面的谱矩将也会改变.因此，需要考虑一种与坐标系旋转无关的统计不变量.位场表面的二阶谱矩可以用统计不变量M2和Δ2来表达（Huang，1984；Huang，1985；Thomas，1987）为

统计不变量M2表示位场表面的二维斜率的方差，可以表征布格重力异常的刻痕强弱，定义为刻痕的强度系数；试验表明，M2着重表现幅度大的表面形貌.统计不变量Δ2主要与场在局部区域的各向异性有关，表示表面刻痕脊形化的程度，且总有Δ2≥0.试验表明，脊形化反映的是场在局部区段各向异性的程度，Δ2可以较全面地反映表面形态随方向变化的形貌.

为了对位场表面的刻痕准确定位，我们希望同时使用两个二阶谱矩的统计不变量M2和Δ2来描述所有可能的位场刻痕.将这种综合参数定义为刻痕的脊形化系数Λ，定义为

在提取构造单元边界信息时，边界越窄单元划分的定位越准确.为了准确地对边界定位，还可对与边界相关的刻痕强度系数进一步作增强处理.定义MΛ为边界脊形化系数）其中MΛa和MΛb为边界脊形化系数分量，计算公式为Δ

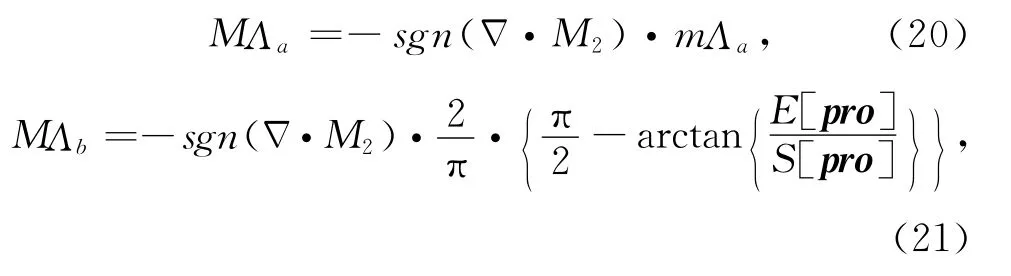
式中，矩阵pro为

函数E［pro］为矩阵pro的均值，S［pro］为矩阵pro的标准方差，mΛa为以M2为初始表面提取的脊形化系数，其它参数为

且记

以上就是区域位场函数刻痕信息提取计算的理论，区域位场函数刻痕信息就是按公式（18）—（19）计算刻痕的脊形化系数Λ和边界脊形化系数MΛ.

3 理论模型数据试验

不同强度的地壳变形带是岩石圈地质作用在地壳中的刻痕，对应地壳中长条形密度异常带，可用长条形密度异常带模拟.为检验上述方法的正确性，采用图1的地壳模型进行理论试验.图1a为两个不同大小、走向及埋深的长条形密度异常带，模拟两个不同大小、走向及埋深的地壳变形带.较浅长条形密度异常带A走向为西偏南30°，长和宽分别为170km和10km，顶面埋深为5km，中心坐标为（-24.5km，42.5km，7.5km），其剩余密度值为0.8g·cm-3；较深长条形密度异常带B走向为东西方向，长和宽分别为190km和10km，顶面埋深为10km，中心坐标为（-3.15km，-5km，12.5km），其剩余密度值为0.3g·cm-3；x轴与y轴方向点距均为0.1km.图1b为由地壳变形带模型正演计算出的理论重力异常，图1c为水平总梯度异常，极大值出现在两组地壳变形带交汇处，虽然能反映变形带边界但幅度变化大，宽度较粗，定位不够准确.

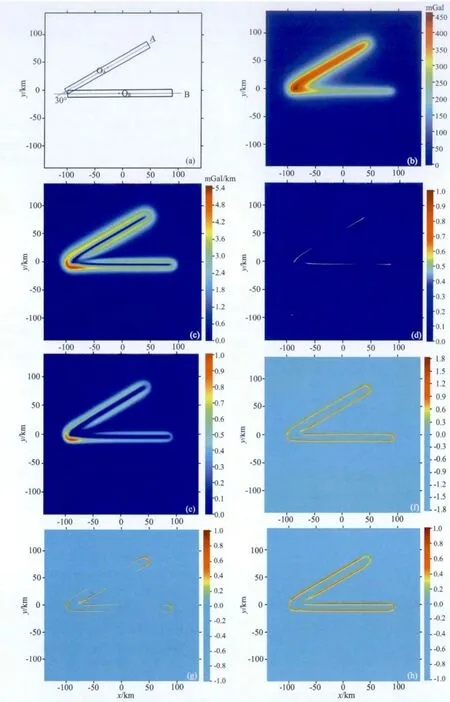
图1 地壳变形带模型、理论重力异常、水平总梯度异常以及地壳变形带信息识别方法提取结果Fig.1 Model of crustal deformation beltssynthetic data settotal horizontal derivative of the synthetic data set and results from the information recognition of crustal deformation belts

采用本文方法以0.9km滑动窗口半径对理论重力异常图1b进行信息提取，提取结果见图1d～h.理论重力异常表面刻痕的脊形化系数Λ示如图1d.由图可见，两变形带的刻痕的脊形化系数Λ在其中心线上异常明显，呈线状分布，反映了变形带的存在.变形带相交处的领域脊形化系数Λ值很大，反映出该处变形程度强，并且变形方向不唯一.另外，该表面上两条变形带之间还夹着一从西南至东北方向逐渐减小的低Λ值条带，呈帚状展布，为呈锐角的两变形带对所夹单元各向异性的影响，并不存在真实的变形带.经试验发现这种影响随着夹角的减小而增大.图1e为刻痕的强度系数M2，梯度越大其值越高，表示此处边界越强.与水平总梯度（图1c）结果相比，刻痕的强度系数M2由于采用较小半径的滑动窗口导致变形带边界位置的梯级带宽度稍窄，但两者主要反映较强的边界刻痕且梯级带宽度均较大，不利于弱变形带的识别.图1f显示边界脊形化系数MΛ，较大的值指示变形带边界的位置.图中可见，边界刻痕宽度紧缩，并且对边界走向方向的梯度变化敏感，因而可更准确地刻画出大陆地壳中不同构造单元的边界，因为不同构造单元的边界往往是脊形化系数大的地壳变形带.图1g与图1h分别为边界脊形化系数分量MΛa与MΛb，二者是一对可以对边界进行详细刻画且互补的参数，若定义在其走向上梯度变化很小的边界为平直边界，反之为扭曲边界，则较大的MΛa值表示变形带的边界可能扭曲或发生汇聚，而强MΛb值则对应变形带中的平直边界.上述试验结果表明，地壳变形带信息识别和提取方法的理论是正确的.

4 在桐柏—大别地区的应用效果

桐柏—大别地区实测区域布格重力异常示如图2a，东经与北纬方向点距分别为0.05°和0.04°.以东部郯庐断裂（宿松—庐山沿线）为界，负异常覆盖了桐柏—大别地块的主体，中心位于罗田岳西一带.该负异常带以南的大别山南缘前陆盆地及扬子克拉通北缘均对应正异常.北淮阳及其北部的华北盆地（信阳—舒城沿线以北）主要对应正异常带，但内部含有尺度较小的负异常.图2b显示桐柏—大别地区布格重力异常的水平总梯度，断裂或边界位置在图上均表现为重力异常梯级带形式，反映出该区构造线以近东西、北西及北东向为主，但是梯级带较宽且幅度大小不一，不利于构造边界的准确定位.

为了验证地壳变形带信息识别方法有效性，将重力异常表面网格插值，点距为0.005°.并采用0.02°滑动窗口半径（计算刻痕的脊形化系数Λ时，采用0.05°窗口半径）对桐柏—大别地区布格重力异常表面进行信息提取，提取结果见图3和图4a.图3显示桐柏—大别地区重力异常表面刻痕的脊形化系数Λ分布，延伸范围长且细而强的Λ值异常反映了研究区上地壳构造变形带的分布.据此进一步划出研究区次级大陆构造单元间的边界与地质上划分的边界吻合（杨文采等，2005），属于同一构造单元内的刻痕的脊形化系数Λ具有均匀或者变化不大的分布特征.图3给出的桐柏—大别地区地壳变形带信息相当清楚，大地构造单元分区的信息丰富.华北地区整体刻痕的脊形化系数较大，变形复杂且程度较强；北部北淮阳地区，变形带较宽，主要为高Λ值覆盖，反映出该区变形方向多样，整体构造变形强烈；以信阳—商城与梅山—舒城断裂为北界，桐柏—定远与晓天—磨子潭断裂为南界的带状区域内Λ值呈现一低值带，往东Λ值增大且呈北东向分布特征，与其北部构造单元内Λ值的南北向分布特征相异，反映了印支期南北碰撞缝合带（杨文采等，2005）.南大别和北大别之间存在一条较细但很明显的高Λ值异常线，对应于南、北大别之间的分界，即晓天—磨子潭断裂.南大别整体被较低的Λ值覆盖，反映该单元地壳强度较大，内部构造变形程度稍弱，其区内的罗田穹窿也依稀可见.大别山南缘前陆盆地内，刻痕的脊形化系数Λ值整体较大，呈近东南向分布特征，反映该盆地内构造变形剧烈，构造线以近东南方向为主.位于该区东部的郯庐断裂带变形带较宽，变形程度较强.图4a显示桐柏—大别地区经过增强的边界脊形化系数分量MΛa（由于实际数据中边界在其走向上的梯度不为0，因而边界脊形化系数分量MΛa可代替边界脊形化系数MΛ），较大的MΛa值反映异常体的边界，其中，稍大的MΛa值反映变形带的边界可能扭曲或者发生汇聚（如位置a），稍小的MΛa值指示变形带中的平直边界（如位置b）.与水平梯度异常（图2b）相比，边界脊形化系数分量MΛa不仅紧缩了重力梯度带的宽度，准确地刻画了研究区内大中型断裂（图中字母a，b，c标明），而且还清晰的显示了一些小型断裂的平面位置，更加有利于构造单元划分与定位.结合地质资料（钟增球等，2001；杨文采和于常青，2001；Yang et al.，2005；Wang，2006），根据地壳变形带信息识别方法所提取的桐柏—大别地区清楚、详细的地壳变形带及构造边界信息，对该区构造单元进行了划分.划分的桐柏—大别造山带的分区见图4b.与前人一样，将桐柏—大别地区主要划分为五个构造单元（I～V），分别为北部北淮阳地区、北淮阳构造带、超高压单元、大别山造山带核部杂岩单元及大别山南缘前陆盆地.虽然构造单元分区与先前地质学家的构造分区基本一致，但是构造边界或者断裂带的位置有所差别，这是因为地质上孤立的露头只反映边界或断裂带在地表出露的位置，而根据重力场特征提取的边界是地壳不同深度上物质的综合体现.由于地壳变形带识别方法提取的边界脊形化系数分量MΛa具有细而强且连续等的特点，因而由其刻画的构造边界及断层的位置及形态更加准确与细致.

图2 桐柏—大别地区布格重力异常（a）及其水平总梯度异常（b）Fig.2 （a）Bouguer gravity anomalies in the Tongbai-Dabie area；（b）Total horizontal gradient anomalies of the data in（a）

5 结论

本文基于以随机过程理论为基础的表面刻痕识别技术，研究并提出地壳变形带信息智能识别的一种方法.理论模型数据试验结果表明了本文的地壳变形带信息识别方法与提取理论正确.桐柏—大别地区的重力场数据试验表明，位场表面刻痕的脊形化系数Λ能很好地反映地壳变形带和构造单元边界，为地壳构造单元分区提供了丰富的信息.增强的边界脊形化系数分量MΛa勾勒的边界细而强，更有利于对地壳变形带的准确定位.然而，后者虽然利于边界的准确定位，但是不分大小和主次，丧失了前者所包含的部分信息.综合以上两种图件，本文地壳变形带信息识别方法便于提取地壳变形带与构造单元边界信息，为地壳构造单元的划分提供客观的依据与标准.

图3 桐柏—大别地区重力场刻痕的脊形化系数ΛFig.3 The ridge coefficientΛshowing crustal scores in Tongbai-Dabi

地壳变形带信息提取的结果主要反映了已定形的板块缝合带、地块碰撞带及大型走滑断裂带，但是有些地壳变形带并没有清楚的反映，以后将在大区域位场数据的地壳变形带信息提取中作更仔细的研究.另外，本文主要讨论利用二阶谱矩及相应的参数对区域布格重力异常表面进行信息提取，并未涉及可能对应更多的地质信息的更高阶谱矩及相应的参数，也将在今后工作中进一步研究.

致谢 特别感谢中国地质科学院地质研究所曾祥芝助理研究员对公式推导及程序方面的指导与帮助.

Bosc hetti F，Therond V，Hornby P.2004.Feature removal and isolation in potential field data.Geophys.J.Int.，159（3）：833-841.

Chen Y D.2003.Inversion of gravity anomaly with continuous complex potential wavelet transform.Geophys &Geochem.Explor.（in Chinese），27（5）：354-361.

Chen Z X.2012.The curvelet transform and its application to information extraction for potential data ［Ph.D.thesis］（in Chinese）.Beijing：China University of Geosciences.

Clarke G K C.1969.Optimum second-derivative and downwardcontinuation filters.Geophysics，34（3）：424-437.

Cooper G R J，Cowan D R.2006.Enhancing potential field data using filters based on the local phase.Comput.Geosci.，32（10）：1585-1591.

Cooper G R J，Cowan D R.2008.Edge enhancement of potentialfield data using normalized statistics.Geophysics，71（3）：1-4.

Cordell L.1979.Gravimetric expression of graben faulting in Santa Fe county and the Espanola basin，New Mexico.30th Field Conf.New Mexico Geol.Soc.，59-64.

Dean W C.1958.Frequency analysis for gravity and magnetic interpretation.Geophysics，23（1）：97-127.

GuspíF，Introcaso B.2000.A sparse spectrum technique for gridding and separating potential field anomalies.Geophysics，65（4）：1154-1161.

Hou Z Z，Yang W C.1997.Wavelet transform and multi-scale analysis on gravity anomalies of China.Acta Geophysica Sinica（in Chinese），40（1）：85-95.

Huang Y Y.1984.The characterization of three-dimensional radom surface topography.Journal of Zhejiang University （in Chinese），1984，18（2）：138-148.

Huang Y Y.1985.Geometrical interpretation and graphical solution of second order spectrum moments and statistical invariants for random surface characterization.Journal of Zhejiang University（in Chinese），19（6）：143-153.

Li C G，Dong S，Zhang G X.2000.Evaluation of the anisotropy of machined 3Dsurface topography.Wear，237（2）：211-216.

Liu T Y.2007.New Data Processing Methods for Potential Field Exploration（in Chinese）.Beijing：Science Press.

Longuet-Higgins M S.1962.The statistical geometry of random surfaces.Hydrodynamic Instabity.13th Sympo.Applied Mathem.Amer.Math.Soc.，105-142.

Miller H G，Singh V.1994.Potential field tilt—a new concept for location of potential field sources.J.Appl.Geophys.，32（2-3）：213-217.

Nayak P R.1973.Some aspects of surface roughness measurement.Wear，26（2）：165-174.

Raiche A.1991.A pattern recognition approach to geophysical inversion using neural nets.Geophys.J.Int.，105（3）：629-648.Thomas T R.1987.Rough Surfaces （in Chinese）.Zhou G R Trans.Hangzhou：Zhejiang University Press.

Wang Y.2006.The onset of the Tan-Lu fault movement in eastern China：constraints from zircon（SHRIMP）and40Ar／39Ar dating.Terra Nova，18（6）：423-431.

Wang Y G，Zhang F X，Wang Z W，et al.2013.Edge detection of potential field using normalized differential.Journal of Jilin University （Earth Science Edition）（in Chinese），43（2）：592-602.

Yanagi K，Hara S，Endoh T.2001.Summit identification of anisotropic surface texture and directionality assessment based on asperity tip geometry.International Journal of Machine Tools and Manufacture，41（13）：1863-1871.

Yang S Z，Wu Y，Xuan J P，et al.2007.Time Series Analysis in Engineering Application（Vol.2）（in Chinese）.Wuhan：Huazhong University of Science &Technology Press.

Yang W C.1997.Geophysical inverse theroy and method.Beijing：geological publishing house.

Yang W C，Shi Z Q，Hou Z Z，et al.2001.Discrete Wavelet transform for multiple decomposition of gravity anomalies.Chinese J.Geophysics（in Chinese），44（4）：534-541.

Yang W C，Xu J R，Cheng Z Y，et al.2005.Regional Geophysics and Crust-Mantle Interaction in Sulu-Dabie Orogenic Belt（in Chinese）.Beijing：Geological Publishing House.

Yang W C，Yu C Q.2001.Kinetics and dynamics of development of the Dabie-Sulu UHPM terranes based on geophysical evidences.Chinese J.Geophysics（in Chinese），44（3）：346-359.

Zhong Z Q，Suo S T，Zhang H F，et al.2001.Major constituents and texture of the Tongbai-Dabie collisional orogenic belt.Earth Science （in Chinese），26（6）：560-567.

附中文参考文献

陈玉东.2003.复小波变换反演重力异常.物探与化探，27（5）：354-361.

陈召曦.2012.位场数据的曲波变换与信息提取应用［博士论文］.北京：中国地质大学.

侯遵泽，杨文采.1997.中国重力异常的小波变换与多尺度分析.地球物理学报，40（1）：85-95.

黄逸云.1984.三维随机表面形貌的识别.浙江大学学报，18（2）：138-148.

黄逸云.1985.随机表面二阶谱矩和统计不变量的几何解释及其图解法.浙江大学学报，19（6）：143-153.

刘天佑.2007.位场勘探数据处理新方法.北京：科学出版社.

托马斯T R.1987.粗糙表面：测量、表征及其应用.周广仁译.杭州：浙江大学出版社.

王彦国，张凤旭，王祝文等.2013.位场归一化差分法的边界检测技术.吉林大学学报（地球科学版），43（2）：592-602.

杨叔子，吴雅，轩建平等.2007.时间序列分析的工程应用（下）.武汉：华中科技大学出版社.

杨文采.1997.地球物理反演的理论与方法.北京：地质出版社.

杨文采，施志群，候遵泽等.2001.离散小波变换与重力异常多重分解.地球物理学报，44（4）：534-541.

杨文采，徐纪人，程振炎等.2005.苏鲁大别造山带地球物理与壳幔作用.北京：地质出版社.

杨文采，于常青.2001.根据地球物理资料分析大别—苏鲁超高压变质带演化的运动学与动力学.地球物理学报，44（3）：346-359.

钟增球，索书田，张宏飞等.2001.桐柏—大别碰撞造山带的基本组成与结构.地球科学，26（6）：560-567.