断层阶区对震源破裂传播过程的控制作用研究

袁杰，朱守彪，2

1中国地震局地壳应力研究所（地壳动力学重点实验室），北京 100085

2中国科学院计算地球动力学重点实验室，北京 100049

1 引言

地震断裂带通常是由一系列几何形态复杂、空间上不连续的断层段所组成.断裂带中，若2条断层走向平行、中间有一定的间距，这样的走滑断层系统称为断层阶区（stepover）（Rodgers etal.，1980）.断层阶区对地震破裂有重要影响：一方面，断层阶区有可能阻止地震破裂由一条断层向另一条断层传播，成为地震破裂的障碍体（Wesnousky，2006）；但在一定条件下，地震破裂也可能会跳跃断层阶区，从而形成更大震级的地震（Wesnousky，2006）.由于地震震级与破裂总长度直接相关.所以，若断层阶区对破裂起阻碍作用，导致地震破裂终止，那么破裂总长度就小，相应的地震震级就低；反之，若破裂能够穿越断层阶区传播，则破裂总长度就会大，这样地震震级就高.因此，定量分析地震破裂能否穿越断层阶区而形成大地震对于地震学研究及灾害评估等有重要的科学意义及应用价值.

实际观测发现，不少大地震在破裂过程中，出现了破裂从一个断层跳跃传播至另一个断层，即跨越断层阶区继续传播的现象，如：2001年的昆仑山口西地震（Antolik etal.，2004），2004年的印尼大地震（Bilham，2005），2008年汶川地震（Shen etal.，2009），2010年智利地震（Lay，2011）和日本大地震（Stein and Okal，2011）等.此外，不少研究人员对断层阶区影响地震破裂传播的因素进行了定量分析，如：Harris等（1991）使用有限差分的方法来分析拉张阶区和挤压阶区之间的不同，分析结果表明第1条断层破裂结束到第二条断层开始发生破裂，拉张阶区所需要的间隔时间较挤压阶区更长.Oglesby（2005）利用有限元方法对走滑断层阶区间夹着一段倾滑断层的地震破裂过程进行了模拟，发现由于这一段倾滑断层的存在会极大地增加破裂跳跃断层阶区传播的可能性，从而导致更大地震的发生.Finzi和Langer（2012）通过远场加载及改变断层端部的动摩擦系数，来改变断层阶区的库仑应力状态，实现模拟地震破裂越过断层阶区的传播情况，发现软弱断层带及断层界面不同材料都会促使破裂传播，从而增加破裂跳跃断层阶区传播的可能性.Ryan（2012）利用FaultMod有限元程序模拟破裂穿过断层阶区的情况，并对比了滑移弱化、速率-状态相关摩擦关系对破裂跳跃阶区传播的影响.

尽管前人对断层破裂跳跃阶区传播的现象做了大量的研究，但很少有人对影响破裂跳跃阶区传播的具体因素进行深入的分析.本文利用不连续变形体接触力学的动态有限单元方法，模拟断层阶区对地震破裂传播的控制作用，定量分析初始应力场、摩擦关系及断层阶区间距等对断层破裂跳跃阶区传播的影响.

2 计算原理及有限元模型

2.1 物理方程

2.1.1 运动方程

断层自发破裂问题的有限元动力学方程如下：

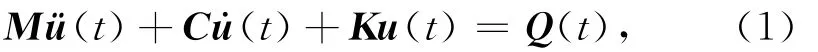
上式中ü（t）、u（t）和u（t）分别是系统的节点加速度向量、节点速度向量和节点的位移向量.M，C，K和Q（t）分别是系统的质量矩阵、阻尼矩阵、刚度矩阵、和节点荷载向量.式中：

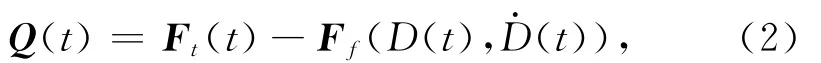
式中Ft（t）和Ff（D（t），D（t））分别表示构造力和断层面上的接触力，D表示断层上的相对滑移距离，D 表示断层上的相对滑移速率.实际上，模型使用的物理方程与袁杰和朱守彪（2014）所使用的相同，此处不再赘述.

另外，断层面上节点的运动状态满足库仑摩擦准则（Zienkiewicz etal.，2005）：

上式中σn为法向接触应力，τ为切向应力，μ为摩擦系数.

2.1.2 摩擦本构关系

断层上的摩擦关系非常复杂（Dieterich，1994；Scholz，1998，2002；Tse and Rice，1986）.前人已尝试使用多种类型的摩擦关系来模拟断层的自发破裂过程（Lapusta etal.，2000；Shi etal.，2008；Zhang and Chen，2006a，b）.但是，在所有类型的摩擦关系中，滑移弱化的摩擦本构关系由于其形式简单且易于实现得到非常广泛的应用.这种摩擦关系最初是由Ida（1972）、Palmer和Rice（1973）及Andrews（1976a，b）提出.后来，Ohnaka等（1989，1993，1996，1999）也在实验研究中证实了断层上的摩擦系数随断层两侧相对滑移距离增大而减小的真实性.因此本文中的所有模型均采用这个摩擦关系，其数学表达式如下（Andrews，1976a，b；Ida，1972；Palmer and Rice，1973）：

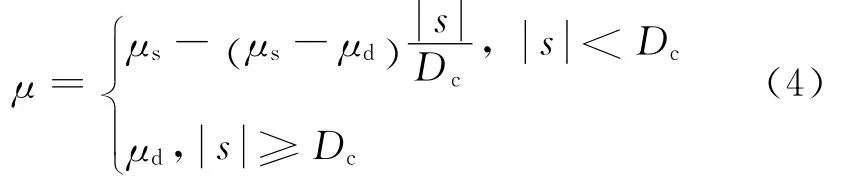
上式中μs为静摩擦系数，μd为动摩擦系数，s为断层面上两点之间的相对滑动距离，Dc为特征滑动距离.

2.2 时间积分方法

时间积分方法是非线性有限元计算中的重要方面，为保证计算精度，同时兼顾计算速度，模拟计算中采用中心差分的时间积分方法（显式有限元算法）.

由于中心差分法是条件稳定算法（王勖成，2003），即时间步长Δt必须小于所求解方程性质所决定的某个临界值Δtcr.Δtcr的大小可以通过公式Δtcr＝L／（E／ρ）1／2来近似估算（式中L为模型中尺度最小单元的最小边长）.经过计算，本模型中Δtcr≈0.019s.文中实际计算中所采用的时间步长为1.0×10-3s，远小于0.019s的临界值，因而满足中心差分法的稳定性条件.可见，文中的计算过程应该是稳定、收敛的，能够满足计算精度要求.

本文利用ABAQUS／Explicit商业有限元软件（有限元显式计算程序）（Hibbitt etal.，2012）来模拟断层破裂的动力学过程，并且使用有限元分析中的接触单元技术来描述不连续断层的动力学行为，具体计算中是调用ABAQUS中的VFRIC用户子程序进行二次开发来实现模拟断层的自发破裂过程.

2.3 数值方法验证

由于断层的自发破裂过程是非线性极强的不连续变形体接触力学问题，对于边界或初始条件稍为复杂的情况还没有解析解.因此本文利用非线性有限单元方法来重复Rojas等（2008）文中的断层自发破裂结果，以验证本文数值方法的有效性及可靠性.参照Rojas等的模型，选取验证模型的空间尺度为60km×60km的正方形，断层位于模型正中间，其长度为30km.模型中的材料参数、初始应力场、摩擦系数均与Rojas等模型相同.具体数值见表1.

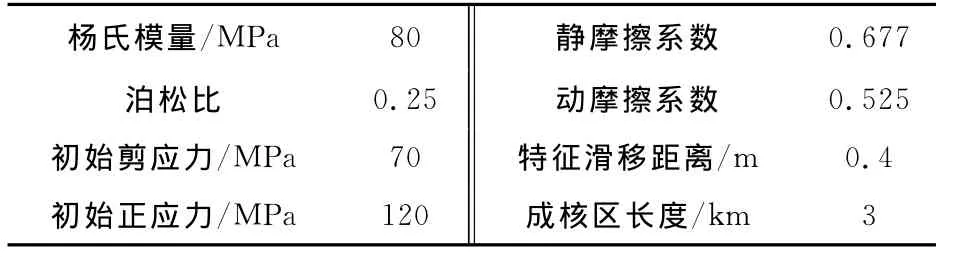
表1 模型中的材料参数、初始应力场及摩擦系数Table 1 Model material parameters，initial stress field and friction coefficients

同Rojas等（2008）的模型一样，为让断层能够产生自发破裂行为，模型在断层中央设置了成核区.在成核方式上，本文与Rojas等的模型略有不同：本文通过降低成核区上的摩擦系数实现成核，发生自发破裂行为，而Rojas等的模型通过增加成核区的初始剪应力来实现这一过程.尽管成核方式不同，但实现断层自发破裂的效果是等同的.

图1是模型计算的、断层上一典型位置（离成核区中心12.5km处）的相对滑移速率、相对滑移距离以及剪切应力随时间的变化过程.对照图1给出的相对滑移速率、相对滑移距离、剪切应力随时间变化曲线与Rojas等文中的图（原文中图10—12）可以看出，两者变化格局基本相同，只是某些细节略有变化.出现两模型结果不完全一样的原因可能是：算法不同（Rojas等（2008）使用的是限差分方法）、成核方式不同以及网格剖分不同等.

总之，通过模型检验可以看出，本文所采用的非线性有限元方法完全可以用来模拟断层的自发破裂过程，可以定量研究断层阶区对破裂传播的影响.

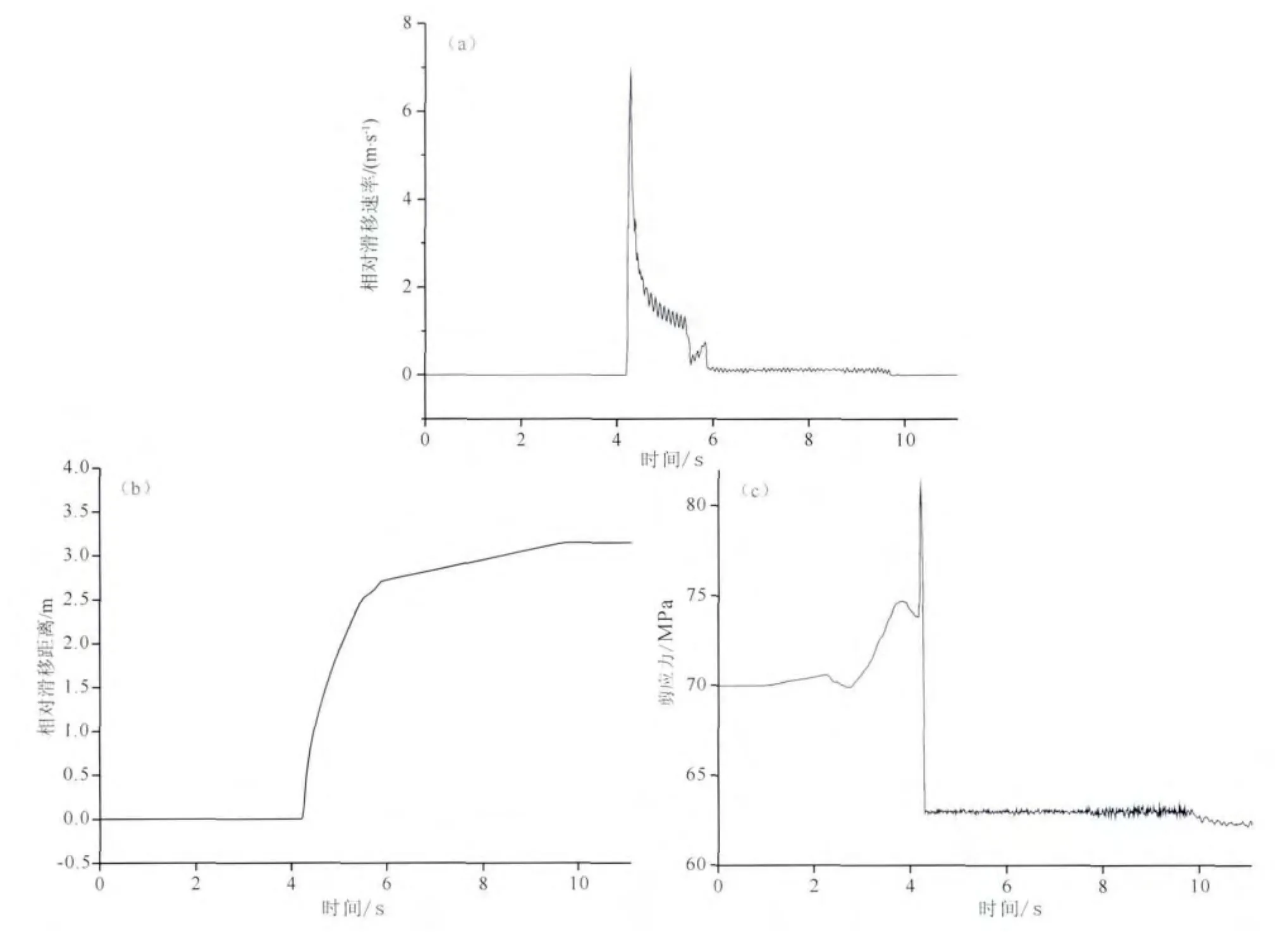
图1 断层上一典型点（离成核区中心12.5km）的相对滑移速率（a）、相对滑移距离（b）、剪切应力随时间的变化（c）Fig.1 Slip velocity（a），sliding distance（b），and shear stress（c）at a typical point on the fault（12.5km from the center of the nucleation patch）vary with time

3 计算结果

3.1 有限元模型

实际地震的断层几何是非常复杂的（如：2001年发生的昆仑山口西地震（Antolik etal.，2004），2008年汶川地震（Shen etal.，2009）等），一般会发生弯曲、拐折、分叉等现象，特别是出现断层阶区.为减少计算量，从而更容易研究断层阶区对地震破裂传播过程的控制作用，将实际断层的三维情况抽象为二维模型，并将断层简化为直线（见图2）.图2为研究所用的模型几何及初始、边界条件.由图可见，模型空间尺度为150km×150km的正方形，直线AB为断层1所在位置，直线CD为断层2所在位置，阶区重叠长度a＝10km，断层间距为b（其值约为1～5km）.同前人的研究一样（如：Shi etal.，2008；Olsen-Kettle etal.，2008；袁杰和朱守彪，2014），为让断层能够产生自发破裂行为，本研究通过成核来实现断层的自发破裂过程.模型在断层中央设置了成核区L（见图2），这段区域的应力状态在发生破裂开始前就已达到或超过破裂准则所要求的临界状态，其长度Lnucl＝2km.为防止地震波通过边界反射而影响结果，模型在四周设置了吸收边界（图2中灰色部分）.此外，在整个区域内施加初始应力场并在外部边界Γ上加载统一的正应力σ和剪应力τ.

模型全部采用3节点单元来剖分，以此来完全消除沙漏现象对模型计算产生的影响（Hibbitt etal.，2012）.断层为研究的重点区域，为了保证精度，在该区域对网格进行细化，单元边长为100m.此外，随着离开断层距离的增大，单元的尺度也越来越大，模型最外围部分单元的边长为500m.这样整个模型的有限模型的节点数为373338，单元数为742994.模型四周的吸收边界采用的是无限元单元（Hibbitt etal.，2012）.

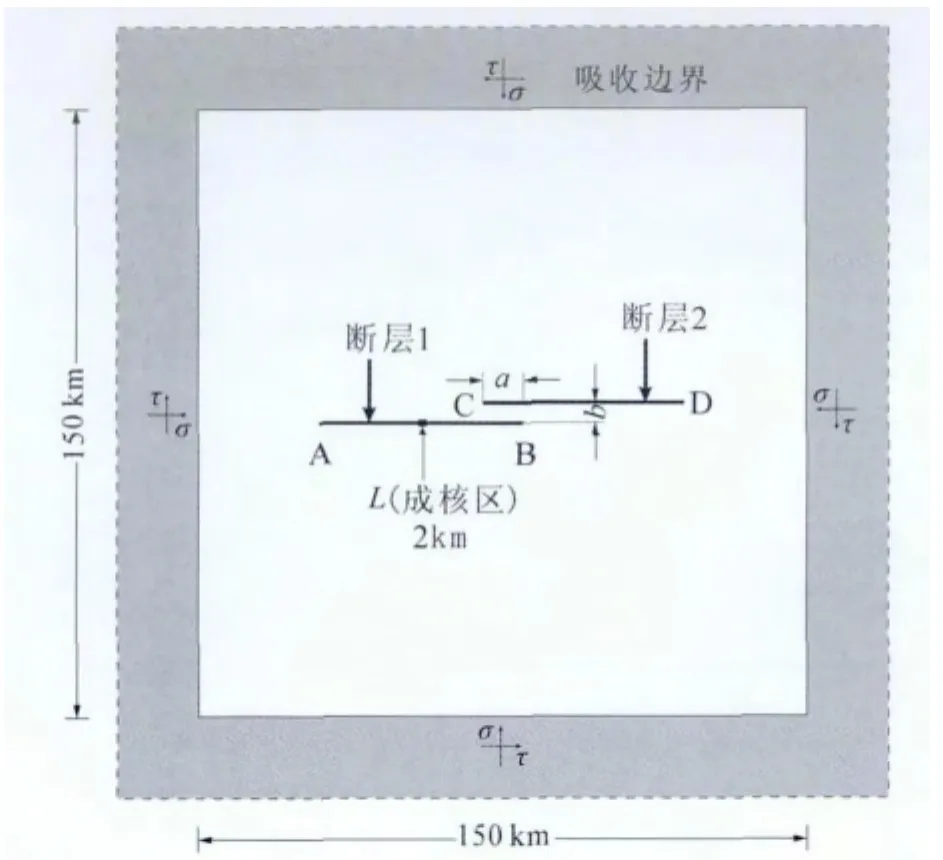
图2 模型的几何及初始、边界条件模型几何为150km×150km的正方形.图中直线AB表示断层1位置，直线CD表示断层2位置，箭头所指的粗黑线L为成核区，其长度为Lnucl＝2km，四周灰色部分为吸收边界.Fig.2 Model geometry，the initial and boundary conditions The model domain is 100km by 100km.Line AB in the figure is the location of fault 1，line CD is the location of fault 2，the bold black line L to which the arrow points is the nucleation zone，its length is Lnucl＝2km，the gray region around the model is absorbing boundary.

由于本文重点是研究初始应力状态、摩擦关系以及阶区间距对断层破裂跳跃阶区传播过程的影响，为简单起见，模型中的介质选取为各向同性的线弹性材料.杨氏模量取为E＝7.5×1010Pa、泊松比ν＝0.28和密度为ρ＝2700kg·m-3，由材料的P波速度（α）、S波速度（β）、瑞利波速度（CR）与杨氏模量E、泊松比ν和密度ρ的关系计算可得α＝5959m·s-1，β＝3294m·s-1，CR＝3045m·s-1.

数值模拟及实验室研究表明，断层的自发破裂是否向外传播、破裂传播速度及破裂模式受应力场状况和摩擦本构关系的影响较大（袁杰和朱守彪，2014）.Wesnousky（2006）指出断层破裂能否跳跃阶区从一个断层传播至另一个断层，与阶区间距有很大的关系.因此为研究断层破裂在经过阶区时的传播情况，本文根据不同的初始应力状态、不同的摩擦本构关系以及不同的阶区间距，进行了反复的数值实验，以探究不同因素对断层破裂跳跃阶区传播的影响.模型参数的设置具体如下：

所有模型中的初始正应力均为100MPa；初始剪应力分别为54MPa、56MPa、58MPa三种应力状态；静摩擦系数有0.6和0.58两种；动摩擦系数有0.5、0.52、0.54、0.56四种；断层阶区间距有1km、3km、5km三种情况.本文利用控制变量法来研究每一种因素对断层破裂跳跃阶区传播的影响，因此对上述几种因素进行了不同的组合，形成多种模型，通过对比这些模型的模拟结果来探究这些因素的具体控制作用.

3.2 断层破裂经过断层阶区的传播过程

为展示破裂能否跳跃断层阶区、从一个断层传播至另一个断层的具体过程，首先给出2个具体实例.模型1与模型2的初始应力场相同，不同的只是滑移弱化摩擦本构关系中的动摩擦系数.

3.2.1 模型1

模型1中，初始应力场为：σ＝100MPa，τ＝54MPa；摩擦本构关系中的参数：μs＝0.6，μd＝0.5，Dc＝0.1m.

在上述条件下，通过有限元计算发现，断层1首先在成核区（断层1的中心）开始出现破裂，然后逐步向左右两侧自发传播.图3是断层1两侧的相对滑动距离随时间的变化.图中可见，断层上各点在开始破裂后两边的相对滑移距离逐渐增大，断层上的最大滑移距离为3.74m；滑移以成核中心呈对称分布，断层破裂由中心传至右端终止，历时8.6s.通过计算，得出平均破裂速度为2907m·s-1，低于S波传播速度，属于亚剪切破裂.此外，图4给出了断层2两侧的相对滑移随时间的变化.从图中可以看出，从断层1开始破裂后的8.75s时，断层2开始从离左边端部约10km处成核，产生自发破裂，然后向左右两侧传播.且图4还显示，当断层1破裂完毕后，断层2不是立即发生破裂，而是这中间有一个0.15s的时间延迟.本模型中破裂在跳跃断层阶区出现的时间延迟现象与Harris等（1991，1993）的结果一致.产生时间延迟现象的原因，主要是断层1完全破裂后，尽管断层面上破裂终止传播，但断层上位错的累积导致断层端部应力在一段时间内持续增大，应力波不断向外传播.当应力波到达断层2时，应力在断层2的断面上积累，随着时间的增加，应力不断增大；一旦断层2的应力增大到破裂强度时，断层2发生破裂.所以导致了断层1破裂后，断层2不是马上立即就破裂的现象.需要指出的是，断层2的破裂是被断层1触发的，破裂的成核是自动形成的.

3.2.2 模型2

模型2中，初始应力场为：σ＝100MPa，τ＝54MPa；摩擦本构关系中的参数：μs＝0.6，μd＝0.52，Dc＝0.1m.与模型1不同的只是动摩擦系数不同.

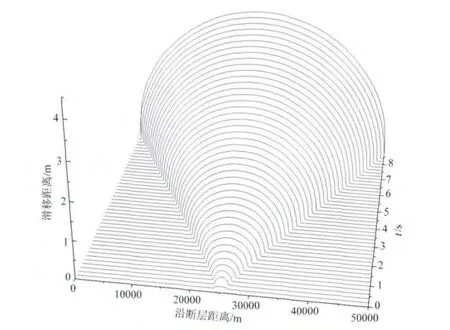
图3 模型1中断层1两侧相对滑移距离随时间的变化x轴表示沿断层距离，y轴表示滑移距离，z轴表示时间；断层上的破裂由中心不断向两边延伸.断层破裂由中心传至整个断层总共历时8.6s，在8.6s时断层上的最大滑移距离为3.74m.Fig.3 Snapshots of the slip profiles along the interface 1various times for Model 1 The xaxis represents the position along the strike，yaxis denotes the slip，and zaxis stand for time.Rupture on the fault continuously extends out from the center of the fault along both opposite directions.Rupture propagates from the center to the end of the fault within 8.6s，and the maximum slip on the fault reaches 3.75mwhen the whole process ends.

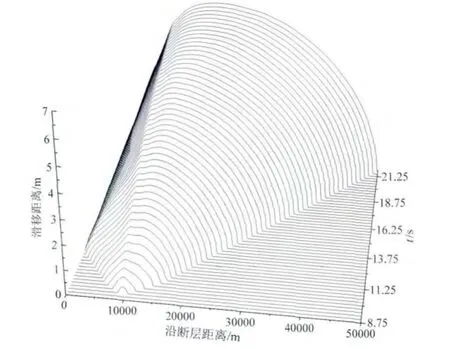
图4 模型1中断层2两侧相对滑移随时间的变化x轴表示沿断层距离，y轴表示滑移距离，z轴表示时间.在8.75s时，断层从离左边端部约10km处开始产生自发破裂，然后逐步向左右两侧传播.由于断层2左侧较短，因此破裂是不对称的.Fig.4 Snapshots of the slip profiles along the interface 2various times for Model 1 The xaxis represents the position along the strike，yaxis denotes the slip，and z axis stand for time.The spontaneous generation of rupture begins at 10km from the left end of the fault at the time of 8.75s，then the rupture continuously extends out in both opposite directions.The propagation is asymmetry due to the shorter left side in fault 2.

在上述条件下，模拟结果显示，断层1首先在成核区开始出现滑移，然后逐步向左右两侧产生自发破裂.图5是断层1两侧的相对滑移随时间的变化情况（类似于图3）.从图中可以看出，断层上各点在开始破裂后两边的相对滑移逐渐增大，断层上的最大滑移量为2.2m；此外，滑移以成核位置为中心呈对称分布.整个断层破裂完毕历时9.2s，通过计算得出平均破裂速度为2717m·s-1，仍低于S波传播速度，也属于亚剪切破裂.同样，图6给出了断层2两侧的相对滑移随时间的变化.从图中可以看出，断层面上的滑移为0，自始至终断层都未发生破裂.可见，断层1上的破裂没有跳跃传播至断层2上.

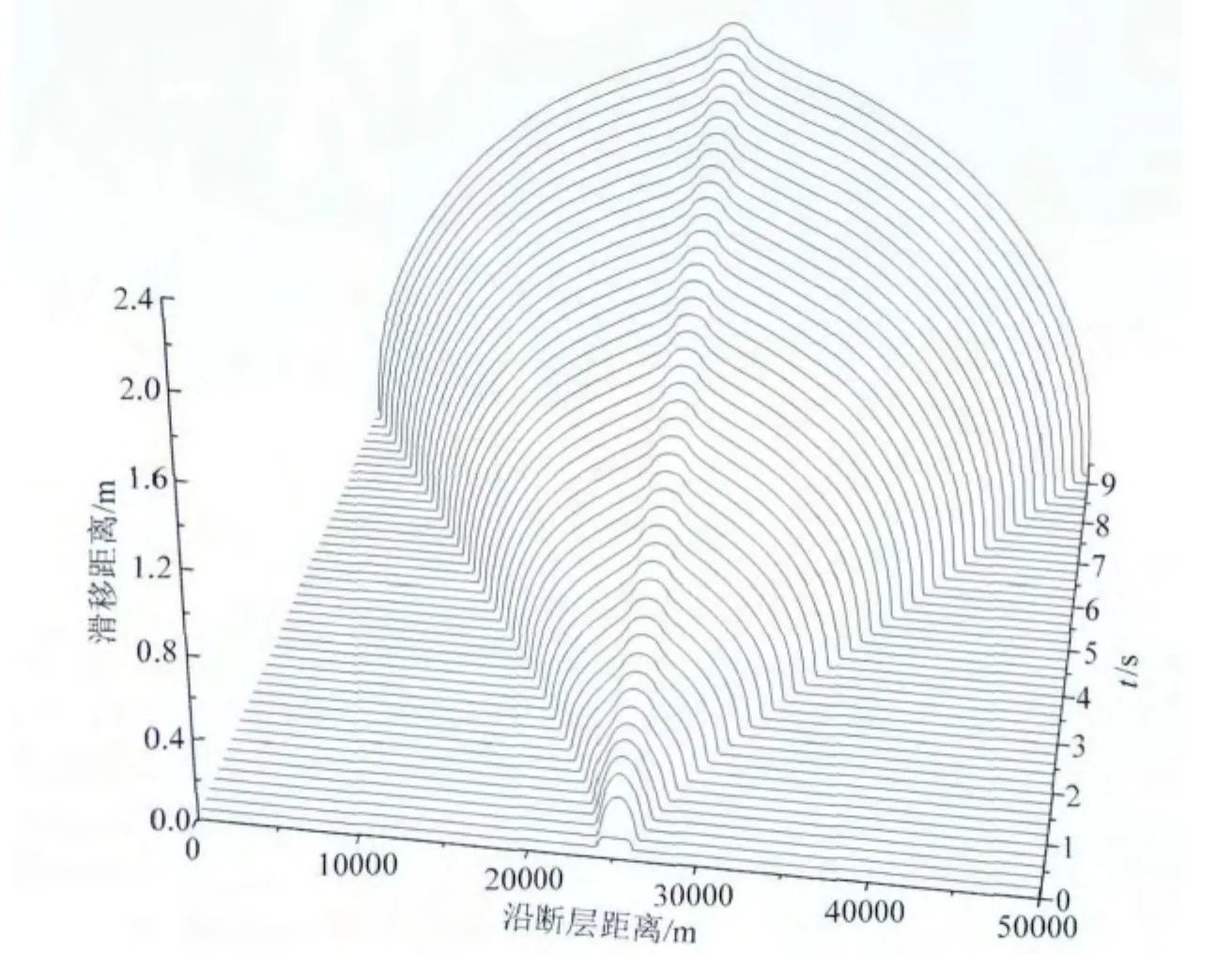
图5 模型2中断层1两侧相对滑移距离随时间的变化x轴表示沿断层距离，y轴表示滑移距离，z轴表示时间；断层上的破裂由中心不断向两边延伸.断层破裂由中心传至整个断层总共历时9.2s，在9.2s时断层上的最大滑移距离为2.2m.Fig.5 Snapshots of the slip profiles along the interface 1various times for Model 2 The xaxis represents the position along the strike，yaxis denotes the slip，and zaxis stand for time.Rupture on the fault continuously extends out from the center of the fault along both opposite directions.Rupture propagates from the center to the end of the fault within 9.2s，and the maximum slip on the fault reaches 2.2mwhen the whole process ends.

图6 模型2中断层2两侧相对滑移距离随时间的变化x轴表示沿断层距离，y轴表示滑移距离，z轴表示时间.图中显示，断层上的滑移均为0，可见断层没有发生破裂.Fig.6 Snapshots of the slip profiles along the interface 2various times for Model 2 The xaxis represents the position along the strike，yaxis denotes the slip，and zaxis stand for time.It shows all slips on the fault are 0，so no rupture is generated on the fault.

通过比较以上2个模型，可以看出，在初始应力场、静摩擦系数和阶区间隔相同时，动摩擦较大者不利于破裂跳跃断层阶区，此时断层阶区阻止破裂继续传播，成为地震的终止位置；相反，对于动摩擦系数较小的断层，破裂将容易跳跃阶区继续传播，从而有可能导致更大震级的地震发生.

3.3 决定破裂跳跃断层阶区的控制因素

3.3.1 影响破裂继续传播的主要因素分析

上面分析了由于动摩擦系数不同而导致断层破裂经过断层阶区时的两种不同情形.为较全面地研究决定破裂跳跃断层阶区的主要控制因素，下面我们将考虑更多的因素，考察初始应力场、摩擦本构关系（动、静摩擦系数）、阶区间隔大小对于破裂跳跃传播过程的影响.计算中模拟了几十种不同模型进行了详细分析，表2给出了其中16种典型情况.由于本文主要研究断层阶区对破裂传播的影响，因此在这些模型中没有展示详细的破裂过程.表2只指示断层阶区是阻止破裂传播还是让其破裂继续传播的情况.

根据表2的实验结果，断层阶区对破裂过程的影响有以下几种情况：

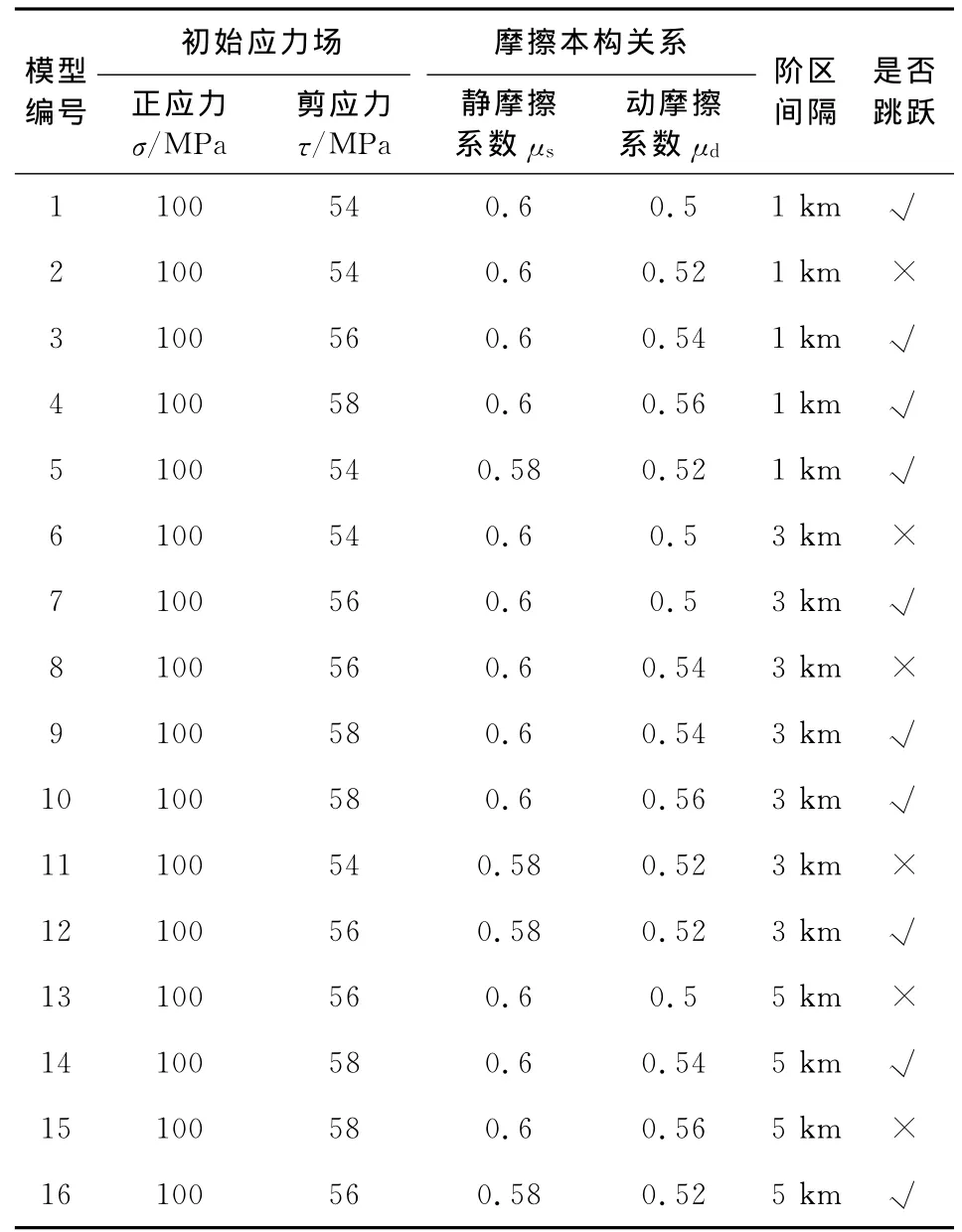
表2 不同模型的初始应力场、摩擦本构关系及不同阶区间隔时的模拟结果Table 2 Simulation results in different models in which initial stress fields，friction laws，widths of stepover are different

①比较模型2和模型5，我们可以看出，在其他条件相同时，当断层上的静摩擦系数越大，断层破裂越不易穿越阶区.

②比较模型1和模型2、模型7和模型8以及模型14和模型15，可以看出断层上的动摩擦系数对破裂能否跳跃阶区的影响一致，其值越大破裂越不易发生跳跃传播.

③比较模型6和模型7、模型8和模型9以及模型11和模型12，可以看出，当初始剪应力越大，即断层周边初始剪应力与初始正应力的比值越大，断层破裂越容易跳跃阶区传播.

④比较模型1和模型6、模型3和模型8、模型4和模型15、模型5与模型11、模型7和模型13以及模型10和模型15，可以看出当阶区间距越大，断层破裂越不易跳跃阶区传播.由此可知，当区域内断层段之间的相隔距离越小，破裂越容易跳跃而发生大的地震.

由上述分析可见：断层上的摩擦系数减小或断层周边区域内的初始剪应力增大时，都将导致断层破裂跳跃阶区传播的可能性.此外，当断层阶区间距越小，断层破裂也越容易跳跃阶区传播.

3.3.2 破裂传播的机制分析

通过以上的对比分析可知，断层面上的摩擦关系等模型参数对破裂通过阶区传播具有重要的影响.但这是通过模拟实验总结出来的一些现象，下面从力学的角度来定量分析发生上述现象的主要原因.

由于模型中决定断层是否破裂是根据库仑破裂准则，因此下面利用库仑破裂准则来分析破裂跳跃阶区的传播机制.

根据公式（3），两断层面开始滑动之前，其断层上可以承受某一大小的剪应力，这种状态称为闭锁状态（粘合）.库仑摩擦定律定义了一个极限剪应力τlim，当断层面上的剪应力τ达到τlim时，断层便开始滑动，这种状态称为滑动状态（或破裂）.在本文中，τlim＝μσn，其中，μ表示摩擦系数，σn表示断层面上的法向应力.

因此根据库仑破裂假设，岩石趋近于破裂状态的库仑破裂应力σf为

其中τ为断层面上的剪应力，μs为断层面上的静摩擦系数，σn为断层面上的法向应力.当断层所在区域内的σf＞0时，表明断层将会发生破裂，否则断层处在闭锁状态.

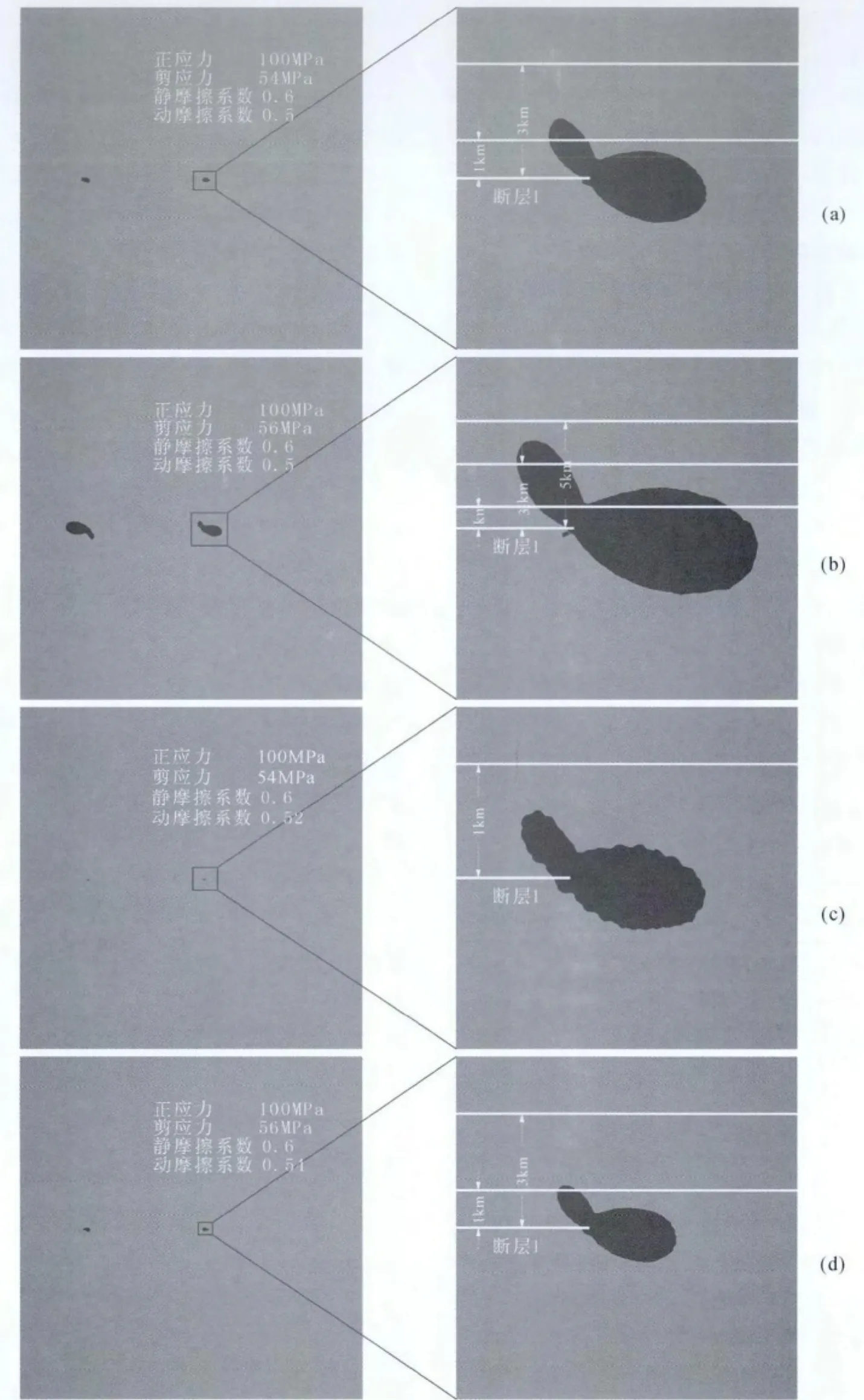
图7 断层1完全破裂后断层周边的库仑应力云图其中左边一列图显示的是整个模型的库仑应力云图，右边一列图是断层1右端放大的库仑应力云图.黑色区域表示σf＞0，灰色区域表示σf＜0，最底下一条白线表示断层1所在位置，其他白线分别表示离断层1的距离为1km、3km及5km断层2可能出现的位置.若断层2出现在黑色区域里，则破裂可以越过阶区继续传播；否则断层2不能发生破裂.Fig.7 The Coulomb stress distribution around the fault 1when the rupture finished completely The left side illustrate the Coulomb of whole model.The right column is the amplified Coulomb stress distribution of the right end of fault 1.The black represent the area whereσf＞0，while the gray denote the area whereσf＜0.White lines on the bottom indicate the location of fault 1，and other yellow lines indicate the possible position of fault 2，which probably is 1km，3km or 5km from fault 1.If fault 2appears in black area，then that the rupture could jump the stepover and extend；if not，the rupture will be arrested.

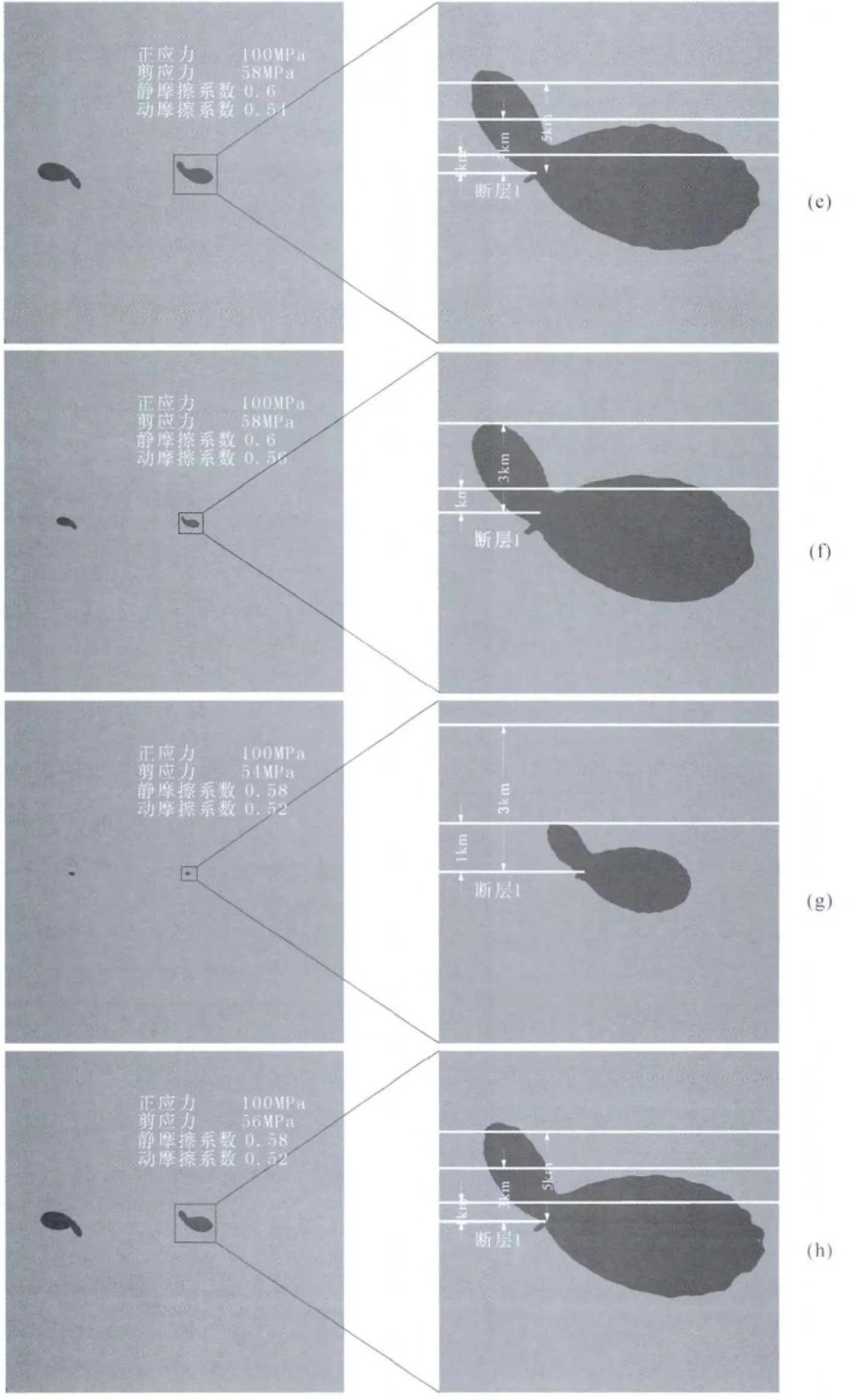
图7 续Fig.7 Continue

图7 为在断层1完全破裂后断层周边的库仑应力等值线云图.黑色区域表示σf＞0，灰色区域表示σf＜0，根据库仑破裂准则可知当断层1完全破裂后，若断层2某一部分落入黑色区域，则根据库仑准则，断层2将被触发产生自发破裂，即破裂越过断层阶区继续传播.此外，由图7可以看出，断层1破裂后，只有断层两端的库仑应力σf＞0，而断层的其他部分则σf＜0.所以断层破裂后，应力只在断层端部集中，而其他部位应力已经释放.

由图7c和图7g可以看出，当初始应力场和动摩擦系数相同时，静摩擦系数较小的断层两端引起的黑色区域较大，图7c中黑色区域未达到离断层1的距离为1km的地方，而图7g黑色区域已达到离断层1的距离为1km.由此可知当初始剪应力τ＝54MPa、静摩擦系数μs＝0.6、动摩擦系数μd＝0.54时，断层1的破裂不能触发离断层1的距离为1km的断层2的破裂；而当静摩擦系数μs＝0.58，初始应力场、动摩擦系数相同的情况下，断层1的破裂能触发离断层1的距离为1km的断层2的破裂.由以上分析可知在其他因素相同，模型中静摩擦系数较小将容易促使断层破裂跳跃阶区发生传播.

由图7（a、c）、图7（b、d）及图7（e、f）可看出，当初始应力场和静摩擦系数相同时，动摩擦系数较小的断层两端产生的黑色区域较大，即能触发断层2破裂的区域较大.通过同样的分析可知，模型中动摩擦系数较小亦容易促使断层破裂跳跃阶区发生传播.

由公式（4）中可以推断：当摩擦系数相同时，初始剪应力较大将增大σf＞0的区域范围.再由图7（a、b）、图7（d、e）及图7（g、h）也可证明这一推断的正确性.因此可知当摩擦系数相同时，初始剪应力较大容易使断层1的破裂触发断层2的破裂.

以上分析从力学角度解释了断层破裂跳跃阶区的传播机制，也进一步验证了表2的结果.

4 讨论与结论

文中利用有限单元方法对断层破裂经过断层阶区的传播情况进行了分析，给出了决定破裂能否跨越断层阶区继续传播的主要控制因素.但文中的初始应力场是均匀的、材料的物性是线弹性，实际情况比文中的模型要复杂得多.因此，对于非均匀初始场，特别是考虑重力作用及构造加载获得的应力场（朱守彪和张培震，2009；Zhu and Zhang，2013），今后应作为研究的重点，从而将地震孕育与同震破裂过程进行有机的统一结合，使得获得的破裂模型更符合实际.此外，由于应力在断层端部集中，端部介质的物性会发生变化（Duan，2008，2010；Duan and Day，2008；Shibazaki，2005）；断层两盘由于长期的地质作用，介质的物理性质会发生变化（Xia etal.，2005），因此在后续的研究中应考虑更为复杂的介质情况.

根据上述分析及模拟结果，得出以下初步结论：

断层面上的摩擦系数减小、断层周边区域内的初始剪应力增大及断层阶区间距越小，都会增加断层破裂跳跃阶区传播的可能性，断层破裂也越容易跳跃阶区继续传播，更容易出现更大的地震.相反，断层上的摩擦系数较大、初始剪应力较小、断层阶区间隔大，那么断层阶区可能会阻止破裂继续前进，断层所在位置将是断层破裂的终止区域.本研究对于认识破裂跳跃阶区传播的动力学过程及进行地震危险性分析有一定的参考价值.

致谢 十分感谢两位匿名审稿专家所提出的问题以及对文章修改所给予的建设性意见.

Andrews D J.1976a.Rupture propagation with finite stress in antiplane strain.Journal of Geophysical Research，81（20）：3575-3582.

Andrews D J.1976b.Rupture velocity of plane strain shear cracks.Journal of Geophysical Research，81（32）：5679-5687.

Antolik M，Abercrombie R E，Ekstrôm G.2004.The 14November 2001Kokoxili（Kunlunshan），Tibet，earthquake：Rupture transfer through a large extensional step-over.Bulletin of the Seismological Society of America，94（4）：1173-1194.

Bilham R.2005.A flying start，then a slow slip.Science，308（5725）：1126-1127.

Dieterich J.1994.A constitutive law for rate of earthquake production and its application to earthquake clustering.Journal of Geophysical Research：Solid Earth（1978—2012），99（B2）：2601-2618.

Duan B，Day S M.2008.Inelastic strain distribution and seismic radiation from rupture of a fault kink.Journal of Geophysical Research：Solid Earth（1978—2012），113（B12311），doi：10.1029／2008JB005847.

Duan B C.2008.Effects of low-velocity fault zones on dynamic ruptures with nonelastic off-fault response.Geophysical Research Letters，35（4），doi：10.1029／2008GL033171.

Duan B.2010.Inelastic response of compliant fault zones to nearby earthquakes.Geophysical Research Letters，37（16），doi：10.1029／2010GL044150.

Finzi Y，Langer S.2012.Predicting rupture arrests，rupture jumps and cascading earthquakes.Journal of Geophysical Research：Solid Earth（1978—2012），117（B12303），doi：10.1029／2012JB009544.

Harris R A，Archuleta R J，Day S M.1991.Fault steps and the dynamic rupture process：2-D numerical simulations of a spontaneously propagating shear fracture.Geophysical Research Letters，18（5）：893-896.

Harris R A，Day S M.1993.Dynamics of fault interaction：Parallel strike-slip faults.Journal of Geophysical Research：Solid Earth（1978—2012），98（B3）：4461-4472.

Hibbitt H，Karlsson B，Sorensen P.2012.ABAQUS Theory Manual，Version 6.12.Pawtucket，Rhode Island，USA.

Ida Y.1972.Cohesive force across the tip of a longitudinal-shear crack and Griffith′s specific surface energy.Journal of Geophysical Research，77（20）：3796-3805.

Lapusta N，Rice J R，Ben-Zion Y，Zheng G.2000.Elastodynamic analysis for slow tectonic loading with spontaneous rupture episodes on faults with rate-and state-dependent friction.Journal of Geophysical Research，105（B10）：23765-23789.

Lay T.2011.Earthquakes：a Chilean surprise.Nature，471（7337）：174-175.

Oglesby D D.2005.The dynamics of strike-slip step-overs with linking dip-slip faults.Bulletin of the Seismological Society of America，95（5）：1604-1622.

Ohnaka M，Yamashita T.1989.A cohesive zone model for dynamic shear faulting based on experimentally inferred constitutive relation and strong motion source parameters.Journal of Geophysical Research：Solid Earth（1978—2012），94（B4）：4089-4104.

Ohnaka M.1993.Critical size of the nucleation zone of earthquake rupture inferred from immediate foreshock activity.Journal of Physics of the Earth，41（1）：45-56.

Ohnaka M.1996.Nonuniformity of the constitutive law parameters for shear rupture and quasistatic nucleation to dynamic rupture：aphysical model of earthquake generation processes.Proceedings of the National Academy of Sciences of the United States of America，93（9）：3795-3802.

Ohnaka M，Shen L F.1999.Scaling of the shear rupture process from nucleation to dynamic propagation：Implications of geometric irregularity of the rupturing surfaces.Journal of Geophysical Research：Solid Earth（1978—2012），104（B1）：817-844.

Olsen-Kettle L，Weatherley D，Saez E，etal.2008.Analysis of slip-weakening frictional laws with static restrengthening and their implications on the scaling，asymmetry，and mode of dynamic rupture on homogeneous and bimaterial interfaces.Journal of Geophysical Research：Solid Earth（1978—2012），113（B8）.

Palmer A C，Rice J R.1973.The growth of slip surfaces in the progressive failure of over-consolidated clay.Proceedings of the Royal Society of London.A.Mathematical and Physical Sciences，332（1591）：527-548.

Rodgers D A，Balance P E，Reading H G.1980.Analysis of pullapart basin development produced by en echelon strike-slip faults.Sedimentation in Oblique-Slip Mobile Zones，Spec.Publ，4：27-41.

Rojas O，Day S，Castillo J，etal.2008.Modelling of rupture propagation using high-order mimetic finite differences.Geophysical Journal International，172（2）：631-650.

Ryan K.2012.Dynamic models of earthquake rupture on fault stepovers and dip-slip faults using various friction formulations［Ph.D.］.University of Californica.

Scholz C H.1998.Earthquakes and friction laws.Nature，391（6662）：37-42.

Scholz C H.2002.The Mechanics of Earthquakes and Faulting.Cambridge：Cambridge University Press.

Shen Z K，Sun J B，Zhang P Z，etal.2009.Slip maxima at fault junctions and rupturing of barriers during the 2008Wenchuan earthquake.Nature Geoscience，2（10）：718-724.

Shi Z Q，Ben-Zion Y，Needleman A.2008.Properties of dynamic rupture and energy partition in a solid with a frictional interface.Journal of the Mechanics and Physics of Solids，56（1）：5-24.

Shibazaki B.2005.Nucleation process with dilatant hardening on a fluid-infiltrated strike-slip fault model using a rate-and statedependent friction law.Journal of Geophysical Research：Solid Earth（1978—2012），110（B11308），doi：10.1029／2005JB003741.

Stein S，Okal E A.2011.The size of the 2011Tohoku earthquake need not have been a surprise.Eos，Transactions American Geophysical Union，92（27）：227-227.

Tse S T，Rice J R.1986.Crustal earthquake instability in relation to the depth variation of frictional slip properties.Journal of Geophysical Research：Solid Earth（1978—2012），91（B9）：9452-9472.

Wang X C.2003.Finite Element Method（in Chinese）.Beijing：Tsinghua University Press.

Wesnousky S G.2006.Predicting the endpoints of earthquake ruptures.Nature，444（7117）：358-360.

Xia K，Rosakis A J，Kanamori H，etal.2005.Laboratory earthquakes along inhomogeneous faults：Directionality and supershear.Science，308（5722）：681-684.

Yuan J，Zhu S B.2014.FEM simulation of the dynamic processes of fault spontaneous rupture.Chinese J.Geophys.（in Chinese），57（1）：138-156.

Zhang H M，Chen X F.2006a.Dynamic rupture on a planar fault in three-dimensional half space—I.Theory.Geophysical Journal International，164（3）：633-652.

Zhang H M，Chen X F.2006b.Dynamic rupture on a planar fault in three-dimensional half-space—II.Validations and numerical experiments.Geophysical Journal International，167（2）：917-932.

Zhu S B，Zhang P Z.2009.A study on the dynamical mechanisms of the Wenchuan Ms8.0earthquake，2008.Chinese J.Geophys.（in Chinese），52（2）：418-427.

Zhu S B，Zhang P Z.2013.FEM simulation of interseismic and coseismic deformation associated with the 2008Wenchuan Earthquake.Tectonophysics，584：64-80

Zienkiewicz O C，Taylor R L，Zhu J Z.2005.The Finite Element Method：Its Basis and Fundamentals：Its Basis and Fundamentals.Butterworth-Heinemann.

附中文参考文献

王勖成.2003.有限单元法.北京：清华大学出版社.

袁杰，朱守彪.断层自发破裂动力过程的有限单元法模拟研究.地球物理学报，2014，57（1）：138-156.

朱守彪，张培震.2009.2008年汶川Ms8.0地震发生过程的动力学机制研究.地球物理学报，52（2）：418-427.