跨孔雷达全波形反演成像方法的研究

吴俊军，刘四新，李彦鹏，张宇生，张丽丽，傅磊，王飞，孟旭，雷林林

1中国石油集团东方地球物理勘探有限责任公司新兴物探开发处，涿州 072751

2吉林大学 地球探测科学与技术学院，长春 130026

3沈阳航空航天大学 电子信息工程学院，沈阳 110034

1 引言

跨孔雷达全波形反演是一种使用全波形信息反演两钻孔之间地下信息的层析成像技术.在地震勘探中，全波形反演能够提供小于波长的分辨率，在理想状态下，分辨率能够达到1／2～1／3波长（Pratt，1999）.利用声波的全波形反演方法比利用射线方法在分辨率上能提高一个量级.探地雷达全波形反演的发展得益于其与地震学的高度相似性，以及近年来电磁学的快速发展.例如将麦克斯韦方程代替声波方程或弹性波方程，而解的形式与地震学非常相似，所以地震全波反演方法在过去三十年里所取得的发展，对跨孔雷达全波反演方法的研究起到了很大的促进作用.Johnson等（2005）以及 Cai等（1996）分别使用了菲涅尔量以及程函方程的方法进一步推动了波形反演技术的发展.许多探地雷达学者采用了修正的散射成像技术进行波形成像（Zhou and Liu，2000；Zhou et al.，2007；Cui et al.，2004）.Kuroda等（2005）和 Meles等（Meles et al.，2010；Meles et al.，2011；Meles et al.，2012）使用全波反演的方法对跨孔雷达数据成像，并取得较好的效果.Kuroda等的方法只考虑介电常数，而Ernst等（Ernst et al.，2007）通过级联更新的方法既考虑介电常数，又考虑电导率.后者的基本想法是固定电导率反演介电常数，反之亦然.两种方法的共同点在于其本质上都是标量的.Meles等提出的波形反演方法考虑电参数的矢量性，反演过程中允许介电常数和电导率同时更新.与常规射线追踪方法相比，全波反演方法能够更加有效的识别亚波长异常体.Belina等对不同随机模型下的全波反演子波估计进行了深入的研究（Belina et al.，2012a；Belina et al.，2012b；Belina et al.，2012c）.

本文全面推导了全波形跨孔雷达层析成像反演方法.通过基于局域网的分布式并行算法，有效地解决了巨型数据正演计算问题，从而实现了全波形跨孔层析成像方法在普通计算机上全面有效的运行.本文中首先建立了基于单轴各向异性介质完全匹配层（UPML）吸收边界的TE模式下的时间域有限差分 （FDTD）二 维 正 演 算 法 （Taflove Hagness，2005）.由于跨孔雷达测量方式中发射天线与接收天线极化方式为垂直于地表的z方向，因此选用FDTD正演算法时需要使用有Ex、Ez、及Hy的TE模式.反演算法采用最速梯度法求解，通过应用包括时间维度在内的全波场信息与残场逆向传播的全波场信息乘积来计算梯度方向，通过求取以步长为自变量的目标函数的极值确定步长公式.由于介电常数与电导率在量级上的区别，因此在确定迭代步长时需要对两种电性参数进行分别计算以提高收敛速度，这里需要分别使用不同的稳定因子.文中对介电常数及电导率分别采用对数化处理，并推导出新的梯度公式.采用参数对数化处理能够很好的提高收敛速度及稳定性，并且拓宽了异常与周边介质物性参数对比度.

在不降低分辨率的情况下，通过对反演模型采用抽稀的办法，将数据减小至原内存需求的1／6，以解决大型模型对计算机内存的巨大需求，文中分别对不同类型的模型进行了全波反演成像，取得了较好的结果.本文提出将第一步单介电常数反演作为初始模型（吴俊军，2012），有效的解决了同步反演收敛速度较慢的问题.

2 跨孔雷达全波反演理论推导

2.1 正演问题的积分表达形式

为了更好地全面表达波场情况，麦克斯韦方程可以表示成如下形式（Meles et al.，2010）：

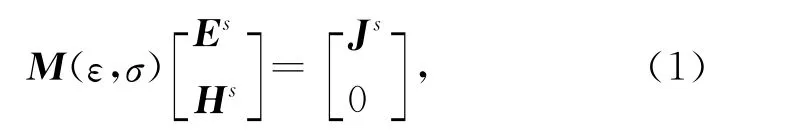
其中，Js为电流密度源，Es和Hs为产生的电场和磁场，上角标s表示指定的源，M（ε，σ）为一线性算子，在本文中由于未涉及到磁介质，因此本文中假定磁导率为常数，其值为μ0.M（ε，σ）代表麦克斯韦方程组，使得在任意点任意时刻方程组可以表示如下：

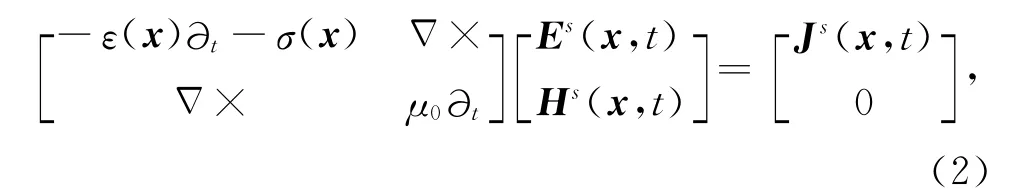
其中，ε（x）、σ（x）分别为空间变量x的介电常数和电导率分布.场量值是关于空间和时间的矢量，而电性参数仅是位置变量x的标量.向量Es和Hs不是特指某一时刻某一空间点的值，而是包括整个空间域和时间域的所有场值，即

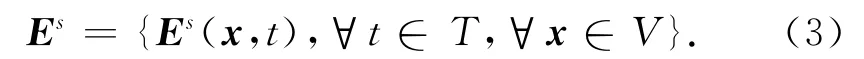
由于在以下的讨论中均只使用了电场值，因此省略Hs，得到一个简单的方程：

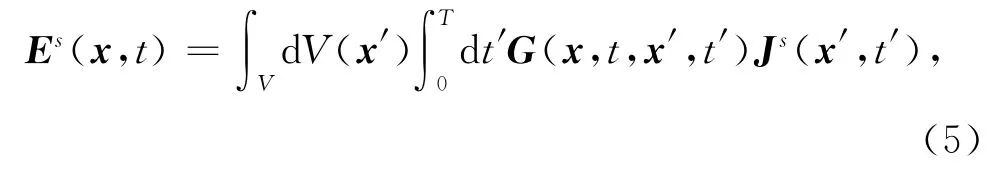
式中，Es（x，t）为源Js在 （x，t）产生的电场，G（x，t，x′，t′）为源Js（x′，t′）的格林函数张量.对于三维介质，可以用下角标的方式写出每个方向分量的电场：

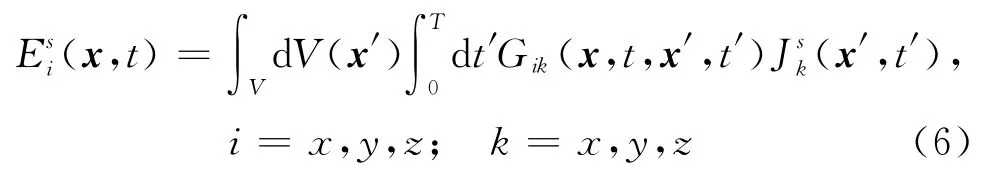
其中，Esi（x，t）为电场各个方向的分量，Gik（x，t，x′，t′）为格林函数张量各个方向的元素，Jsk（x′，t′）为源对应各个方向的分量.本文中使用向量的方式来表达方程，在使用中很容易就能转变为张量形式（Meles et al.，2010）.

2.2 目标函数方程的梯度计算

地球物理反演中有多种多样的反演问题（Greenhalgh et al.，2006）.全波形层析成像反演问题主要目的是寻找介电常数ε与电导率σ的空间分布.利用正演模拟数据道与实测数据道之差的平方最小准则来求解目标函数S（ε，σ）.目标函数可以写为

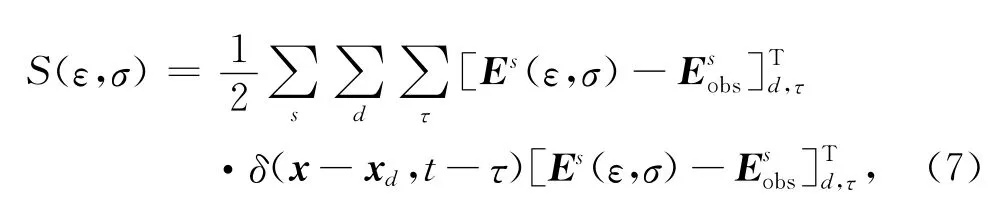
式中，Es（ε，σ）和分别为正演数据和观测数据，T为转置符号.（7）式分别在源s，接收点d以及观测时间τ三个方向上求和.误差方程的关键部分是电场求解，由于电场是关于介电常数和电导率的方程.要找到误差方程的梯度，需要对关于这些参数的电场进行一阶近似.与（1）式相似，可以写出扰动系统下的麦克斯韦方程组.

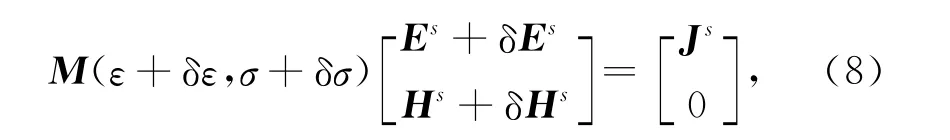
（8）式减去（1）式得

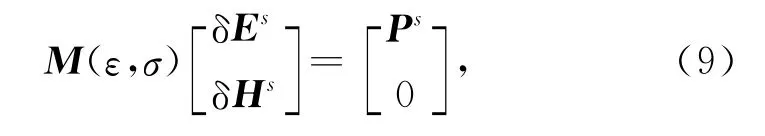
（9）式包含了与（1）式相同的算子M，此时作为源的这一项表示如下：

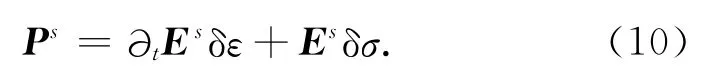
在空间域，这是一个关于扰动正演电场的方程.将（10）式代入到（4）式得到：

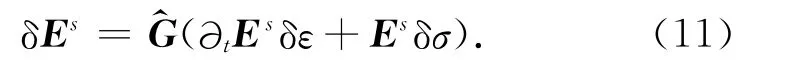
将（11）式展开得到：

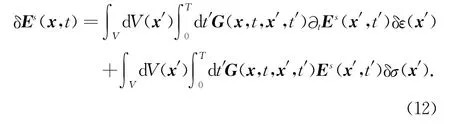
引入一个新核函数（或称敏感因子）Ls可以分别表示为如下：

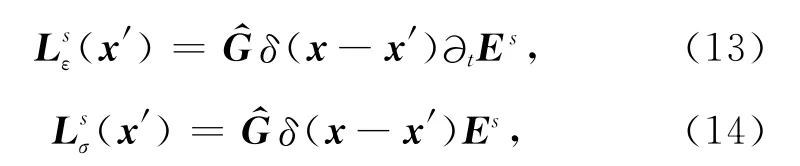
则其在任一点x，每个时刻t的展开式如下：

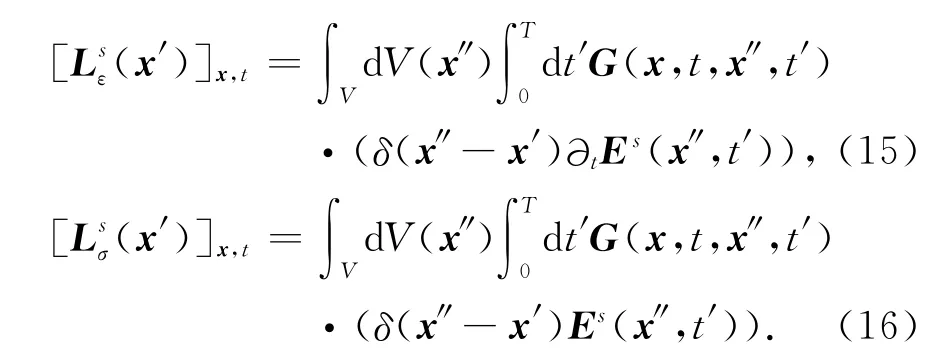
利用delta函数的积分性质得到：

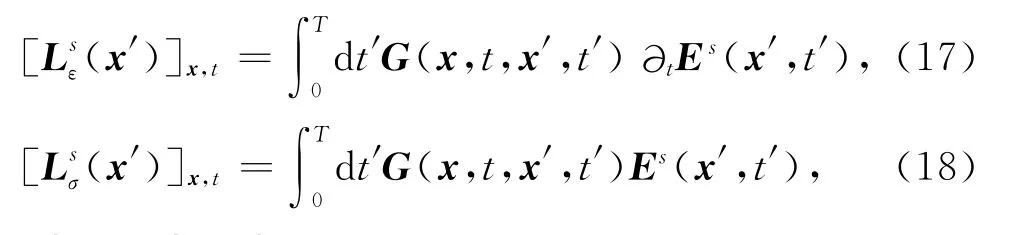
则（12）式可表示如下：

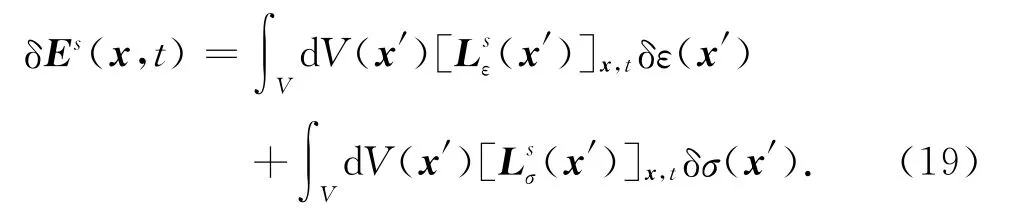
（11）式可表示为

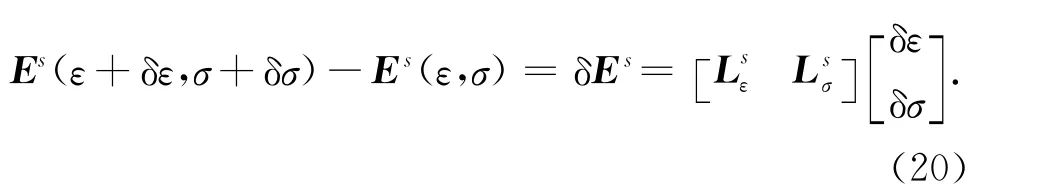
直接计算核函数Ls需要将每一个位置x′作为源都进行一次正演计算.但在本文的全波反演过程中，并没有直接使用敏感算子Ls，而是将它应用在残差的处理上，在下文中将会介绍，在残差计算时仅需解决一次正演问题.由于误差方程（7）式并没有考虑全部空间的波场（只考虑了接收点位置的正演数据与观测数据之差），在下文中，将使用算子Fs，该算子线性化描述所有接收点和观察时间的电场：

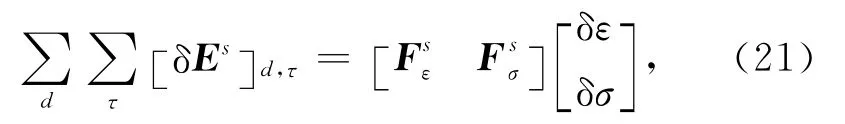
其中，

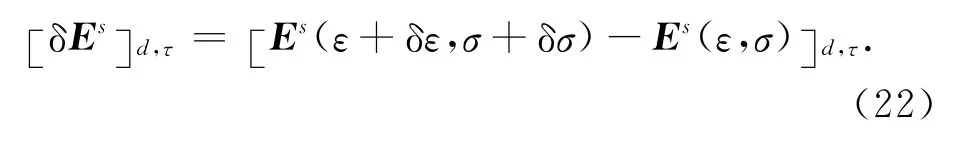
对于算子Fs，并不能像Ls那样简单定义.在下文中继续使用Ls代替Fs进行梯度计算.值得注意的是Fs区间是Ls区间的一个子集，因此，计算Fs区间上等同于et al.，2010）.

误差方程梯度的推导使用的是扰动目标函数的一阶近似.即

将扰动目标函数正常展开：

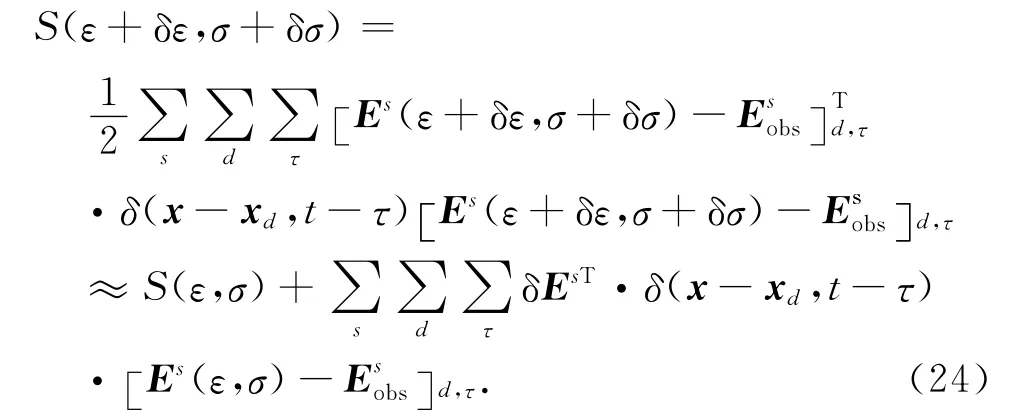
通过比较（23）式与（24）式，并对梯度使用与（21）式相同的线性化手段，很容易得到目标函数的梯度为

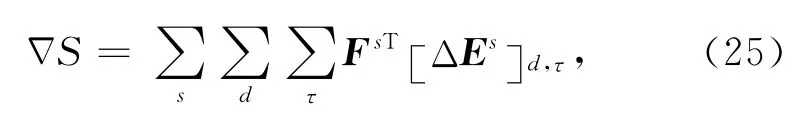
这里引进如下的接收点位置正演的电场与实测场的残场标记方法：

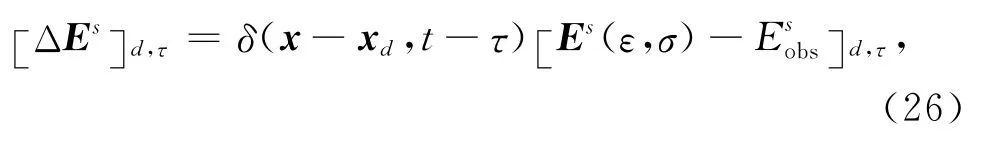
如2.1节所述的Fs及Ls的性质（即在接收点xd，接收时间为τ的Ls区间即为Fs的区间），得到：

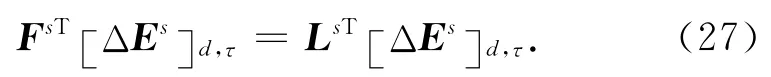
梯度找到后，将Ls的转置应用到残场.更确切的说，每一个元素（即每一个发射源、每一个接收位置、每一个接收时刻的全尺寸空间的介电常数或电导率）的梯度通过Ls与“残场源”［ΔEs］d，τ的内积获得.由于这个原因，本文之前推导了Ls详细的表达式.

总结（13）式及（14）式可以写出如下梯度式：

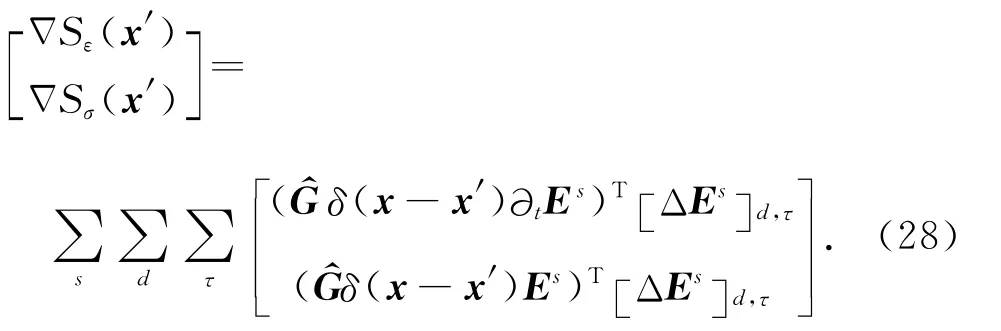
由于敏感因子Ls的计算需要正演，将Es项放在格林函数的左边，对“残场源”使用格林函数的转置.这样避免了直接对敏感因子Ls进行求解.上述提及的表达式很具有概括性，允许各种形式的数据反演（即允许任意的源和接收器的方向组合，也就是跨孔和井地测量（VRP））.

经过如上述变换，由（28）式可得

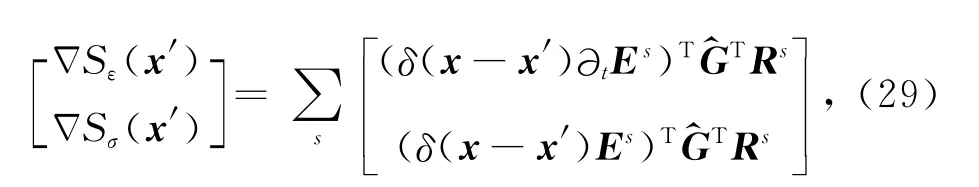
残差（“残场源”）之和Rs为：

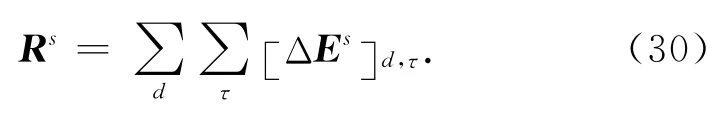
在（29）式中，Es表示在空间介质中麦克斯韦方程的电场解，而G＾TRs可以解释成在相同介质中后向传播的矢量场.（29）式简单的形式说明梯度是通过将所有源产生的所有时刻及空间三个维度（x，y，z）的场值与“残场源”产生相应时刻与空间场值的内积之和，该内积由前向传播向量场与后向传播残向量场相乘构成.该内积涉及整个时空域的Es、G＾TRs.对应的空间梯度分量由空间delta函数δ（x-x′）表示.

积分算子及其转置是通过其核函数的性质定义的，而线性算子及其转置拥有相同的核函数，唯一的区别为变量是积分还是相加（Tarantola，2005）.

在2.1节中，定义了算子G ＾对普通源Js的算法，为了给出GT清晰的说明，需要探讨G ＾的细节.对于源Js，接收点d，观测时间为τ，（6）式详细的给出了求解得到的电场的每个分量（i=x，y，z k=x，y，z）：

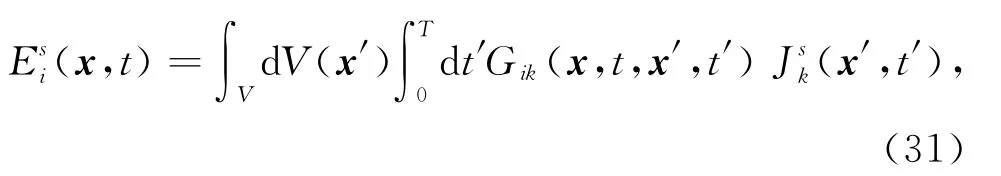
此时应当非常注意各个变量的位置以及格林函数、源和场的解对应的角标.算子G ＾=Gik（x，t，x′，t′）是全部空间V（x′）和时间域t′相加产生指定时空域电场Esi（x，t）的一个函数.而转置G ＾T=Gik（x′，t′，x，t）是指定时空域产生全部空间和时间域的函数.现定义一个新的矢量函数T，作为对残差（即“残场源”）［ΔEs］d，τ的作用：

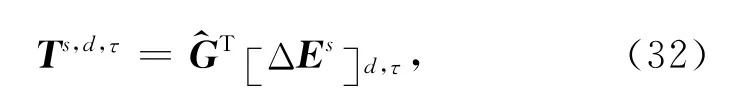
显示各个维度分量为

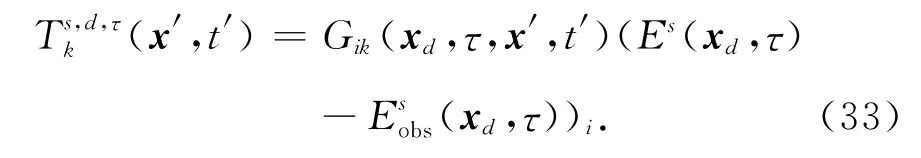
（33）式的形式与（31）不同，除了没有时间和空间的积分（我们考虑在时间域及空间域是一个delta函数，将这样一个积分作用到（33）式即与（31）式积分形式一致），格林函数的角标也与源（即“残场源”）的角标不同，时空的自变量也发生了变换.

为了更好的解释（33）式，这里使用互易定理（Harrington et al.，2001）：

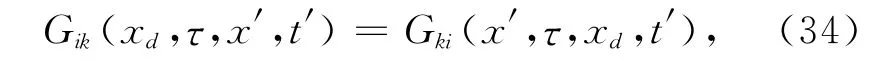
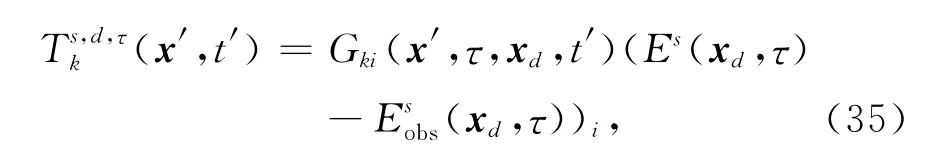
即格林函数下标变换的同时，函数变量表示空间位置的两元素变换位置，此时函数值不变.因此，重写（33）式，可得：这样就可以解释残差为什么可以作为一个源的传播问题.空 间 分 量（x′，t′）以及Gki张 量 与 向 量（Es（xd，τ）-（xd，τ））i的关系，就如（31）式中与源这一项关系一样.另外由于该问题具有时间的不变性，这意味着格林张量满足如下关系：

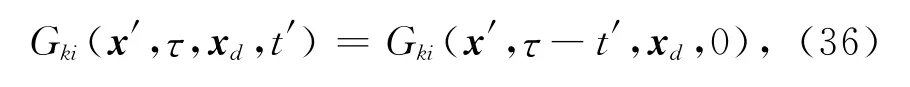
于是（35）式改写如下：

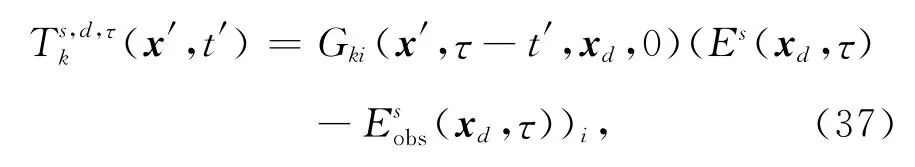
此时引入Ts，d，τ为三分量波场的矢量形式，可以将（29）改写为

将其展开，得到

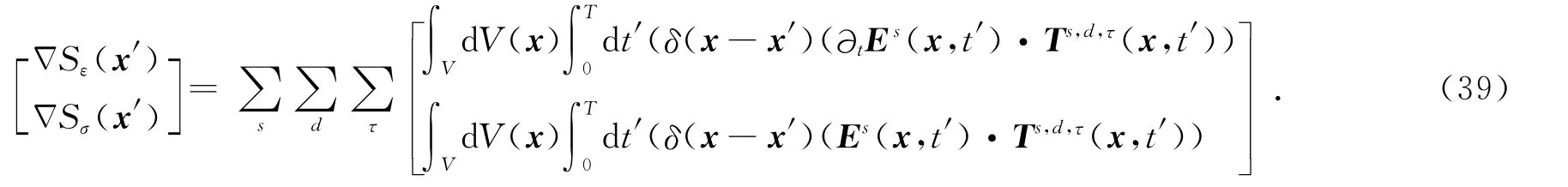
该等式可以理解为模型内任意点在时间域正向与反向传播矢量场零相位互相关，利用delta函数积分性质可得：Δ

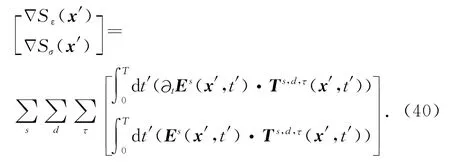
利用分布性质，可以将d和τ的求和移动到（40）式的积分里面，最后得到梯度的表达式：

Δ

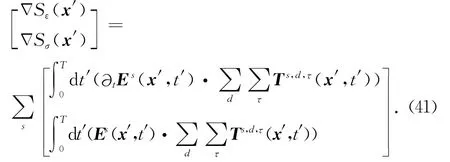
需要注意的是，此时“残差源”Ts，d，τ为多点源，即每一个接收点位置都有一个源，在时间上为逆时传播.

2.3 迭代步长的求解

一旦确定了梯度方向，下一步需要确定介电常数及电导率的迭代步长.理论上，介电常数和电导率迭代步长应遵循公式

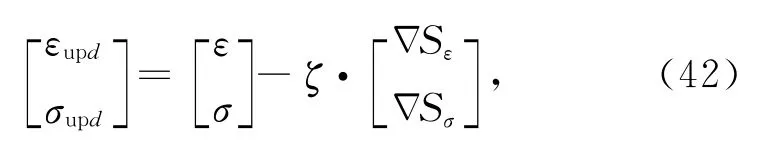
本文中使用最优化的方法能够找到迭代步长ζ（Pica et al.，1990），这里涉及到寻找一个沿负梯度方向的最小目标函数，即：

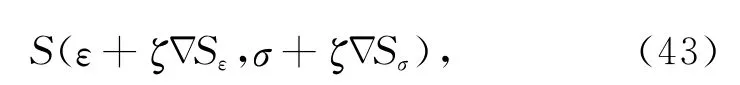
方程（43）中，当ε、σ、Sε、Sσ确定时只有唯一的独立变量（也就是迭代步长ζ），最小值通过目标函数一阶导数等于零很容易求得：

解（44）式可得（Pica et al.，1990）：

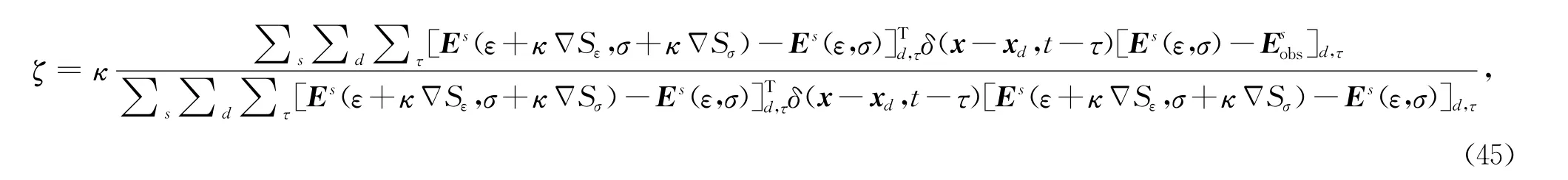
这里，Es（ε，σ）是模型参数 （ε，σ）的正演波场，κ是经验建立的扰动量（稳定因子），Es（ε+κΔSε，σ+κΔSσ）是计算介电常数及电导率在其各自的负梯度方向的正演电场（这个过程需要一个额外的时间域有限差分模拟（FDTD）），介电常数和电导率敏感度的巨大差异会导致复杂模型下同时反演的失败.Meles等（2010）通过建立一个特殊的模型，进行三次数值模拟实验量化这些差异，在同一模型下三种不同的扰动方式如下：

1.介电常数与电导率同时进行微扰Es（ε+κΔSε，σ+κΔSσ）-Es（ε，σ）；

2.纯电导率扰动Es（ε，σ+κΔSσ）-Es（ε，σ）；

3.纯介电常数扰动Es（ε+κΔSε，σ）-Es（ε，σ）.

试验说明仅使用电导率微扰的振幅非常小，与使用其他两种微扰方式存在两位数的差异，因此式（45）的步长求取方法主要取决于介电常数的梯度，而电导率的梯度基本不起作用.Ernst提供了一个级联方式反演（Ernst et al.，2007），该方法是对介电常数进行迭代反演时，保持电导率不变；类似的，对电导率进行反演时，保持介电常数不变.在介电常数反演中为了最小化电导率异常的影响，将模型每一道数据除以其振幅能量，使得残场数据归一化，而在电导率反演中则采用正常的残场数据.

相比之下，Tarantola（2005）建议对于不同类型的模型参数采用不同的迭代步长.对于GPR数据，迭代步长采用如下模式：

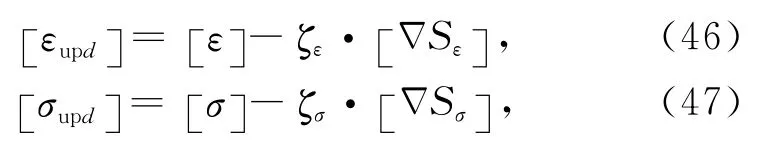
因此另外一种反演方法为一个介电常数和电导率在每一次迭代中的准同步反演，该方法通过各自沿ΔSε、ΔSσ方向寻找极值点，目标函数为

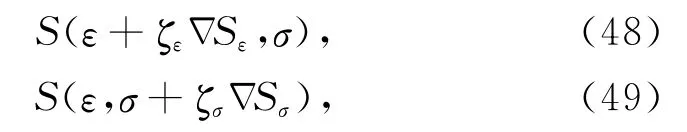
得到：

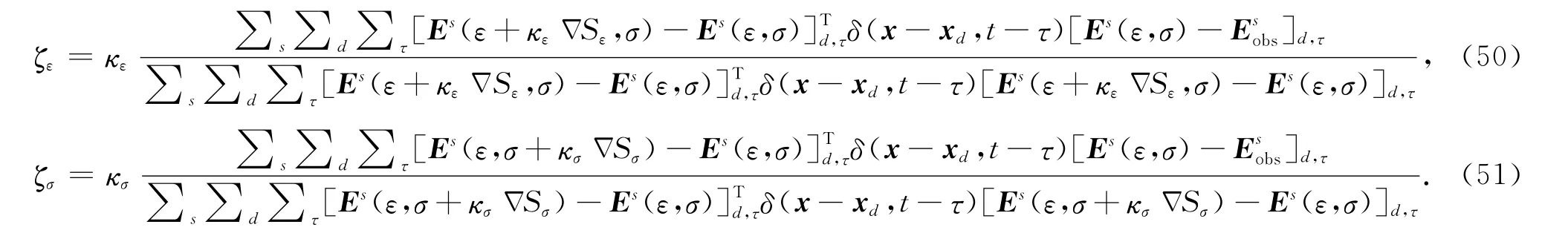
其中κε、κσ为不同的小稳定因子.对于小稳定因子κε、κσ要很小心的取其上下界限.这些稳定因子在反演中需要更新，在本文数值实验中，κε=10-9，κσ=105，尽管该方法需要一个额外的两次正演模型计算，但是同步反演过程的性质减少了所需FDTD的总数，因为在一次迭代中介电常数和电导率可以同时更新.本文全波反演过程在每个源位置每次迭代需要计算四次正问题：第一次计算正演数据，第二次计算梯度方向残差，另外两次计算迭代步长.与Ernst相比，其在一次正演模型中，并不能将介电常数和电导率同时算出，该方法共需6次正演计算.此外，采用级联方式，需要去选择变换介电常数和电导率时介电常数／电导率的迭代次数，而同步迭代则不需要，所以同步迭代实现起来更简单一些.流程图如图1所示，其中res-FDTD表示残场FDTD计算，add-FDTDε、add-FDTDσ分别表示计算介电常数和电导率迭代步长时额外的两次FDTD计算（Reiter and Rodi，1996）.

2.4 对数化物性参数

推导的反演算法是基于自然参数ε，σ和μ0的，但是不同的参数化形式让计算（也就是在模型空间中变换坐标）更容易实施.通常采用一种对数的表示方法：

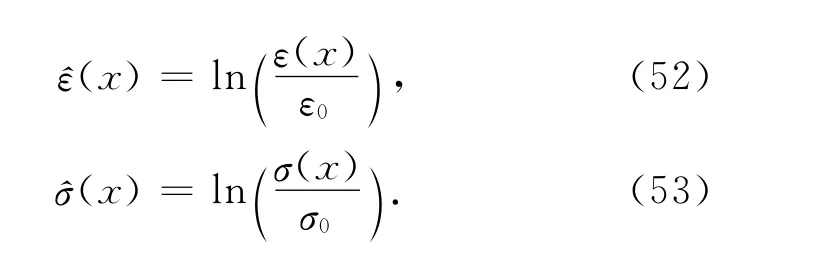
其中，ε0是真空中介电常数，σ0为任意的电导率，这里采用1S·m-1，因为模型空间为线性空间，使用对数化表示参数在反演中很重要（Tarantola，2005）.此外，该参数化能够确保介电常数和电导率为正值，且可以压缩模型的数值，使其可以适应更大的数值跨度（Ernst et al.，2007）.在反演中这样表达的变化仅仅影响到梯度方向的表达式.为求解新的梯度方程，首先引入一个新的目标函数表达式：

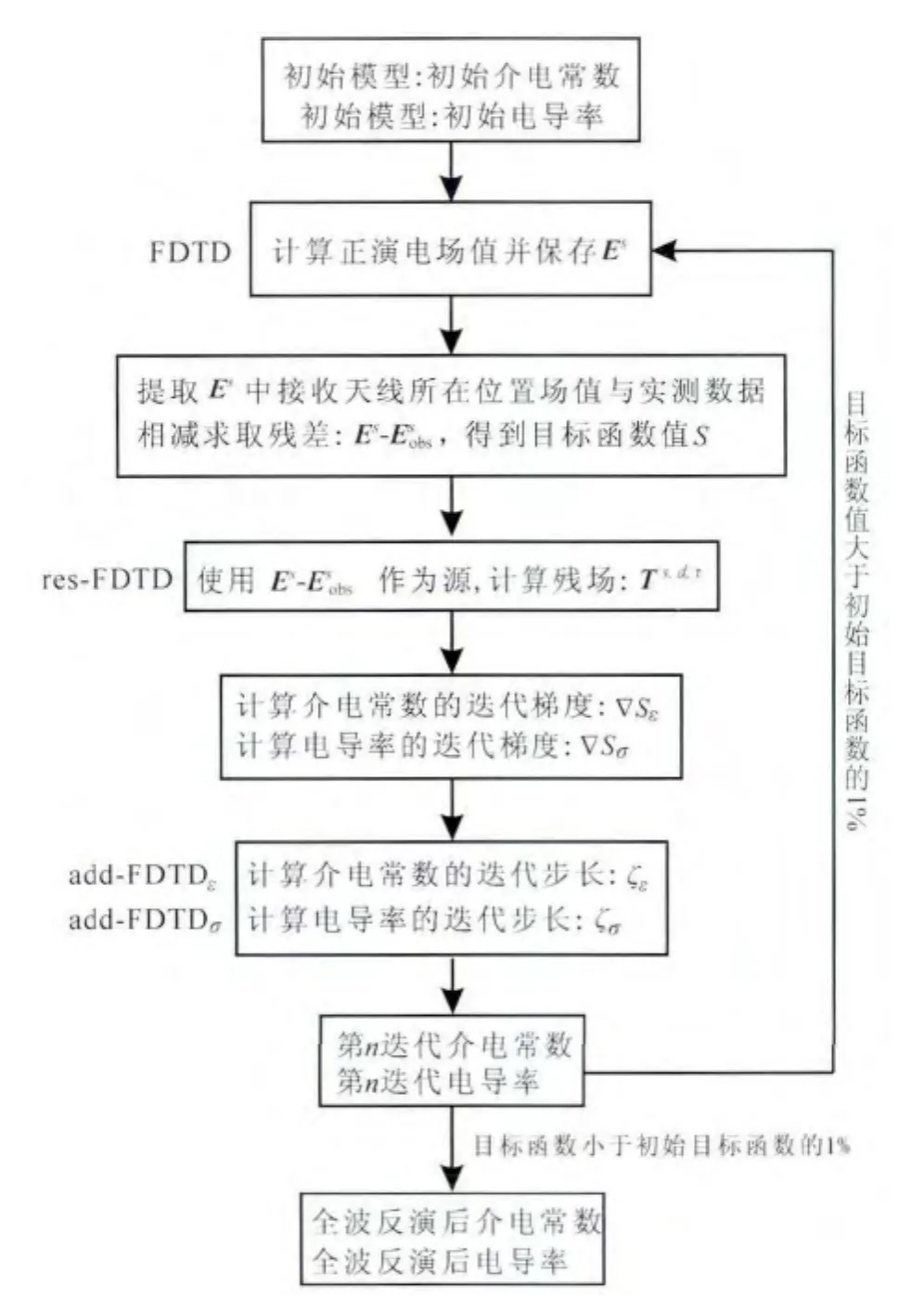
图1 跨孔雷达全波反演计算流程Fig.1 Flow chart of cross-hole GPR full-wave inversion

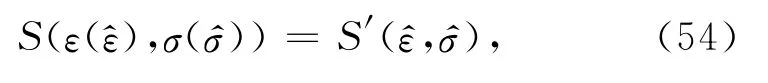
将新梯度函数S′ε＾，S′σ＾表示成Sε，Sσ的函数.表达式如下：

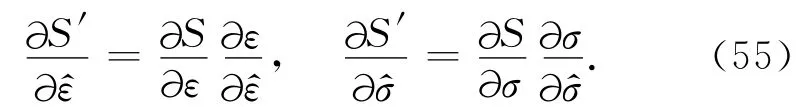
根据（52）、（53）式的定义，从（29）式可得：

Δ

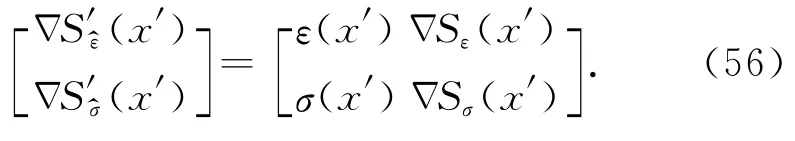
2.5 全波反演计算效率及分布式算法

MATLAB Distributed Computing Engine（MATLAB分布式计算引擎，MDCE）及Parallel Computing Toolbox可以开发运行基于机群系统的分布式及并行MATLAB算法，且无需改变原有的MATLAB科学计算开发环境（MathWork Product Documentation，2011）.

在2.2及2.3中提出了完整的求解介电常数及电导率全波反演的梯度和迭代步长算法，能够处理3D或者2D问题.然而，目前计算机在计算多个3D的FDTD正演时计算能力尚且严重不足，因此本文全波反演的反演算法是在直角坐标系的2D介质中.使用的是线源（在y方向上），即假设在y方向上介质参数及源没有变化，6个分量的EM场被分成两对独立的方程组（Taflove et al.，2005）.在跨孔雷达测量方式中仅需计算其中一组，即麦克斯韦方程组的TE模式（该模式电场分量始终与y向横切，与偶极天线匹配），这里存在三个分量：Ex，Ez，Hy.

为了在计算中确保稳定性和避免数值色散，需要考虑介质参数和源的频率组合.通常的要求是最短波长应大于10个网格长度（Taflove and Hagness，2005）.在本文的模型中，采用中心频率为100MHz的雷克子波，因此采用空间网格距离为5cm，这样每个模型有105～106个网格节点.根据发射天线到接收点的距离，需要几千个时间步长（为满足时间采样间隔的稳定性）去获得较长时间窗口的波场.由于采用UPML吸收边界，宽度上匹配层共占20层元胞.在计算迭代方向时，所有发射点产生的所有网格点的Ex，Ez场都需要保存在内存中，这需要产生大约40×NsrcGB内存，其中Nsrc为发射点的个数.由于模型空间的分辨率远小于正演模型网格离散度，采用抽稀的方法可有效降低内存需求.

Meles将3×3个正演元胞用一个反演元胞代替（Meles et al.，2010），在反演过程中并没有很明显的减小空间分辨率.本文中，对于不同的模型采用不同的抽稀模式，即对于跨孔测量，因其横向分辨率不如纵向分辨率，可选择在横向每隔2个节点取一个数，在纵向上尽量少抽稀，可以每隔一个节点保留一个电场值，在实际情况中这降低了大概一个量级的内存需求.在计算中应当尽量避免内存交换过程，提高单个机群节点的内存使用，保证计算机的正常运算.由于每个发射点位置的计算相互独立，计算程序可以在分布式计算机群上高效率的计算，该机群可以将每个发射点放置到一个CPU节点的核中.由于分派数据额外的传输时间消耗仅相当于一个正演过程的20%.因此，如果尽量避免数据通讯，完成一个完整的同步反演的计算时间Tcomp表示如下：

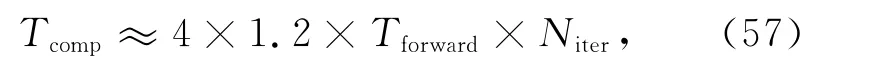
其中Tforward是单次正演计算所需要的时间，Niter为迭代的次数.

3 算例实现

3.1 小尺寸规则目标体成像

上文中已经系统的介绍了全波形反演层析成像技术的原理，下面首先以单介电常数反演为例，实现全波反演过程.模型1如图2所示为圆柱目标体模型，其在2D界面上为一个圆，围岩相对介电常数为εr=5.5、电导率为σ=0.0001S·m-1.目标体直径为1m，垂直方向位于深度3m的位置，水平方向位于3m的位置，目标体的介电常数为εr=7，电导率与围岩相同的，该目标体位于两个6m深的钻孔中间，两钻孔间距为6m.左边有13个发射装置，其间距为0.5m，用圆圈符号表示，在右边有13个接收装置，使用叉号表示.

从图2（b，c）可以看到已经对目标体区域进行了一个整体的勾勒，图2d为经过100次迭代后的全波形反演的图像（此时目标函数已远小于初始模型的目标函数（如图3a所示））.通过对比图2b以及图2d可以发现，全波反演成像分辨率得到了显著提高.图3b为第7个源第7接收器接收的第100次后子波与初始模型及实测模型的对比，可以看到经过迭代后的子波波形已经很好地与实测数据匹配.图3c为沿深度为3m的A-A（如图2a所示）所作切线，图3d为沿水平位置3m的B-B线（如图2a所示）所作的切线.图中，黑色曲线为理论曲线，蓝色曲线为经过一次迭代后曲线，红色曲线为经过100次迭代全波反演的波形图，可以看到经过反演后的结果与观测的子波匹配的很好.从图3（c，d）可以看出，在水平方向上，异常高值区域在图中跨度较大，可以看出跨孔方法在垂直方向上的分辨率要优于水平方向的分辨率.

3.2 大模型成像

模型2为如图4a所示，发射井与接收井深度均为20.5m，两井之间距离10m，目标体为矩形，其中心点位于垂直距离10m、水平距离5m的位置，该矩形区域为正方形，边长为2m，其介电常数为εr=7，电导率为σ=0.0001S·m-1.围岩介电常数为εr=5.5，电导率为σ=0.0001S·m-1.发射天线水平位置为0m，垂直位置从1m开始，到20.5m结束，共40个位置，间隔0.5m；接收天线水平位置位于10m，垂直位置从1m开始，到20.5m结束，同样共40个位置，间隔0.5m.

图4b为其全波反演结果，该图能够精确的反演出矩形目标体的形状及电性参数大小，并且非常精确的反演出矩形目标体的上下两条边，左右两条边也能够较准确的与模型对应.模型2使用了大尺寸区域参与计算，这对计算机硬件要求则提高到另外一个量级，以本模型为例，模型离散间隔为0.05m，网格数为240×480，FDTD时间迭代次数为1732次，共有40个源位置，同样采用单精度（4bit）保存，电场值保存需要内存240×480×1732×40×4／1024／1024／1024=29.7318G，计算残场同样需要内存29.7318G，共计59.4635G内存.使用基于MDCE的并行算法后，每个worker需要承担的内存为59.4635G／40=1.4866G，本机群中的两台搭载6核的PC，其每个核对应一个worker，因此这两台PC每台需要承担的内存为1.4866G×6=8.9196G，虽然这两台电脑物理内存为16G，但8.9196G对其来说也是一个较大的载荷.这里使用了抽稀的方法降低内存占用空间，由于刻画该矩形异常体需要的分辨率数远低于FDTD的网格数，因此可以将介电常数的网格数抽稀.由于跨孔测量方法在纵向分辨率上表现更为出色，因此在纵向上每隔1个点抽取一个相对介电常数值，而在横向上每隔两个点抽取一个相对介电常数值，如此网格数量上将减少到原来的1／6，即每台PC占用内存1.4866G，这将大大降低内存的占用.

图5给出了由第20个源（Depth：10.5m）发射，介电常数反演后所有接收器接收的波形与初始模型及实测模型的对比.从图中可以明显的看到两者之间的差别.图5b中能够看出反演后结果与实测数据重合的非常好.为了进一步观察残差，图5c中可以看到相比初始模型与实测数据的残差，反演后结果与实测数据残差几乎为零.

3.3 复杂及随机模型成像

为了更好的体现全波形层析成像的能力，建立如图6a所示的复杂模型3，发射井与接收井深度为20.5m，两井之间距离10m，异常体位置及形状，深蓝色表示介电常数为εr=5，淡蓝色表示介电常数为εr=5.5，绿色表示介电常数为εr=6，深红色表示介电常数为εr=7.所有异常体电导率均为σ=0.0001S·m-1.发射天线水平位置为0m，垂直位置从1m开始，到20.5m结束，共40个位置，间隔0.5m；接收天线水平位置位于10m，垂直位置从1m开始，到20.5m结束，同样共40个位置，间隔0.5m.

图6b为其反演结果，从上到下依次可得：首先垂直深度2m处可以清晰的分辨层状分界面，垂直深度6m附近的带状起伏薄层能够准确地反演出起伏的微观形态，能够清晰的分辨出垂直深度10m的长方形高值异常，对于14m深度附近水平倾角不是很大的倾斜异常，同样可以清晰的反演出结果.底部18m以下的垂直分界面，在垂直深度18m附近位置可以清晰的观察到其分界线，但越往深处，分界面逐渐被均质介质代替，原因为观测系统对该类别界面无法识别.

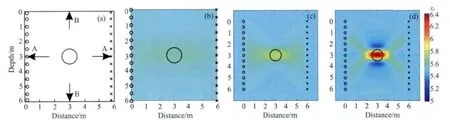
图2 （a）圆柱目标体示意图；（b）初至时射线追踪法反演结果；（c）第一次迭代后介电常数；（d）100次迭代后全波反演结果Fig.2 （a）Schematic diagram of cylinder body；（b）Inversion result of first-arrival ray method；（c）The permittivity after first iteration；（d）Inversion results after 100iterations

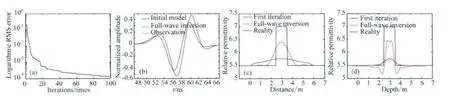
图3 （a）目标函数；（b）子波匹配情况；（c）深度3m介电常数切线（沿A-A所做切线）；（d）水平3m介电常数切线（沿B-B所做切线）Fig.3 （a）Objective function；（b）The wavelet matching conditions；（c）The permittivity in the depth of 3M （along A-A line）；（d）The permittivity in the distance of 3M （along B-B line）

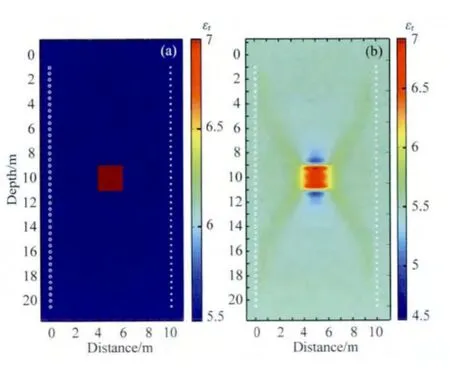
图4 矩形目标体（a）及其反演结果（b）Fig.4 The model（a）and inversion results（b）of rectangular object

随机模型（模型4）如图6c所示，该随机模型的水平相关长度为5m，垂直相关长度为1m.相对介电常数最小值4.8，最大值6.2.电导率值均为σ=0.0001S·m-1.发射天线水平位置为0m，垂直位置从1m开始，到20.5m结束，共40个位置，间隔0.5m；接收天线水平位置位于10m，垂直位置从1m开始，到20.5m结束，同样共40个位置，间隔0.5m.

从图6d反演结果中可以看出对于该尺寸相关长度的随机介质，本文的反演方法能够较清晰的分辨出0.5m以上的薄层.高介电常数值能够清晰看到的部分为（从上到下）：3.5m深度反演区域左侧的高值薄层、5m深度附近薄层、8m深度附近薄层、14m深度靠近发射源位置的高值区域，18m深度右侧部分.而14m右侧部分两个相连的更薄层则只能分辨出相对高值的一个.对于小于0.5m的微观结构，暂不能很好的区分开来.该反演结果能够很准确的完成层状结构划分的问题.

3.4 介电常数与电导率分别成像

模型5物性参数分别如图7（a，c）所示，发射天线（用圈形符号表示）位于水平距离0m位置，深度从0m到20.5m，共40个发射天线，间距为0.5m；接收天线（用叉形符号表示）位于水平距离10m位置，深度同样从0m到20.5m，共40个接收天线，间距为0.5m.

图5 第20个源（Depth：10.5m）发射，介电常数反演后所有接收器接收的波形与初始模型及实测模型的对比Fig.5 For（a）and（b），the transmitter located at position 10.5mdepth in Fig.4

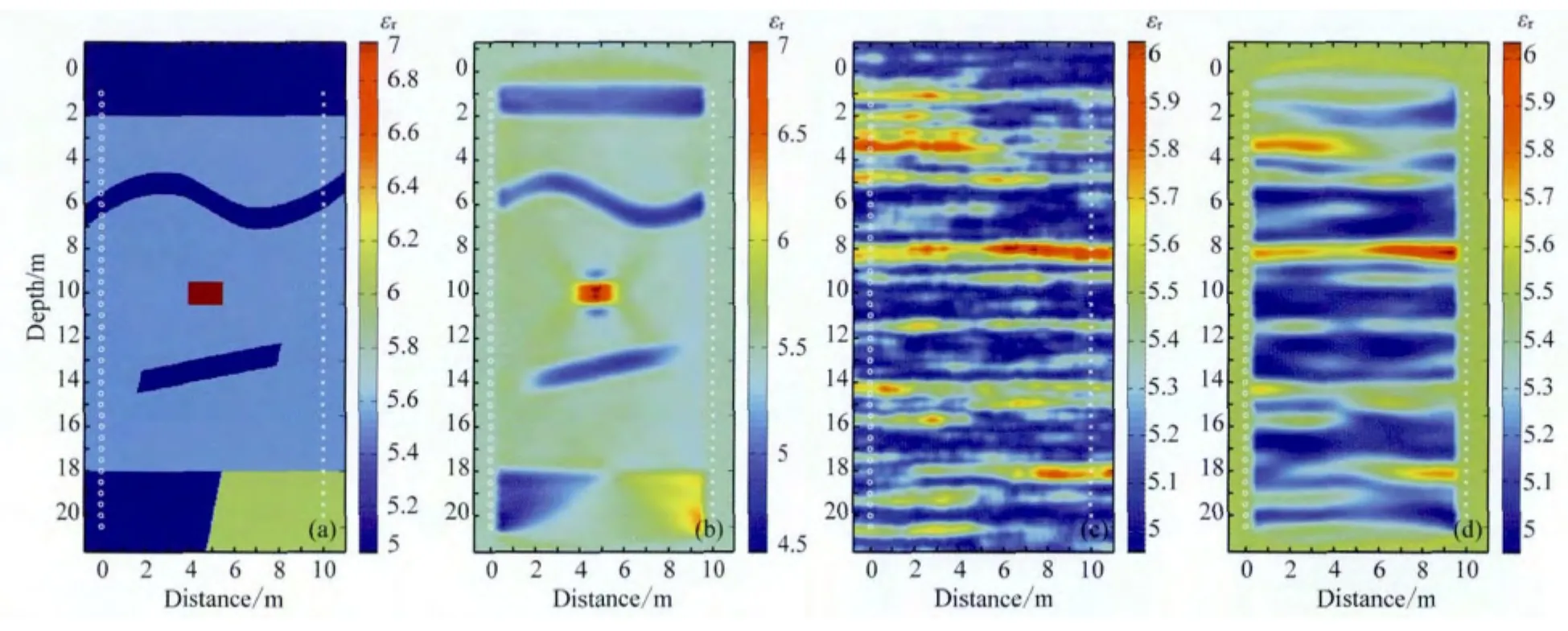
图6 （a）（b）复杂模型（模型3）及其反演结果；（c）（d）水平相关长度5m，垂直相关长度1m（模型4）及其反演结果Fig.6 （a）（b）Complex model（model 3）and its inversion results；（c）（d）Model of correlation lengths is 5mand 1m （model 4）in xand z directions and its inversion results

图7（b，d）分别为模型5的介电常数和电导率反演结果（均为10次反演迭代），介电常数反演结果能够清晰的分辨地层，以及大小尺寸的管线和空洞.而对于电导率反演从图中可以清晰的看出位于4m位置的水平界面以及位于16m附近的起伏地表，圆柱管线位置未能有效的区分开来，与介电常数反演相比，12.5m深度的空洞反演形状略有畸变.且在没有射线穿过0m以上和20.5m以下区域，也能够反演出结果.

3.5 介电常数与电导率同时成像

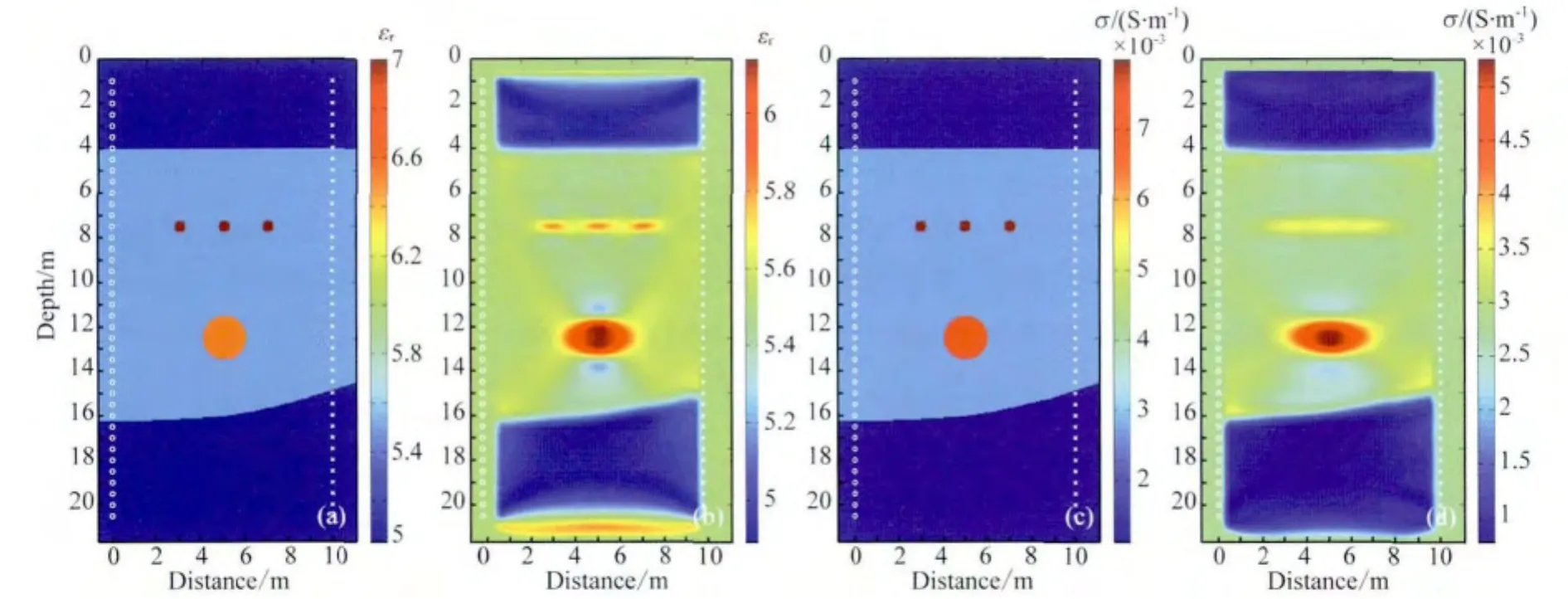
图7 大尺寸复杂模型（模型5）及介电常数与电导率分别反演结果Fig.7 Large-scale complex model（model 5）and the inversion results of permittivity and conductivity

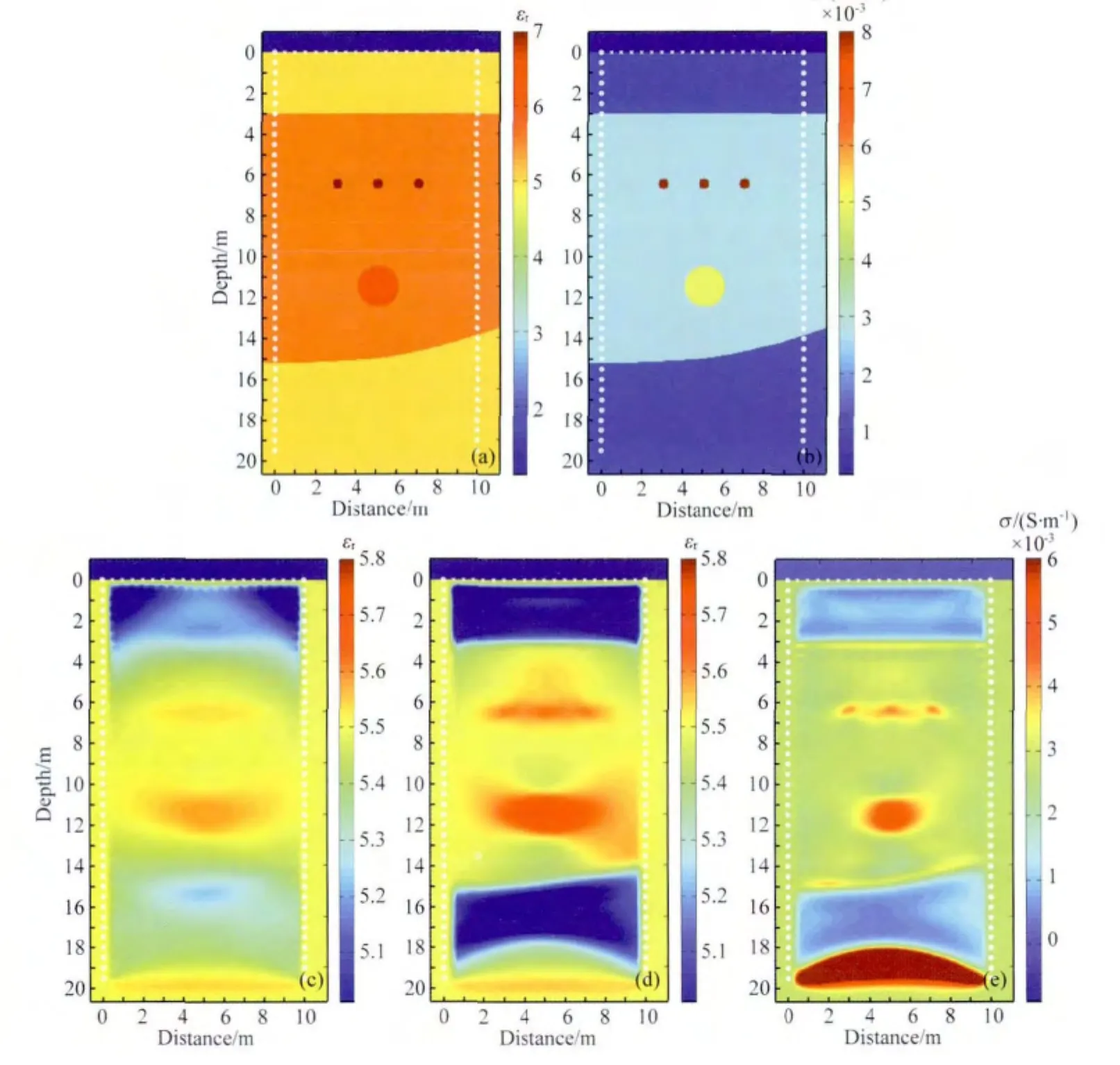
图8 结合VRP测量方式考虑地表的模型（模型6）Fig.8 The model combined with VRP measurement and considered the surface（model 6）

本节中，将对介电常数及电导率同时进行反演，并且加入了井地测量（VRP）测量系统.为了有效解决初始模型问题，本文提出采用第一次介电常数梯度作为同时反演成像的初始模型，能够有效提高收敛速度.图8中该模型共进行26次迭代将目标函数计算至初始目标函数的1%以下水平.从图中的介电常数和电导率反演结果可以看出，电导率的反演结果对管线的成像更清晰；加入VRP测量模式后，横向分辨率有所提高，但也造成了管线成像形状的畸变，同样观察11.6m深度的空洞成像，可看出其横向分辨率有较大的提高，但也发生了一定程度的畸变.在接近下底面的位置，电导率反演出现了很大的区域不收敛，相应的介电常数反演模型中同样存在这样的问题，在接近底部位置出现了较大的假高值区域.同样因为电导率的问题，造成了介电常数反演结果在底部出现了边缘效应.

反演结果可以看出电导率对管线和空洞的成像效果要好于介电常数成像.

4 结论

本文全面推导了全波形跨孔雷达层析成像反演方法，通过基于局域网的分布式并行算法，有效地解决了巨量数据的正演计算，将目前仅能在超级计算机上进行计算的全波形跨孔层析成像方法在普通计算机上全面有效的实现.正演中采用了基于UPML吸收边界的TE模式的二维FDTD算法.反演中通过应用包括时间维度的全波场信息与残场逆向传播的全波场信息乘积计算梯度方向，且通过求取以步长为自变量的目标函数的极值确定步长公式.文中对介电常数及电导率分别采用对数化处理，并推导出新的梯度公式.在不降低分辨率的情况下，通过对反演模型采用抽稀的办法，将数据减小至抽稀前内存需求的1／6，解决了大型模型对计算机内存的巨大需求.通过构建矩形目标体模型可以发现全波反演能够精确的反演出矩形目标体的棱边位置、电性参数等.通过建立水平相关长度及垂直相关长度各异的随机介质模型可以发现，在100MHz天线频率下，介质介电常数3～8之间时，能够清晰的分辨出0.5m以上的水平薄层异常体.在介电常数及电导率同步反演中，本文提出将第一步单介电常数反演作为初始模型，有效地解决了同步反演收敛速度较慢的问题.

Belina F A，Irving J，Ernst J，et al.2012a.Evaluation of the reconstruction limits of a frequency-independent crosshole georadar waveform inversion scheme in the presence of dispersion.Journal of Applied Geophysics，78：9-19.

Belina F A，Irving J，Ernst J，et al.2012b.Analysis of an iterative deconvolution approach for estimating the source wavelet during waveform inversion of crosshole georadar data.Journal of Applied Geophysics，78：20-30.

Belina F A，Irving J，Ernst J，et al.2012c.Waveform inversion of crosshole georadar data：influence of source wavelet variability and the suitability of a single wavelet assumption.IEEE Transactions on Geoscience and Remote Sensing，50（11）：4610-4625.

Cai W Y，Qin F H，Schuster G T.1996.Electromagnetic velocity inversion using 2-D Maxwell′s equations.Geophysics，61（4）：1007-1021.

Cui T J，Qin Y，Wang G L，et al.2004.Low-frequency detection of two-dimensional buried objects using high-order extended born approximations.Inverse Problem，20（6）：S41-S62.

Ernst J R，Maurer H，Green A G，et al.2007.Full-waveform inversion of crosshole radar data based on 2-D finite-difference time-domain solutions of maxwell′s equations.IEEE Transactions on Geoscience and Remote Sensing，45（9）：2807-2828.

Greenhalgh S A，Bing Z，Green A.2006.Solutions algorithms and inter-relations for local minimization search geophysical inversion.Journal of Geophysics and Engineering，3（2）：101-113.

Harrington R F.2001.Time-Harmonic Electromagnetic Fields.New York：Wiley，IEEE Press.

Johnson T C，Routh P S，Knoll M D.2005.Fresnel volume georadar attenuation-difference tomography.Geophys.J.Int.，162（1）：9-24.

Kuroda S，Takeuchi M，Kim H J.2005.Full waveform inversion algorithm for interpreting cross-borehole GPR data.∥Proc.SEG Int.Expo.And 75th Annu.Meeting.Houston，TX，1176-1179.

Pratt R G.1999.Seismic waveform inversion in the frequency domain，part 1：Theory and verification in a physical scale model.Geophysics，64（3）：888-901.

MathWorks-Product Documentation.2011.Accelerating the pace of engineering and science.http：∥ www.mathworks.cn／help／techdoc／ref／f16-6011.html.

Meles G A，Greenhalgh S A，Green A G，et al.2012.GPR Full-Waveform sensitivity and resolution analysis using an FDTD adjoint method.IEEE Transactions on Geoscience and Remote Sensing，50（5）：1881-1896.

Meles G A，Greenhalgh S A，Kruk J V D，et al.2011.Taming the non-linearity problem in GPR full-waveform inversion for high contrast media.Journal of Applied Geophysics，73（2）：174-186.

Meles G A，Kruk J V D，Stewart A，et al.2010.A new vector waveform inversion algorithm for simultaneous updating of conductivity and permittivity parameters from combination crosshole／borehole-to-surface GPR data.IEEETransactionson GeoscienceandRemoteSensing，48（9）：3391-3407.

Pica A，Diet J P，Tarantola A.1990.Nonlinear inversion of seismic reflection data in a laterally invariant medium.Geophysics，55（3）：284-292.

Reiter D T，Rodi W.1996.Nonlinear waveform tomography applied to Crosshole seismic data.Geophysics，61（3）：902-913.

Tarantola A.2005.Inverse Problem Theory and Methods for Model Parameter Estimation.Philadelphia，PA：Soc.Ind.and Appl.Math.

Taflove A，Hagness S C.2005.Computational Electrodynamics：The Finite-Difference Time-Domain Method.3rd ed.Norwood，MA：Artech House.

Wu J J.2012.Research on cross-hole radar tomography using fullwaveform inversion method［Ph.D.thesis］.Changchun：Jilin University.

Zhou C G，Liu L B.2000.Radar-diffraction tomography using the modified quasi-linear approximation.IEEE Transactions on Geoscience and Remote Sensing，38（1）：404-415.

Zhou H，Sato M，Takenaka T，et al.2007.Reconstruction from antenna transformed radar data using a time-domain reconstruction method.IEEE Transactions on Geoscience and Remote Sensing，45（3）：689-696.

附中文参考文献

吴俊军.2012.跨孔雷达全波形层析成像反演方法的研究［博士论文］.长春：吉林大学.