黏声介质平面波有限差分叠前深度偏移及在莺歌海盆地的应用

李添才，谢玉洪，李列，王华忠，王新领，但志伟，胡江涛

1吉林大学地球探测科学与技术学院，长春 130026

2中海油能源发展股份有限公司工程技术物探技术研究所，广东湛江 524057

3

中海油湛江分公司，广东湛江 524057

4同济大学海洋与地球科学学院，上海 200092

1 引言

在莺歌海勘探区块内，底劈等现象导致的地层气上溢形成成像模糊带.其中原因既包括气体充填砂岩层导致波阻抗差变小，也存在气体充溢地层中导致的强吸收衰减.前者需进行多波勘探解决；后者需考虑用各种方法来补偿含气地层对地震波的吸收衰减效应.

目前，最常用的地震波吸收衰减补偿方法有Q反褶积方法和黏声介质叠前深度偏移方法.前者是针对零偏移距地震道（或叠后数据）进行的，后者是针对Q值空变且沿波传播路径进行吸收衰减补偿的.

反褶积是常规地震数据处理中提高地震记录分辨率的常用方法.最佳维纳滤波是常规的反褶积方法，是在最小平方意义下求最优解.但是，它是基于时不变理论假设进行的.地震波在地下介质传播时，其子波波形是时变的.在吸收衰减严重的地区，一般的维纳反褶积方法很难取得理想的效果.目前尚没有一个完善的理论来精确描述地下介质对地震波的吸收衰减作用.Futterman（1962）提出了基于线性吸收理论的常数Q介质模型.Kjartansson（1979）引入了与频率相关的复模量，对地震波线性吸收模型进行了完善.在这种模型中，吸收与频率的某一函数次幂成比例关系，较好地体现了地震波吸收与衰减过程中的因果性原则.Wang（2002，2008）通过子波数值试验对地震波衰减和反Q滤波补偿问题进行了研究，并用VSP下行波场得出的Q值作用于地表数据以提高分辨率.Chopra（2003）提出高频恢复（HFR）方法，使用 Wiener整形滤波器，从VSP记录求取描述地层吸收效应的反滤波算子，将其作用于叠加数据以提高叠加剖面的分辨率.Van der Baan（2012）提出的时变 Wiener滤波也可以实现与反Q滤波一样的吸收衰减补偿效果.任浩然等（2007）提出了在CMP道集中沿均方根速度定义的射线路径进行Q补偿的方法，改进了对零偏移距地震道进行Q补偿的不足.单道反Q滤波有其简单，改善处理后的子波特性等优点.但是，地震波的吸收衰减是沿着传播路径进行的，因此更好的补偿方法是基于黏声介质（甚至黏弹介质）中的叠前深度偏移方法.

Mittet等（1995）提出在频率空间域利用MeClellan变换进行黏声介质中的叠前深度偏移.用MeClellan变换进行黏声介质中的叠前深度偏移使得计算量变大.事实上，频率空间域的三维有限差分法是更为高效和精确的算法.螺旋坐标系下的三维有限差分方程求解更进一步加快了计算的效率.Wang等（2004）实现了单炮道集的黏声介质叠前深度偏移成像.

针对莺歌海探区的实际情况，本文提出黏声介质平面波有限差分法叠前深度偏移成像方法.黏声介质成像目的是补偿地震波的吸收衰减；采用平面波偏移方式是为了适应海上单炮数量巨大，提高波动方程偏移效率；有限差分法偏移是为了适应气云区域内外Q值的空间变化剧烈.在莺歌海某探区的实际数据上的叠前深度偏移试验表明，本方法是改善模糊区成像质量的一种较为有效的途径.

2 莺歌海探区地震成像模糊区的地震地质认识

莺歌海地区油气地震勘探遇到的首要问题就是模糊区成像问题.出现模糊区的原因应该从该区地质问题中进行分析.模糊区域大多出现在天然气上溢充填上覆地层的区域.通常该区域的含气层密度小、成岩差，而上覆地层密度大、成岩较好.由于重力作用和高温高压作用，上覆地层向下运移，气层透过裂隙向上运移.这种相互渗透作用的结果是上覆地层中由于气体充溢导致纵波速度变小、密度变小、波阻抗变小.由于噪音水平是不变的，而信号强度变弱（波阻抗变弱），这就导致该区成像剖面上信噪比通常较低.同时，由于气层通常为强的非弹性吸收衰减层，地震波在穿过该区域时能量被严重衰减，这同样导致了成像剖面上目标层能量非常弱.因此，在成像过程中最好能够考虑地震波的吸收衰减补偿.

上面分析的主要是地质因素所造成的成像问题，为了更好地进行成像，从成像技术本身也需要寻找原因.影响成像质量的三大要素为：数据、参数（速度，各向异性及品质因子等）和偏移算法.理想的数据应该是均匀覆盖的全方位高密度无假频的地震数据，通常海上数据无法满足上述要求，那么只能通过数据规则化来尽量得到一个合适的数据.参数的合理性是影响成像的核心问题，而参数重要性的主次可以分为速度、各向异性及品质因子.速度和各向异性因子主要影响地震波的走时，走时正确才能实现同相轴的同相叠加.而品质因子则主要影响地震波的振幅和地震子波的形态，利用品质因子进行的吸收衰减补偿可以改善介质非弹性吸收衰减带来的振幅和相位畸变问题.

该区域的沉积是比较稳定的，后期构造改造作用并不强烈，因此构造以平缓的反射层为主.由于气层穿透上覆地层，导致上覆地层速度降低是普遍的现象.但是气体穿透区域通常较小，这就表明即使同一套地层由于气层的穿透也存在强的速度变化和Q值的空间变化.另一方面，多方位窄缆观测或宽方位观测有利于改善模糊区的成像.同时，稳定的沉积层有利于通过横向对比建立比较好的偏移速度场，减弱模糊区内地震数据信噪比低带来的偏移速度估计的难度.由于穿透区域存在较多的裂隙作为气的通道，因此存在裂隙诱导的各向异性，偏移算法的选择方面需要考虑上述因素.能同时适应横向变速、（至少）VTI介质和吸收衰减情形的、高效率的成像方法是该区成像方法的基本选择.

3 地震波吸收衰减机制

目前使用的描述波传播的声波方程和弹性波方程都假定地震波在绝热介质中传播.即，波动一旦由某个特定震源产生，便将无限地延续下去.因此，随着波从震源区向外扩散，波动可以在空间上衰减，但质点运动的总能量却保持为常数.

地震波在真实介质中的传播与其在上述理想介质中的传播有很大不同.此时，地震波振幅会有除几何扩散因素之外的衰减，还会伴随着色散（即频散）现象的发生，造成频谱成分的改变，使地震波波形发生改变.真实介质中地震波的这种吸收与色散特性是与岩层的物质组成、饱和度、孔隙率等物理条件密切相关的，这种吸收与衰减的总体效应可以通过无量纲量——介质的品质因子Q来描述.其定义如下：

其中E是原波动体系内积存的总能量；ΔE是每个周期内因介质的非完全弹性因素而造成的能量损耗.

然而，上述定义对计算没有多大用处.实际应用中，我们常观测：（1）在固定波数的驻波中振幅随时间的变化；（2）在固定频率的行波中振幅随空间的衰减.

大量实际资料证明，真实介质对地震波的这种吸收是符合线性吸收机制的.也就是说，波可以分解成它的Fourier分量，每个分量可用（1）或（2）定义的方式进行研究，而随后的Fourier分量合成，给出衰减对实际地震信号的正确影响.

在（1）或（2）定义的观测情况下，对于具有线性应力-应变关系的介质，波振幅A与成比例.因此，（1）式可改写为

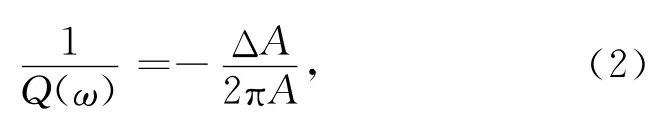
（2）式的解为

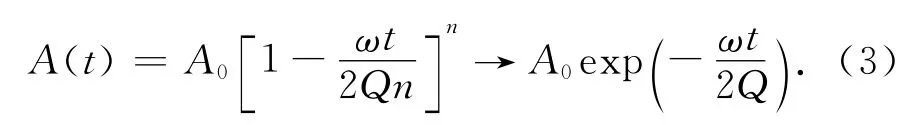
据此，可根据对指数衰减的振幅A（t）的观测来定义时间域的品质因子Q值.

同样地，其指数衰减的解为：

据此，可根据对指数衰减的振幅A（x）的观测来定义空间域的品质因子Q值.

应注意，为求衰减对一个波动解的影响，时间域中Q值对波传播的影响可看作是用复角频率代替实角频率ω；空间域中Q值对波传播的影响可看作是用复波数代替实波数k.在第一种情况下，要求复角频率ω有虚部在第二种情况下，要求复波数k有虚部

由于真实介质的复杂性，真实介质的黏滞特性表现出来的对地震波的吸收与衰减效应很难用一个数学物理模型来描述.Ursin（CWP408）对比了八种不同的描述地震波吸收衰减效应的数学模型.譬如K-F模型和K-J模型.对八种模型进行了归类.指出K-F模型和K-J模型的吸收衰减和频散曲线是非常类似的，可以归为一类.这两种模型在勘探地震学的吸收衰减补偿中是最常用的.

K-J模型（或Kjartansson模型）的数学表达式为（Kjartansson，1977）：

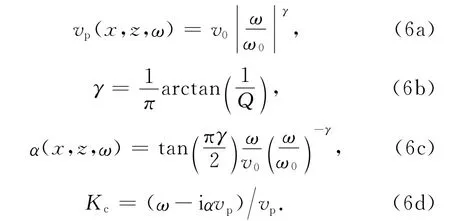
其中，v0代表参考速度，一般取声波速度；ω0表示参考频率，一般取为主频；v代表与频率相关的相速度；α为振幅衰减因子；γ为损耗角.

可见，若已知品质因子Q的分布情况（多设为水平层状模型），则可以给出（6d）式定义的复波数，地震波在空间中传播的吸收衰减情况可以得到描述.

吸收衰减介质中的波传播是不可逆的.表现在数学模型中就是吸收衰减补偿的结果是不唯一的.这种观点很多文献上都提及过.目前用K-J模型进行的吸收衰减补偿是勘探地震中常用的.它的效果是明显的.但是，没有严格的数学物理定理保证吸收衰减补偿的绝对合理性.一般地，还是用反Q滤波的效果、吸收衰减补偿PSDM效果来判断吸收衰减补偿是否合适.所做的基于K-J模型的很多数值试验说明了当Q值不是很小（小于15），正传播和补偿结果基本一致.但这只是基于K-J模型的很多数值试验，与实际问题存在差异.

另外，需要说明的是散射体引起的地震波散射现象也会改变观测到的地震波的振幅衰减与相位改变.Doherty和Anstey（1971）指出地震波穿过细层叠合地层时会发生地层滤波作用，导致地震波的振幅发生衰减，相位发生变化，而且它们是随偏移距不同而不同的.

但是，这两种现象引起的地震波振幅衰减和相位改变是很难区分的.因此，实际上我们用地震波振幅衰减估计出的Q值应该是两种效应的等效Q值.

4 平面波叠前深度偏移

4.1 平面波分解

采用平面波偏移的方式是出于计算效率的考虑，因为海上数据的单炮道集数量巨大.平面波偏移本质上是对炮道集进行线性编码（Hu et al.，2011），产生平面波数据.

震源平面波合成的公式可以表示为

其中，U（sx，sy；x，y；z=0；ω）代表炮点处的波场，（sx，sy）为炮点坐标；Up（psx，psy；x，y；z=0；ω）为合成出的震源平面波场.（psx，psy）代表震源波场的射线参数.同样地，可以合成出接收的平面波场.

由（7）式可以看出，平面波偏移过程是利用所有炮集数据合成由射线参数规定的不同方向的平面波数据，然后对这些平面波场进行叠前深度偏移.平面波数据的数目由射线参数 （px，py）的个数决定.这样平面波偏移的计算效率可以表示为单个平面波场数据偏移的时间乘以平面波数据的数目.而普通单炮道集偏移的计算效率为单炮道集偏移时间乘以单炮数量.海上观测通常有海量的单炮道集，采用平面波编码后合成平面波炮集的数量较少，这将会大大提高偏移的效率.Hu等（2011）详细讨论了利用编码技术进行多炮道集同时偏移的方法技术；Feng等（2009）讨论了如何得到更高质量的平面波数据.

4.2 平面波叠前深度偏移

从偏移成像过程看，单炮道集的叠前深度偏移和合成平面波炮集的叠前深度偏移是完全一样的，不同之处在于输入数据.合成平面波炮集的偏移也涉及到炮点波场外推和检波点波场外推，然后进行两外推波场的相关得到成像结果.炮点波场外推部分的输入为平面波震源（人为定义平面波源是非常简单的，与（7）式相同）；检波点波场外推部分的输入为合成的平面波数据（由（7）式定义）.波场外推后的成像条件依然是下行波场与上行波场在成像点处进行相关.由于射线参数规定了平面波方向，射线参数是已知的，因此生成射线参数道集是非常简单的，射线参数道集类似于某种角度道集.由于射线参数与入射角度之间受速度的影响，该道集不完全等价于角度道集.在用射线参数道集进行剩余速度估计时，需注意此差别.射线参数道集有特定的剩余速度估计公式.Stoffa等（2006）对平面波深度偏移有全面的总结.此处我们简单列出平面波叠前深度偏移的几个核心公式.

震源波场外推可以表示为

其中，w+［px，py；x，y，z；ω；v（x，y，z）］ 为某一类波场外推算子.本文中我们用单向波沿深度外推.USP（px，py；x，y，z；ω）为炮点平面波场.（px，py）规定平面波方向，（x，y）规定横向展布范围，z代表某一深度上的波场.ω为角频率.

检波点处波场外推公式为

公式中各量的含义与（8a）式类似，不再赘述.沿深度外推后的成像公式为

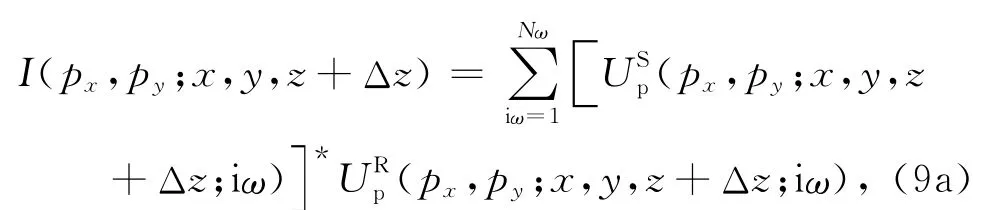
其中，I（px，py；x，y，z+Δz）为未叠加的成像结果.（9a）式右端项对频率成分的求和可以仅对正频率进行.

成像道集的形成可以写成

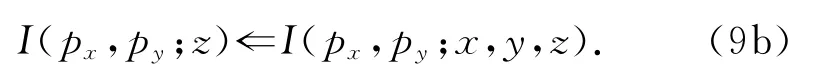
（9b）式为方位射线参数道集.实际情况下，我们仅仅沿某一方位角输出成像道集，譬如沿in-line方向形成成像道集.本文中的成像道集就是该式定义的，它是射线参数标示的道集，用来进行偏移速度分析.

5 黏声介质中有限差分法平面波叠前深度偏移算法

本文的核心思想在于在波传播过程中对介质的非弹性吸收衰减现象进行补偿，因此首先引出黏声介质中的波场外推方程.

声介质中单向波外推方程在频率空间域的表达形式如下：

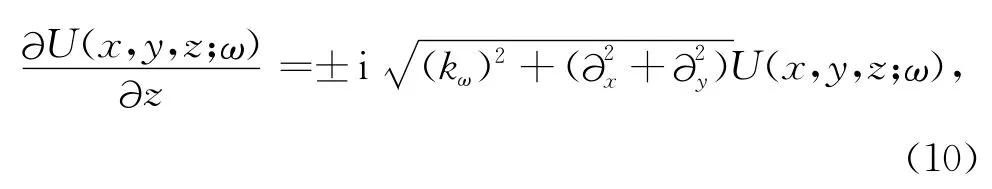
其中kω=ω／v，∂2x=∂2／∂x2，∂2y=∂2／∂y2.

黏声介质中单向波外推方程在频率空间域的表达形式如下：

其表达形式与声介质中单向波外推方程在频率空间域的表达形式一致，但是波数k由实数变为了复数.复波数kcω的表达形式有很多，不同的吸收衰减数学模型可以定义不同的复波数.此处，我们应用Kjartansson（1979）模型来表征吸收衰减模式，

各量的具体含义见（6）式的定义.公式（11）采用有限差分进行求解（Wang，2004；张立彬和王华忠，2010）.

由于波场外推公式是线性的，而平面波分解也是线性变换，所以可以利用波场外推算子直接外推合成的平面波道集，然后利用（9）式对外推后的结果成像，就完成了本文定义的黏声介质平面波叠前深度偏移.

关于吸收衰减补偿的控制，我们做了三个方面的处理，一是由于使用平面波偏移，仅对接收波场进行补偿处理，但是按双程传播效应进行补偿；二是可以仅对相位进行补偿，此时令（12）式中的衰减因子α=0；三是对振幅衰减和相位变化同时补偿，但控制因素考虑波场延拓深度（补偿效应是深度累积的）、高截止频率（高频补偿多，从（6c）式可以看出）、目标层的信噪比（把补偿后的信噪比控制在一定范围内）.

6 莺歌海地区的应用实例

为了充分说明黏声波偏移成像的必要性，我们设计如下的模型，及相应的数值试验.由于底劈现象引起的成像模糊由多种因素共同决定，本文侧重解决由于含气导致的地震波非弹性吸收衰减.因此试验设计的模型是与该区域实际地质模型相类似的模型，其速度模型和Q模型如图1所示.由于含气区域通常具有空间分布局域性，因此模型的Q模型仅在设计的含气区域存在较小的品质因子（吸收严重），而其他区域品质因子较大（不吸收）.正演所用的观测系统为：96炮；炮间隔：50m；道间隔：10m；震源函数为20Hz主频的Ricker子波.

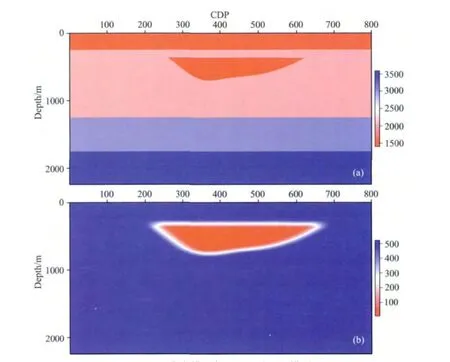
图1 （a）速度模型与（b）品质因子模型Fig.1 Velocity model（a）and Qmodel（b）

正演中分别模拟了声波数据（无吸收衰减）和黏声波数据（有吸收衰减）.图2为声波数据进行声波偏移的结果，该结果可作为理想的参照结果.图3为黏声波模拟数据采用声波偏移算法得到的结果，由图可以看出，含气区域下边界及以下区域存在严重的能量衰减，分辨率也有所下降.由此导致下覆地层振幅出现畸变，同相轴连续性变差.图4为本文方法结果（黏声波数据进行黏声波偏移），由图可以看出，由于含气区域导致的能量吸收和分辨率下降得到了很好地补偿，同相轴连续性和能量一致性得到了很好地恢复.图5为三个偏移结果在不同CDP点处的成像结果对比，由此可以看出，在含气区域外部，三者成像结果相当；而在含气区域，黏声波数据采用声波偏移的结果振幅具有严重的衰减，这将影响地震地质解释结果，而本文方法能够较好地补偿吸收衰减使得成像结果与无衰减情况下成像质量相当.因此，可以看出本文方法可以作为解决该地区存在的吸收衰减问题的合适的手段使用.

分析莺歌海某探区的声介质偏移成像结果可以看出成像模糊带分布在局部范围内，速度的横向变化也比较大.再考虑到海上数据单炮道集数量大，我们设计了黏声介质有限差分法平面波叠前深度偏移成像方法和程序，对该探区数据进行叠前深度偏移成像处理.

偏移成像所用参数如表1.

表1 实际数据测试所用的偏移成像参数列表Table 1 Migration parameter of the field data

图6是使用声介质三维平面波有限差分叠前深度偏移（图6a）与使用黏声介质三维平面波有限差分叠前深度偏移结果（图6b）的对比.由图可以看出，使用黏声介质三维平面波有限差分叠前深度偏移的成像剖面上的能量比使用声介质三维平面波有限差分叠前深度偏移的成像剖面上的能量得到了显著增强，同相轴能量的一致性也得到了提高.

图7是本次偏移所使用的Q模型示意图，由于浅层气吸收衰减严重且分布具有空间局域性，所以Q值仅在气云区较小（吸收严重），气云区外比较大（吸收较弱）.由图6可以看出只有波路径穿过该含气区域的能量得到了补偿.图8中对应的不同位置的成像道集也说明了气云区考虑吸收衰减补偿后成像效果的改进.

图2 声波数据进行声波偏移结果Fig.2 Acoustic migration result of acoustic data

图3 黏声波数据进行声波偏移的结果Fig.3 Acoustic migration result of visco-acoustic data

图4 黏声波数据采用黏声波偏移的结果Fig.4 Visco-acoustic migration result of visco-acoustic data

Q值的估计，目前主要有用于单道的叠后和叠前数据上的质心平移法（Quan and Harris，1997）和利用地震波振幅衰减的层析成像方法（Reine et al.，2012a，2012b；Cavalca et al.，2011）.也可以用测井信息来估计Q值.图7所示的Q模型是综合质心平移方法和该区岩石物理资料相结合建立的.从方法技术上讲，把质心平移方法和层析成像方法结合在一起是合适的方向.

图8为利用公式（9）得到的声介质和黏声介质中的地表炮域平面波成像道集对比.从图中可以看出使用黏声介质中的三维平面波有限差分叠前深度偏移成像道集能量得到了显著提升，模糊区的成像得到了一定程度的改善.

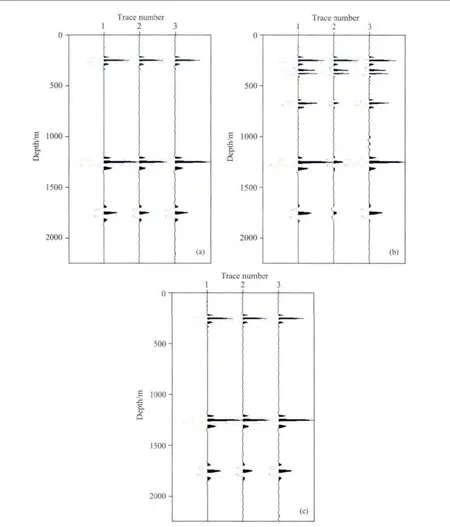
图5 不同CDP点处成像结果对比Fig.5 Migration results comparison at different CDP location

因此，对莺歌海地区成像模糊带而言，首先应该用叠前深度偏移成像方法产生道集，基于此建立比较精确的层速度场.在此基础上，考虑Q值引起的吸收衰减补偿.另一方面，由于拖缆长度普遍很长，尺度各向异性也要初步引入叠前深度偏移成像过程中，得到的模糊区的成像质量才会有质的提高.

7 结论与讨论

由于气体的上溢或浅层气的存在，成像存在模糊区的现象在莺歌海很多探区普遍存在.利用黏声介质叠前深度偏移进行吸收衰减补偿的成像是一种有效的改善模糊区成像的方法技术.

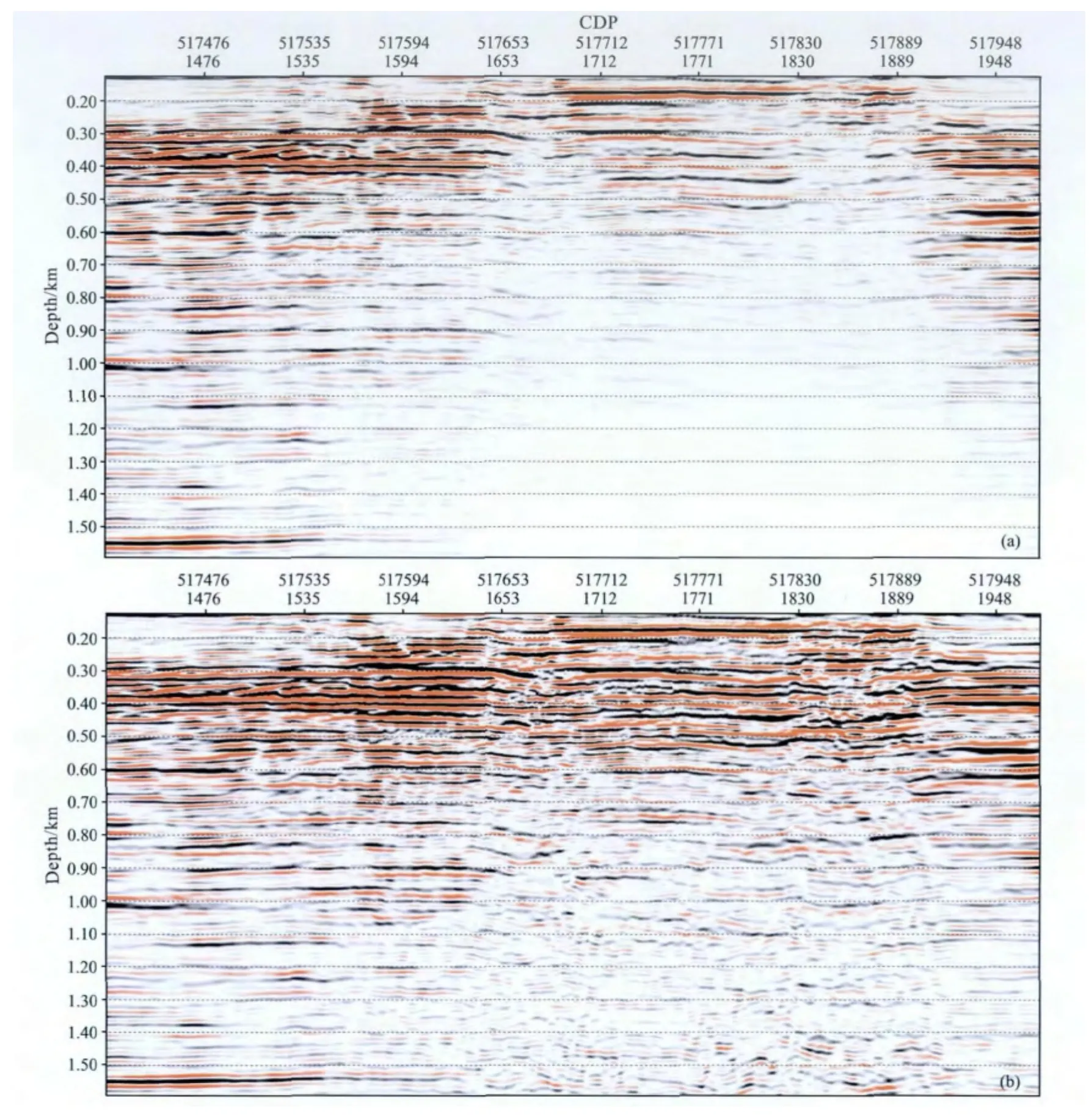
图6 （a）声介质与（b）黏声介质中叠前深度偏移结果对比Fig.6 Results comparison between（a）Acoustic and（b）Visco-acoustic migration

图7 Q模型分布图Fig.7 Qmodel

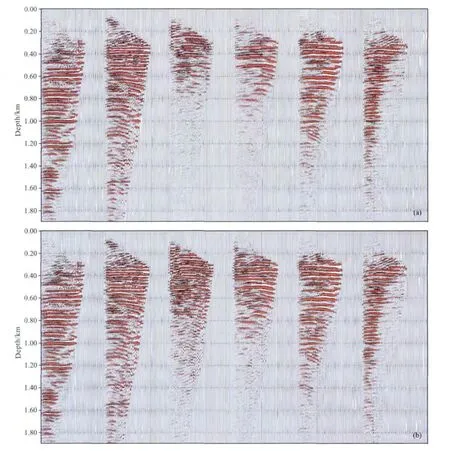
图8 （a）声介质与（b）黏声介质成像道集对比Fig.8 Imaging gathers comparison between（a）Acoustic and（b）Visco-acoustic migration

模糊区成像质量的改善，首先是偏移速度的更精确获取.在此基础上，吸收衰减补偿的效果才能发挥出来.品质因子Q的准确性远不及偏移速度的准确性那么重要，可以把它视为一个偏移参数.参数的好坏是可以按照成像的质量标准来定.当然，估计准确的Q值也是必要的.我们认为准确的Q值可以用来指示气藏的存在及丰度.

针对海上数据，要选择合适的偏移成像方法.首先要考虑偏移成像的效率.对于叠前深度偏移，陆上数据合适的单炮道集偏移在海上可能是不合适的，炮集数目巨大.炮集编码的叠前深度偏移成像方法可以大大提高深度偏移计算效率，对海上数据而言是合适的.但炮集编码叠前深度偏移方案设计不好会产生较为明显的成像噪音.平面波偏移也是一种炮集编码的叠前深度偏移方法.我们选择用平面波偏移就是基于这样的考虑.平面波采样比较合适时，成像噪音可以控制在很低的水平.

另一方面，由于南海地区成像模糊区是局部的，说明Q值的空间变化很强，必须选择有限差分法的偏移技术来适应Q的横向变换，而SSF（分裂步Fourier方法）、FFD（Fourier有限差分法）和广义屏等方法都不太适合用在莺歌海模糊区成像.

我们相信模糊区成像质量是可以较大幅度提高的，主要是考虑宽方位数据对模糊区反射层的充分照明；较精确的偏移速度、介质各向异性参数估计及Q值的估计，和吸收衰减；选择能同时适应横向变速、（至少）VTI介质和吸收衰减情形的、高效率的成像方法.

Bick el S H，Natarajan R R.1985.Plane-wave Qdeconvolution.Geophysics，50（9）：1426-1439.

Cavalca M，Moore I，Zhang L，et al.2011.Ray-based tomography for Qestimation and Qcompensation in complex media.／／SEG International Exposition and Annual Meeting.Expanded Abstracts，3989-3992.

Chopra S，Alexeev V，Sudhaker V.2003.High-frequency restoration of surface seismic data.The Leading Edge，730-738.

Feng B，Wang H Z，Liu S Y.2009.3Doffset plane-wave finitedifference pre-stack time migration.／／ SEG International Exposition and Annual Meeting.Expanded Abstracts，2934-2938.

Futterman W I.1962.Dispersive body waves.Journal of Geophysical Research，67（13）：5279-5291.

Hargreaves N D，Calvert A J.1991.Inverse Qfiltering by Fourier transform.Geophysics，56（4）：519-527.

Hu J T，Wang X W，Wang H Z.2011.Frequency grouping coding scheme for blended source imaging.／／ SEG International Exposition and Annual.Expanded Abstracts.

Kjartansson E.1979.Constant Q-wave propagation and attenuation.Journal of Geophysical Research，84（B9）：4737-4748.

Kjartansson E.1979.Constant Q-wave propagation and attenuation.Journal of Geophysical Research，84（B9）：4737-4748.

Mittet R，Sollie R，Hokstad K.1995.Prestack depth migration with compensation for absorption and dispersion.Geophysics，60（5）：1485-1494.

Mittet R.2007.A simple design procedure for depth extrapolation operators that compensate for absorption and dispersion.Geophysics，72（2）：S105-S112.

O’Doherty R F，Anstey N A.1971.Reflections on amplitudes.Geophysical Prospecting，19（3）：430-458.

Quan Y，Harris J M.1997.Seismic attenuation tomography using the frequency shift method.Geophysics，62（3）：895-905.

Reine C A，Clark R A，van der Baan M.2012a.Robust pre-stack Q determination using surface seismic data：Part I-Method and synthetic examples.Geophysics，77（1）：R45-R56.

Reine C A，Clark R A，van der Baan M.2012b.Robust pre-stack Q determination using surface seismic data：Part II-3Dcase study.Geophysics，77（1）：B1-B10.

Ren H R，Wang H Z，Zhang L B.2007.Compensation for absorption and attenuation using wave equation continuation along ray path.Geophysical Prospecting for Petroleum（in Chinese），46（6）：557-561.

Stoffa P，Sen M K，Seifoullaev R K，et al.2006.Plane-wave depth migration.Geophysics，71（6）：S261-S272.

Ursin B，Toverud T.2002.Comparison of seismic dispersion and attenuation models.Studia Geophysica et Geodaetica，46（2）：293-320.

Van der Baan M.2012.Bandwidth enhancement：Inverse Q deconvolution or time-varying Wiener filtering.Geophysics，77（4）：V133-V142.

Wang H Z，Ma Z T，Cao J Z.1998.3Done step migration using optimized coefficient paraxial equation.Oil Geophysical Prospecting （in Chinese），33（2）：170-184.

Wang H Z.2002.A stable and efficient approach of inverse Q filtering.Geophysics，67（2）：657-663.

Wang H Z，Zhang L B，Ma Z T.2004.Seismic wave imaging in visco-acoustic medium.Science in China Ser.A Mathematics，47（1）：146-154.

Wang H Z.2008.Inverse-Qfiltered migration.Geophysics，73（1）：S1-S6.

Zhang J，Wapenaar K.2002.Wave field extrapolation and prestack depth migration in anelastic inhomogeneous media.Geophysical Prospecting，50（6）：629-643.

Zhang L B，Wang H Z.2010.A stable inverse Qmigration method.Geophysical Prospecting for Petroleum （in Chinese），49（2）：115-120.

附中文参考文献

任浩然，王华忠，张立彬.2007.沿射线路径的波动方程延拓吸收与衰减补偿方法.石油物探，46（6）：557-561.

王华中，马在田，曹景忠.1998.优化系数傍轴近似方程三维一步法偏移.石油地球物理勘探，33（2）：170-184.

张立彬，王华忠.2010.稳定的反Q偏移方法研究.石油物探，49（2）：115-120.