带LCL滤波器的单相并网逆变器低频振荡现象分析

周 林，龙崦平，张 密，晁 阳，郑光辉

（重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400030）

0 引言

随着光伏发电、风力发电等新能源发电技术迅速发展，并网逆变器得到了广泛的应用[1-3]，因此并网逆变器成为学者近年来研究的热点。由于逆变器属于强非线性电路，在一定条件下会表现出某些复杂的不规则行为，这可能导致系统的不稳定，影响系统的正常并网运行。这是工程设计和维护运行中需要注意的问题。

针对H桥变换器中出现的非线性行为，国内外已经有了一定的研究[4-12]。 早在 2002年，Robert等以电流模式下H桥直流斩波器为研究对象，分析了其中的边界碰撞分岔现象，并建立了H桥变换器的离散模型[4-6]，为后续的研究工作奠定了基础。在国内，王学梅等首次研究了比例调节下H桥逆变器中的分岔与混沌现象[7-9]，将混沌研究由斩波器推广到逆变器中。文献[10]对模拟PI调节下的电压控制型逆变器中出现的快标分岔行为进行了研究，并利用系统Jacobian矩阵对系统进行了稳定性分析。文献[11]则对数字控制下的单相逆变器中出现的振荡现象进行了深入的研究，揭示了系统发生振荡现象的内在机理。然而，上述有关H桥变换器的研究都只是集中于独立运行或离网运行的系统中。随着新能源发电等的广泛推广，并网运行系统成为了主要的发展方向。因此，研究并网逆变器中出现的复杂行为具有重要的理论意义和工程实践价值。

LCL滤波器具有对高频分量呈高阻抗的特性，对高频谐波电流具有很大的衰减作用，因此常应用于大功率场合。随着大型分布式发电的逐渐推广，LCL滤波器具有很好的应用前景。因此，本文以带LCL滤波器的单相并网逆变器为研究对象，建立了系统的离散迭代模型，并利用Jacobian矩阵对系统进行了稳定性分析，揭示了系统出现低频振荡现象是由于其发生了Hopf分岔，并对系统的分岔点做出了准确预测。同时，根据系统的特征方程确定了系统发生失稳后的振荡频率。MATLAB/Simulink仿真和实验都验证了理论分析的正确性。

1 电路工作原理及仿真现象分析

1.1 并网逆变器工作原理

本文以典型的带LCL滤波器的单相全桥并网逆变器为研究对象，其电路工作原理如图1所示。图中，E为逆变器直流侧电压，VT1—VT4为IGBT开关管；逆变器输出端经LCL滤波器后并入电网ug=Umsin（2πfst），其中 Um和 fs分别为电网电压幅值和频率；滤波器电感电容值分别为L1、L2和C，R1和R2分别表示电感L1和L2的寄生电阻值。

图1 单相并网逆变器电路原理图Fig.1 Schematic diagram of single-phase grid-connected inverter

系统控制部分采用的是并网电流和电容电流双闭环控制策略[2]，其中电容电流内环为系统增加阻尼，有效抑制系统谐振；入网电流外环控制用来实现高功率因数并网。具体控制过程如图1所示，iref=Imsin（2πfst）为外环参考电流，入网电流 i2与参考电流的误差信号经外环比例控制器kp后，为电容电流iC内环控制提供参考信号，kc为内环比例控制系数。另外，为克服电网电压对入网电流的干扰，需要加入电网电压前馈通道，图中kpre为电压前馈控制系数。最终得到调制信号ucon经峰值为1的三角载波调制后形成SPWM波来驱动各个开关管工作，系统开关频率为f。

根据电力电子开关工作状态，以逆变侧电流i1、入网电流i2以及电容电压uC为状态变量，系统工作状态可以描述为：

当 σ=1 时，开关 VT1、VT4导通，VT2、VT3关断；当σ=0 时，开关 VT2、VT3导通，VT1、VT4关断。 根据平均的思想，将占空比D代替式（1）中的σ即可得到系统的平均模型[12-13]，并由 SPWM 原理可知[14]，占空比由下式决定：

其中，Utri为三角载波的峰值；ucon为调制信号，由控制部分原理图可知：

1.2 MATLAB/Simulink仿真现象分析

根据上述系统的工作原理，利用平均模型建立了系统的Simulink数学仿真模型，系统参数选取如下：E=350 V，L1=2.0 mH，R1=0.15 Ω，C=15 μF，L2=0.8 mH，R2=0.1 Ω，Um=311 V， fs=50 Hz，Im=5 A， f=20 kHz，kc=0.25，kpre=1/350。 可以得到 kp分别取 1.0 和1.65时系统入网电流i2波形、i2-uC的相轨迹图以及对应的FFT分析结果，如图2、3所示。

从图2各子图中可以看出，当kp=1.0时，系统入网电流谐波畸变率（THD）为0.35%，且波形光滑稳定，可见系统此时处于稳定状态。随着kp取值的增大，从图3各子图中可以看出，当kp=1.65时系统入网电流波形产生了低频振荡现象，系统已经处于不稳定状态，对应的FFT分析结果表明其振荡频率约为1870 Hz。

上述仿真结果表明随着控制器参数的变化，系统的状态变量波形由稳定变成发生低频振荡，表明系统由稳定进入了不稳定状态。这种振荡会严重影响系统性能，导致入网电流畸变，影响电网运行。因此，对这种振荡现象做进一步分析有其重要意义。

图2 kp=1.0时的仿真结果Fig.2 Simulative results when kpis 1.0

图3 kp=1.65时的仿真结果Fig.3 Simulative results when kpis 1.65

2 系统的稳定性分析

为对系统进行稳定性分析，本文采用频闪映射法首先对并网逆变器系统进行离散建模。由于系统外环参考电流以及电网电压都为正弦信号，因此系统为一时变系统。但因为系统参考信号的频率fs远小于系统的开关频率f，利用准静态分析的思想可认为在一个开关周期内参考信号及电网电压为一恒定值[11]。因此，第n个开关周期内的电网电压值和参考电流值可以表示为：

2.1 系统的离散建模

首先对系统的主电路进行分析，可知在一个开关周期T内系统将出现2个工作状态，系统的状态方程可以表示为：

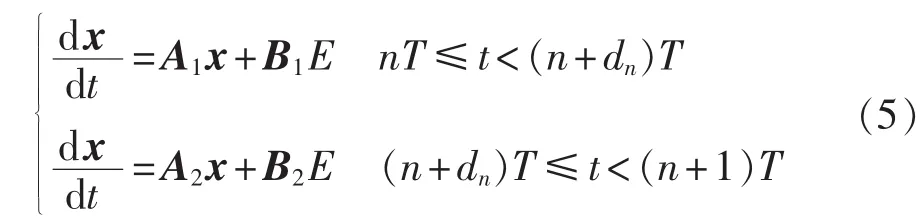
利用频闪映射的思想建立上述状态方程的离散迭代模型如下：

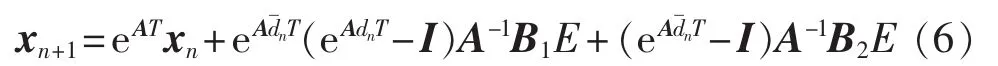
对控制部分可根据图1中的系统控制规律，并结合式（2）、（3）即可知第n个开关周期的占空比dn由下式决定：

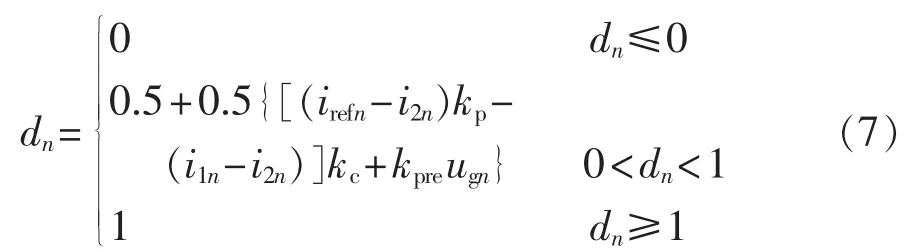
则式（6）、（7）构成了整个系统的离散模型。

2.2 稳定性分析

本文采用Jacobian矩阵对系统进行稳定性分析，因此首先需对系统的平衡点进行求解。根据系统的平均模型可知，系统的平衡点可通过令式（1）中的导数为零来得到[13]，于是某个开关周期内系统的平衡点 XQ=（I1Q，I2Q，UCQ）可以表示为：

其中，Iref和Ug表示此开关周期内的参考电流及电网电压采样值，因此可认为是一个恒值。平衡点处系统的占空比可表示为：

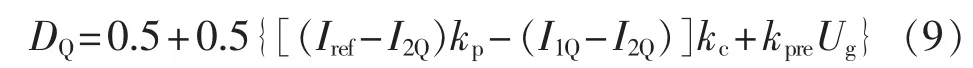
于是根据离散迭代模型可以得知，系统的Jacobian矩阵为：

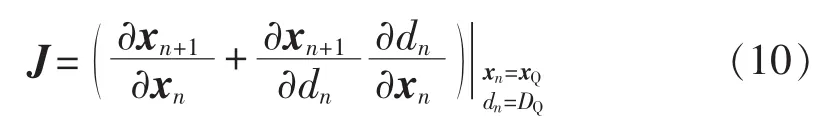
结合式（8）、（9）、（12）即可求得系统 Jacobian 矩阵的特征值。然后，根据Jacobian矩阵稳定性判据，当系统参数kp变化时，可以通过判断系统Jacobian矩阵的最大模特征值是否越出单位圆来确定系统是否稳定。

系统参数同1.2节，利用MATLAB对系统进行数值仿真。可以得出随着系统外环调节系数kp在0.1～1.8之间变化，系统Jacobian矩阵的特征值的变化情况，如图4所示。可以看出，随着kp的增大，系统的3个特征值中，λ1在实轴上变化，另一对特征值λ2和λ3互为共轭复数。表1为Jacobian矩阵特征值随kp的变化情况。可以看出，在kp=1.5时，这一对共轭复数特征根同时穿越了单位圆，可见此时系统发生了Hopf分岔现象，kp=1.5即为系统的Hopf分岔点。

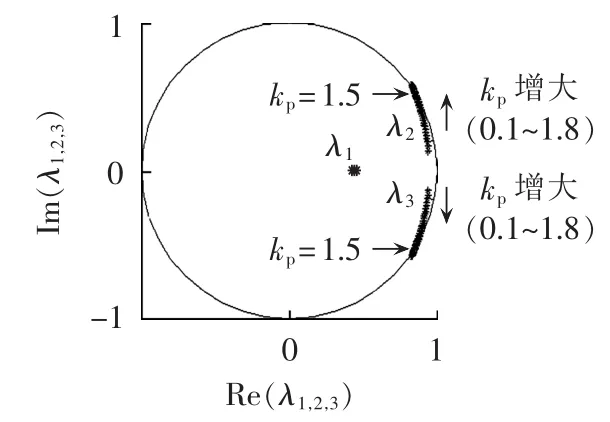
图4 系统特征值随着kp的变化轨迹Fig.4 Variation of system eigenvalues along with kp

表1 Jacobian矩阵特征值随kp的变化情况Tab.1 Variation of Jacobian matrix eigenvalues along with kp

另外，为了更清晰地分析系统中其他控制参数的变化对系统稳定性的影响，本文通过寻找系统Jacobian矩阵最大模特征值的过“1”点，得出了控制参数kp和kc同时变化时系统运行稳定域的分布图，如图5所示。可以看出随着kp和kc的同时增大，系统的稳定运行域逐渐减小。因此，利用系统的稳定域分布图可以对系统进行优化设计。

图5 系统稳定域分布图Fig.5 Distribution of system stability regions

2.3 系统Hopf分岔振荡频率的确定

为确定系统的振荡频率，本文通过分析系统特征方程的根来确定系统的振荡频率。若变换器有一个极点出现在复平面的右半平面上，则系统是不稳定的，其输出就会存在低频振荡现象[14-16]。对于一个存在振荡的三阶系统，其3个极点可以表示为p1=P，p2=α+jω，p3=α-jω，其中 ω 即为系统的振荡频率。

通过本文系统的平均模型，结合式（1）—（3）可以得到系统参考电流iref到入网电流i2的传递函数，则可知系统的特征方程为：

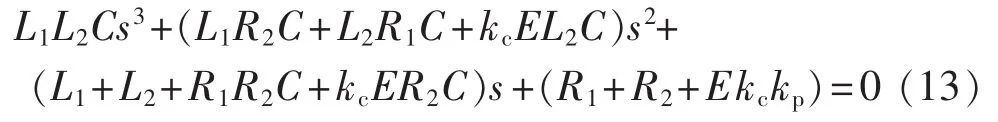
为求解上述一元三次方程，首先令a=L1L2C，b=L1R2C+L2R1C+kcEL2C，c=L1+L2+R1R2C+kcER2C，d=R1+R2+Ekckp，则上式可变为：

利用式（13）—（17），结合系统参数可以求得，当kp=1.6时，系统的振荡频率为fos=1865.7 Hz。可见，系统振荡频率的理论计算值与第2节中的FFT分析结果相吻合，验证了通过该方法确定系统振荡频率的可行性和有效性。

3 实验验证与结果分析

为验证本文有关并网逆变器低频振荡现象分析结论的正确性，采用RT-LAB实验平台对系统中产生的动力学行为进行了实验分析。实验主电路由实物搭建而成，控制部分由RT-LAB平台实现。为实验方便，本文实验过程中降低了系统电压等级，选择实验参数如下：E=50 V，Um=15 V，Im=2 A，f=8 kHz，kpre=1/50，L1=5.3 mH，L2=1.8 mH，C=3.3 μF，其他参数同1.2节。通过上述理论分析方法，可以得出结论，当kp=1.45时系统出现Hopf分岔点。

实验结果如图6所示，图6（a）显示的是当kp=1.1时入网电流和并网电压的实验波形图，可以看出此时电流波形为光滑的正弦波，系统处于稳定状态；当kp=1.5时，入网电流以及并网电压波形如图6（b）所示，可见此时系统已经发生Hopf分岔并出现了低频振荡现象；图6（c）则示出了当kp=1.5时，利用示波器对入网电流进行FFT分析的结果，发现此时系统发生振荡的频率约为880 Hz，而理论分析得到的在实验参数下系统的振荡频率为874.2 Hz。可见理论分析与实验结果相吻合。

图6 ug与i2实验波形Fig.6 Experimental waveforms of ugand i2

因此可以得出结论，随着kp值的增大，并网逆变器会出现低频振荡现象，这将会严重影响系统的并网运行。

4 结论

以带LCL滤波器的单相并网逆变器为研究对象，本文将非线性系统的动力学行为研究由离网变换器推广到了并网逆变器中。推导了带LCL滤波器的单相并网逆变器的离散迭代模型。利用系统的Jacobian矩阵，对系统进行了稳定性分析，结果表明，随着调节系数的变化，系统将由稳定状态发生Hopf分岔，致使系统出现低频振荡现象。根据Jacobian矩阵最大模特征值的变化情况，对系统运行的分岔点做出了准确的预测。同时，利用系统的特征方程，给出了出现振荡现象时系统振荡频率的确定方法。通过MATLAB/Simulink仿真与 RT-LAB实验验证了理论分析的正确性。本文研究将非线性系统的动力学研究推广到了一个新的应用对象，为工程设计中防止低频振荡现象的发生提供了重要指导。