分布式电源接入配电网多目标优化规划

栗 然，马慧卓，祝晋尧，王义贺，胡 博

（1.华北电力大学 新能源电力系统国家重点实验室，河北 保定 071003；2.国网河北省电力公司电力科学研究院，河北 石家庄 050021；3.华北电力大学 控制与计算机工程学院，北京 102206）

0 引言

分布式电源（DG）指分布在负荷点附近的小容量电源，作为微网的重要组成部分，具有投资少、发电方式灵活、环保等优点。DG接入配电网后，从技术角度考虑会给电力系统运行带来问题，但同时也带来了诸多效益，如减小网损、提高系统安全性、延缓设备升级投资等[1]。

DG的规划问题，一般包括选址和定容2个方面。文献[2]从系统网损最小出发考虑DG接入选址问题，未曾考虑投资成本等因素。文献[3-5]以总费用为目标函数建立了优化模型，却没有考虑DG接入对系统运行带来的影响。文献[6]以DG最大接入容量为目标函数进行选址优化。文献[7-8]考虑了多阶段的DG选址定容问题。文献[9-12]建立了DG规划多目标模型，但优化过程中将多目标模型转化为单目标处理，不能独立地研究分析各目标作用。文献[13-14]虽然考虑了多目标技术，但皆从2个角度考虑优化问题，考虑不够全面。

现行的多目标优化理论对多目标进行处理时，常见方法是转化为单目标进行优化，这样的处理方法不能得出各个目标间的内在联系，即使采用各目标独立寻优，在面临最终决策的过程中仍会面临考虑因素单一的局面。

针对以上论述，本文立足于电力系统角度，以投资及运行成本、网损、电压指标3个方面独立衡量DG接入配电网后对系统的影响，并基于此建立优化模型。提出基于熵和距离的多目标粒子群优化（DEMPSO）算法作为寻优技术；提出模糊多权重（FMW）技术作为方案决策手段，弥补了现行优化算法的缺陷，进行DG接入配电网的优化选址与定容。

1 数学模型

电力系统的基本要求是保证可靠的持续供电、良好的电能质量和运行的经济性。依据以上要求，针对配电网中DG选址问题，从投资及运行成本、网损、电压及电压稳定性3个角度进行优化选址和定容计算。选取投资及运行成本作为优化目标体现了运行的经济性；网损是电力系统运行的一项重要经济指标，故将其作为优化目标；将电压和电压稳定性作为优化目标则是从电能质量角度出发。综合以上3个方面可以更加完善地解决DG优化选址定容问题。此外，DG具有发电方式灵活、环境友好性等优点，将DG接入配电网有着广阔的前景。

文献[4]中，对DG规划问题建立了数学模型，但该模型中基于单目标考虑，不能得出各个目标间的内在关系。本文在文献[4]基础上，将该文献目标函数中的网损作为单独目标函数，并引入电压稳定指标，共同构成了DG优化规划多目标数学模型。

1.1 投资及运行成本

目标函数由3个部分构成。

a.线路升级费用。考虑到因配电网负荷增加，会导致一些线路超过额定运行容量，增加投资成本。

b.变电站扩展及运行费用。当变电站超过额定运行容量时，考虑增加变电站变压器台数，会增加投资成本。

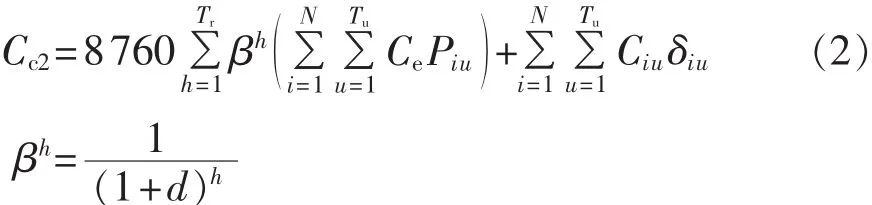
c.DG的投资及运行费用。包括DG的初始投资和基准年至规划年的运行费用。

考虑以上因素，费用目标函数[4]最终为：

其中，N为系统的节点数；M为负荷点数；NDG为DG的安装点数；Tu为变电站变压器台数；Cij为线路i-j的固定升级费用；Ce为购电电价；Ciu为变压器投资费用；Cri为第i台 DG固定投资费用；Cfi为第i台DG年运行费用；Tr为规划水平年；β为当前价值因子；d为贴现率；Piu为第u台变压器于节点i分配的功率；pf为系统的功率因数；SDGi为第i个DG可行安装点的DG出力；δij为线路i-j的升级决策变量；δiu为变压器二元决策变量；δDGi为第i台DG的二元决策变量。

1.2 网损

网损是衡量配电网运行的重要经济指标，DG的合理接入会减小系统网损，故选取网损作为目标函数。

其中，Ui、Uj为节点电压；Yij为线路导纳；θij为线路i-j的阻抗角；δji为节点电压相角差。

1.3 电压指标

电压指标包括节点电压偏差和支路电压稳定性指数。电压偏差指标指各节点与系统正常电压值偏差之和，电压稳定性指标指各个支路电压稳定性指数之和。这2个因素的综合考虑可以衡量电能质量的高低。

其中，u2为配电网潮流计算中基于解的存在性的电压稳定指数[15]，反映了支路的电压稳定裕度；Uiref为系统各节点正常运行时的电压幅值；Pij、Qij、Rij、Xij分别为线路ij的有功功率、无功功率、电阻和电抗。

综合两方面，赋权重构成电压指标：

其中，ω1、ω2为权重。

综上所述，考虑以上3个角度作为优化目标，形成目标函数，运用DEMPSO算法和FMW进行优化计算。

1.4 约束条件

a.等式约束条件。

等式约束条件为系统的潮流约束：

其中，Sij、Sji为线路功率；Dej为 j点负荷需求；Zij为线路阻抗。

b.不等式约束条件。

不等式约束条件包括节点电压约束、DG运行容量约束、线路容量约束和变电站容量约束，分别如式（10）—（13）所示。

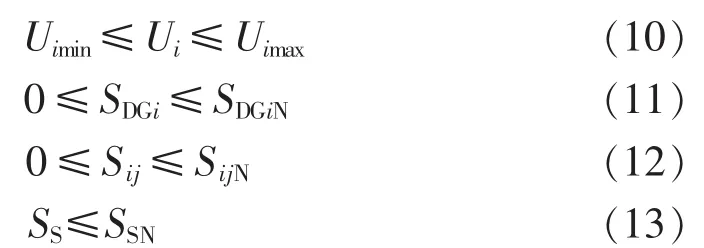
其中，Uimax、Uimin为节点电压上、下限；SDGiN、SijN、SSN分别为DG安装容量、线路额定传输容量、变电站额定容量。

2 优化算法

多目标优化与单目标优化的本质区别在于：多目标优化问题的解不唯一，而是存在一个解集，称之为Pareto最优解或非支配集。Pareto最优是指不能再改善某些境况，而不使任何其他境况受损。

设有m个优化目标，彼此之间可以互相冲突，优化目标函数可以表示为：

Pareto最优解由Vilfredo Pareto提出，定义为：称是最优解，若满足：

或者至少存在一个j，使：

其中，I为可行解个数，F为满足约束条件的可行解解集，即：

由定义可知，一般情况下最优解并不止一个，而是形成一个集合，而多目标算法的寻优过程就是构造非支配集，并使非支配集逐步逼近Pareto前端。

粒子群优化（PSO）算法是Eberhart和 Kennedy在对一个简化社会模型进行仿真时受到启发而提出的，其思想源于群体组织社会行为，通过个体间的协作寻找最优解[16]。 Carlos A Coello Coello 将 Pareto技术与PSO算法相结合，形成了多目标粒子群优化（MOPSO）算法[17]。

与遗传算法相比，PSO算法收敛速度快，优化效率高，目前已在电力系统诸多复杂优化领域得到了应用。

2.1 PSO算法

PSO算法结构简单，能够有效地优化各种函数。在PSO算法中，每个寻优个体称为一个粒子，每个粒子代表一个潜在的解。在一个D维目标搜索空间中，每个粒子是空间内的一个点，设粒子群由m个粒子构成，m也被称为粒子群的规模，过大的m值会影响PSO算法的运算速度和收敛性。

PSO算法数学描述为：在一个D维空间中，由m个粒子组成的粒子群 X=（x1，…，xi，…，xD），其中第 i个粒子位置为 xi= （xi1，xi2，…，xiD）T，速度为 vi= （vi1，vi2，…，vid，…，viD）T，其中，每个粒子个体极值为 pi=（pi1，pi2，…，piD）T，寻优种群的全局极值为 pg=（pg1，pg2，…，pgD）T，按照追随当前最优粒子的原理，第 i个粒子将按式（15）和式（16）更新速度和位置。

其中，j=1，2，…，D；i=1，2，…，m，m 为种群规模；t为当前进化代数；ω 为惯性权重；r1、r2为分布于[0，1]之间的随机数；c1、c2为加速常数。 由式（15）可知，每个粒子的速度更新表达式由三部分组成：第1部分为粒子先前的速度；第2部分为“认知”部分，表示粒子自身的思考；第3部分为“社会”部分，表示粒子间的信息共享与相互合作。

本文对MOPSO算法进行了改进，在其基础上引入熵与评判因子，形成了DEMPSO算法，能够快速合理地找到Pareto前端。

2.2 权重调整

定义进化因子：

其中，fimean（i=1，2，…，m）为粒子第 i个目标函数适应值的平均值。由定义知进化因子反映了粒子进化的快慢，当e趋近或保持在1时，算法停滞或是找到了最优值。进化因子的提出衡量了非支配集更新的快慢。

定义粒子的聚集度因子：

其中，fip为粒子第i个目标函数最优粒子的适应值。聚集度因子反映了粒子的聚集程度，同时也反映了粒子的多样性，当g趋近于1时，粒子具有同一性，若此时陷入局部最优则不容易跳出局部极值点。

引入平均聚焦距离[18-19]和最大聚焦距离：

其中，m为粒子个数，D为每个粒子的维数，xibest（d）为目前搜到的最优粒子各维最优值，本算法中为非支配集中所有粒子各维的平均值；xid为第i个粒子d维的值。

由以上各式给出聚焦距离变化率概念。

聚焦距离变化率从粒子间的空间距离角度反映了粒子的聚集程度与多样性。聚焦距离变化率较大，表明粒子全局搜索能力较差，应使粒子尽快地进入全局搜索，相反即应提高粒子局部搜索能力。

e、g、kr分别从粒子的进化速度、适应值、粒子间的空间距离3个方面反映当前寻优的状况，考虑因素更加全面。综合以上3个因子共同动态调整权重，定义评判因子：

引入自适应非线性惯性权值递减函数动态调整权重，经测试惯性权重更新表达式如下。

2.3 熵的引入

定义成功阈值系数sc、fc用于动态调整粒子更新表达式。

当粒子当前的适应值优于前一次迭代适应值时定义为迭代成功，反之为迭代失败。随着优化的进行，sc、fc不断地动态调整，调整规则如下：

当连续成功次数达到sc时，粒子位置调整为：

连续失败次数达到fc时，速度更新公式变为：

其中，xiworst为全局最差位置粒子的各维值，c为加速常数，r为分布于[0，1]之间的随机数。

熵反映了系统的混乱程度，粒子在快速收敛时sc继续加速收敛，相当于引入负熵；粒子趋于稳定时fc使得粒子的混乱度增加，相当于引入正熵，有利于跳出局部极值，通过这2个系数的共同作用，改变粒子的多样性。

通过MATLAB编程，本文应用以下3个常用数学函数对算法进行了测试：

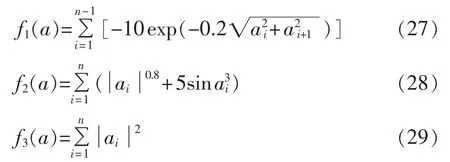
测试结果如图1所示。

图1 Pareto解集分布对比图Fig.1 Comparison of Pareto set distribution

由图1中对比分析可知，DEMPSO算法较之原始MOPSO算法更加完整地找到了Pareto前端，形成的前端更加光滑完整。

在DG优化选址的背景下，DEMPSO算法的主要优化流程如图2所示，约束条件处理如图3所示。

图2 DEMPSO算法流程图Fig.2 Flowchart of DEMPSO algorithm

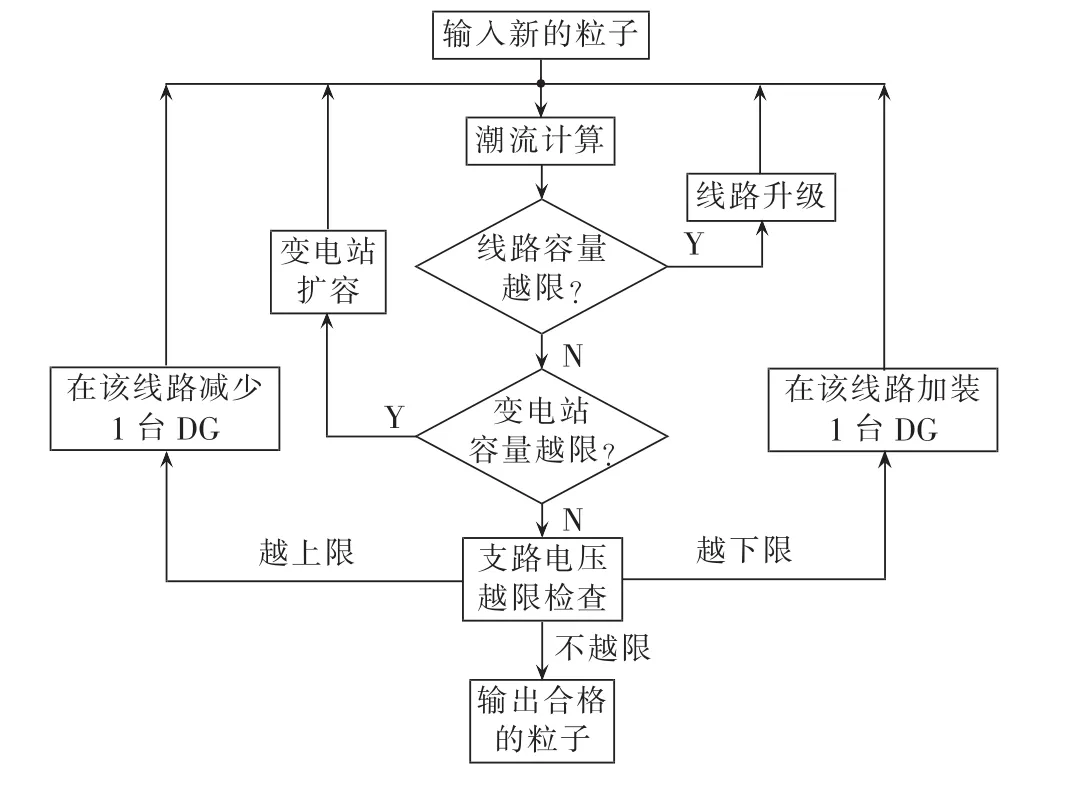
图3 约束条件的处理Fig.3 Processing of constraints

本文提出的DEMPSO算法可以有效地防止算法陷入局部最优，能形成分布良好的Pareto前端。

3 决策技术

依据C.L.Huang和A.S.Masud提出的由决策者偏爱信息表达方式的划分原则，分为事先评价法、事中评价法、事后评价法，利用DEMPSO算法进行多目标优化属于事后评价法。

由于得到Pareto非支配集之后，得到一组可行解解集，从解集中选择出理想方案属于事后评价过程。本文定义了一种新型的FMW技术，依据实际情况，赋予每个非劣解多个权重，进行事后决策，这种处理方法弥补了传统方法中进行决策时目标函数处理方式单一的缺陷。以本文DG选址优化为范例，思路如下文所示。

3个目标函数作为参与决策的3个方面，首先对非支配集中方案进行模糊分级评价，根据分级和相应的权重确定各个非劣解的收益指数，最终收益指数最大者为最优方案。

利用模糊技术确定各个可行解隶属于目标函数分级的隶属度，隶属函数如图4所示。

图4 隶属函数Fig.4 Membership function

对每一个目标函数都进行分等级隶属度的划分，通过这个步骤，每一个非劣解都可形成MS×NS（MS为目标函数个数，NS为各目标函数划分等级数）个隶属度，用于评价此非劣解的优劣。

Pareto非支配集中每个方案的评价指标变为：

其中，Cl、Cm、Ch，Ll、Lm、Lh和 Ul、Um、Uh分别为低、中、高3级目标函数的费用、网损、电压指标；q为目标函数个数。

δObji值最大的非劣解即为最优解。传统的决策方法中，都是通过对目标函数简单赋权重来确定最优方案，而优化算法得到的Pareto非支配集中并不是全部趋向于各个目标函数都为最优的趋势，而是在各个目标函数分级当中都包含一定的隶属度，决策者的偏好信息会对决策过程产生影响。FMW通过对目标函数进行分级多权重处理，弥补了传统决策方法的不足，可以从更宽广的范围寻找到更符合决策者要求的决策结果。

4 算例分析

算例的网架结构如图5所示[4]，该系统包括一个 132kV /33kV 的变电站（容量 40MV·A）、8条馈线和8个负荷点。每条线路额定容量为15MV·A，单位阻抗Z12MVA=0.1738+j0.2819 Ω/km。预计4年后负荷增长28%，达到51.1 MV·A，系统的功率因数为0.9，DG的单位容量为0.1 MV·A，每条线路允许接纳的DG容量上限为4 MV·A，考虑变电站扩容时，将会购进2台三相10 MV·A变压器（132 kV/33 kV），线路传输容量越限时，每条馈线升级为额定容量为20MV·A的线路，升级后线路的单位阻抗变为Z20MVA=0.1469+j0.2719 Ω/km，系统允许的最大电压偏差为5%。市场电价为70$/（MW·h）。DG类型考虑使用燃气轮机，燃气轮机的造价为 0.5×106$/（MV·A），运行费用为 50$/（MW·h）。 每台 10 MV·A 变压器费用为$200 000，线路升级费用为0.15×106$/km，贴现率为12.5%。

图5 算例网架结构Fig.5 System structure for case study

负荷情况和线路参数如表1、2所示。

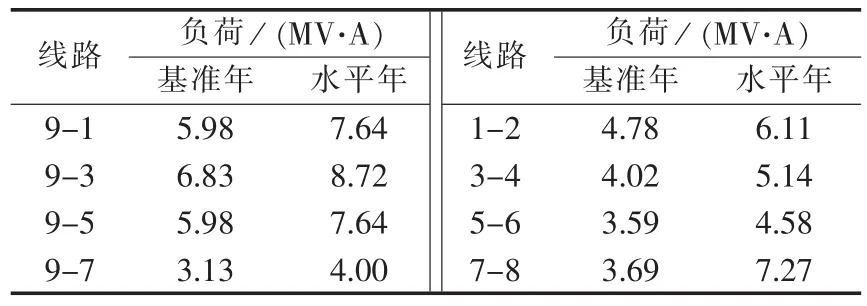
表1 负荷情况Tab.1 Load condition

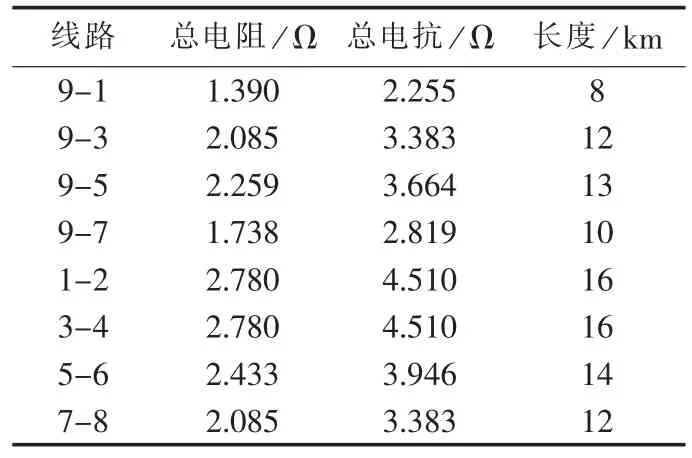
表2 线路参数Tab.2 Parameters of transmission line

4.1 可行方案池形成

针对优化算例，运用DEMPSO算法进行计算，生成Pareto前端，构成非支配集，具体案例中本文将非支配集称为可行方案池SP（Scheme Pool），SP中囊括了所有的可行方案，每一种方案都包括了DG的位置和容量选择信息，且各方案间的优劣不可互相比较。进行初始化，粒子个数设置为100，迭代次数400，优化结果如图6—10所示。

由图6对比分析可知，DEMPSO算法较之原始MOPSO算法搜寻到了更多的非劣解，更加完善了DG优化选址的可行方案，形成的前端更加光滑完整。

图6 Pareto解集分布对比图Fig.6 Comparison of Pareto set distribution

图7展示了DEMPSO算法三目标函数寻优的Pareto前端空间分布及投影图，Pareto前端由4394个非劣解组成。在空间中，Pareto最优解形成了2条Pareto前端，这是由于约束条件中线路传输容量越限时升级所致。每条馈线的额定容量为12 MV·A，传输容量越限时线路升级为额定容量20 MV·A，由于线路升级费用及升级后对系统的影响，形成了含线路升级和非升级方案的2条Pareto前端。

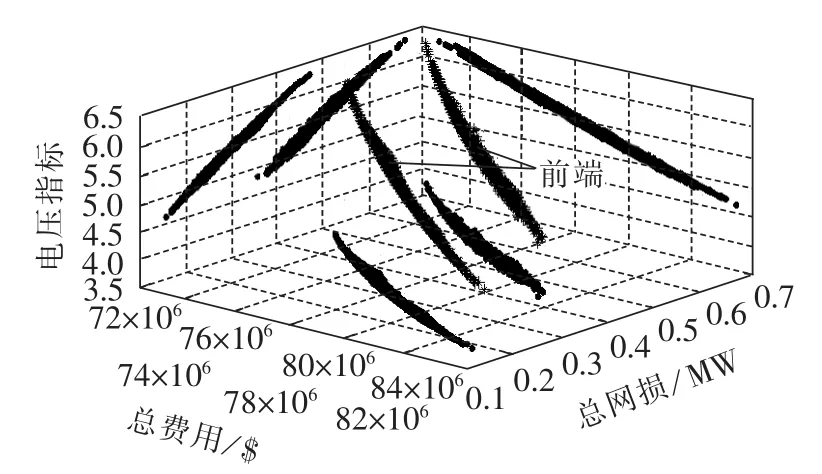
图7 Pareto解集分布图Fig.7 Pareto set distribution

由图8知，总投资费用相同时，线路升级方案有利于降低网损。由图9知，总投资费用相同时线路升级方案具有更高的电压指标。由图10知，总网损相同时的线路升级方案策略具有更低的电压指标。线路是否升级，会影响2条Pareto前端的分布。

图8 总费用、网损投影图Fig.8 Total cost and projective net loss

图9 总费用、电压指标投影图Fig.9 Total cost and projective voltage index

图10 网损、电压指标投影图Fig.10 Net loss and projective voltage index

4.2 最终方案决策

生成SP后，依据投资方的偏好信息，运用FMW进行决策，得出不同偏好信息下的最优DG选址与定容方案。为便于与传统决策手段对比，本文采取了5种方案进行比较。

方案1：利用文献[3]采用的模糊技术进行决策。方案2：利用本文提出的FMW技术进行决策，侧重于总费用。方案3：利用本文提出的FMW技术进行决策，侧重于总网损。方案4：利用本文提出的FMW技术进行决策，侧重于电压指标。方案5：利用本文提出的FMW技术进行决策，3个目标函数的重视程度相同。

表3对比了5种方案的总投资费用，方案1、4为非线路升级方案。其中方案1为传统模糊决策得到的最优方案，该方案中考虑因素单一，不能体现出各目标函数对最终决策的影响；方案4为FMW技术偏重电压稳定指标得到的最优方案，要求系统中装入的DG容量达到了35.4MV·A，DG的大量接入可以减小变电站的运行费用，但增加的DG投资费用使得总费用大于其他4种方案；方案2中，采取了线路升级，偏重于总投资费用，线路升级后系统接入的DG容量为26.6MV·A，为5种方案中最小DG接入容量；方案3偏重于网损的减小，该方案中要求线路升级，线路升级后接入较多的DG以达到更优地减小网损，DG接入容量为29.9MV·A；方案5为综合方案，各个目标函数分级权重相同，该方案与方案1相比，总投资费用更小，DG接入容量为29.6MV·A。

表3 最终方案费用对比Tab.3 Comparison of costs among final schemes

图11展示了5种方案中，各节点DG接入容量（直方图）与节点电压（曲线图）之间的关系。每种方案均在线路的末端节点装设了4 MV·A的DG，达到了线路要求的DG接入容量上限。几种方案中方案2、3、5为线路升级方案，线路1-2升级后，极大改善了电压跌落的状况，使得节点2的电压由32.2 kV提升至32.9 kV左右。图中所示5种方案，电压幅值皆可以较好地满足系统正常运行的要求。

图12反映了5种方案的电压稳定性指标，该指标数值越小则线路的电压稳定裕度越大，接近1时到达静态电压稳定极限。方案4的电压指标最好，是因为该方案中接入了大量的DG，使得线路上传输的功率大幅减少，导致电压稳定裕度变大，此方案的缺点是增加了投资；其余4种方案皆具有良好的静态电压稳定性。

图11 5种方案电压对比图Fig.1 Comparison of voltage among five schemes

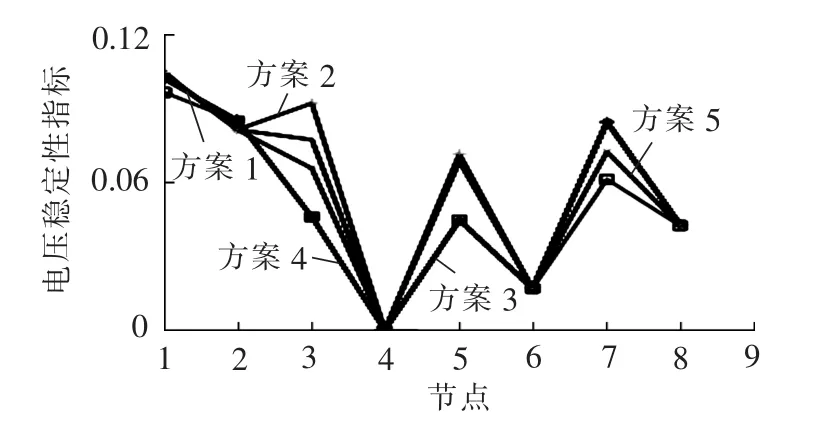
图12 5种方案电压稳定性指标对比图Fig.12 Comparison of voltage stability index among five schemes

图13为5种方案中各条支路的网损情况，5种方案中系统的总网损分别为0.425MW、0.363MW、0.281 MW、0.357 MW、0.298 MW。可以看出，方案2、3、5中线路升级后，减小了支路阻抗，降低了线路1-2的网损，方案1与方案2相比，线路1-2的网损减少量为0.17MW。综合5种方案，DG接入的容量越大，则系统减少的网损越多，总体而言，这5种方案效果相当。

由FMW得到的4种方案，各有侧重，是基于不同角度得到的最优策略，较传统决策手段得到了更多的可行方案。用DEMPSO算法进行优化后得到Pareto非支配集，依据需求规划方的不同侧重点，应用FMW可以快速地得到不同偏好信息下的最优方案，多权重衡量方案的优劣，具有搜索范围广、选择更合理等优点。

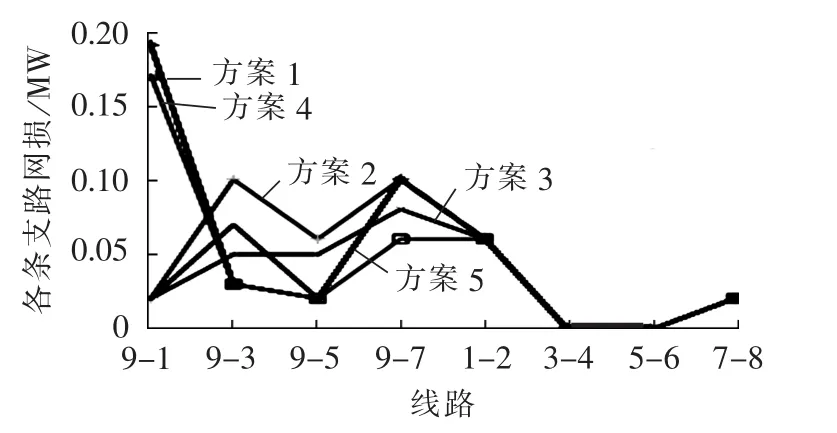
图13 5种方案支路网损对比图Fig.13 Comparison of branch power loss among five schemes

5 结论

本文研究了配电网规划中DG的选址优化问题，可从研究过程及结果中得出如下结论。

a.本文提出的DEMPSO算法可以较好地解决DG优化选址问题，对约束条件的处理更加灵活。本文提出的FMW技术，能够合理地处理主观因素对客观优化问题带来的影响。

b.本文首次从费用、网损、电压指标3个角度独立地进行DG优化选址问题建模，立足于电力系统角度，基于电力系统运行的基本要求，涵盖了可靠性、经济性、电能质量三方面因素，形成了一个考虑因素多、涵盖面广、通用性强的数学模型。

c.以燃气轮机作为DG类型，进行案例分析，结果可知，配电网中接入DG后，改善了系统运行状况，有利于减小系统网损，对节点电压起支撑作用，增强了线路的电压稳定性。综合考虑可知，系统中接入一定数量的DG，会带来诸多效益，这种配置优于传统的配电网线路升级或变电站扩容。