基于LCC的配电网电压偏差治理措施的优化

杨 洁，刘开培，龚汉阳，乐 健

（武汉大学 电气工程学院，湖北 武汉 430072）

0 引言

随着建设社会主义新农村工作的深入展开、家电下乡政策的进一步落实以及我国城市化水平的不断提升，城乡居民用户对于供电质量的要求也逐步提高。但由于历史原因，我国配电系统建设相对发电、输变电系统较为落后，“重发轻供不管用”的问题仍然存在，导致城市及农村配电网电能质量差、供电可靠性低等问题较为突出，其中尤以配电网电压偏差最为严重，危害最大。因此，如何在有限的投资约束下提高投资的效率，尽可能解决配电网现阶段以及中远期的电压偏差问题，已经成为当前的研究热点和电力运行部门实际生产过程中亟待解决的关键问题[1-2]。

目前常用的配电网供电电压偏差改善措施主要有以下几种。

a.无功补偿技术，以并联电容器应用最为普遍。

b.合理选择导线截面。导线截面过小，成本固然降低，但线损增大，易发生电压偏差过大的问题。

c.串联电压补偿技术。该方式可靠性高、响应速度快，但价格较为昂贵，不适合大规模推广应用。

d.调整变压器分接头。该方法投入最小，但一般难以兼顾最大、最小负荷时对供电电压的需求。

e.缩短供电半径。此方式适用于供电半径较长的馈线，但一般引入已有的电源点将受到地理条件的限制，而新增电源点投资相对较大。

现阶段电力企业解决城乡配电网电压偏差问题的方式，大部分仍是凭经验、粗放式的增加设备投资。对于方案的效果以及经济性，却少有系统化、精细化的评估，更多的只是根据设备成本及人工成本大致估算出的预算。该方式显然忽略了环境、经济、日常维护等多种因素造成的追加投资。目前国内鲜有文献对该问题进行过深入研究。国外由于配电网架稳定可靠等原因，更是少有研究对该问题进行深入探讨。

电力设备全寿命周期成本（LCC）是指电力设备从设计到退役的整个期间需要的费用总和，它往往数倍于设备购置费用。LCC具有如下显著特点：费用并不只是发生在投资初期，而是按时序发生在整个寿命周期内。对于配网电压偏差改善方案这个特定对象，采用全寿命周期理论可以有效评估其总体费用，分析费用在寿命周期中的分布，并以此为依据制定相关优化措施。

本文以LCC理论为基础，提出一种配电网电压偏差治理措施的优化方法。首先介绍该方法的流程，根据LCC理论构建配电网改造的成本分解模型，利用统计数据构建常用电压偏差改善措施的LCC费用计算模型。最后以某10 kV馈线为例，根据本文提出的策略，对其电压偏差情况进行了仿真评估，根据各种改造措施的LCC，制定出了优化的电压偏差改善措施方案。

1 治理措施优化方法的流程

本文提出的基于LCC的电压偏差治理措施优化方法的流程如图1所示。

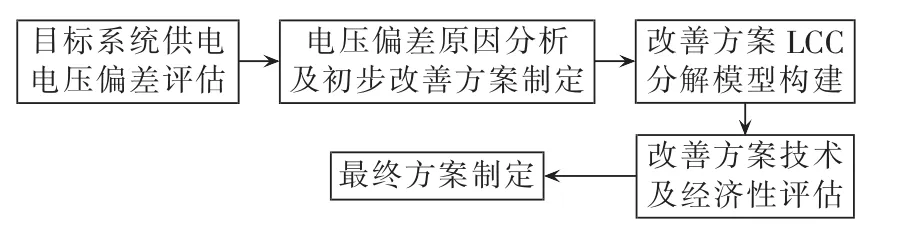
图1 本文所提电压偏差治理流程Fig.1 Flowchart of proposed method for voltage deviation management

该方法主要包括如下几个步骤：

a.根据目标系统接线方式、运行方式、设备参数、负荷情况等信息，利用PSCAD仿真软件进行仿真计算，评估目标系统各负荷点电压偏差情况；

b.根据评估结果，分析造成目标系统电压偏差的主要原因，根据常用改善措施制定治理方案，再次利用仿真计算分析各种治理措施的技术可行性和合理性；

c.根据LCC理论，构建各技术可行治理方案的LCC分解计算模型，以此为基础对各治理方案进行经济性评估；

d.根据技术性和经济性综合性评估结果，制定出目标系统电压偏差治理的优化方案。

2 配电工程改造的LCC分解模型

图2为应用于配电网工程改造的LCC分解模 型[3-6]。

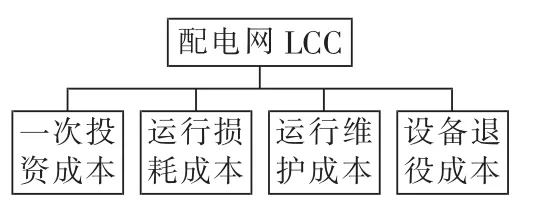
图2 LCC分解模型Fig.2 LCC decomposition model

总的LCC可分解为：

其中，CI为一次投资资本，主要指设备的购买与安装费用；CO为运行损耗成本，对不同的设备有所不同，对于导线而言包括电阻损耗以及电晕损耗，而对于基础设施，则不存在损耗问题；CM为运行维护成本，包含设备的日常维护、维修费用；CD为退役成本，包含设备的退役施工以及残值回收，部分设备不存在残值回收。

2.1 一次投资成本

一次投资成本包括各种设备购买和安装过程中涉及到的各种费用[7-10]。配电网一次设备投资主要包括：配电变压器、电杆及其配件、导线等。对于某个配电网工程改造，一次投资成本的计算公式为：

其中，n为新增或更换变压器的数量，m为需要增设电杆的工程数量，h为新增线路的条数，z为新增电容器的台数；S对于变压器为新增的或更换的变压器容量，对于电杆为其数量，对于导线为其长度，对于电容器为其容量；下标T、P、L、C分别代表配电变压器、电杆、裸导线/绝缘导线、电容器；P为设备单价；A为某对象由于附件购置而需要在该对象原值上增加的百分比，对不同设备有所不同，即使是同类设备，安装方式不同该值也有所区别，例如，杆上配电变压器与墙上安装的费用有所差异；D为施工难度系数，主要与地形或所处区域特征有关，如城市还是农村，平原还是山区。参考配电线路典型设计中的取值，常用配电设备成本如表1所示，施工难度系数如表2所示。

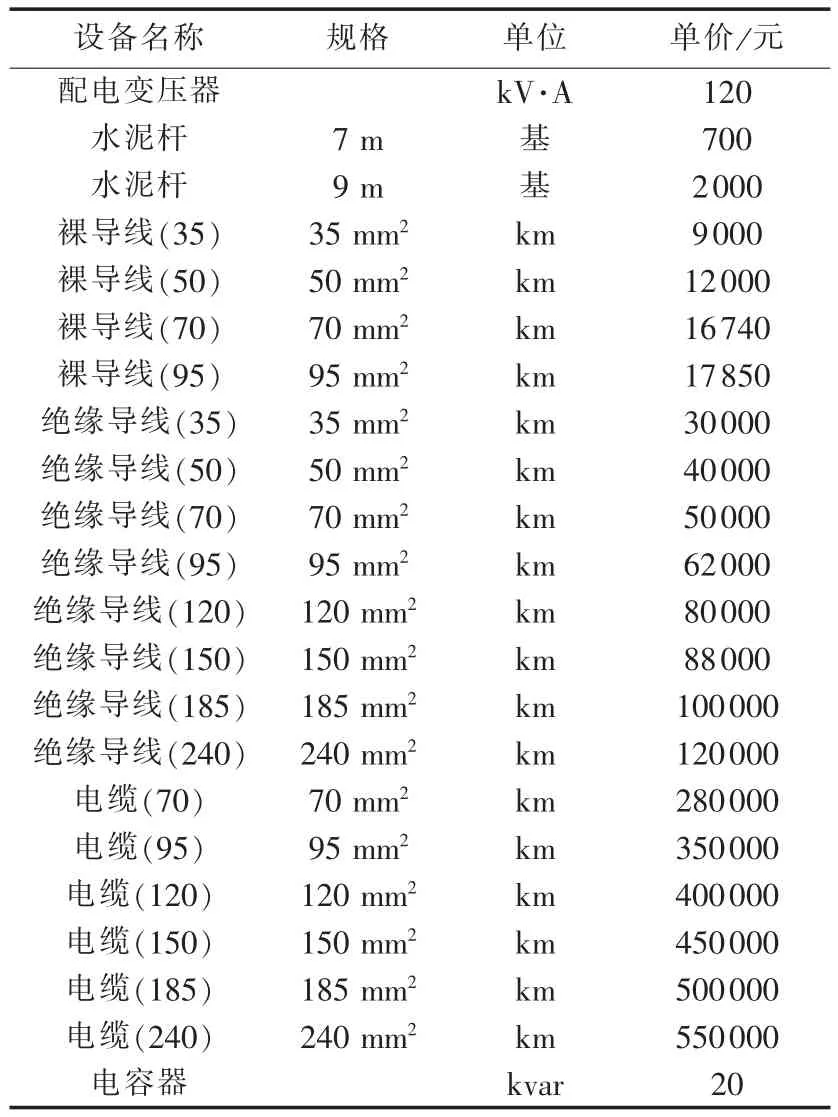
表1 典型配电设备购置成本Tab.1 Typical purchase cost of distribution devices

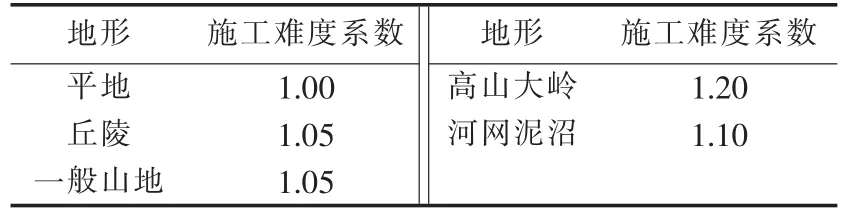
表2 施工难度系数Tab.2 Difficulty degree of project implementation

2.2 运行损耗成本

运行损耗对于配电网而言主要是线损，主要采用基于潮流的网损快速分析计算[11-17]。当采用直角坐标时，依据潮流方程，某一时刻的线损能表达成电力系统状态变量x（电压实部和虚部构成的列向量）的二次型。对应某一潮流状态x0，线损功率可表达为：

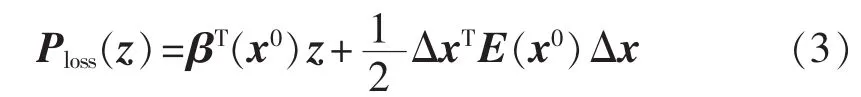
其中，β（x0）为 z0下线损对因变量的灵敏度向量，β（x0）=为误差矩阵，该矩阵仅与电网结构以及初始潮流因变量矩阵z0（节点注入）有关；Δx为状态变量的偏差向量，Δx=x-x0，由保留非线性潮流计算概念，有等式 z-z（x0）=JΔx+z（Δx）的关系，当 Δx非常小时，若忽略二阶项 z（Δx），且 Δz=z-z（x0）已知时，也可根据Δz=JΔx这一近似快速求解Δx。

根据式（3），对应节点注入量z0的潮流状态x0，线损即为 Ploss（z）=βT（x0）x0，也确定了 β=β（x0）的向量以及误差矩阵E=E（x0）。当电网结构不变时，在相同运行方式期间，对应任何情形下的因变量z，以及与初始因变量z0的偏差项Δz=z-z（x0），由直角坐标下潮流计算方程可知：

其中，J为对应x=x0时的雅可比矩阵。

因此在x0下，对应因变量z的变化，通过式（4）迭代，可快速求出系统状态的变化。当然，考虑到系统正常运行情况下，因变量变化引起状态量的变化并不显著，即 Δx很小和 z（Δx）≈0，则也可由 Δz直接根据式（5）求得Δx，也不会引起大的误差。

因此通过某一状态的潮流，因变量的任何变化，都可准确或近似地计算对应因变量变化的线损功率。

2.3 运行维护成本

运行维护费用涵盖的范围较广，主要包括以下几个部分：运行维护人员的工资；运行维护的工具费用；备品、备件的管理和维护费用；车辆及办公费用；故障抢修费用。

由于目前财务管理的精密程度无法达到LCC分析的要求，因此，将所有的维护费用进行均摊，得到大致维护费用如下：

其中，CMt为某一电压等级配电网每年的运行维护费用；lt为该电压等级配电网线路的总长度；t为电压等级。在计算中，需要按照电压等级进行均摊及计算。

2.4 退役成本

退役成本在目前的管理中往往受到忽视。考虑到配电网的实际情况，配电变压器、电杆及裸导线/绝缘导线在一定条件下可以回收其价值。退役成本的计算公式为：

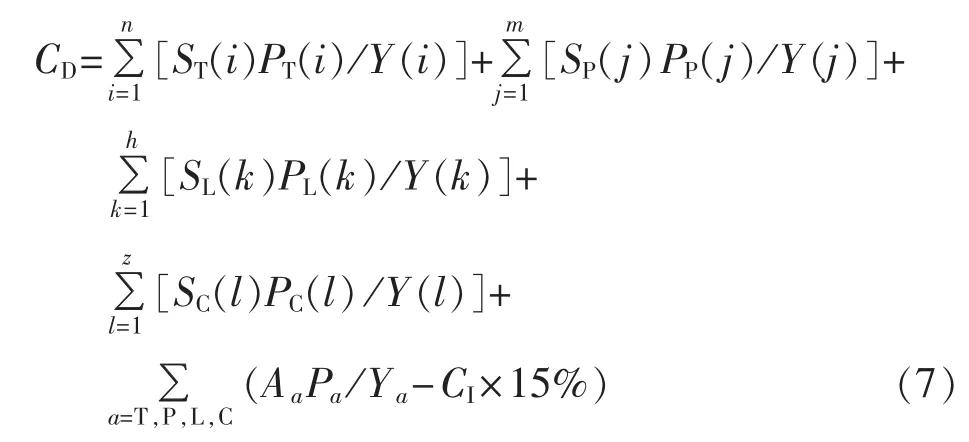
其中，Ya为各设备的平均使用寿命。

需要说明的是：由于电杆、电线、配变、电容器等均可二次回收利用，但必须是完整的才引入计算，并且随着使用年份的增加呈递减趋势计算其价值；附件同样按照运行年份计算其残值；拆除工程的施工费用与正式施工的费用设定为相同。

3 电压偏差改善措施的成本分解模型构建

由于串联电压补偿设备较为昂贵且适用范围小，而重新规划电源点、缩短供电半径较为复杂且花费大，因此城乡配电网电压偏差治理措施主要采用并联电容器、合理选择导线截面以及调节变压器分接头。

根据第2节的LCC分解模型，对以上3种改善措施的LCC模型进行分解计算。

3.1 采用并联电容器的成本计算

对于10 kV线路，可采用并联电容器进行无功补偿，通过降低无功电流来提高供电电压。但一般情况下，无功补偿电容宜安装于台区低压侧进行集中补偿，或者安装于某个功率因数较低的用户处进行就地补偿。

其一次投资成本为：

其中，SC为并联电容器容量（kvar）；取单价 20 元/kvar。

运行损耗成本：并联电容器正常运行过程中仅存在很小的有功损耗，因此对并联电容补偿方法而言可取为0。

运行维护成本：不单独计算，对并联电容器取为0。

退役成本：取一次投资成本的2%。

3.2 更换导线截面的成本模型

一次投资成本为：

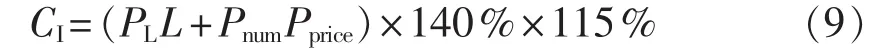
其中，L为更换的导线长度（km），PL为导线的单价（元/km）；Pnum和 Pprice分别为需更换的电杆数量（基）和单价（元/基）；140%和115%分别为计入附件投资和施工费用的系数。

运行损耗成本：由于馈线结构复杂且负荷波动性较大，准确计算出线路损耗非常困难且不必要。本文采用以下简化计算方法计算起始年运行成本：

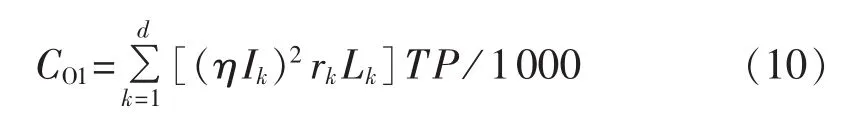
其中，d为全部更换的导线总段数；Ik为由第k段导线后全部配变额定容量和额定电压计算得到的该段导线的额定电流（A）；η为线路平均负载率；rk为第k段导线的电阻率（Ω/km）；Lk为第k段导线的长度（km）；T为每年的总小时数（h）；P为单位有功电价（元/（kW·h））。计算时需考虑年通货膨胀率和贷款利率，对各年运行成本进行等年值折算。按服役年限20 a计算，平均年通货膨胀率为3%，年利率为7%，电费为 0.3元/（kW·h）。总运行损耗成本计算公式为：

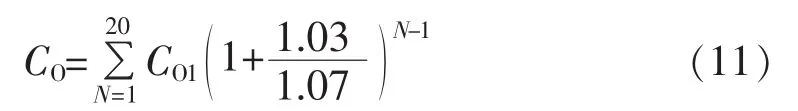
运行维护成本：运行维护成本采用经验公式，即10 kV馈线每km的年平均维护成本为3000元。起始年的全寿命周期计算得到的运行维护成本为：

总运行维护成本同样需要将以后各年的运行维护成本根据上述方法进行等年值折算后相加。

退役成本：取一次投资成本的2%。

3.3 调节变压器分接头的成本模型

对于改变变压器分接头而言，基本不存在新增投资的问题，可能带来的主要损失是将增加变压器的维护成本，本项目未对该方案进行LCC的分析，认为其成本基本为0。

4 应用实例

4.1 目标系统概况

本文的应用对象为某地35kV变电站的1条10kV馈线，其接线如图3所示。

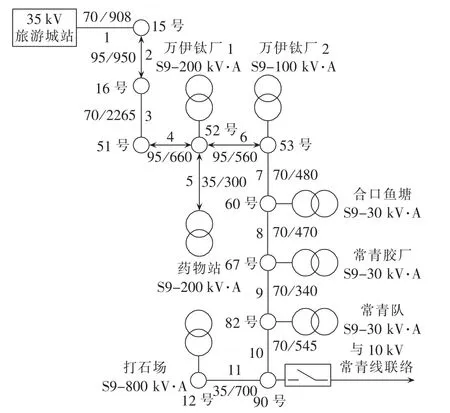
图3 10 kV馈线接线图Fig.3 Connection diagram of a 10 kV feeder

该10 kV馈线共有11段架空线路，各条线路类型及其长度如表3所示。线路负荷、各负荷变压器类型、容量及负载率如表4所示。

4.2 目标系统电压偏差评估及结果分析

首先采用PSCAD仿真软件，通过仿真计算得到该10 kV馈线在额定负荷以及正常负载率情况下的电压偏差情况，结果如表5所示。可以看出，该馈线电压偏差问题随着线路的延伸而不断恶化，线路最末端的打石场供电电压偏差情况最为严重。

表3 10 kV馈线线路参数Tab.3 Line parameters of a 10 kV feeder

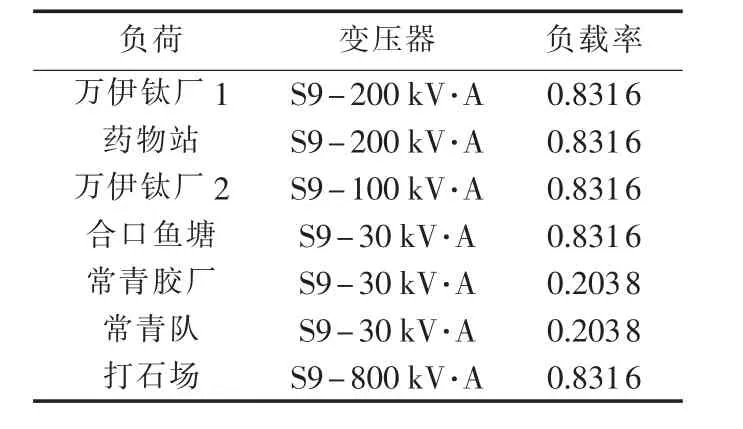
表4 10 kV馈线各负荷统计Tab.4 Loads of a 10 kV feeder

表5 南林线电压偏差评估结果Tab.5 Evaluated voltage deviation of Nanlin line

通过分析该线路的线路分布及负荷情况，可知造成供电电压偏差的主要原因包括：变电站离负荷点偏远，供电半径较大，线路偏长；万伊钛厂、打石场等负荷较重。

4.3 初步改造方案及其技术性评估

根据电压偏差评估结果及原因分析，结合其自身线路、负荷情况，本文为其制定3种改造方案。方案1是将该馈线所有主干线路换成LGJ-150导线，以减小线路电压损耗；方案2是采取集中补偿的方式，增设0.3 Mvar的无功设备；方案3是将馈线入口变压器分接头的档位上调一级。

利用PSCAD软件对以上3种改善方案展开技术性评估，电压偏差改善结果如表6所示。可以看出，方案1对于解决电压偏差问题效果最佳，方案2次之，方案3最差。

4.4 各改造方案经济性评估

结合3节中各改造方案的成本分解模型，对基于LCC的各种方案进行经济性评估[18-19]，结果见表7（由3.3节可知，方案3成本为0，故未在表中示出）。可看出方案1较方案2和方案3的花费巨大。从经济性角度而言，方案3最好，方案2次之，方案1最差。

表6 南林线电压偏差治理方案Tab.6 Schemes of voltage deviation management for Nanlin line

表7 电压偏差治理方案的LCC比较Tab.7 Comparison of LCC among voltage deviation management schemes 万元

4.5 治理方案的优化

根据技术性和经济性分析结果，最终得出了该10 kV馈线适用的电压偏差改善措施及其排序：以方案3的经济性及技术性最为适中，宜优先选取；方案1的技术性最好，而经济性最差，但方案1在改善电压偏差的同时也有提高线路供电可靠性等其他效果，因此宜将经济条件与供电可靠性、电压偏差结合考虑，以决定选择主线换径或者无功补偿。

最终，该10 kV馈线电压偏差治理的方案确定为优先选择变压器分接头档位上调一级，并在变压器二次侧加设无功补偿电容器。

5 结论

本文以LCC理论为基础，提出一套治理配电网电压偏差的优化方法。该方法首先确定出技术性可行的电压偏差治理方案；其次基于LCC理论，计算得出各治理方案的LCC，并进行经济性评估；最终根据技术性和经济性分析确定出最为合理的电压偏差治理方案。以某10 kV馈线为例，说明了该方法的具体实现。本文方法的原理简单，方案制定兼顾了技术性和经济性，为提高供电部门制定配电网改造方案的科学性和经济性提供了可靠的决策依据。