微电网分层分布式能量优化管理

郝雨辰，窦晓波，吴在军，胡敏强，孙纯军，李 桃，赵 波

（1.东南大学 电气工程学院，江苏 南京 210096；2.江苏省电力设计院，江苏 南京 211102；3.浙江省电力试验研究院，浙江 杭州 310014）

0 引言

将分布式电源和负荷以微电网的形式组合起来，通过合理改变各类电源的工作状态，进行必要的负荷控制，能够减小系统环境污染，改善客户用电可靠性，提高能源利用经济效益，从而实现微电网的能量优化管理，这不仅是微电网系统不同于大电网的特殊性，也是微电网领域研究的重点与难点[1]。

由于微电源的功耗特性不同于传统电网中的同步发电机，因此等微增率原则不再适用于微电网能量优化管理[2]。 文献[3-5]针对系统的经济性、环保性和供电可靠性，建立了并/离网状态下微电网能量管理模型，但设计的优化策略依赖于中心控制器的性能，不能充分体现不同微电源的运行特性甚至无法反映同类微电源的不同控制目标。文献[6-9]采用线性加权法、模糊优化法、小生境进化法、2层规划法对微电网能量管理的多目标优化问题进行了阐述。文献[10-11]从微电网结构特点出发，提出了层次化的微电网控制与能量管理思想，但实现手段还是传统的主从控制策略，缺乏层间的协作与互动。文献[12-14]将多代理（Agent）系统方法用于微电网能量调度中，描述了各Agent的任务并构建了多Agent系统平台，但缺乏针对不同优化问题尤其是多目标优化问题，采用不同方法的分层分布式应对机制的阐述。

本文以提高系统经济性、环保性和供电可靠性为优化目标，设计了并网微电网能量管理模型和相应的多Agent系统框架，针对系统单目标和多目标优化问题，基于Agent的自治性与协作性，提出了分层分布式的优化管理策略，通过MATLAB和JADE平台构建针对未来24 h的系统优化算例验证所提方法的正确性和有效性。

1 微电网能量优化管理模型

1.1 微电网模型

本文建立的微电网系统由光伏PV（PhotoVoltaic）电池、风力发电机WT（Wind Turbine）、微型燃气轮机MT（Micro Turbine）、2组质子交换膜燃料电池PEMFC（Proton Exchange Membrane Fuel Cell）和蓄电池等分布式微电源组成，并通过联络线与配电网相连接，其系统结构及单元间的分层分布式关系如图1所示。

为了体现本文提出的微电网分层分布式能量优化管理策略能够突出不同单元运行特性和控制目标的优点，设定：系统中MT和A组PEMFC工作在高效率区间；B组PEMFC输出功率尽可能小，由于

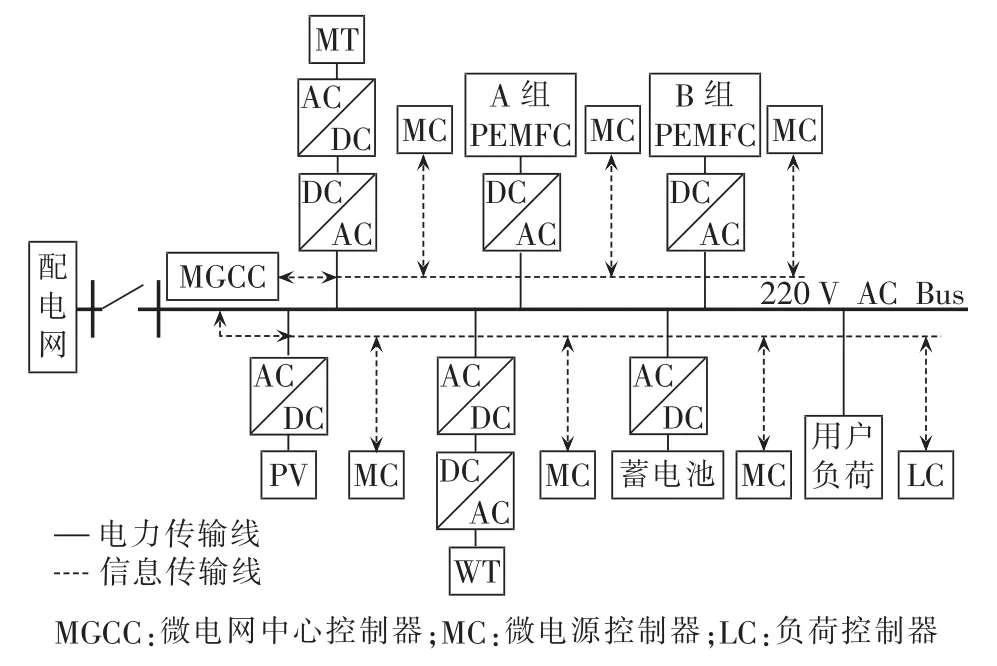
图1 微电网模型结构图Fig.1 Structure of microgrid model

PEMFC具有低温下迅速启动的优点[15]，因此使其只在系统负荷较大时作为备用电源启动。

1.2 目标函数

由于可再生能源发电享受优先调度权和电量被全额收购的优惠[4]，因此本文微电网能量管理的对象是MT、PEMFC、蓄电池等可控单元。分别针对系统经济性、环保性和供电可靠性定义相应目标函数。

1.2.1 微电网的经济性

微电网的经济性可定义为包含耗能电源的燃料成本、各单元的管理成本以及与配电网间功率交换的购电成本或售电收益等费用的总和，如式（1）所示。

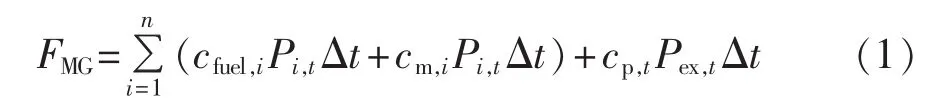
其中，n 为微电源数量；Pi，t为微电源输出功率；cfuel，i和cm，i分别为各微电源燃料成本与管理费用；cp，t为t时刻配电网实时电价；Pex，t为配电网与微电网间交换功率，功率注入微电网为正，反之为负。由于蓄电池只考虑管理费用，因此，Pi，t表示其充放电功率时，需取绝对值。

1.2.2 微电网的环保性

微电网的环保性可定义为系统内微电源输出功率以及配电网注入功率造成污染气体的排放，由此带来的污染气体治理费用的总和如式（2）所示。

其中，m为本文考虑的污染气体类型数量，fi，j、fj和cj分别为第i个微电源或配电网产生的第j类污染气体的排放系数与相应治污成本，如表 1所示[4，16]。

表1 污染气体排放系数与治污成本Tab.1 Pollution gas emission coefficient and control costs

1.2.3 微电网的可靠性

文献[17]中以功率供给亏欠率作为微电网供电可靠性指标，本文在此基础上基于实时电价信息，综合文献[18]提出的分级切负荷思想、文献[19]提出的高赔偿可中断负荷的概念，以对停运负荷的补偿费用作为衡量系统供电可靠性的标准，如式（3）所示。

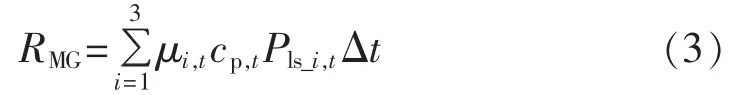
其中，μi，t为t时刻各类型负荷相对实时电价赔偿系数；Pls_i，t为切除某类负荷的大小。

1.3 约束条件

将微电源的不同运行特性和操作人员的控制目标作为约束条件并入微电网能量优化管理模型中。

由于合理的切负荷操作比全负荷供电具有更高的经济效益[20]，因此本文允许进行切负荷操作，但需满足功率平衡约束式（4）和负荷削减量约束式（5）。

其中，PLoad，t和 Pls，t分别为 t时刻负荷预测量和负荷削减量的大小；εls，t为t时刻负荷削减量与负荷预测量的比值，εlsmax为该比值的最大设定量。

并网状态下，微电网与配电网间的交换功率具有双向最大值约束，如式（6）所示。

由于本文只考虑电负荷需求，不考虑MT的热电联供效应，因此，作为输出功率可控的MT和PEMFC，其约束条件主要包括输出功率上、下限约束和单位时间输出功率变化率约束，分别如式（7）、（8）所示。

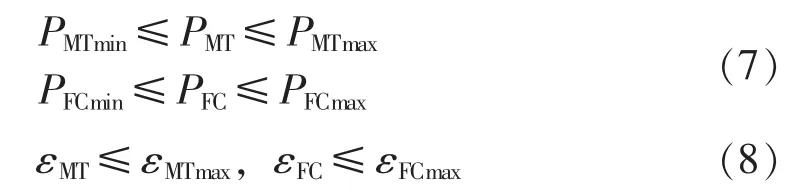
由于B组PEMFC只在负荷较大时作为备用电源使用，优化计算中对其不考虑式（8）所示约束条件。

蓄电池是微电网中价格较高的单元，因此，合适的约束条件和合理的控制参数对于改善蓄电池的使用寿命具有重要作用。

a.充放电深度约束：合理的工作区间有利于延长蓄电池使用寿命和提高工作效率[21]，因此，其荷电状态 SOC（State Of Charge）约束如式（9）所示。

b.充放电功率约束：蓄电池单位时间充放电功率ΔPBat受其物理性质制约，根据文献[22]所述，限定其在a中所述SOC工作区间内的充放电功率和蓄电池额定容量CBat的关系如式（10）所示。

c.充放电转换次数约束：充放电深度决定了蓄电池循环总次数[23]，即使用寿命。通过限制其每天充放电转换次数TBat以延长工作时间，如式（11）所示。

d.状态一致性约束：每天00:00与24:00时蓄电池的荷电状态需保持一致，如式（12）所示。

a—d中，下标max和min表示变量的上、下限。

综上所述，本文中微电网能量优化管理的目标，即为根据PV、WT和系统电负荷的预测信息，在满足式（4）—（12）所示约束条件的基础上，采用提出的分层分布式优化策略，制定未来24 h每时刻各单元的调度计划，使得式（1）—（3）单独定义或组合表示的系统单目标或多目标优化的目标函数取得最小值，即为微电网经济性、环保性和可靠性的最优解。

2 微电网分层分布式能量优化策略

不同于广泛采用的集中式优化策略，本文根据微电网的结构特点，以式（1）—（3）最小化为优化目标，采用遗传算法作为计算方法，TCP/IP协议作为通信手段，依靠微电网中心控制器MGCC（MicroGrid Central Controller）、微电源控制器 MC（Microsource Controller）、负荷控制器 LC（Load Controller）间的相互协作，分别针对系统单目标与多目标优化问题，设计相应的微电网分层分布式能量优化策略。

2.1 单目标优化策略

针对微电网系统能量管理的单目标优化问题，设计了2种分层分布式的优化策略，如图2所示。

由图2可知，本文提出的分层分布式能量优化管理策略包含以下4个阶段。

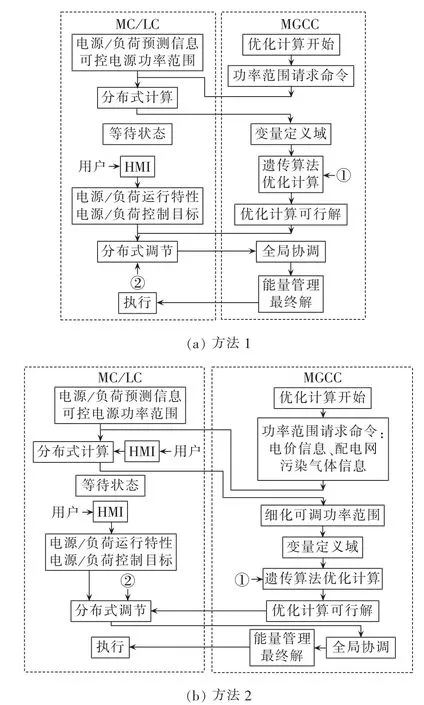
图2 分层分布式优化策略Fig.2 Hierarchical and distributed optimization method

阶段1：微电源分布式计算。各MC将控制单元可调功率范围信息上传给MGCC，2种方法区别在于方法1中各单元可调功率范围仅与其额定功率有关，而方法2中还考虑到了用户对于所控单元未来24 h运行目标的控制指令，因此方法2上传信息是方法1上传信息的子区间。除此之外针对不同优化目标，方法2还将各单元发电成本、污染气体排放系数等预测信息一并上传，由MGCC根据反馈结果，并参照LC发布的预测信息细化式（6）、（7）的约束条件。

阶段2：MGCC优化。MGCC根据各微电源输出功率可调范围信息，在切负荷操作允许范围之内，考虑式（4）—（7）、（10）所示约束条件（图 2 中以①表示），采用遗传算法得到优化计算可行解，并将此解传递给各MC。

阶段3：分布式并行调节。MC基于自身运行特性和用户指令要求，定义式（8）、（9）、（11）、（12）所示约束条件（图2中以②表示），完成对可行解的修改工作，并将修改后的可行解和MC所能接受的调节范围一并上传给MGCC。

阶段4：生成最终解的全局协调。MGCC以MC反馈结果为基础，将配电网视为平衡机组，在不超过Pexmax的条件下生成最终解。如出现交换功率越限的情况，则根据MC发电成本或污染排放等信息，采用MC反馈信息中包含的可接受的调节范围进行微调。

综上所述，MGCC采用遗传算法进行优化计算过程中，只考虑了部分约束条件，因此相对于传统集中优化而言，具有较快的运算速度，之后MC的调节过程属于并行计算，具有很高的计算效率。

以方法2为例，针对不同的优化目标，介绍相应的分层分布式优化方法。

2.1.1 微电网经济性优化

在分布式计算阶段，MC根据用户控制要求，计算各单元运行区间以及相应的最高与最低运行成本，并与MGCC发送的实时电价信息进行比较，将比较结果与工作区间反馈给MGCC，MGCC基于此反馈信息和负荷预测值，根据图3所示流程图和表2所列管理方案，细化各电源的可调功率范围信息。图3中 cFCmax、cFCmin和 cMTmax、cMTmin分别为 PEMFC 和 MT 的最高运行成本与最低运行成本。从本文第3节的介绍中可知，上述 4 个变量具有 cMTmax＞cMTmin＞cFCmax＞cFCmin的数学关系。

对于蓄电池充放电管理除了表2中明确表示的方案A中充电、方案E中放电，其他情况下蓄电池可充可放。B组PEMFC启动原则在2.1.2节中介绍。

在分布式调节阶段，MC参照优化计算可行解中各时刻输出功率间的变化关系，根据约束条件的限定要求修改此可行解，修改后的解不仅完全体现各单元的运行特性和用户的控制要求，而且与可行解具有一致的变化规律，在某些时刻甚至完全一致。

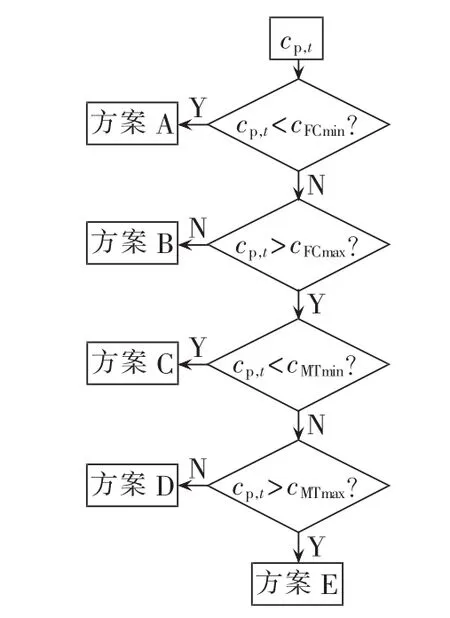
图3 MGCC经济性优化流程图Fig.3 Flowchart of economical optimization for MGCC

表2 MGCC经济性优化管理方案Tab.2 Scheme of economical optimization management for MGCC

2.1.2 微电网环保性优化

在分布式计算过程中，MC将各单元与配电网间污染气体排放的比较信息，以及用户设定的工作区间上传给MGCC，从表1可知PEMFC环保效益最高，其次是MT，因此MGCC按图4所示流程图以及表3所列应对方案细化各单元可调功率范围信息。图4中PFCAmax和PFCAmin分别为A组PEMFC功率调节范围的上、下限。

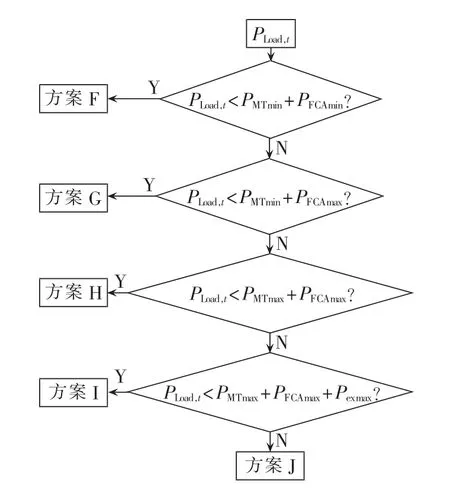
图4 MGCC环保性优化流程图Fig.4 Flowchart of environmental optimization for MGCC

表3 MGCC环保性优化管理方案Tab.3 Scheme of environmental optimization management for MGCC

不同于微电网经济性优化，环保性优化过程中各电源污染气体排放情况不随时间变化，并且蓄电池能量也是通过充电过程获得，所以蓄电池只有在交换功率为负时充电、为正时放电才能起到改善系统环保性的作用。为了减小蓄电池的充放电次数延长其使用寿命，在环保性优化中，蓄电池只在方案F中充电，方案J中放电，其余时刻不充不放。

当MT、A组PEMFC和交换功率最大值总和小于t时刻负荷值时，即为B组PEMFC启动条件定义的系统负荷较大时，如图4所示。B组PEMFC启动原则适用于本文所有单目标、多目标优化计算。

MC的分布式调节只与微电源运行特性和用户预期控制目标有关，与系统级优化目标无关，因此微电网环保性优化的分布式调节与经济性优化一致。

2.1.3 微电网可靠性优化

不同于经济性和环保性优化，微电网可靠性优化的分布式计算阶段，MC仅需将各单元的可调功率范围直接上传给MGCC，而MGCC也无需进行任何处理，直接以此范围作为遗传算法变量的定义域。

可靠性优化的分布式调节阶段与上述2种优化的分布式调节过程完全一致。

2.2 多目标优化策略

采用传统单目标加权法处理多目标优化问题时，权重系数对求解结果影响很大，无法得到全局最优的Pareto解集[24]。针对系统经济性、环保性和供电可靠性构成的多目标优化问题，本文基于多目标优化计算得到的Pareto解集，采用下述2种分层分布式的优化策略获取微电网最优能量管理方案。

a.MGCC以系统经济性、环保性作为多目标优化，采用遗传算法求取Pareto解集，再利用供电可靠性作为评价指标，以Pareto解集中可靠性最高解（对应式（3）取最小值）作为多目标优化的最优值。

b.MGCC以微电网经济性、环保性和供电可靠性作为多目标优化，采用遗传算法求取Pareto解集，将此解集传递给各MC，MC以所控单元的运行特性和控制目标定义的约束条件作为评价指标，完成对Pareto解集的评定工作并反馈给MGCC，MGCC综合各MC的反馈信息最终生成多目标优化的最优值。

上述2种多目标优化的程序流程与图2中单目标优化方法2的流程一致。将单目标优化分布式计算所得变量定义域的并集作为遗传算法多目标优化中变量的定义域。对于2种多目标优化方法得到的最优值，采用与单目标优化相同的分布式调节方法。

2.3 遗传算法

MGCC采用遗传算法进行微电网能量管理优化计算，根据各单元输出功率调节范围，以及式（5）表示的允许负荷缺电率大小，随机生成包含100个个体的初始种群，经过500代选择、交叉、变异的迭代计算得到单目标或多目标的优化解。其中选择操作采用个体数为4的锦标赛选择法，交叉操作与变异操作分别采用式（13）和式（14）所述数学方法。

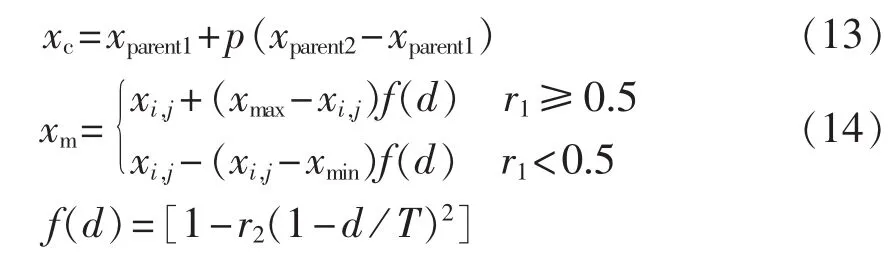
其中，xc、xm分别为交叉与变异操作子个体；xparent1、xparent2为交叉操作父个体；p为交叉率；xi，j为种群中第i个个体的第j个基因；xmax、xmin分别为相应基因的最大、最小值；d为当前迭代次数；T为最大迭代次数；r1、r2均为随机变量。由此可见，本文采用的遗传算法是与迭代代数相关的自适应算法。

初始种群生成与迭代进化过程中，确保种群中每个个体均满足各单元输出功率范围的要求，以及允许切负荷大小的约束，这种进化思想既使得优化解可行，也减轻之后MC分布式并行调节的负担。

3 多Agent系统结构

将多Agent系统方法用于微电网分层分布式能量优化管理中，赋予系统中每个单元Agent的角色，定义各Agent的任务。利用代理的自治性，在优化解的生成过程中，体现了各单元的运行特性和控制目标；利用Agent的协作性，将传统集中优化转为效率更高的分布式并行计算，弱化了对MGCC性能的要求。

基于图1中微电网结构，建立满足图2分层分布式优化策略要求的多Agent系统框架，如图5所示。

图5 多代理系统框架Fig.5 Framework of multi Agent system

从图5中可见，健全的通信网络和完善的Agent通信语言和协议是实现本文提出的优化策略的基础，采用满足FIPA国际标准的Agent通信语言ACL和Contract Net等协议进行交互，并利用TCP/IP协议确保不同层次、不同单元间协作信息的可靠传输。

基于表4所列微电网系统的参数信息，设计各Agent的工作任务。

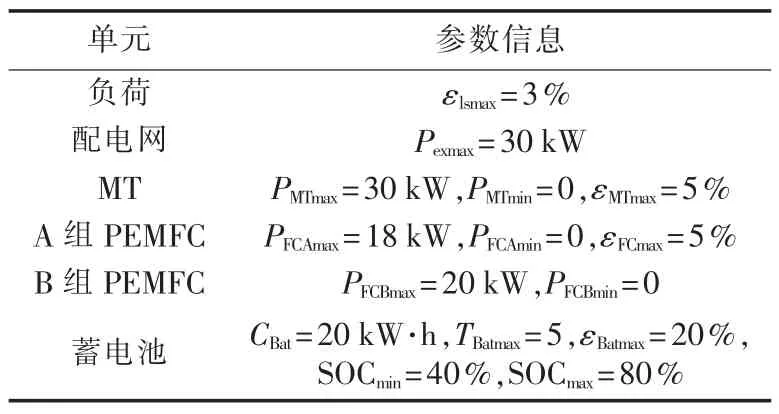
表4 微电网系统主要单元参数信息Tab.4 Parameters of key units in microgrid

a.MGCC Agent：负责与系统中各单元Agent通信，了解各单元的基本信息，采用遗传算法进行优化计算，并根据各微电源Agent的反馈信息进行全局协调，由此形成最终的发电和切负荷计划。

b.PV Agent和WT Agent：根据气象预测信息，将其输出功率预测值上传给MGCC Agent。

c.蓄电池Agent：分布式计算阶段，将蓄电池基本信息和式（10）所示约束条件上传给MGCC Agent；分布式调节阶段，按照式（9）、（11）、（12）所示约束条件修改MGCC优化计算的可行解，并将修改后的值反馈给MGCC Agent；对于多目标优化，蓄电池Agent综合考虑充放电转换次数与充放电功率2个因素，按照式（15）所示评价函数完成对Pareto解集中解的评价工作。

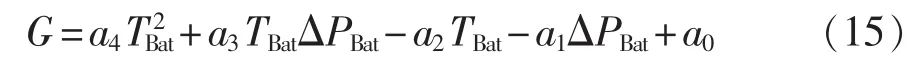
其中，a0—a4取值 1.072、0.082、0.063、2.387× 10-3、8.505×10-4，相应的评价函数曲线如图6所示。

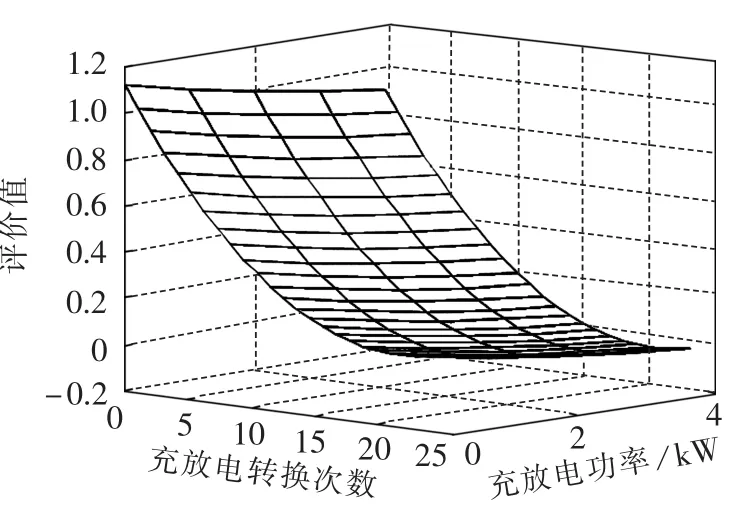
图6 蓄电池综合评价函数曲线Fig.6 Curve of battery comprehensive evaluation function

d.MT Agent：分布式计算阶段，用户根据图 7（a）所示MT效率曲线设定其工作区间，本文设定MT工作效率不低于28.5%，对应输出功率范围为26～30 kW。MT Agent将此调节范围与MT运行成本或污染气体排放情况上传给MGCC Agent。

MT运行成本与其效率有关，因此式（1）中的MT 燃料费用[25]采用式（16）进行运算。

图7 微型燃气轮机和燃料电池效率曲线Fig.7 Efficiency curves of micro-turbine and fuel cell

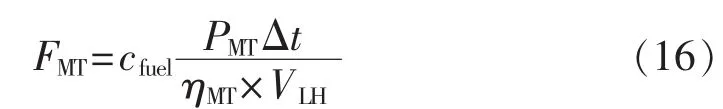
其中，cfuel和VLH分别为天然气单价和低热值，分别取 2.05 元 /m3和 9.7 kW·h /m3；ηMT为 MT 运行效率。

在分布式调节阶段，MT Agent根据输出功率变化率约束式（8）修改MGCC优化计算可行解。

对于多目标优化，MT Agent综合运行效率与输出功率变化率2个因素，按照与图6类似的评价函数曲线完成对Pareto解集的评价工作。

e.A 组 PEMFC Agent：根据图 7（b）所示效率曲线设定其工作效率不低于61%，对应输出功率为7.4～11.2 kW。A组PEMFC Agent的其他任务，如燃料费用计算与多目标评价函数，与MT Agent基本一致。

f.B组PEMFC Agent：利用Agent自治性突出各单元不同特性和控制目标，彰显多Agent系统优点。区别于A组PEMFC任务，B组PEMFC Agent使其尽可能少发电或不工作，仅在负荷较大时参与调节。对于多目标优化，B组PEMFC Agent按照输出功率尽可能小的原则完成对Pareto解集的评价工作。

g.负荷Agent：分层分布式优化计算开始前，将不同类型负荷的预测信息和赔偿系数上传给MGCC Agent；优化计算之后，按时执行最终的切负荷计划。

4 仿真与分析

采用MATLAB作为系统能量优化计算工具，在实验室百兆以太网环境下，利用JADE平台在多台计算机上构建分层分布式的多Agent系统框架。根据图8所示的PV、WT和负荷预测信息，分别针对不同优化目标实现相应的分层分布式能量优化管理。

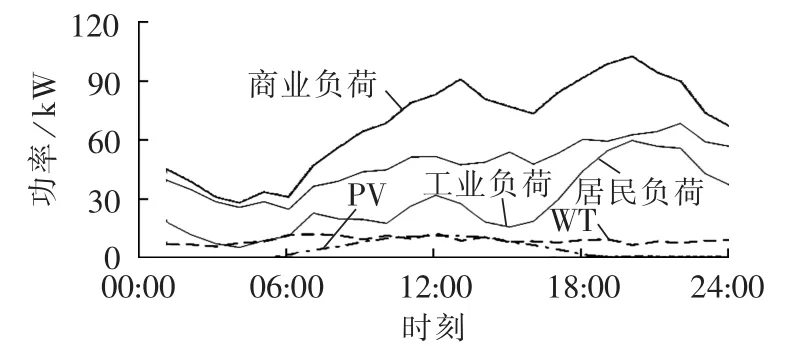
图8 微电网系统功率预测信息Fig.8 Predicted power information of microgrid

4.1 微电网单目标优化

基于微电网能量优化管理模型，针对系统经济性、环保性和供电可靠性的优化目标，采用分层分布式的优化策略和遗传算法进行迭代计算，并与传统集中式的优化结果进行比较，如表5所示。

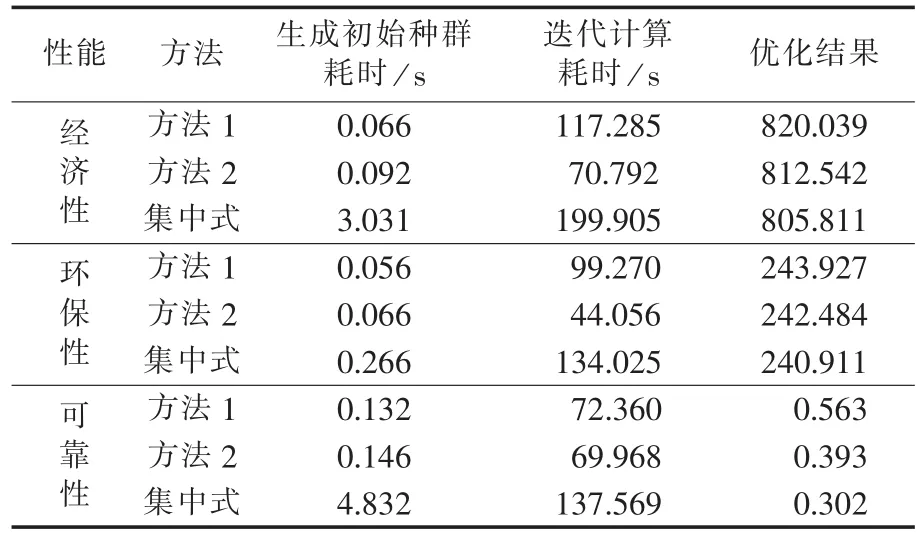
表5 微电网单目标优化结果Tab.5 Results of microgrid single-objective optimization

由表5可见，本文设计的微电网分层分布式能量优化管理策略，由于迭代计算环节并不考虑所有的约束条件，而将部分约束条件在各单元Agent的分布式调节中通过并行计算予以实现，因此，相对于传统集中优化而言，具有更高的运算效率和相近的计算结果。

从表5中不难发现，单目标优化方法1相对于方法2在生成初始种群环节具有更快的速度，但在迭代计算过程中耗时更长，这是因为方法1初始种群中各电源的额定输出功率即为各变量的定义域，而方法2中经过各Agent的分布式计算，各变量的定义域已是考虑了微电源运行特性和用户控制要求的功率区间，因此方法1变量的取值范围更广，更易生成满足式（5）约束的初始种群。而在迭代计算过程中，随着迭代次数的增加，式（14）中 f（d）取值增大，并且变异操作需与该变量的最大、最小值进行减法操作，方法1由于变量取值范围更广，因此变异操作易造成个体中某变量突变，从而不满足式（5）所示的负荷的范围要求，所以方法1在迭代计算环节耗时更长。

上述研究是针对包含4个可控微电源的并网系统，为了进一步说明本文提出的分层分布式能量优化策略相对于传统集中式优化的优越性，在运算参数完全相同的条件下，针对包含40个可控微电源的并网系统的经济性进行优化计算，从表6所列结果中可见所设计的分层分布式策略具有更加显著的运算速度优势，并且优化结果也优于传统集中式优化。

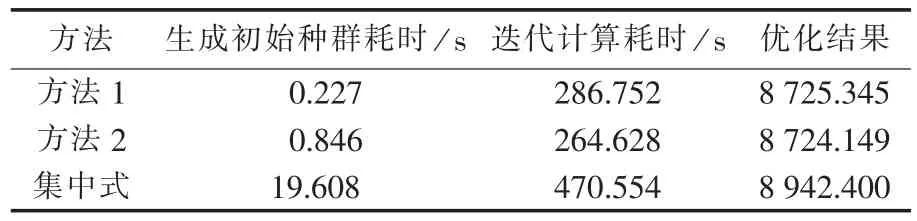
表6 多微电源的微电网经济性优化Tab.6 Economical optimization of microgrid with multiple micro-sources

4.2 微电网多目标优化

分别采用本文提出的2种分层分布式多目标优化方法处理微电网能量管理问题，所得Pareto解集和相应的处理结果分别如表7、8所示。

表7 方法1所得微电网优化Pareto解集Tab.7 Pareto solution obtained by microgrid optimization method 1

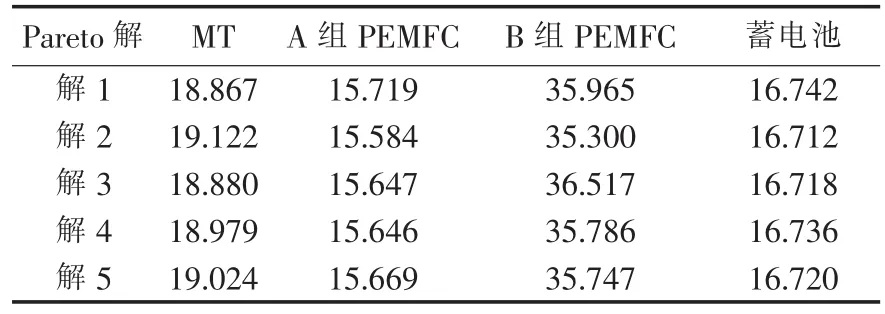
表8 各单元对方法2所得微电网优化Pareto解集的评价值Tab.8 Evaluation of each unit on Pareto solution obtained by microgrid optimization method 2

方法1中MGCC Agent针对微电网经济性和环保性的多目标优化计算后，采用供电可靠性作为评判依据选定Pareto解集中的解1作为优化可行解，对此解经过各微电源Agent的分布式并行调节过程之后，得到最终的电源出力与切负荷计划，此时系统经济性、环保性和供电可靠性指标分别为818.138、249.803、8.643。由于需满足各单元的运行特性和控制目标，因此分布式并行调节后系统各项指标不同于调节前的可行解。

方法2中MGCC Agent针对微电网经济性、环保性和供电可靠性的多目标优化计算后，将Pareto解集传递给各单元Agent进行评价，之后MGCC Agent综合各Agent的评分，选取表8中得分最高的解3作为优化计算的可行解，在经过各Agent的分布式并行调节过程后，最终得到各单元的发电和切负荷计划如图9所示。

本文提出的微电网分层分布式能量优化管理策略，无论针对系统单目标优化还是多目标优化问题，都能得到与图9类似的波形曲线，从中可见分布式并行调节只是各单元Agent对MGCC Agent优化计算可行解的微调，两者具有类似的变化规律，某些时刻甚至完全一致，其优势在于既遵从了MGCC全局优化计算的优化结果，又能更全面地体现各单元的运行特性和控制目标，并具有更高的计算效率。

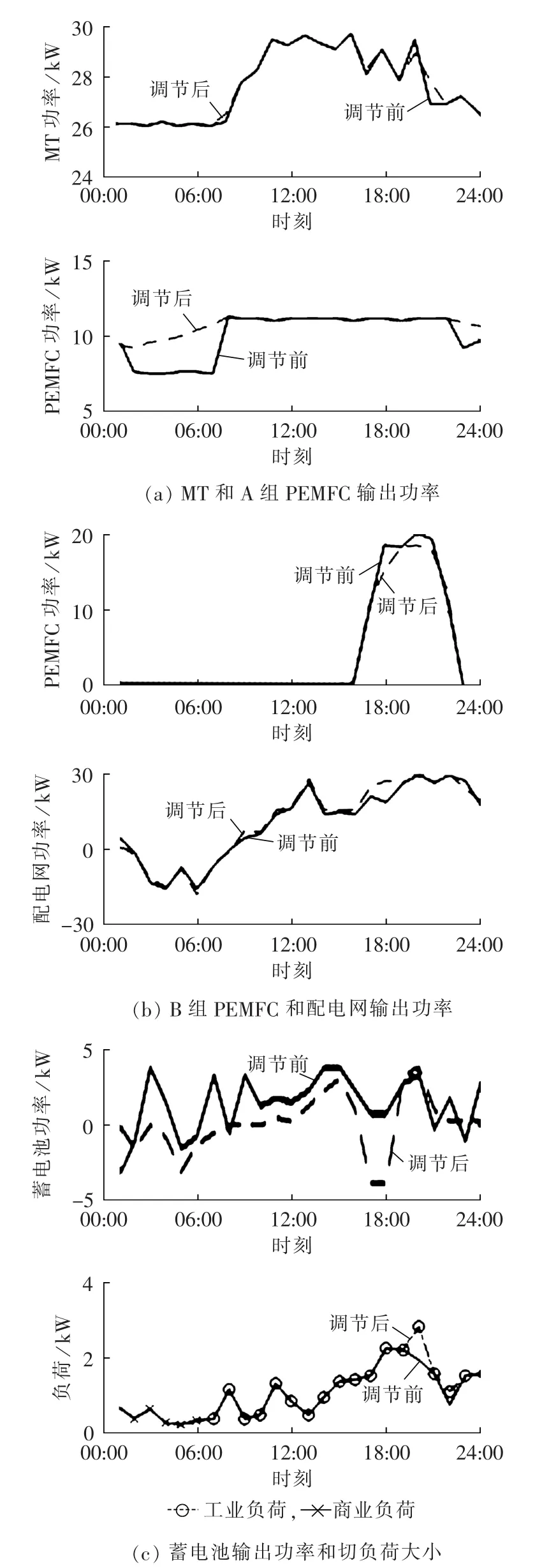
图9 微电网能量管理优化结果Fig.9 Results of microgrid energy management optimization

虽然本文是以预测信息为基础制定未来24 h每时刻各单元的调度计划，但提出的优化策略也适用于基于短期或超短期预测的微电网能量优化，通过在不同时间尺度下取舍分布式交互环节的次数以提高优化速度，例如针对超短期优化可直接忽略图2中MC分布式调节环节中与各单元使用寿命相关的约束条件，而仅保证MGCC优化迭代计算环节与微电源性能相关的约束条件的实现。

5 结论

本文以提高微电网系统经济性、环保性和供电可靠性为目标，建立了微电网能量优化管理模型及相应的多Agent系统框架，采用遗传算法和TCP/IP协议作为技术支持，在百兆以太网的实验环境下，以MATLAB和JADE作为仿真平台建立针对未来24 h的系统优化算例，分别针对系统单目标和多目标优化问题设计了多种分层分布式能量优化管理策略。仿真计算结果表明，相对于传统的集中式优化，本文提出的分层分布式优化策略不仅具有更高的计算效率，并且能更全面地反映不同单元的运行特性和控制目标，特别是在多微电源的微电网能量优化管理中具有更加显著的优势。同时，这种在不同阶段考虑不同约束条件的优化思路，不仅有效地减轻了对MGCC的性能依赖，而且为今后诸如不同时间尺度的微电网能量管理体系的建立也提供了相应的技术支持，因此，本文提出的分层分布式管理策略完全适用于微电网的能量优化管理。