新型永磁风电系统的低电压穿越性能研究

张明锐，黎 娜，王之馨

（同济大学 电子与信息工程学院，上海 201804）

0 引言

大容量并网型风电系统在电网故障情况下的持续运行能力直接影响电网对风电的消纳能力和风电场的经济效益，风电机组的低电压穿越LVRT（Low Voltage Ride Through）能力正是衡量这种持续运行能力的重要指标，其意义在于：电网电压跌落时，风电机组可以通过功率支持帮助电网恢复正常电压而不是脱离电网[1]。因此，对风电系统LVRT能力的研究具有十分重要的工程应用价值。

在实际的电力系统中，三相短路故障发生的概率不大，但造成的后果最严重；单相接地短路和两相短路故障等引起的电网电压不对称跌落，将导致风电系统直流母线产生2次纹波[2-3]，并网电流产生3次谐波[4]，对系统中功率器件造成严重安全威胁。在电网不对称故障下实现LVRT的方法主要有以下几种。

a.采用硬件方式，在并网逆变器交流侧加装带通滤波器，以滤除三相不平衡电压中的负序分量。此方法需要额外的滤波器件，成本较高。

b.改进控制方法[4-5]，有代表性的是在PI控制支路上并联RES控制器（非理想谐振控制器），构成一种新型的PI-RES控制器，实现对2倍频交流信号的稳态无差控制。文献[4]采用3个PI-RES控制器来调节直流电压和瞬时功率，省去了正负序分解与合成计算，减少了计算量，但其控制系统较为复杂。

c.在控制算法上，采用对称分量法，将不对称电压、电流作正负序分解后分别控制[6]。此方法计算量较大，但控制效果好。

综合考虑，风电机组实现LVRT的实用方法是在直流侧增加Crowbar电路，通过快速吸收故障情况下直流母线的不平衡能量来实现。很多文献都采用Crowbar电路实现 LVRT[7-9]，但对电路中储能元件选择、容量计算及具体的控制方法都没有做深入的研究。

本文提出一种基于固态变压器[10-11]结构的永磁风电系统，以超级电容为储能元件构成Crowbar电路，采用同步坐标变换下的正负序电压定向控制策略，实现不对称故障下的LVRT功能，构建了一种全新的具备良好LVRT能力的永磁风电并网系统。

1 风电系统模型及LVRT要求

1.1 新型风电并网系统结构

如图1所示，自然界的清洁风能通过风力机转换成机械能，驱动永磁同步发电机输出电能。发电机定子侧输出的交流电通过PWM整流器转换为低压直流，再通过单相全桥逆变器调制成高频交流，然后通过高频变压器升压，经单相全桥整流器还原为直流，并网PWM逆变器将高压直流电转换成恒频恒压的交流电，经由线路等效电感输送至电网。直流侧采用超级电容构成Crowbar电路实现LVRT功能。

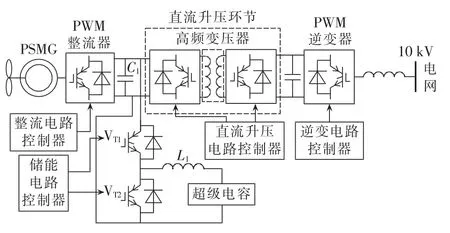
图1 基于固态变压器的永磁同步风力发电并网系统Fig.1 A grid-connected PMSG wind power system based on solid state transformer

该系统的特点是，在常规的风电系统变流器结构中加入高频变压器，形成固态变压器结构，实现整流和逆变电气隔离的同时，使并网电压升高至10 kV，大幅度减小并网电流，有利于减小风电的间歇性对电网的频繁冲击，对提高电网对风电的消纳能力十分有利。随着高电压、大容量IGBT器件的不断推出，基于固态变压器技术的高压风电并网系统将得到更多的关注与研究。

1.2 风电系统的LVRT要求

根据2009年12月22日颁布的国家电网公司企业标准Q-GDW392—2009《风电场接入电网技术规定》第8章规定，风电场LVRT要求如图2所示，图中t为电压跌落时间，U/UN为跌落深度。

图2 风电场的低电压穿越要求Fig.2 LVRT requirement of wind farm

对不同故障类型引起的并网点电压跌落，要求风电场具备以下运行能力。

a.三相短路故障引起并网点电压跌落，当各线电压位于曲线上方时，风电机组必须保持并网运行；当任一线电压位于曲线下方时，允许风电机组脱网。

b.单相接地故障引起并网点电压跌落，当各相电压位于曲线上方时，风电机组必须保持并网运行；当任意一相电压位于曲线下方时，允许风电机组脱网。

c.两相短路故障引起并网点电压跌落，当各线电压位于曲线上方时，风电机组必须保持并网运行；当任一线电压位于曲线下方时，允许风电机组脱网。

2 基于超级电容的Crowbar电路

2.1 超级电容模型

超级电容采用活性炭多孔电极和电解质组成双电层结构，将电能存储在双电层中，是一种介于物理电容器和蓄电池之间的理想短期储能元件[12-13]。它是一种复杂网络，具有复杂的物理特性，可以用分布式参数来描述其数学模型，常用的超级电容二分支模型如图3所示。

图3 超级电容的二分支电路模型Fig.3 Two-branch circuit model of super capacitor

图中，CF为可变电容，由一个恒值电容和一个电容值与超级电容静置端电压成正比的可变电容组成：CF=C0+kU；RES为等效串联电阻，表征充放电过程中的能量损耗；REP为等效并联电阻，表征超级电容器的漏电流情况，也称为漏电电阻。超级电容自放电时间通常长达数十个小时，所以在工程应用中，REP的影响可以忽略。包含CF的主分支反映超级电容充放电时能量的变化；由R2和C2构成的第二分支反映电容内部能量在中长期发生转移的现象。电路中的等效串联电感LES表现超级电容的脉冲响应特性，电感值很小，绝大多数应用中可以忽略不计[14]。

本文中的超级电容主要用于系统故障时直流母线的能量快速平衡，时间按照秒级考虑，并不涉及第二分支中的能量转移，因此采用简化等效电路，也称之为经典模型，如图4所示。

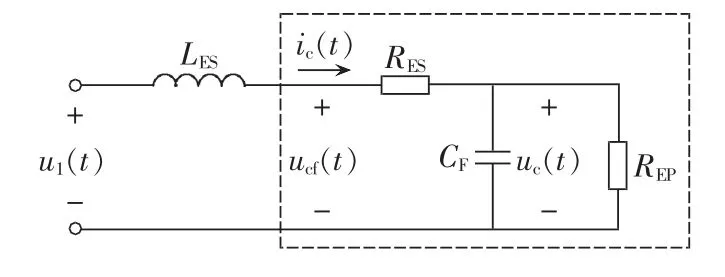
图4 超级电容的经典电路模型Fig.4 Typical circuit model of super capacitor

2.2 超级电容的充放电特性分析

由图4可得电压、电流之间的关系式：

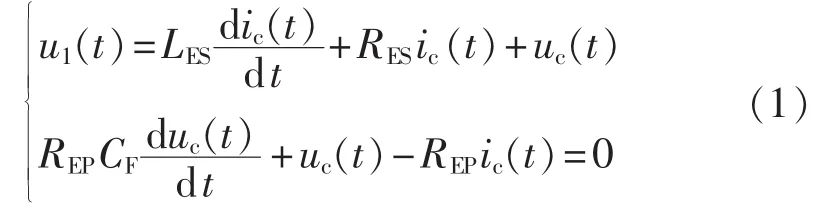
若不计等效电感LES的影响，设充电电流为icf，可得：

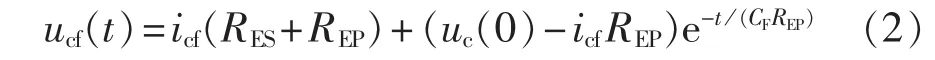
其中，uc（0）为电容的初始电压。

根据图2所示的LVRT要求，可以计算出在电压跌落期间直流母线两侧产生的能量差值，按最严重的三相短路情况计算：

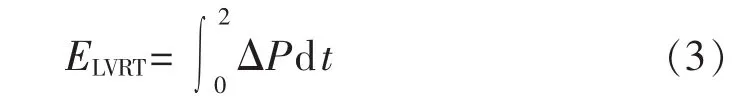
其中，积分时间指电压跌落未脱网时间。

再对应图2的数据，可得到：

其中，PN为额定并网功率；ΔP为电压跌落期间并网功率与额定并网功率的差值。

而超级电容的理想储能容量为：

其中，Uw为超级电容的工作电压。

由此可以计算出超级电容的取值范围。由于超级电容本身物理结构十分复杂，实际应用中，数量众多的电容单体串并联会引起各种损耗，并考虑电网故障在一段时间内多次发生的可能，因此，实际的电容值应在理论计算值的基础上乘以一个较大的可靠系数，以保证超级电容能可靠地吸收直流母线上多余的能量，保持直流母线电压的稳定。

根据图1风电系统的配置参数，本文Crowbar电路中的超级电容选择50 F、540 V，实际电路由200个10000 F、2.7 V的单体串联而成。根据图4所示的经典等效电路分析其充放电特性，仿真时间20 s，结果如图5所示。

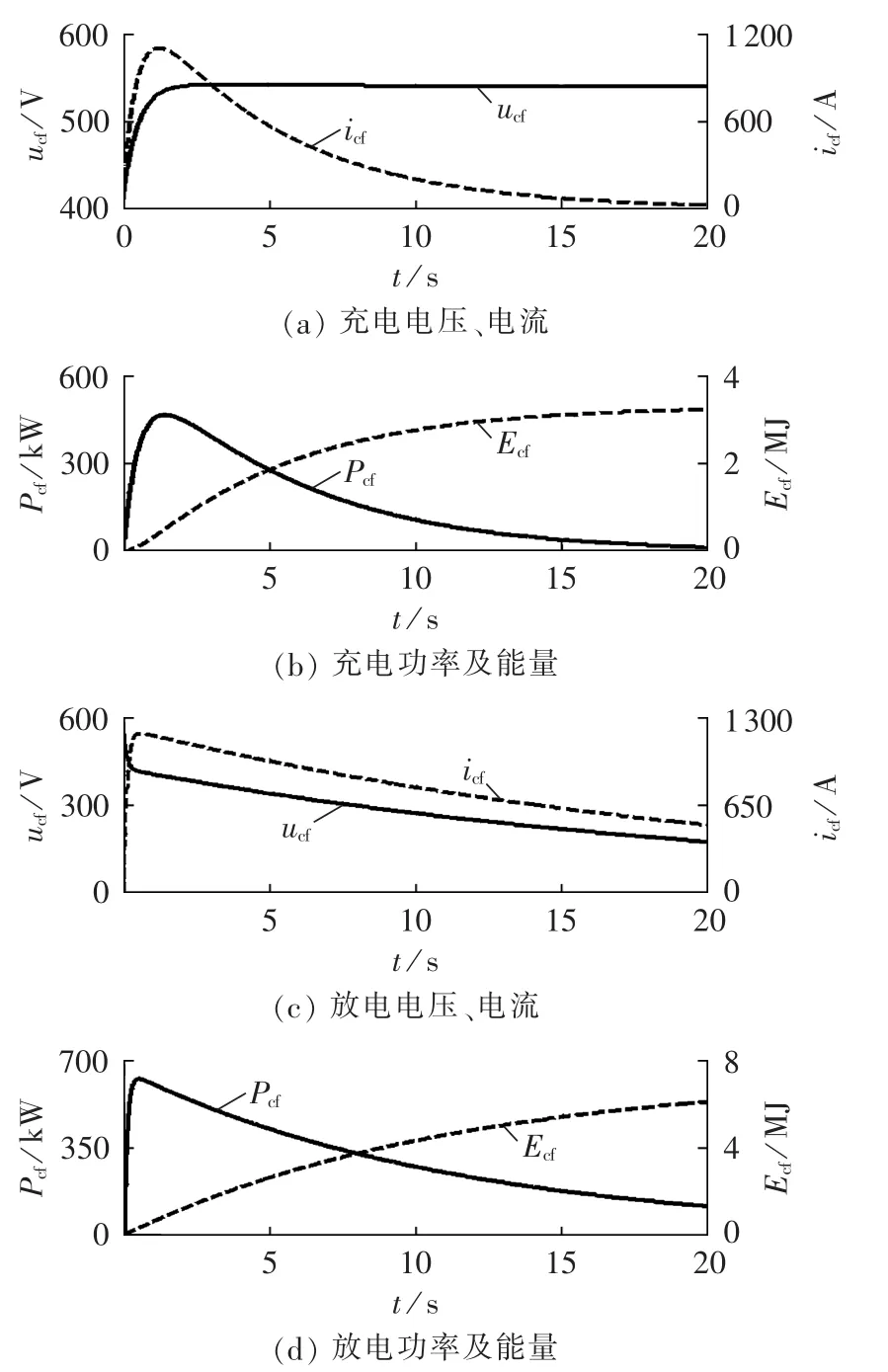
图5 超级电容器的充放电特性Fig.5 Charge/discharge characteristics of super capacitor

仿真分析表明，超级电容的充放电过程十分迅速，充电及放电电流均小于1200 A。大约在1 s时充电功率达到最大值，总计充电能量达到3.6 MJ，而在电网电压跌落期间，由于并网功率减小而导致在直流母线两侧产生的不平衡能量总和约为1.2 MJ，在超级电容的充电能量范围以内，因此该超级电容能够有效吸收直流母线上的多余能量，使直流电压维持在稳定值，从而不影响整个系统的正常运行。

2.3 Crowbar电路的控制

采用超级电容的Crowbar电路如图6所示。

双向半桥Buck-Boost电路的工作模式由直流母线两端功率的不平衡状况决定。设发电机发出的功率为Ps，系统输出的并网功率为Pg。稳态时，Ps与Pg近似相等，电路不投入工作；当Ps＞Pg时，VT1触发，电路工作于Buck模式，超级电容吸收能量；当Ps＜Pg时，VT2触发，电路工作于Boost模式，超级电容释放能量。在实际应用中，可以用母线电压的变化作为功率变化的判据，控制框图如图7所示。

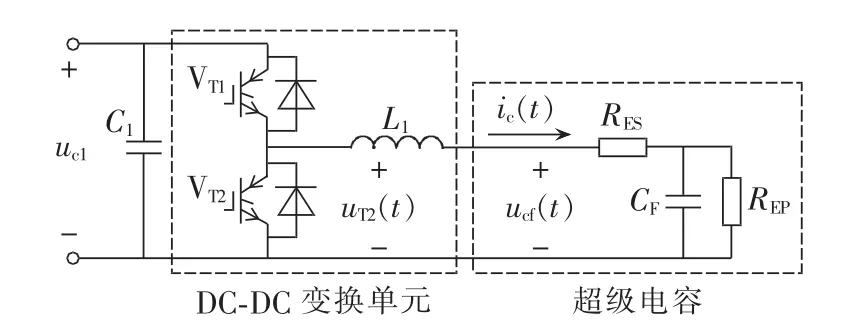
图6 采用超级电容的Crowbar电路Fig.6 Crowbar circuit with super capacitor

图7 Crowbar电路的控制框图Fig.7 Block diagram of Crowbar circuit control

3 并网逆变器的控制

3.1 电压定向矢量控制

并网逆变器的控制目标为：保持直流母线电压恒定；实现有功功率和无功功率的解耦控制。其模型表示为：

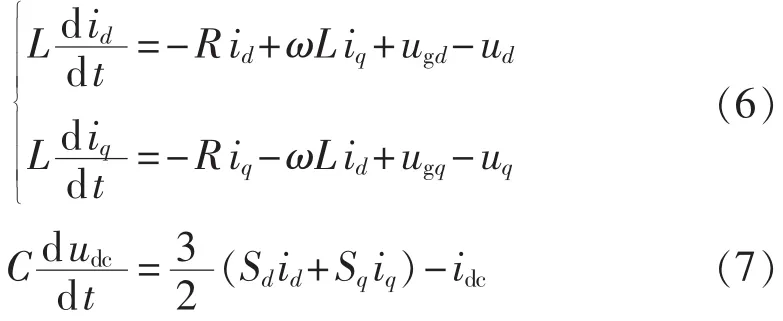
其中，L、C、R分别为并网逆变器的滤波器等效电感、电容和电阻，udc和idc分别为低压直流侧电压和电流，ud、uq分别为并网电压的 d、q 轴分量，ugd、ugq为电网电压 ug的 d、q 轴分量；id、iq为并网电流的 d、q 轴分量；ω为电网角频率；Sd、Sq为开关函数。

风电机组馈入电网的有功和无功功率为：

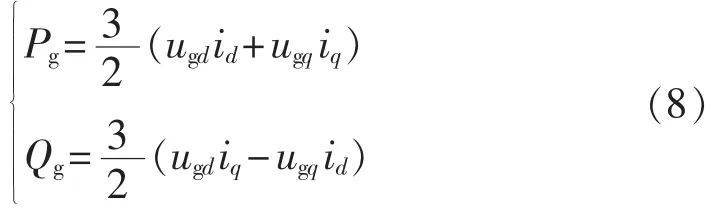
令d轴定向于电网电压矢量，将直流侧电压误差送入PI控制器，输出id*为参考值，控制输出有功功率，无功功率设定为0，使系统运行在单位功率因数状态。得到逆变器的双环解耦控制框图见图8。

图8 电网侧逆变器的解耦控制图Fig.8 Decoupling control of grid-side inverter

3.2 正负序电压定向矢量控制

当风电并网点的电压发生不对称跌落时，直流母线电压将产生2次纹波，并网电流产生3次谐波。而直驱式永磁风电系统通常采用三相无中性线并网，零序分量不能以中性线为通路。因此三相不平衡电压和电流可用对称分量法分解成正序和负序分量，而不存在零序分量。分解后的正序和负序分量分别对称，可分别控制。

风电系统的功率传输方程为：

其中，PC为电容的充放电功率；Ps为发电机的输出功率；Pg为并网功率，P0、P1和P2分别为并网有功功率的稳态分量、2次谐波余弦和正弦量的峰值。

不对称故障下，风电系统传输的功率中存在2次谐波分量，P1、P2不为0，从而引起直流母线电压2倍工频波动，继而影响发电机侧的正常运行。需要采用不同于对称故障的控制方法，令功率方程式（9）中的 P1=0、P2=0。

由文献[2，6，15]，将不对称电压和电流作正负序分解，得到正序与负序同步旋转坐标系下的电压方程：

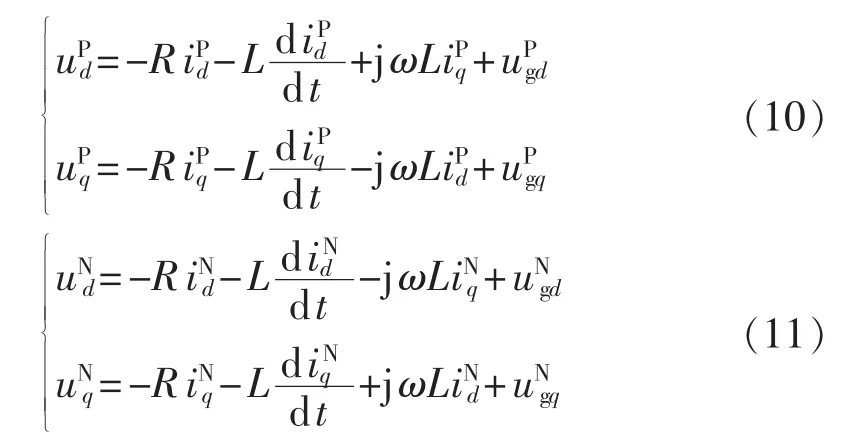
其中，上标“P”、“N”分别表示正序、负序。

将电网电压定向控制策略引入正负序网络，在正序网络中令dP轴定向于正序电压方向，在负序网络中令dN轴定向于负序电压方向[6]，得到逆变器的电流给定与功率输出的关系：

其中，D=（UPm）2-（UNm）2，UPm、UNm为正序、负序电压幅值。

由此得到正负序电压定向矢量控制框图如图9所示。

4 仿真分析

4.1 系统参数和仿真工况

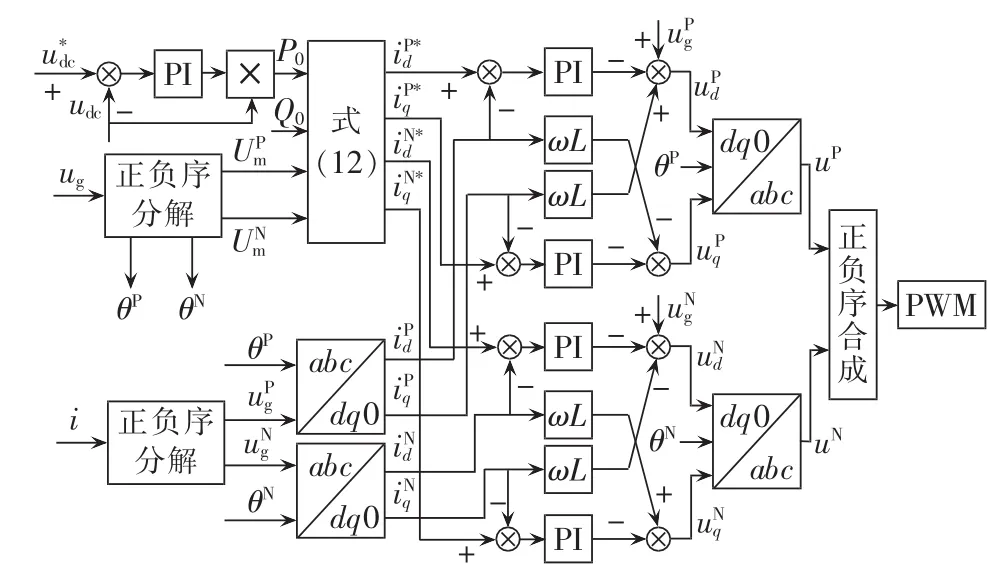
图9 正负序电压定向矢量控制原理图Fig.9 Schematic diagram of positive/negative voltage oriented vector control

在MATLAB/Simulink环境下建立图1所示风电系统的仿真模型，系统参数如下：对于风力机，额定风速 12 m/s，桨叶半径 31 m，额定转速 20 r/min，最佳叶尖速比5.6，风能利用系数0.33；永磁发电机，额定功率1 MW，发电机端线电压690 V，永磁体磁链6.27 Wb，极对数 48，定子 d、q 轴电感 Ld=Lq=2 mH，转动惯量2.5×104kg/m2；对于系统，直流母线电压uc1=1200V、udc=1.8×104V，并网线电压 ug=10 kV；对于超级电容器，等效电容CF=50 F，等效串联电阻RES=0.1 Ω，等效并联电阻 REP=2×104Ω。

三相电压对称跌落时，对比仿真Crowbar电路接入前后风电系统的直流电压、并网电流和功率的变化情况，验证Crowbar电路控制效果和能量消纳性能。

电压不对称跌落时，分别对单相跌落和两相跌落2种情况进行仿真。并对比了三相电压平衡控制策略和正负序电压定向控制策略下LVRT的实际效果。

4.2 三相电压对称跌落

4.2.1 未接入Crowbar电路时的工况

风电系统直流侧未加储能电路时，仿真结果如图10所示，图中ug、uc1为标幺值，系统对称，交流电压只取a相说明。

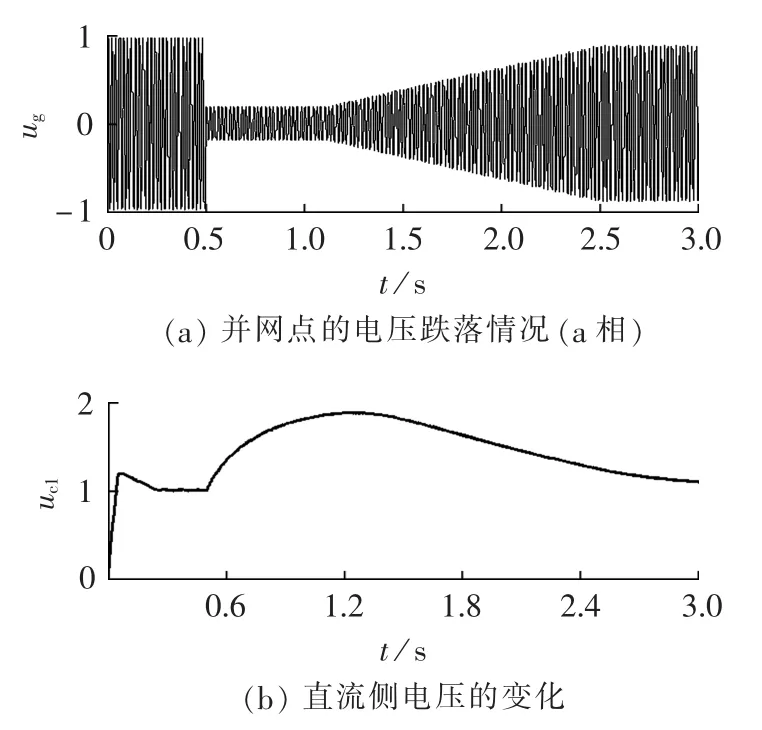
图10 未加Crowbar电路时的相关波形Fig.10 Waveforms without Crowbar circuit

由仿真结果可知，并网点电压跌落期间，直流侧电压上升幅度较大，近于2倍额定值。

4.2.2 接入Crowbar电路后的工况

为了提高风电系统的LVRT能力，在直流侧增加图6所示由超级电容组成的Crowbar电路。在同样的运行条件下仿真结果如图11所示，图中uc1、ug、ig、Pg为标幺值。

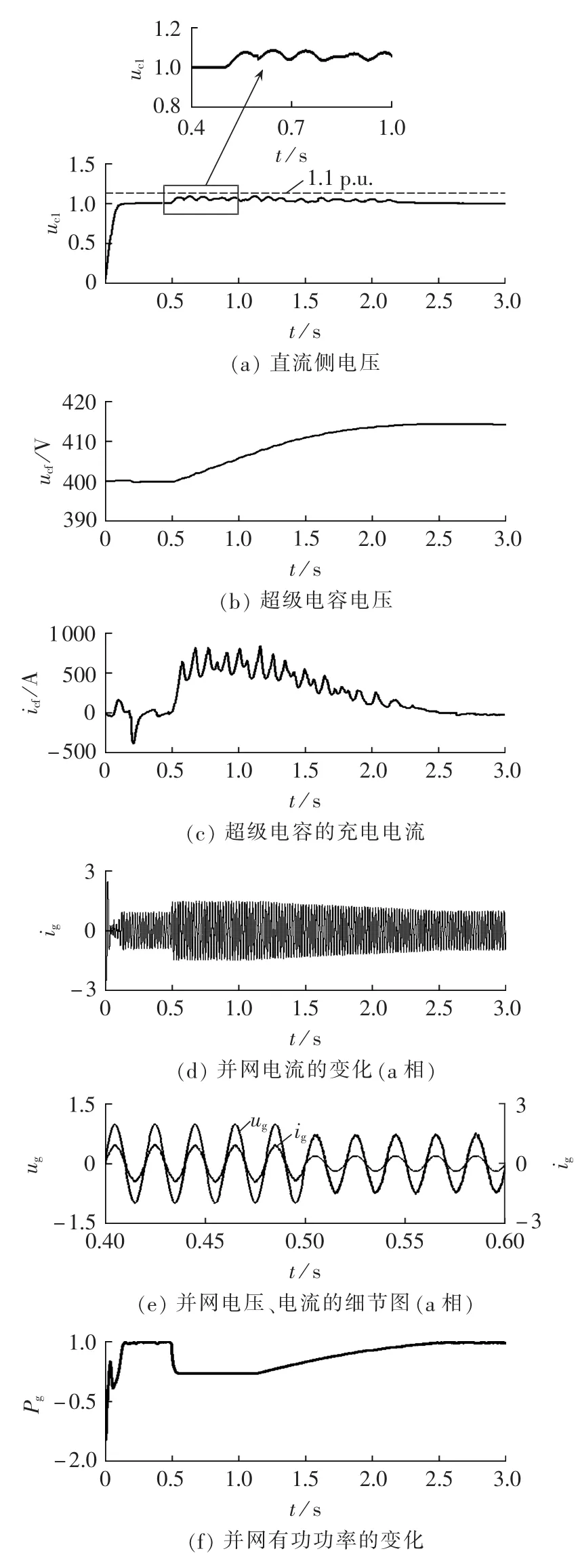
图11 增加Crowbar电路时的相关波形Fig.11 Waveforms with Crowbar circuit

仿真结果表明，电网电压跌落期间，并网电流不超过1.5 p.u.，直流电压维持在1.1 p.u.以内，超级电容从初始电压400 V开始充电，充电电流峰值约为800 A，0.5 s电网电压跌落至20%额定值，并网功率减小。在后续的仿真中，均采用图6所示Crowbar电路，重点比较2种控制策略的效果。

4.3 单相电压跌落

仿真结果表明，并网点发生单相电压跌落时，仅靠逆变器出口的支撑电容就可以平抑直流母线的功率波动，超级电容构成的Crowbar电路不需要投入工作，风电系统即可继续并网运行。

采用传统的逆变器控制方式时，不能对负序电流实现无差调节，直流母线电压出现明显的2次纹波，并网电流有较大的3次谐波分量。采用了正负序电压定向的控制方法后，直流电压的2次纹波得到了很好的消除，并网电流的谐波也得到了明显的抑制。具体仿真结果如图12所示，图中uc1为标幺值，幅值为占基波百分比。

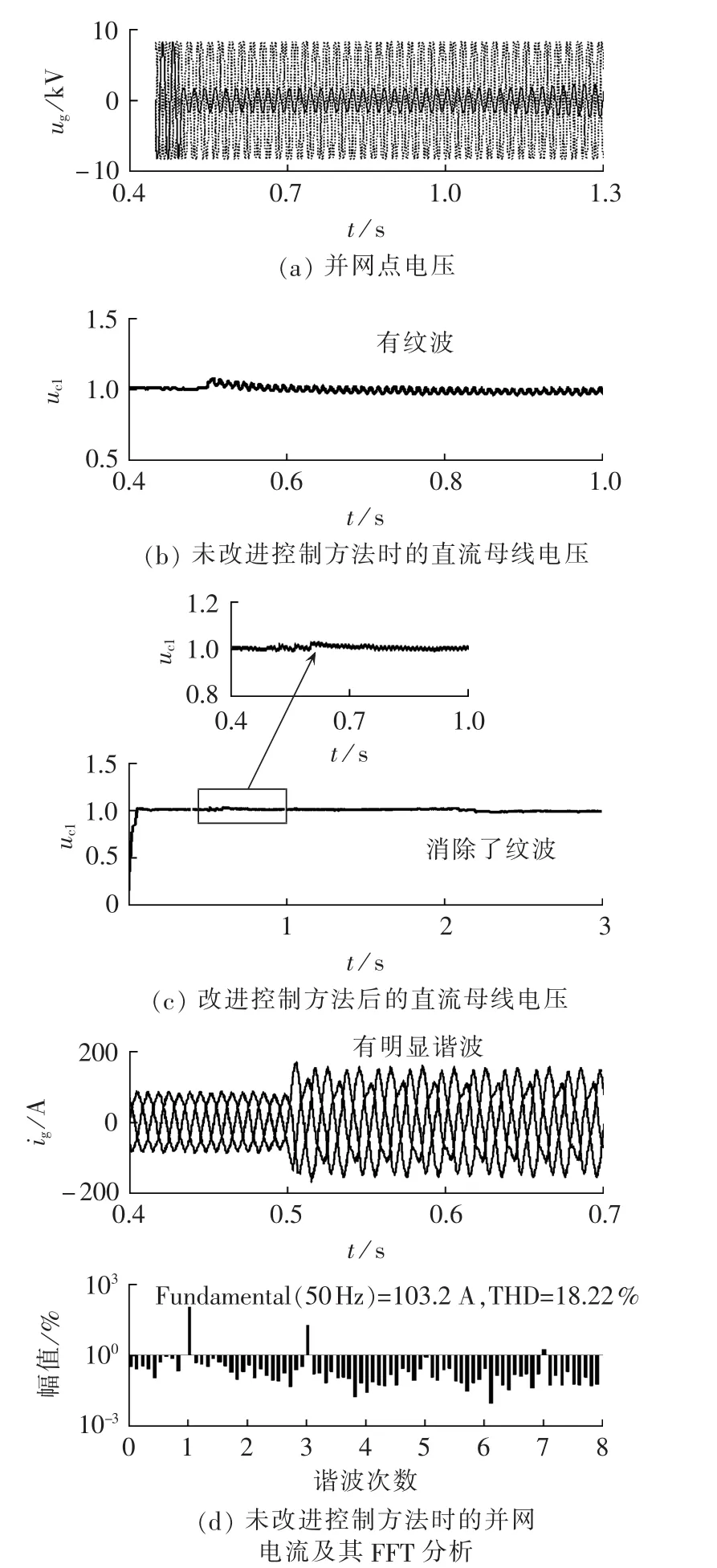
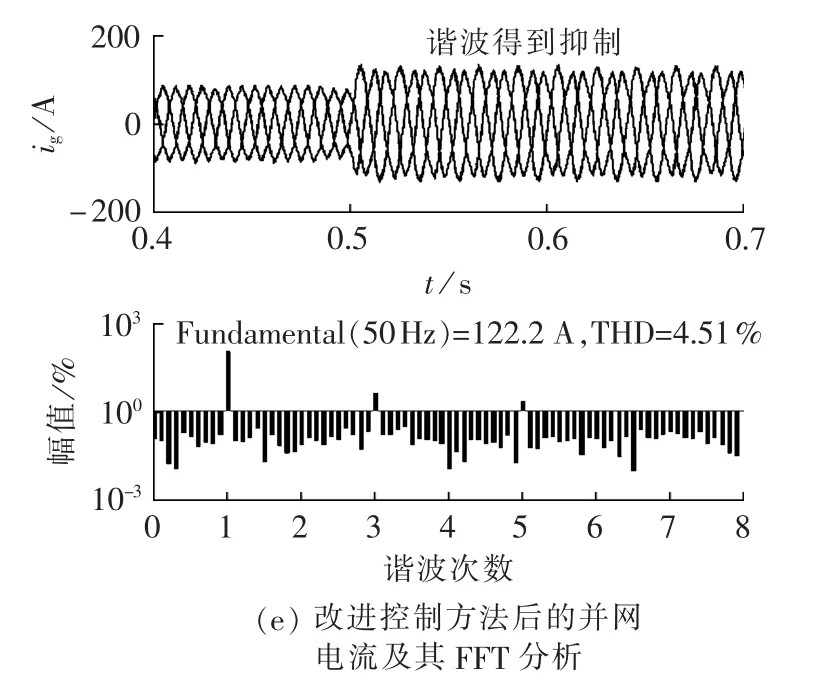
图12 单相电压跌落时的相关波形Fig.12 Waveforms during single-phase voltage drop

4.4 两相电压跌落

发生两相电压跌落时，超级电容构成的Crowbar电路投入工作，使直流侧电压维持在1.1 p.u.以内，实现了LVRT功能。超级电容的充电电流峰值约为300 A，比三相电压跌落时的充电电流小很多。与单相电压跌落相似，采用传统的电网电压定向控制时，直流母线电压同样出现明显的2次纹波，并网电流中有3次谐波分量，采用了正负序电压定向控制方法后，2项指标均得到明显改善。定量分析表明，相比于单相电压跌落，两相电压跌落所引起的母线电压纹波和并网电流谐波均有所减弱，这也符合对称分量法的推导结果。图13给出了对比仿真波形，图中uc1为标幺值，幅值为占基波百分比。

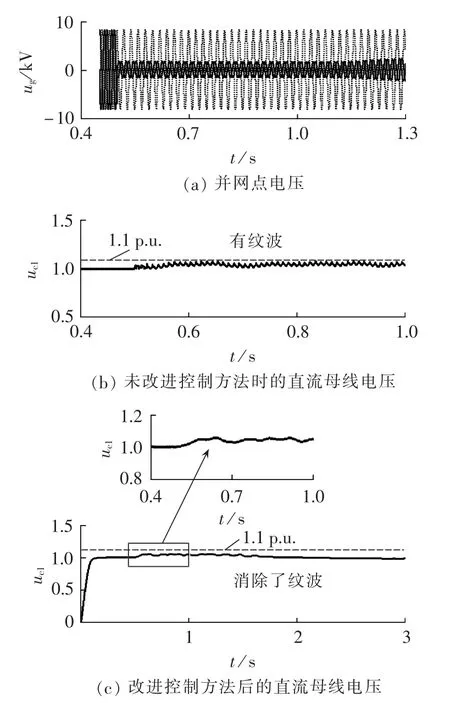
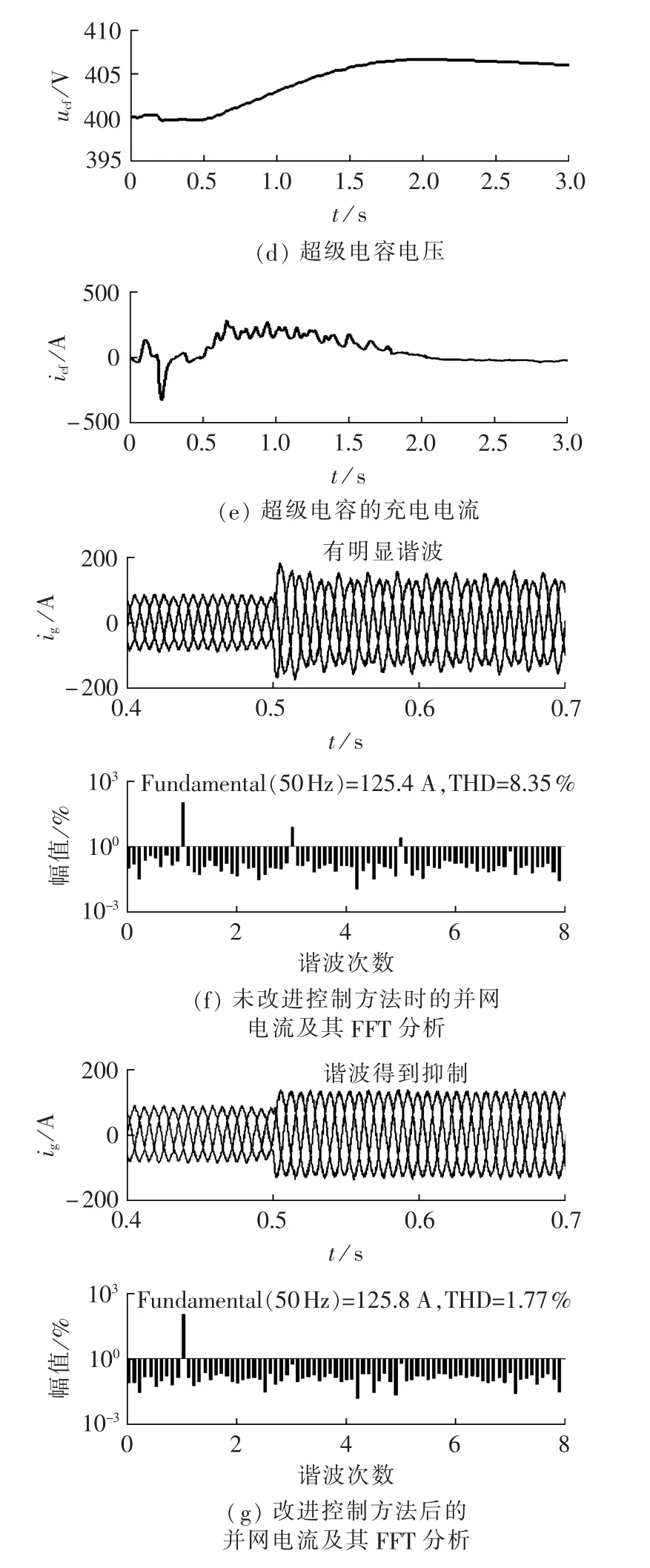
图13 两相电压跌落时的相关波形Fig.13 Waveforms during two-phase voltage drops

5 结语

本文将超级电容的经典模型应用于风电系统LVRT电路的分析，并给出基于电容充放电特性的超级电容容量计算方法。建立了基于固态变压器结构的永磁同步风电系统仿真模型，逆变器并网控制采用正负序电压分别定向控制策略。仿真研究表明，所提出的LVRT电路的参数选择合理，控制方法有效，所设计的风电系统具备可靠的LVRT能力。

本文所提出的基于超级电容的LVRT功能分析与计算方法对大容量风电并网系统的理论研究与工程设计都具有参考意义。