考虑风储一体的多场景两阶段调度决策模型

高红均，刘俊勇，魏震波，刘友波，王 玮，李 霞

（1.四川大学 电气信息学院，四川 成都 610065；2.甘肃省电力公司，甘肃 兰州 730050）

0 引言

大规模风电并网后，风电功率的波动性和不确定性给电力系统的安全稳定运行带来了新的挑战，同时给电网调度方面包括常规机组启停机、爬坡速率、备用容量等产生了较大影响。

针对上述调度问题，国内外学者做了大量研究。文献[1]从建模和求解方法两方面综述了含风电场的电力系统经济调度问题，同时也分析了风电不确定性求解方法，但仅停留在理论层面上，未进行实际分析。文献[2-3]分别考虑了风电波动风险成本和可靠性约束，建立了随机动态经济调度模型，并论证了各自方法的有效性，但未深入挖掘风电的不确定性。文献[4]分别建立了基于点预测、区间预测、场景预测的机组组合综合模型，分析了不同预测信息下的优化结果，得出合理弃风有利于更优的经济运行。文献[5]建立了计及风电预测误差带的调度计划渐进优化模型，用分位点回归技术得到预测区间，从而表征风电的不确定性，并根据最新预测信息对日前调度计划进行调整。另外，国内一些学者在滚动调度方面也有一定的研究[6-7]。

在已有研究的基础上，本文将综合考虑风电的不确定性和弃风、切负荷成本，建立基于场景集的日前机组组合和日内滚动修正两阶段调度决策模型。所做主要工作与特点在于：日前机组组合模型是在具有一定保守度的不确定性场景集上建立的，而日内滚动经济调度则在日前的调度计划基础上，并根据最新的预测信息作出相应调整；同时引入弃风量和切负荷量作为松弛变量，用以提高模型的收敛性；在模型中引入储能系统对风电功率波动进行抑制[8-11]。最后将通过10机算例对所提模型进行验算。

1 基于场景集的日前机组组合模型

1.1 场景集的生成

场景集的思想在含风电的电力系统调度中得到了广泛应用[12-13]。和传统场景的选择不同，本文场景的生成主要考虑风电出力的不确定性波动误差。假设实际第t时段的不确定性风电功率出力Pwt服从基于预测功率Pft的正态分布。场景集的波动大小取决于误差分位点α的取值。α的物理意义表示系统能够接纳的风电至少为α，或者满足负荷的概率至少为α。根据分位点可以得到场景集允许的风电最大误差上、下出力 Pht、Ptl， 其中 F（Plt）=1-α，F（Pht）=α。 设 ft+=1表示第t时段的场景出力达到正的最大波动误差Pht，ft-=1表示第t时段的场景出力达到负的最大波动误差Plt，ft-=0和ft+=0表示第t时段波动较小，出力为预测值Pft。另外，为了使日前机组组合解在较大的风电出力误差下具有较强的鲁棒性，定义一个场景保守度指标NB，NB表示允许风电出力较大波动的时段数，其中0＜NB＜T（T为调度周期总时段数），NB越大，表示生成的场景集越保守[14]。因此可以得到相应的不确定性场景集Ωs。

不同场景集Ωs就构成了整个调度场景约束集ΩS。本文的场景集应用于日前机组组合中，来决定次日的常规发电机机组状态。

1.2 基于场景集的模型基本原理

由于实际风电功率存在一定误差，就决定了含风电的日前调度计划是一个包含不确定性的优化问题。本文的机组组合模型用场景集刻画风电出力的不确定性，在目标函数中对各场景赋予相应的权重，从而求得相应优化解，同时也满足相应的场景约束。

一般模型如下：

其中，s为场景数；S为风电场景数；ωs为场景s下的权重；ξs为场景s下的不确定量；Us为场景s下的不确定集；m为约束条件总数。

1.3 含风电的机组组合模型

1.3.1 目标函数

含风电的日前机组组合模型是对次日发电机组出力的计划，目标函数只包含常规机组运行成本。

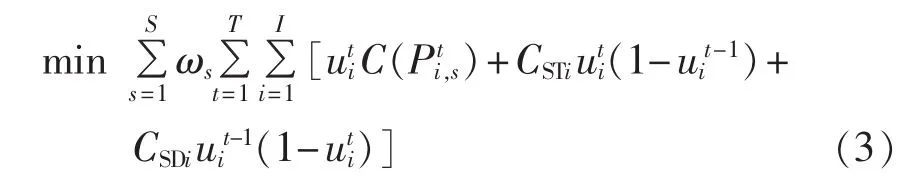
其中，T为调度周期的总时段数；t为时段编号；I为常规机组总数；i为常规机组编号；Pti，s为场景s下常规机组 i在第 t时段的有功出力；C（Pti，s）为常规机组发电成本；CSTi、CSDi分别为常规发电机组i的开机、停机费用；uti为常规机组状态标志。

1.3.2 约束条件

a.功率平衡：

b.发电机组功率限制：

c.备用需求：

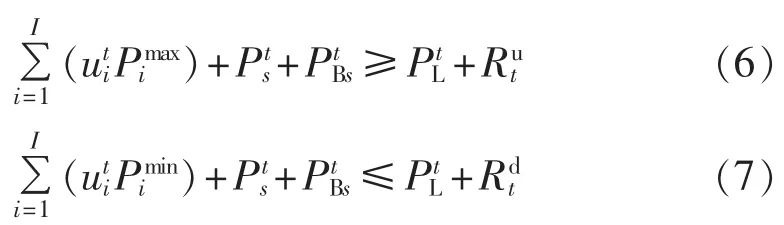
d.爬坡率限制：

其中，Pts为场景s下第t时段的风电出力；PtBs为场景s下储能装置第t时段的出力；PLt为系统第t时段的负荷功率；Pimax、Pimin分别为常规电机组i出力的上、下限；Rtu、Rtd分别为系统第t时段的上、下备用需求；RUi、RDi、SUi、SDi分别为常规电机组 i的爬坡速率、滑坡速率、开机爬坡速率和停机爬坡速率。

e.储能装置的相关约束有以下3个方面。

充放电状态限制：

功率极限：

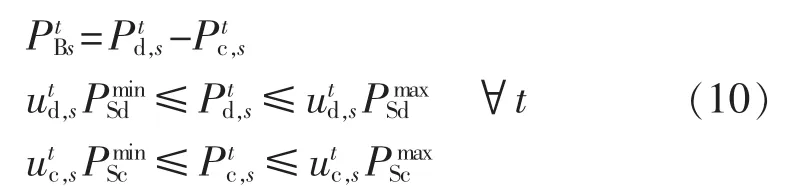
容量限制：

其中，Pdt，s为蓄电池储能装置在第t时段的放电功率；为蓄电池储能装置在第t时段的充电功率；为储能装置在第t时段的电量；αc、αd分别为充、放电系数；PSmdax、PSmdin，EBmax、EBmin分别为储能装置的功率与容量上、下限；utc，s为蓄电池装置场景s下的充电状态，utc，s=1 表示装置处于充电状态，utc，s=0 表示装置处于空闲或者放电状态；udt，s为蓄电池装置放电状态，udt，s=1表示装置处于放电状态，utd，s=0表示装置处于空闲或者充电状态。蓄电池储能装置在同一时间内充放电过程不能同时进行。

f.机组最小开停机时间约束：采用文献[13]的最小开停机时间约束。

由此构成了含风电的机组组合数学模型。

2 日内滚动经济调度修正模型

日内滚动经济调度修正模型是根据最新的预测信息和负荷需求等，对之前制定的调度计划进行的滚动调整。滚动修正阶段，由于更接近真实运行情况，并且合理弃风或切负荷能提高大规模风电的消纳能力[2]，因此引入了弃风量和切负荷量，允许一定弃风和切负荷，既考虑了系统运行的经济性，同时从数学角度上，把弃风量作为一个松弛变量，保证模型存在可行解，从而具有意义[4]。

由于滚动修正模型在数学上是一个NP难题，模型复杂，耗时较多，为了简化运算量，只有当预测负荷需求和计划出力之间出现较大差值，即超过一定的阈值，才对当前时段以后的计划出力作出修正[7]，且不改变日前机组组合模型得到的机组状态。

2.1 目标函数

由于之前的机组组合模型在日前调度计划上考虑了一定的风电出力不确定性，因此该阶段模型主要偏向于系统的经济性。由文献[6]可知滚动调度的启动周期为30～60 min，本文的调度周期为1 h，因此提前从当前时段的后一时段开始修正从实际意义上是可行的。目标函数为：

其中，t0为当前时段；F1、F2、F3分别为发电成本、弃风成本、切负荷成本；Cw为单位弃风成本，Ptw，t0为 t0时段对第t时段的风电预测功率；Ptw为第t时段的风电调度功率；CL为单位切负荷成本；时段对第t时段的负荷需求预测；PLt为第t时段满足的负荷需求。t0取0时，表示日前调度计划。

2.2 约束条件

对于日前机组组合模型，由于调度修正模型中加入了弃风量和切负荷量作为松弛变量，需要对约束条件进行部分改动。

a.功率平衡：

b.风电调度功率（弃风量）约束：

c.切负荷约束：

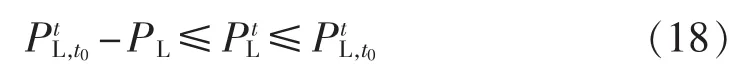
其中，PL为允许的最大切负荷量。除了上述功率约束以外，该阶段修正模型还包括备用约束、爬坡约束、储能装置相关约束。另外，一般不改变由日前机组组合模型决定的机组组合状态。

3 算例分析

本算例采用10机系统进行验证，该系统包含10台常规发电机组、1个风电场和1个蓄电池储能系统。常规机组的爬坡能力和蓄电池的相关参数参见文献[13]，10 台常规机组参数参见文献[15]，并模拟实际运行情况，NB=8。

3.1 模型求解及调度流程

该两阶段调度优化模型是一个混合整数规划模型，采用cplex商业优化软件进行求解，图1为整个优化模型两阶段调度流程图。

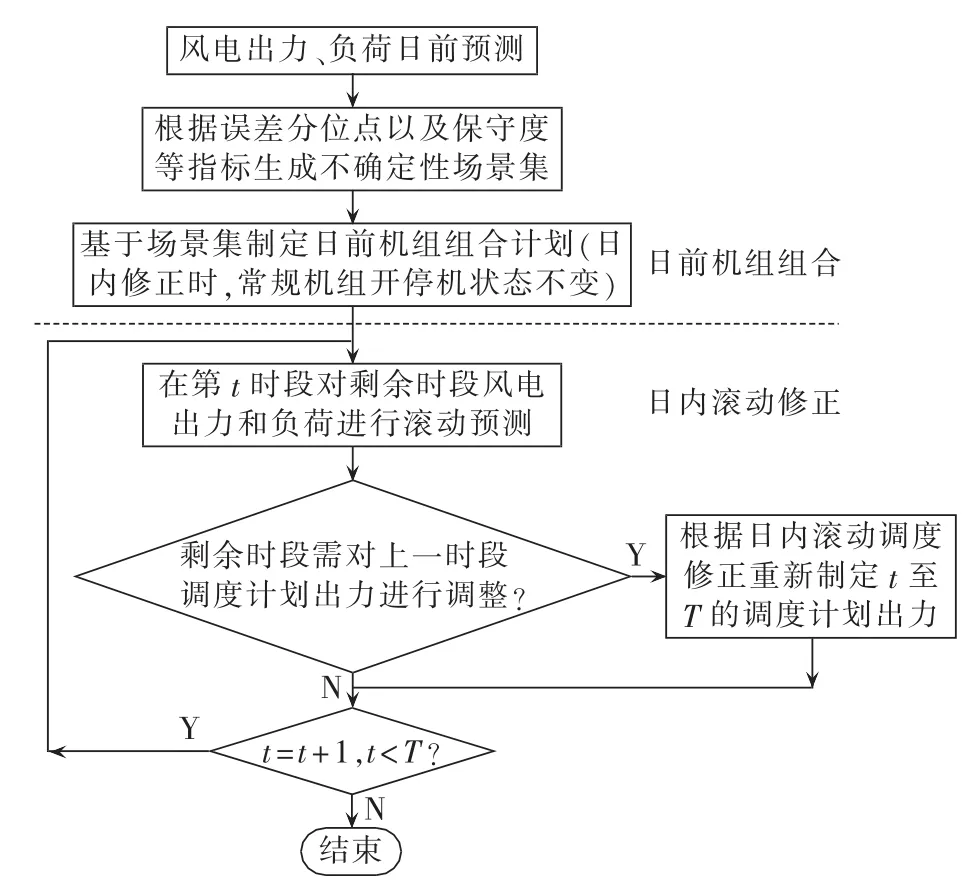
图1 两阶段调度流程图Fig.1 Flowchart of two-stage dispatch

3.2 模型结果

表1为基于场景集的10机日前机组组合状态结果。

表1 各发电机组状态Tab.1 Generator states

在表1的机组组合状态下，选择一个约束条件检验日前机组组合模型的适应度。在此选择备用约束即不同场景下的发电充裕度，如图2所示。

图2 各场景下的发电充裕度Fig.2 Generation adequacy of different scenarios

由图2可发现，只有极少时段处于备用需求临界点上，其他时段均有一定量的发电充裕度，表明该日前机组组合状态在不同的场景下均能较好地满足系统要求，同时也说明了该模型有较好的适应度。

根据表1确定的日前机组组合状态，并根据滚动预测信息进行修正得到各时段机组调度计划出力，如表2所示。

设弃风成本为 2 000$/（MW·h），切负荷成本为200$/（MW·h）。由于日前机组组合状态是基于一定抗风险的不确定性场景集建立的，弃风成本高于切负荷成本，因此模型结果未出现切风量，切负荷量为35 MW·h，运行成本为$417160。

表2 各发电机组出力Tab.2 Generator power outputs

3.3 模型分析

3.3.1 有无场景集的对比分析

将算例中的场景集去掉，采用传统的不计及风电不确定性的日前机组组合模型求出日前机组组合状态。根据日前机组组合状态固定来求解日内滚动修正解，无法收敛；不固定常规机组状态，根据滚动预测风电和负荷数据进行调节机组状态出力和有功出力，所得运行成本为$438990，包括$421 390的常规机组发电成本、$13600的切风成本和$4000的切负荷成本。与本文模型算例对比可得：

a.由于机组启停未固定，日内模型的修正增加了启停次数，从而增加了常规机组发电费用；

b.常规模型不计及风电的不确定性，而风电预测出现一定误差，实际风电出力存在波动性，这导致了更多的弃风成本和切负荷成本。

因此，基于场景集的日前机组组合模型能更好地抑制风电不确定性和波动性带来的影响。

3.3.2 有无松弛变量（弃风量和切负荷量）的对比分析

将算例修正模型目标函数中的弃风和切负荷成本以及约束条件中弃风量和切负荷量去掉，得到无松弛变量的修正模型，但模型不收敛。由此可得：松弛变量的引入对模型的收敛性有着重要的意义，有效地解决了经济调度修正模型不收敛的问题。因为基于场景集的日前机组组合具有较强的抗风险性、抗不确定性，但是实际的机组爬坡率等原因可能导致无法通过仅修正常规机组出力来跟随负荷的随机性，因此必须通过松弛变量（弃风量和切负荷量）来进行调整，进而提高模型的收敛性。另外，设置弃风成本高于切负荷成本，使得优先利用切负荷来抑制风电波动性，有利于系统接纳风电的能力，提高风电利用率。

3.3.3 不同保守度下的对比分析

将算例中的NB增至12，其他参数不变，即增大了场景集的保守度，使得日前机组组合模型更保守，计及了更大的风电不确定性，得到各发电机计划出力见表3。运行成本为$429750，其中包含55 MW·h的切负荷量对应的切负荷成本$11 000和常规机组$418750的发电成本。

表3 NB=12下的各发电机组出力Tab.3 Generator power outputs at NB=12

通过对比分析，可以得出：由于NB更大，从而得到更加保守的不确定性场景集，日前机组组合模型计及了更多的不确定性以及更大的波动性，但由于约束性和抗波动性更强，导致了更高的发电成本代价，进而产生更多的运行成本，不利于系统的经济运行。另外，NB越大，可能导致切负荷量越大，这是由于NB越大使得模型更具抗风险性、抗不确定性，进而日前决策更加保守，但是由于实际风电出力和机组爬坡率等原因，需要更大的松弛量来调节。相反，NB越小，所获得的场景集能够表征风电出力不确定性的能力就越小，日前机组组合模型就只能得到计及更小波动性的优化解。因此，NB过大虽然在抑制不确定性上更优，但它是以更大的成本作为代价，选择合适的NB值，能兼顾系统经济性和抑制风电波动性。

3.3.4 储能装置容量分析

改变储能装置容量，其他参数不变，NB=8，得到不同储能装置容量下的切负荷量，如表4所示。

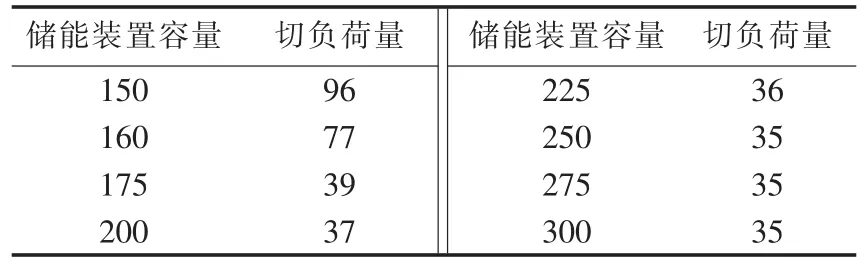
表4 不同储能装置容量下的切负荷量Tab.4 Shedding load for different storage capacities MW·h

另外，常规机组发电成本和切负荷成本的对比情况见表5。

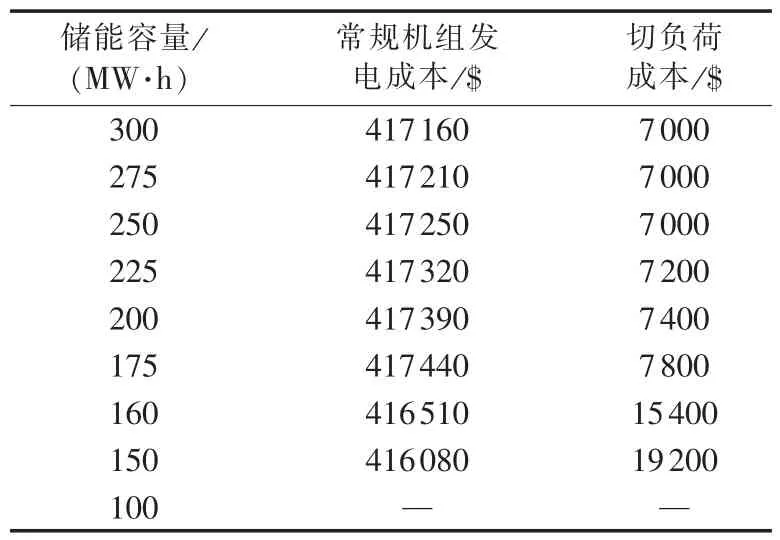
表5 不同储能装置容量下的运行情况对比Tab.5 Comparison of operating condition among different storage capacities

由于切负荷成本低于弃风成本，在该模型下每种运行情况都无弃风量。当储能装置容量减少到100 MW·h时，滚动调度修正模型从第5时段开始没有收敛解。由表4和表5可以得出：

a.总体上，储能装置容量的减少会导致切负荷量的增加、总运行成本（包含常规机组发电成本和切负荷成本）的增加；

b.当储能装置容量大于一定阈值（该算例中为175 MW·h）时，增大装置容量对系统的常规机组发电成本和切负荷量影响都不大，这是由于基于场景集的日前机组组合模型具有一定的抗不确定性和波动性，可以通过调节机组出力进行抑制，但容量下降到一定程度会导致模型没有收敛解，因此系统必须配置一定容量的储能装置来平抑风电的波动。

4 结论

本文建立了两阶段调度优化模型，包含基于一定不确定性场景集的日前机组组合模型和根据最新预测信息作出相应调整的日内滚动修正模型。

通过算例分析表明：

a.基于场景集的日前机组组合有效地抑制了风电的不确定性和波动性，并减少了启停成本、弃风成本和切负荷成本，增强了滚动调度模型的鲁棒性；

b.松弛变量的引入，有效地解决了日前机组组合的不确定性场景集导致日内滚动修正模型不收敛的问题；

c.更大的保守度指标NB是以更大的成本作为代价，选择合适的NB，兼顾系统经济性和抑制风电波动性；

d.系统必须配置一定容量的储能装置，但容量增大到一定程度后，继续增加容量对系统的常规机组发电成本和切负荷量影响都不大，这为系统储能装置容量的配置提供了一定参考。

本文未考虑储能系统成本给调度优化带来的影响，计及储能成本的调度优化模型将是下一步研究工作的重点。