同相牵引供电系统控制策略研究及仿真分析

黄小红，李群湛，杨乃琪，舒泽亮

（西南交通大学 电气工程学院，四川 成都 610031）

0 引言

电气化铁道的谐波、无功、负序及电分相等问题一直受到各界关注。由于牵引负荷单相、非线性，且具有随机波动性的特点，造成电力系统三相不平衡，负序、谐波和无功严重影响公用电网的电能质量[1-2]。文献[3-5]讨论了采用高压大容量的静止无功补偿器 SVC（Static Var Compensator）、有源滤波器 APF（Active Power Filter）对电气化铁路负序、谐波和无功进行综合补偿的方案。日本在新干线投运的铁路功率调节器 RPC（Railway static Power Conditioner），实现了无功功率、负序和谐波电流的综合补偿[6]。然而，受牵引供电模式和系统结构的限制，以上工作均无法消除电分相环节。电分相环节给电力机车快速平稳运行带来安全隐患，制约了高速、重载铁路的发展[2]。

为进一步提高电气化铁路的供电性能，更好地适应高速铁路的发展要求，文献[7-8]提出了同相供电系统理论，并针对无源补偿装置实现同相供电做了大量的研究。近年来，基于平衡变压器和综合潮流控制器 IPFC（Integrated Power Flow Controller）的同相供电系统成为研究的热点[9-16]，它可有效消除电分相环节，并可实现负序、谐波和无功的动态补偿，因此正逐步得到人们的青睐。

关于IPFC的控制方法，通常采用的是比例积分（PI）和滞环比较控制策略，其负序和谐波的补偿效果有限，直流侧电压波动较大，值得进一步改进。本文首先介绍了Scott平衡变压器与IPFC构成的同相供电系统，分析了负序和谐波电流补偿原理，并基于电流内环的滞环比较控制理论，提出了直流侧电压PI均值前馈控制策略，使负序得到改善。为进一步降低谐波分量，稳定直流侧电压，提出直流侧电流均值前馈控制方法，使系统的动态特性进一步提升、稳态误差进一步减小。控制方法在牵引和再生制动工况下均适用。最后通过仿真分析验证了本文所提控制方法的有效性与正确性。

1 同相供电系统结构及补偿原理

如图 1所示，IPFC接于Scott平衡变压器副边α、β 2个端口，将原有的两相牵引供电方式转变为仅由α端口供电的单相方式，实现不同变电所供电的区段接触网电压同相位且无电分相环节的同相供电系统。

图1 同相牵引供电系统Fig.1 Co-phase traction power supply system

平衡变压器两侧的电流变换关系为[1]：

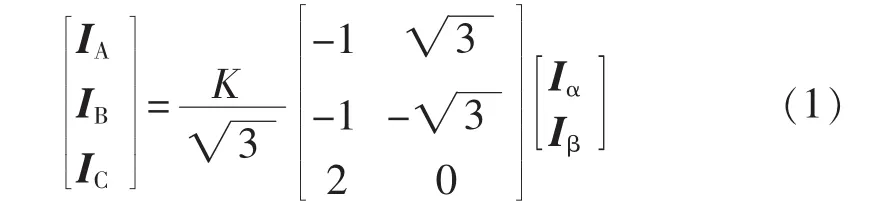
牵引侧各端口电流在三相系统中造成的总负序电流 I（-）为[17]：

其中，Ks为牵引变压器副边端口电压与一次侧线电压之比；Is为牵引变压器副边端口电流有效值；ψs为牵引变压器副边端口接线角；φs为牵引变压器副边端口的功率因数角。对于Scott平衡变压器，S=2，K1=K2=K，ψ1=90°，ψ2=0°，故可得：

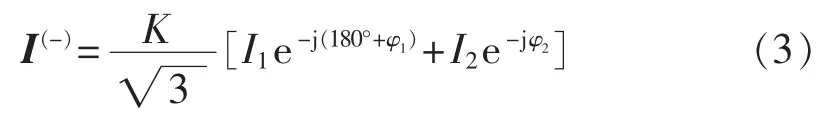
式（3）表明，当 I1=I2、φ1=φ2时，负序为 0，原边电流IA、IB、IC对称，可完全消除对电力系统的影响。

IPFC的构成如图2所示，其核心为2个背靠背连接的电压源变流器，中间通过直流电容耦合并提供直流电压。T1、T2是变比为k的降压变压器，起降低电压等级和隔离的作用。为滤除直流环节的偶次谐波，常在C所在支路并入LC滤波器组。

图2 IPFC结构Fig.2 Structure of IPFC

设IPFC的2个端口电压为：

负载电流为：

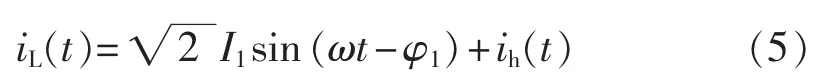
考虑到消除负序、谐波和无功，结合式（3）和（4），α、β端口电流的期望值设为：

在一个电源周期内，电源提供的能量应为负载消耗的能量与IPFC损耗的能量之和，即：

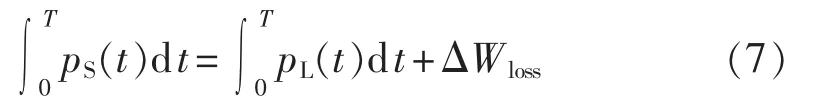
其中，pS=uα（t）isαr（t）+uβ（t）isβr（t），为电源输出瞬时功率；pL（t）=uα（t）iL（t），为负载瞬时功率；ΔWloss为 IPFC损耗的能量。

将式（4）—（6）代入式（7），可得：

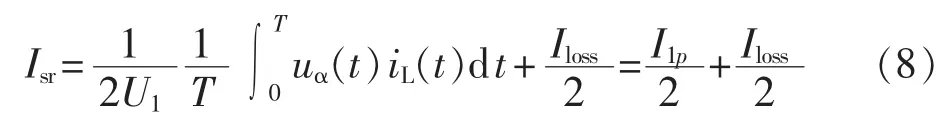
其中，T为电源周期，I1p=I1cosφ1，为负载电流有功分量；Iloss为ΔWloss对应的损耗电流分量。所以，IPFC两端口补偿电流期望值为：

2 IPFC的控制策略

为提高IPFC补偿装置的综合补偿性能，本文在传统电压外环、电流内环控制方法的基础之上，基于均值滤波算法，提出了直流侧电压PI均值前馈控制和直流侧电流均值前馈控制策略，有效地提高了系统的动态特性及稳定性，减小了稳态误差，构建出如图3所示的IPFC控制系统框图。鉴于滞环比较具有动态响应快、鲁棒性好等优点，满足同相供电IPFC的要求[9]，因此电流内环采用滞环比较控制策略。两变流器分别单独控制，通过β侧变流器闭环PI控制稳定直流侧电容电压，以直流侧电压PI均值前馈控制稳定α、β侧指令参考电流，以直流电容电流均值前馈控制改善动态特性及稳态误差，达到了良好的综合性能。

图3 IPFC控制框图Fig.3 Block diagram of IPFC control

2.1 直流侧电压PI均值前馈控制

考虑IPFC电路结构，当忽略电路损耗时，根据瞬时功率平衡原理，可得：

由于机车负载谐波电流主要表现为奇次谐波，由式（9）可得变流器交流侧电流为：

其中，I11为负荷有功电流的一半，I12为负荷无功电流，Im为谐波电流，φm为谐波电流初相位。

将式（4）和（11）代入式（10）可得：

由式（12）知，等式右侧均为偶次谐波。故uC可表示为：

uC的脉动频率为偶次倍频，波形接近正弦波。所以可采用2倍频均值算法（即图3中“均值1”模块）滤除脉动分量，得到IPFC损耗电流Iloss。为降低直流偶次脉动频率及脉动频率对交流环节的影响，常在直流环节并入LC滤波器组，如图4所示。

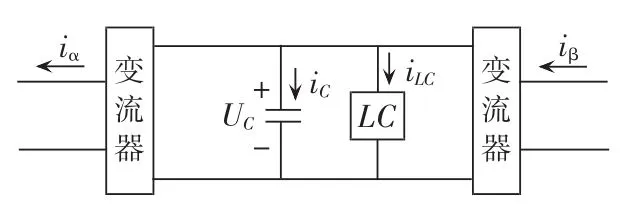
图4 直流环节结构Fig.4 Structure of DC link

2.2 直流侧电流均值前馈控制

根据图2和图4，对直流环节列写KCL方程可得：

电路达到稳定时，可得：

从式（15）可看出，除iC项外，其余项为基波和奇次谐波，故通过直流电容电流工频均值算法（即图3中“均值2”模块）实现LC滤波器组的前馈控制，提高了系统的动态特性，减小了稳态误差。

3 仿真分析

为证明本文所提控制方法的正确性，建立了基于MATLAB/Simulink的仿真模型。IPFC参数为k=10，L=1 mH，C=5 mF，直流侧电压给定值为Uref=5 kV。牵引网电压为 27.5 kV，负载电流[9]iL=200 sin（ωt-36.8°）+42 sin（3ωt-60°）+30 sin（5ωt+150°）A，其中3次、5次谐波含量分别为21%、15%，功率因数为0.8（滞后），容量为4800 kV·A。再生制动时电流取为-iL。

原、副边电流仿真波形如图5所示。由图5（a）可见，iα、iβ呈较标准的正弦波，幅值大小相等。对比图5（b），传统控制方法得到的正弦波发生明显畸变，幅值大小不等。α、β侧电流反馈至三相电力系统的电流波形如图 5（c）、（d）所示。 易见，图 5（c）中原边三相电流有较好的对称性，而传统控制方法波形（见图5（d））对称性较差。进行傅里叶分析，得到2种控制方法下原、副边电流基波值及谐波含量见表1。

图5 2种控制方法下原、副边电流波形Fig.5 Waveforms of primary and secondary currents for two control schemes

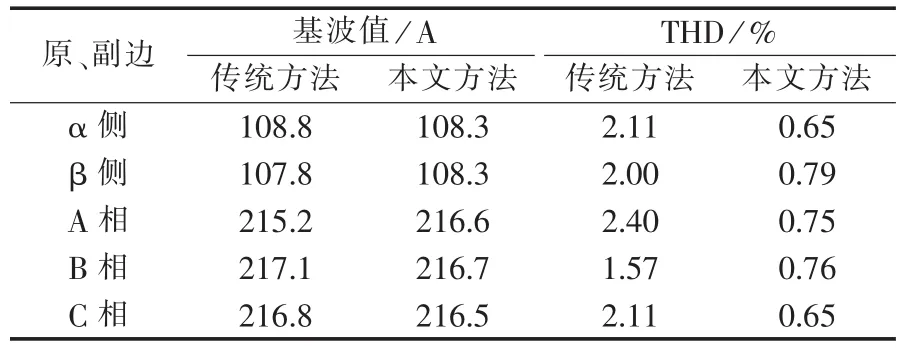
表1 原、副边电流的傅里叶分析Tab.1 FFT analysis for primary and secondary currents

从表1可以看出，通过本文控制方法得到的电流谐波含量低，α、β侧及原边A、B、C相的谐波畸变率THD均降到0.8%以下，且原、副边各相基波值近乎相等。而传统控制方法不仅谐波含量远高于0.8%，各相基波大小也存在一定差异。所以，本文控制方法在抑制谐波、改善波形对称性方面有明显的优势。

图6为采用2种方法得到的直流侧电压波形。可见，本文控制方法中，电压在0.1 s时趋于稳定，到0.25 s时，电压变化量仅为15 V，稳态误差很小；而传统控制方法中，电压在0.1 s及以后时刻仍处于波动，到0.25 s时的波动量达300 V。所以，本文控制方法有效增强了系统的动态特性和降低了稳态误差。

图6 直流侧电压Fig.6 DC link voltage

图7反映了再生制动时直流侧电压情况。0.25 s时列车由牵引状态过渡至再生制动状态，经过约0.05 s电压再次达到稳定。状态转换过程中并未对直流电容造成过大的电压冲击。图8为三相电力系统由牵引状态过渡到制动情况下的电流波形。可见，在制动工况下，本文控制方法有较好的适应性。

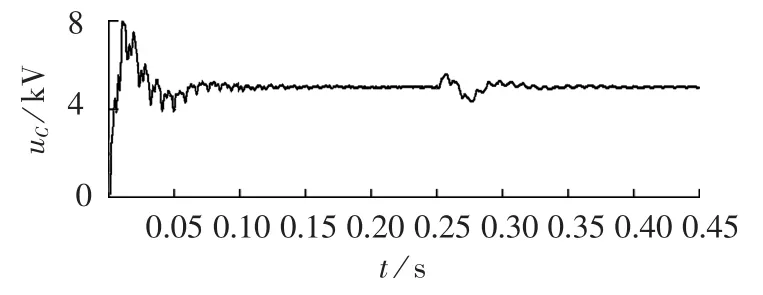
图7 再生制动时直流侧电压Fig.7 DC link voltage of regenerative braking

图8 再生制动时原边电流Fig.8 Primary current of regenerative braking

4 结论

为解决电气化铁道的谐波、无功、负序及电分相等问题，本文研究了Scott变压器与IPFC构成的同相供电系统，重点探讨了IPFC的控制策略。在传统控制方法基础之上，提出直流侧电压PI均值前馈控制和直流侧电流均值前馈控制策略，有效实现了谐波、无功、负序的补偿，稳定了直流侧电压，提高了系统的动态特性及稳定性，减小了稳态误差，对改善电气化铁道牵引供电系统电能质量、取消电分相起到积极的作用。