基于双重水印加密和SVD的视频水印方案

张 燕

（商洛学院 数学与计算机应用学院，陕西 商洛 726000）

基于双重水印加密和SVD的视频水印方案

张 燕

（商洛学院 数学与计算机应用学院，陕西 商洛 726000）

针对视频水印的安全性，提出了一种基于双重水印加密和SVD的视频水印方案。该方法首先将水印图像经Arnold置乱，对置乱后的水印通过Chebyshev混沌映射进行加密,保障水印的安全性；然后，对视频关键帧进行三级小波分解，利用SVD对几何失真的不变性，将水印3次嵌入到LL3、HL3和LH3中。实验表明该方案对高斯噪声、MPEG压缩、剪切等具有较高的鲁棒性。

视频水印；Arnold变换；混沌映射；小波分解；奇异值分解

近年来多媒体应用以惊人的速度在发展，大量的数字化产品得到了广泛的使用与传播，盗版和知识产权保护变得日趋严峻，因此数字产品的信息安全和版权保护等成为人们高度关注的问题。目前，数字水印技术已成为国际信息安全学术界研究的一个前沿方向，这就为数字产品的安全传播、保存等开创了一条全新的道路。而其中的数字视频水印技术作为有效的保护视频作品版权的手段受到人们广泛的关注和重视，并在信息安全和多媒体处理领域成为一个研究热点。

然而，由于一些数字水印技术没有采取加密措施或者加密措施比较简单，非授权者可以通过一些计算操作很容易检测或提取出嵌入的数字水印，并进行篡改，从而影响水印的安全性。目前出现了很多基于混沌的图像加密技术为数字图像的加密提供了新的思路。文献[3-4]的混沌加密方法均是将混沌序列采用阈值法进行二值化，而文中采用一种新的二值化方法，首先将混沌序列变为二进制，然后将二进制按照某种策略进行二值化，再与置乱后的水印图像进行异或运算来实现对水印图像的加密。

由于小波分解具有多分辨率的特征，而图像奇异值对几何失真又具有稳定性，因此出现了许多DWT-SVD(小波变换-奇异值分解)的水印算法。文中以二值图案作为水印，首先对原始视频关键帧图像进行三级小波变换，依据子图特点，将水印嵌入到垂直子图、水平子图和近似子图中。对嵌入水印的子图和加密后的水印图像同时进行分块，并对每一块进行SVD分解，然后在嵌入水印的区域中分别嵌入对应水印的S对角矩阵，完成水印的3次嵌入。

1 视频水印算法

1.1 Arnold置乱变换

Arnold[1]变换俗称“描脸变换”,它是通过对图像中像素的位置或者是像素的颜色等做变换，来“扰乱”图像，因此在一定程度上能达到迷惑第三者的目的。对于一幅大小为N×N的图像，Arnold变换运算如式(1)所示,其中，N是矩阵的大小，(x,y), (x',y')、表示像素点在变换前后的位置，位置移动实际上是对应点的灰度值或RGB颜色值的移动。

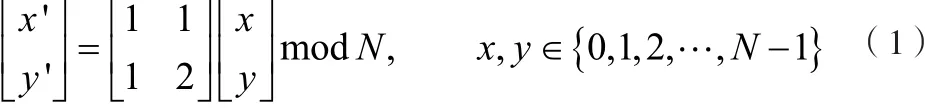
Arnold变换有一定的周期性，当迭代的使用Arnold变换对图像进行置乱，当迭代到某一步时就会重新得到置乱前图像。本文嵌入的水印是二维二值图案，同时还由于Arnold变换的时空复杂度比较低，故采用Arnold对水印图像进行置乱变换。

文中使用的水印为128*128的二值图案，如下图1所示，(a)是原始水印图案，(b)是对原水印图案进行23次Arnold变换得到的图像。

图1 预处理水印图像Fig. 1 Pretreatment watermark image

为了使嵌入的水印具有良好的保密性同时也加强了水印图像对剪切等处理的抵抗性，将图像分成大小为64*64的5块。

1.2 基于混沌序列的图像加密算法

混沌现象是发生在一个确定系统的伪随机过程，系统在某个参数和给定的初始条件下，其运动是确定的。使用混沌动力系统产生的混沌序列具有可控的低通性和很好的相关性。混沌序列对初始条件极为敏感。混沌函数具有伸大拉长和折回重叠的性质，因此产生的序列有很好的保密性，而且密钥的管理简单、安全。

目前，对水印进行混沌加密[2][3]的方法主要有Reny映射、Logistic映射、Chebyshev映射和花托自同构，而水印加密算法的好坏与所采用的混沌映射方法有着密切的关系。通过比较，在初始值均相同的情况下，Logistic的参数值选择接近某一极限的条件下，可知Chebyshev映射的加密效果比Logistic映射的加密效果好，因此本文选用Chebyshev映射产生混沌序列。

通过Chebyshev映射产生混沌序列，将这些序列转化成与水印大小相同的二值矩阵，再与置乱后的水印进行异或运算，实现水印的加密。加密算法如下：

1 ) 对大小为m*n的二值水印图像进行Arnold变换，并将水印图像置乱次数作为密钥保存起来。

2 ) 利用Chebyshev映射产生长度为(m*n)/4+k的混沌序列，其中，k为大于1的整数。

3 ) 将混沌序列转化成与水印大小相同的二值矩阵。

4 ) 将二值矩阵与置乱后的水印进行异或运算，得到加密后的水印。

上述算法如果无法全部得知置乱次数和置乱初始位置、混沌映射的初值和k，则无法正确解密水印，因此进一步保证了水印的安全性。

1.3 小波变换

近年来，将小波变换用于图像处理中已成为重点和热点，其基本思想是将图像进行多分辨率分解，图像在不同空间、不同频带被分解成四个子图4，即水平方向HL子图、垂直方向LH子图、对角方向HH子图和低频LL近似子图，如果还需要继续对图像进行小波变换只需要对低频LL进行分解就可以得到下一级小波分解，依次类推，可以进行多级小波分解。

本文选取的视频关键帧的每帧大小为256*256，水印选用二值图案，每块大小为64*64，选择Haar小波作为小波基函数，将关键帧图像进行三级小波变换。

1.4 分解图像的奇异值

奇异值分解(SVD)[5-7]是一个矩阵对角化的数值方法，给定一个大小为m*m的实数矩阵A，其可分解为3个矩阵：

其中，U、V是大小为m*m的正交矩阵；S为对角矩阵。对角矩阵S中的特征值是按大小有序排列的。

SVD具有的一些特性在图像处理中有十分广泛的应用。图像奇异值分解的主要特征有：

1）能将大量的信号能量快速压缩到很少的系数中，奇异值表现出的是图像的固有特征而不是视觉特征，保障了水印的不可见性。

2）数字图像的特征值很稳定，图像经常规处理后，其特征值变化微小，这样将水印嵌加到特征值中有比较好的鲁棒性。

1.5 视频水印域的选择

依据视频相邻帧间存在的相关性[8]，使用了文献[1]中的方法提取视频关键帧，该方法是一种基于小波变换的运动估计方法，首先对视频帧进行小波变换，由低频系数判断每一帧的画面背景，高频系数判断画面细节；将相邻帧小波系数差值与阈值比较，提取出相同场景和不同场景的视频关键帧，然后将水印嵌入到关键帧中。

1.6 水印嵌入过程

水印嵌入思想是将视频划分为多个不同的场景，在同一场景中，将多个置乱及加密后的水印中的某一块，嵌入到每个关键帧的Y通道中；在不同的场景中嵌入完整的置乱及加密后水印。水印嵌入过程如图2所示。步骤如下：

1 )RGB转换成YUV，提取关键帧图像的Y通道；

2 )对关键帧图像进行三级小波变换，得到HL3、LH3和LL3作为嵌入水印区域；

3 )以大小为8*8对加密后的水印和HL3、LH3、LL3三部分分别进行分块；

4 )对每一块进行SVD分解，获得水印各块的对角矩阵Swi,j，LH3的对角矩阵Shi,j，HL3的对角矩阵Svi,j和LL3的对角矩阵Sai,j以及它们对应的U,V矩阵。

5 )利用公式(2)所示,将水印嵌入到 LH3、HL3 和LL3 3个子图中。

其中，Sk(i,j)表示 Shi,j、 Svi,j、Sa(i,j)，SIk(i,j)表示 Shi,j、Svi,j、Sa(i,j)嵌入水印后的对角矩阵；ak表示嵌入水印的强度，为了使水印的鲁棒性和不可见性得到平衡，3个区域中嵌入的水印强度是不同的。

6 )利用式(1),对加密后的水印和LH3 、HL3 、LL3 的各块进行SVD重构，将各块还原为一个整体。

7 )对小波系数进行逆变换得到嵌入水印的Y通道视频水印图像Iw ，再将Y通道与其它两个通道融合，得到嵌入水印的完整图像，再将图像从YUV变换到RGB，得到嵌入水印后的图像。

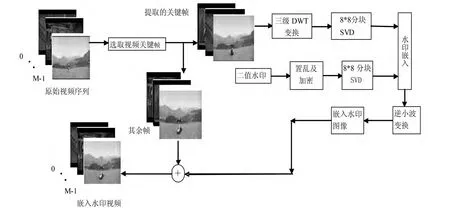
图2 视频水印嵌入算法流程图Fig. 2 Video watermark inserting algorithm frame chart

1.7 水印提取过程

水印提取与水印嵌入过程正好相反，需要原始视频图像。步骤如下：

1 )将嵌入水印后的视频帧图像转换到YUV色空间；

2 )将嵌入水印后的关键帧视频图像和原始关键帧视频图像分别进行三级小波分解，得到LH3W、 HL3W、 和LL3W、LH3 、HL3、LL3 6 个子图；

3 )对6个子图进行8*8分块，再对每一块进行SVD分解，得到各奇异值 、Sk,其中 为待提取水印得到的特征值， Sk为原始图像得到的特征值；

4 )采用公式(3)得到3组图像的水印值；

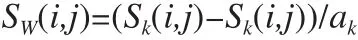
5 )根据公式(1)对水印的各块进行SVD重构，得到完整的水印；

6 )对提取的水印信息根据水印加密、置乱的逆运算，得到原水印图案。

2 性能测试及分析

实验选择一段118秒视频，选取的关键帧的每帧大小为256x256。水印选用的是每一块大小为64x64的二值图案，选择haar小波作为小波基函数，实验采用Matlab7.1进行仿真。

2.1 不可见性测试

水印嵌入到视频当中，要保证视频的质量，即从视觉上无法感知到水印的存在。如图3所示，可以看出原关键帧视频图像和嵌加水印后的关键帧视频图像质量几乎没有下降，说明本文算法的不可见性和可逆性效果比较好。

图3 原始视频帧图像和含水印视频帧图像Fig. 3 The primitive video frame image and contains the watermark video frame image

2.2 鲁棒性测试

2.2.1 加 噪

在所有水印攻击中，最常见的一种方法就是加噪，视频在网络传输中被噪声攻击是在所难免的，所以提高含水印视频抗噪声干扰是非常重要的，如图4所示是对视频序列增加高斯噪音1%-10%的实验结果。

图4 高斯噪音攻击实验结果Fig. 4 Gauss noise attack experimental result

随着加入高斯噪音强度不断增加，视频图像的质量明显下降，当所加高斯噪音超过4%时，视频图像的质量已经很差，但仍能提取出较清晰的水印，而当高斯噪音超过8%时，视频图像的质量已经很是无法容忍了,如图5(a)，但仍能检测出水印图案的存在，如图5(b)。

图5 噪音攻击后图像与提取的水印Fig. 5 After noise attackimage and extraction watermark

2.2.2 剪 切

剪切也是对水印的一种攻击,如图6所示，通过剪切掉一部分图像来破坏隐藏的水印，还是可以提取出水印图像，说明这种方法对剪切具有很好的鲁棒性。

图6 被剪切的含水印视频帧图像Fig. 6 Contains the watermark video frame image by cut

2.2.3 视频压缩

对加入水印的视频流进行了不同压缩比的MPEG压缩攻击,如图7所示是含水印视频在压缩率30%后重建的图像。实验结果表明，只要压缩效果在视觉上能接受，即在没有明显产生块效应的情况下，都能检测到水印的存在，而即使在重建图像出现了明显的块效应，算法仍能检测到水印的存在。

图7 压缩率30%攻击后重建视频图像Fig. 7 After compression ratio 70% attacks,reconstruction of video image

3 结 论

文中提出了一种基于小波域的视频水印算法并对水印进行了双重加密以及将奇异值分解应用到视频水印中。该算法具有以下特点：

1 )对二值水印图像进行双重加密，首先采用Arnold置乱对水印进行第一层安全性保护，由于Arnold变换简单易行，变换周期小，安全性较低，因此进一步对置乱后的水印采用Chebyshev混沌映射进行加密，为水印的安全性提供了第二层保护。2)将水印图像嵌入到2个细节子图中提高了图像对噪声、压缩等攻击的抵抗力，将水印图像嵌入到近似子图中，确保了水印的安全性。

文中对噪声、压缩、剪切有较好的稳定性，以后将JPEG压缩、帧旋转、帧删除等方面研究其稳定性。

[1] 张燕,朱俊平.基于小波域和图像融合技术的视频水印算法研究[J].微计算机信息,2010,27(5):174-176.

ZHANG Yan,ZHU Jun-ping. Research on the digital watermarking video algorithm based on waveletsdominand image fusion[J].Microcomputer Information,2010,27(5):174-176.

[2] 秦海,孙刘杰.基于Arnold置乱自适应图像数字水印算法[J].微计算机信息,2010,26(10).

QIN Hai,SUN LIU-Jie.Adaptive Image watermark algorithm based on arnold transformation[J].Microcomputer Informati on,2010,26(10-2):208-209.

[3] 杨格兰,张建明.基于混沌序列的二值图像加密算法[J].计算机技术与发展,2006,16(2):148-150,153.

YANG Ge-lan,ZHANG Jian-ming.Binaryimage encryption algorithm based on chaotic sequences[J].Computer Technology and Development,2006,16(2):148-150.

[4] 刘剑鸣,李晓君.基于小波域的模糊混沌水印算法[J].计算机工程,2011,37(8):132-134.

LIUJian-Ming,LI Xiao-Jun.Fuzzy chaotic digital watermark algorithmbased on wavelet domain[J].Computer Engineering,2011,37(8):132-134.

[5] 薛胜男,陈秀宏.基于混沌加密和SVD的数字图像水印算法[J].计算机工程,2010,38(19):107-110.

Xue Sheng-Nan,ChenXiu-Hong.Digital Image Watermarking Algorithm Based on Chaos Encryption and SVD[J].Computer En gineering,2010,38(19):107-110.

[6] 张秋余,李凯.基于混沌和SVD-DWT的稳健数字图像水印算法[J].计算机应用研究,2010,27(2):218-220

ZHANG Qiu-Yu,LIKai.Robust digital image watermarking algorithm based on chaos and SVD-DWT[J].Application Research of Computer,2010,27(2):718-720.

[7] 侯一民， 孙嘉兵， 张宇. 基于小波包降噪和Hilbert谱奇异值的滚动轴承故障诊断[J]. 陕西电力，2013（11）：41-44.

HOU Yi-min，SUN Jia-bing，ZHANG Yu. Fault diagnosis of rolling bearing based on wavelet packet denoising and hilbert spectrum singular value decomposition [J]. Shaanxi Electric Power，2013（11）：41-44.

[8] DU Yao-gang,YAO Wen.Research and implementation of video watermarking algorithm[J].Computer Simulation,2011(2):144-146.

Video watermarking scheme based on dual watermark encryption and SVD

ZHANG Yan
（School of Mathematics and Computer Application, Shangluo University, Shangluo 726000, China）

According to the security of video watermarking,a video watermarking scheme based on dual watermark encryption and SVD is proposed. Firstly, scrambling the watermark image, after the scrambling watermark through Chebyshev chaotic mapping is encrypted, guarantee the security of the watermark; then, the video key frames conduct three wavelet transform, Using SVD invariance of geometric distortion, the watermark is embedded into LL3, HL3 and LH3, 3 times. Experimental results show that the algorithm has good robustness to noise attack 、MPEG compression and shear.

arnold transform; chaotic mapping;wavelet transform;singular value decomposition

TN918.91

A

1674-6236(2014)14-0128-04

2014–04–11 稿件编号：201404112

陕西省教育厅科学研究计划项目(12JK0747);陕西省教育厅科学研究计划项目(2013JK1201) ;商洛学院自然科学研究项目(13SKY024)

张 燕(1977—)，女，陕西丹凤人，硕士，助教。研究方向：信息安全、计算机网络应用。