不确定环境多目标投资组合模型及求解算法探究
钱淑渠, 韩燕飞,李晓丽
(安顺学院 数理学院,贵州 安顺 561000)
不确定环境多目标投资组合模型及求解算法探究
钱淑渠, 韩燕飞,李晓丽
(安顺学院 数理学院,贵州 安顺 561000)
考虑投资市场的随机动态属性,以Markowitz均值-方差模型为基础,建立了一种不确定环境多目标投资组合模型,模型中以天为时间单位,通过预先设定的采样周期计算当前时刻的收益率和方差而获得时变的投资组合模型。利用一种动态多目标免疫优化算法对模型进行实证分析,选取深沪300中的23种资产(2009年1-2月份)的实际日交易数据进行实验,结果表明:算法能跟踪不同时刻的收益-风险Pareto有效面,且采样周期的选取对相同风险下的收益具有一定的影响,此结论对投资组合理论的进一步研究具有一定价值。
投资组合模型;多目标优化;免疫算法;Pareto有效面
不确定投资组合问题即在瞬息万变的投资市场环境,如何实时分配有限资金,使投资收益(Return)最大、风险(Risk)最小。早在1952年,Markowitz提出了一种静态的均值-方差模型(M-V)[1],该模型使得投资风险首次被量化,奠定了投资组合理论的研究基础。继后,大量静态投资组合模型及其相应的求解算法被提出:Chen等[2]基于直观模糊优化方法提出了M-V非对称模糊选择模型,并利用matlab软件求解;Huang等[3]引入一种股票scoring机制利用模糊函数计算股票得分,进而对投资组合资产进行排序选择,获得一种新的模糊组合模型,并用遗传算法对模型求解,研究了算法求解模型的有效性;Kawakami等[4]以信息率为目标函数研究了遗传算法对M-V模型求解的有效性; Mishra等研究了多目标进化算法在金融投资领域中的应用,并以股票投资组合问题为实例研究的算法求解的实用性;Anagnostopoulos等研究了5种著名的多目标进化算法(MOEAS, NPGA2,NSGAII,SPEA2,e-MOEA)对约束M-V模型的求解的优越性。其他参见文献[5]。
实际上,投资市场的不确定属性决定了投资组合问题属一类不确定环境问题,已有的模型均在理想市场环境下获得的一种静态优化模型,不能较真实的反应现实中的不确定投资环境,且投资者往往不仅对某一种投资组合感兴趣,而希望得到不同时刻的一系列风险-收益的投资组合,此决定了投资组合模型是一类不确定多目标优化问题,不同风险-收益点对构成多目标问题的pareto有效面,已有的数学规划法均将多目标问题化为单目标问题求解,经过选择不同权重系数而获得pareo有效面,算法计算量较大,为了克服此缺点,故需要设计更高级的优化算法。近来,大量的学者论证了遗传算法对投资组合模型求解的有效性, 但遗传算法固有的局部收敛特征使得其不适应求解该类复杂NP-hard问题,而免疫算法其群体多样特性、强探索和开采能力使得其适合投资组合问题的求解,该领域的相关研究在国内外还极为罕见,本研究组近年在该领域已做了部分初步探究,获得部分成果[6-7]。故文中在Markowitz的M-V模型的基础上,建立不确定多目标投资组合模型 (DMPM)并利用本研究小组已设计的不确定多目标免疫优化算法 (DMIOA)[8]对模型求解。数值实验中,选取深沪300的23中股票从2009年1月5日至2009年2月3日3周内日收益率进行实证分析,实验表明模型的合理性及算法的优越性。
1 不确定多目标投资组合模型
1.1 收益风险函数
对于不确定投资组合问题,取采样周期为p天,估计t∈Z+时刻的收益和风险,如图1所示。
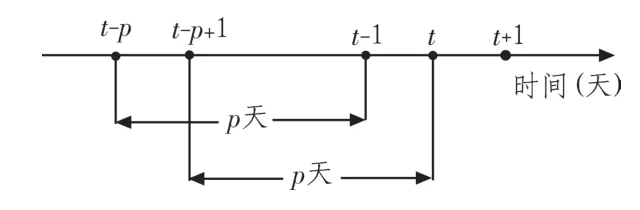
图1 风险和收益的采样方法示意图Fig.1 The sample method of risk and return
设市场有n种可交易的风险资产,资产i在t时刻之前 p天的收益率分别为
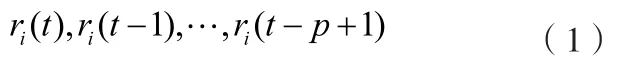
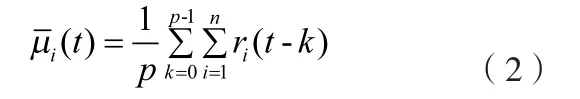
第i种风险资产t时刻的方差
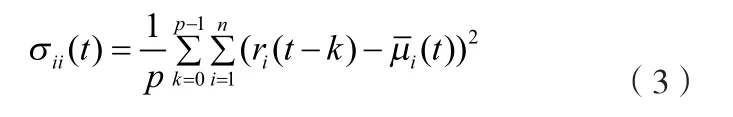
第ik两种风险资产t时刻的协方差
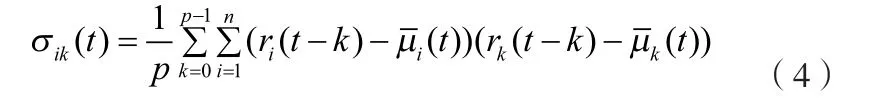
设Xi为第i种风险资产的投资比率,则资产i在t时刻前p天的收益分别为
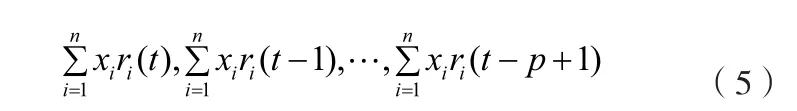
则p天风险资产的期望收益
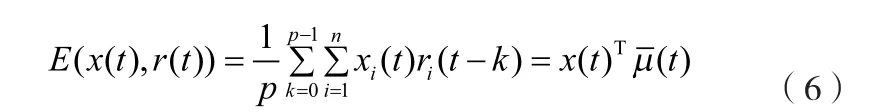
相应的方差为
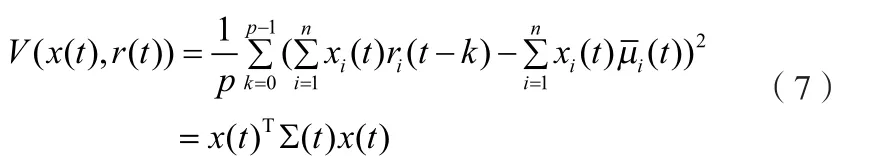
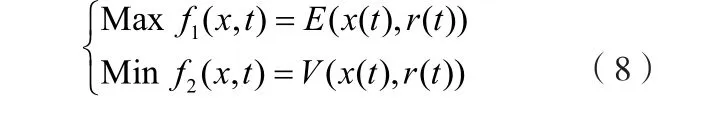
1.2 约束条件
因为X为t时刻投资比率,故为了满足投资者的预算需求,有

一般情况下考虑不允许卖空,则有
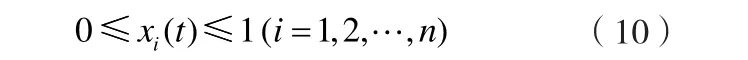
投资者在投资的过程中还会考虑到每一种资产的最大和最小投资比率,以便分散投资,即有
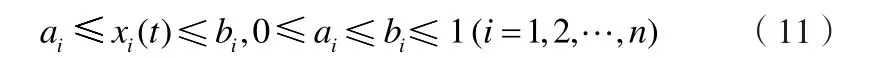
式(8)(9)(10)即为Markowitz的均值-方差模型,在此引入投资比率的约束(11)。
由式(8)~式(11)构成一种约束不确定多目标投资组合模型(DMPM)。
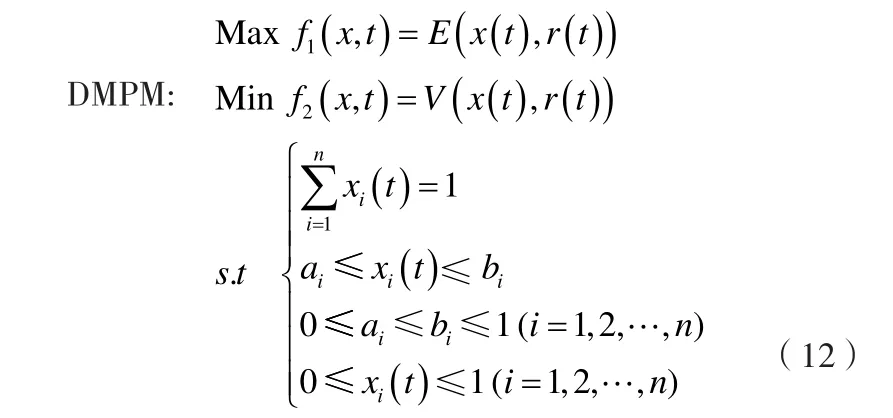
2 实证分析
根据所建立的不确定多目标投资组合模型,投资管理者往往希望快速获得不确定市场环境下分布较好的风险-收益Pareto有效面以供其按自己的偏好作出不同时刻的最优决策,故为了将模型用于实际,获取2009年1月5日至2009年2月3日发布的深沪300的23种风险资产(深发展A,深能源A,中兴通讯,长城电脑,深圳机场, TCL集团,美的电器等)3周内的日收益率(如表1)进行实证分析,由于篇幅的限制,在此仅列出4个时刻的实验结果。
选取本研究小组已设计的算法DMIOA[13]对所建立的不确定多目标投资组合模型进行求解,算法中参数λ = 0.03,β =2.5,m0= 5,算法的初始群规模N = 80,指定算法所获Pareto解集的最大规模N0= 80,算法最大迭代数 G = 200。
模型DMPM中参数a1= 0.5,b1= 0.75,以2009年1月5日为初始天,根据式(1)依次获得1月16日(t=1),1月19日(t=2),2月3日(t=8)期望收益率及资产间的方差协方差矩阵,应用算法DMIOA所获不同采样周期下不同时刻Pareto有效面为图2~图5。
特别指出,DMIOA中环境识别依据下式确定环境t是否存在相似环境
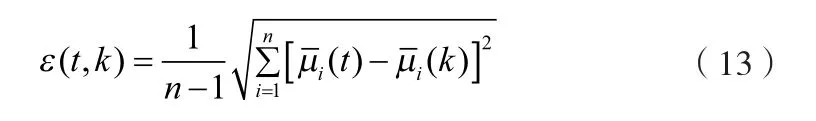

表1 选取深沪23种风险资产3周内日收益率Tab.1 Return rate of 23 assets of Shenzhen and Shanghai stock
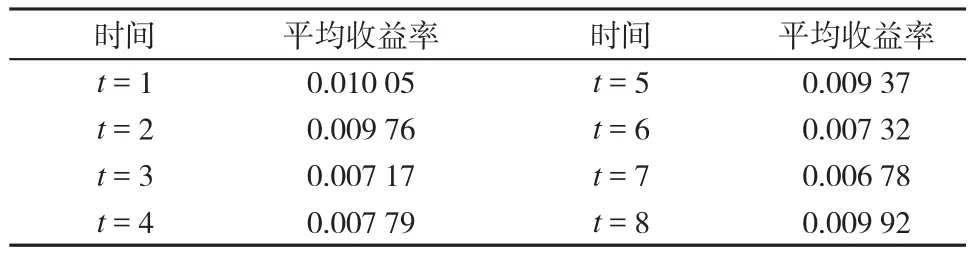
表2 不同时刻23种资产的平均收益率Tab. 2 Average return of 23 assets in difference time
图2~图5为取不同采样周期所获得t由1~4时刻的风险-收益Pareto有效面。首先,对于同一采样周期,从不同时刻所获Pareto有效面分析,由图2获知,当采样周期p=5天时,算法在4个时刻均能获得有效的Pareto有效面,在t=2和t=3两个时刻算法所获风险-收益Pareto有效面范围非常窄,当两时刻风险分别大于0.6×10-3和0.85×10-3时,不能获得风险-收益Pareto有效面,特别在t=3时相对于其他时刻在相同的风险下所获的收益非常低,此由表2可以看出,此时刻资产的平均收益率较低,影响了资产的总投资收益,表2中t=1、2两时刻资产平均收益率较高,对应于图2中此两时刻所获风险-收益Pareto有效面分布范围非常广,此能给投资者更多的选择余地,此表明算法能根据时间的变化跟踪不同时刻的Pareto有效面;同样由图3~图5获相似结论。
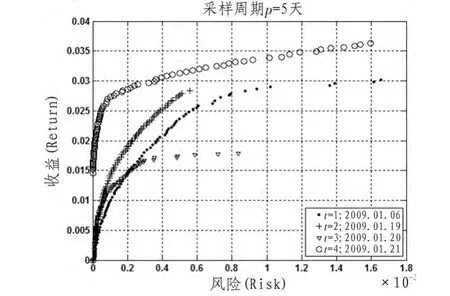
图2 采样周期p=5时DMIOA在1~4时刻所获风险-收益Pareto有效面Fig.2 The Pareto-optimal front of risk-return obtained by DMIOA with p=5 form 1 to 4 time
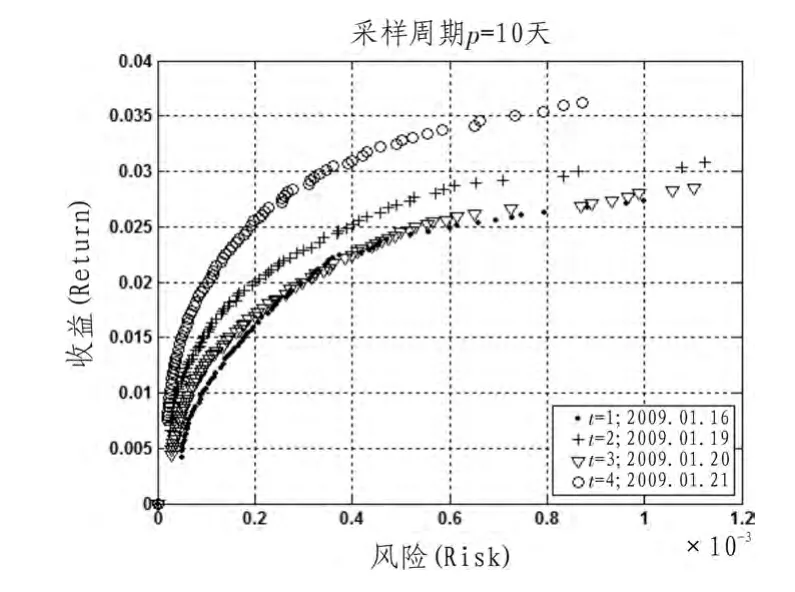
图3 采样周期p=10时DMIOA在1~4时刻所获风险-收益Pareto有效面Fig.3 The Pareto-optimal front of risk-return obtained by DMIOA with p=10 form 1 to 4 time
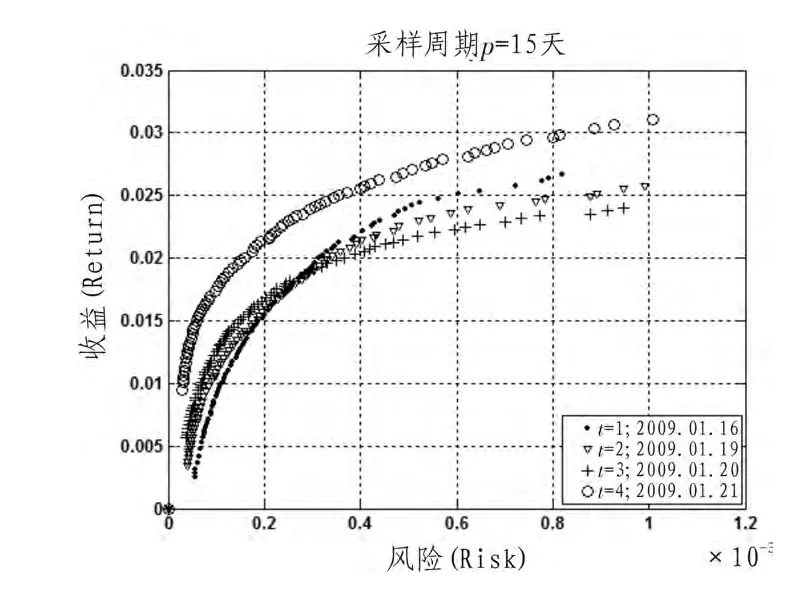
图4 采样周期p=15时DMIOA在1~4时刻所获风险-收益Pareto有效面Fig.4 The Pareto-optimal front of risk-return obtained by DMIOA with p=15 form 1 to 4 time
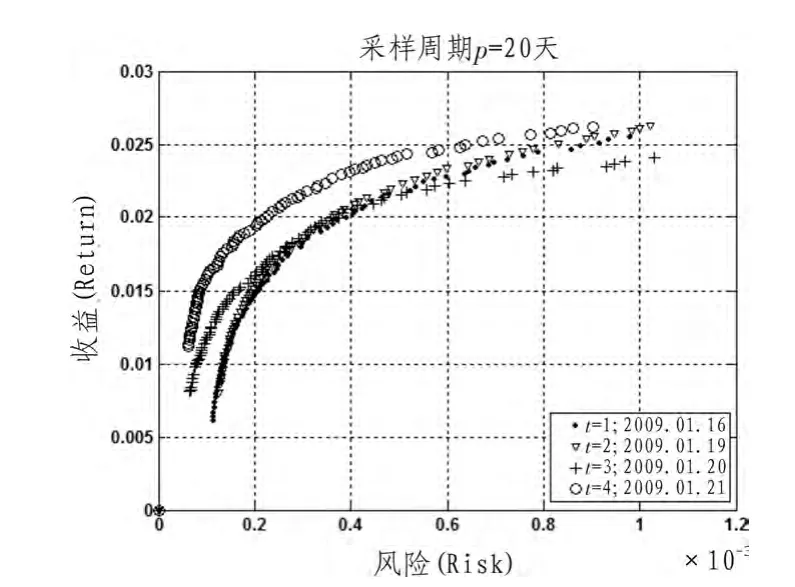
图5 采样周期p=20时DMIOA在1~4时刻所获风险-收益Pareto有效面Fig.5 The Pareto-optimal front of risk-return obtained by DMIOA with p=20 form 1 to 4 time
其次,从不同采样周期分析,由图2~5获知,对于同一时间,采样周期不同,所获的Pareto有效面不尽相同,由所有图获知,对于t=1、2、3、4时,采样周期p=10天时所获Pareto有效面较好,对于同一风险下所获的收益较大(如当风险为0.8×10-3时,采样周期p=10天在t=1时所获收益大于0.035,在t=2、3、4时所获收益均大于0.025,而其他采样周期下在t=1时收益均小于0.35,在t=2、3、4时收益或小于0.025或比0.025稍大),且Pareto有效面分布较均匀,而其他采样周期下稍差,此表明投资组合的收益预测受采样周期的选取影响。
综上,算法DMIOA在不同时刻均能获得相应的风险-收益Pareto有效面,当取不同采样周期时所获Pareto有效面效果不尽相同,由实验可知,当取采样周期p=10时在不同时刻所获风险-收益Pareto有效面较好,对于相同的风险下所获收益较大。
3 结 论
文中考虑实际市场投资环境,建立一种不确定多目标投资组合模型,并用利用不确定多目标免疫优化算法对模型求解,选取23种投资资产历史数据仿真分析,表明不确定投资组合模型较静态投资模型更能体现实际投资市场,有利于进一步指导投资者如何选择恰当的投资市场环境,提高投资效益,对投资组合理论研究提供了新的研究方向。接下来还需进一步考虑其他市场环境,建立更合理的不确定投资组合模型及其求解算法的研究工作。
[1] Markowitz H.Portfolio selection[J],Journal of Finance,1952,1(7):77–91.
[2] Chen GH, Luo Z J, Liao X L. Mean variance skewness fuzzy portfolio selection model based on intuitionistic fuzzy optimization[J]. Procedia Engineering, 2011(15):2062-2066.
[3] Huang C F, Chang C H,. Chang B R,et al. A study of a hybrid evolutionary fuzzy model for stock selection[C] //2011 IEEE International Conference of Fuzzy Systems, Taipei,2011:210-217.
[4] Kawakami A , Orito Y, Inoguchi M , et.al. Dynamic asset portfolio optimization by using genetic algorithm[J]. Information and Systems, 2009 ,129(7):1348-1355.
[5] Zheng J.G, Zhou L.Multi-objective model for uncertain portfolio optimization problems[J]. International Journal of Advancements in Computing Technology,2011,3(8):138-145.
[6] 钱淑渠, 武慧虹. 约束多目标投资组合模型及其求解算法研究[J]. 计算机仿真.2011, 28(10): 389-392.
QIAN Shu-qu,WU Hui-hong. Study of constrained Multiobjective Portfolio model and solving algorithm[J]. Computer Simulation, 2011, 28(10):389-392.
[7] 钱淑渠, 武慧虹. 动态环境模糊投资组合模型求解研究[J]. 安顺学院学报, 2012, 14(1):114-117.
QIAN Shu-qu, WU Hui-hong. Fuzzy portfolio model and solving in dynamic environment[J]. Journal of Anshun University, 2012,14(1):114-117.
[8] 钱淑渠, 张著洪. 动态多目标免疫优化算法及性能测试研究[J]. 智能系统学报, 2007,2(5):68-77.
QIAN Shu-qu, ZHANG Zhu-hong. Dynamic multi-objective immune optimization algorithm and study on performance Test[J].CAAI Transactions on Intelligent Systems, 2007,2(5):68-77.
Study of uncertain environment multi-objective portfolio model and solving algorithm
QIAN Shu-qu, HAN Yan-fei, LI Xiao-li
(School of Mathematics and Physics Science, Anshun University, Anshun 561000,China)
A uncertain multi-objective portfolio model that based on Markovits mean-variance model is proposed,which considers the time-changing nature of the problem emerges from the fact that market conditions and asset performance change continuously, the model unit of time in days, the return rate and variance are obtained by predetermined sampling period. the existing immune optimization algorithm for dynamic multi-objective empirical is used to analysis the performance of the model, Selecting the actual data of 1-2 months transaction of the 23 kinds of assets of Shanghai and Shenzhen 300 in 2009, results show that: the algorithm can track the dynamic Pareto efficient frontier, and the return is effected by the sampling period, the conclusion of the experience has a certain reference value for further theory research of portfolio.
portfolio model; multi-objective optimization; immune algorithm; Pareto efficient frontier
TN911.2
A
1674-6236(2014)14-0013-04
2014-03-17 稿件编号:201403172
贵州省科学技术基金项目资助(黔科合J字[2012]2002号);安顺学院SRT项目资助(2013SRT03)
钱淑渠(1978—),男,安徽枞阳人,硕士,副教授。研究方向:智能优化算法、数学建模。

