基于计量模型的NBA篮球成绩影响因素分析

黄晓敏

（天津大学 天津 300072）

基于计量模型的NBA篮球成绩影响因素分析

黄晓敏

（天津大学 天津 300072）

美国NBA篮球联赛深受广大群体喜爱，对篮球这项体育运动有着重要影响，因此对于NBA球员的数据分析很有意义。文中首先介绍了背景意义，问题提出和描述；其次对NBA30名球员的数据进行了Spss因子分析；最后，对模型与实际之间做出了贴合度解释，分析了球员篮球成绩的影响因素。

因子分析；计量模型；影响因素；篮球

美国职业男子篮球联赛（NBA，全称 National Basketball Association）是最受广大群体喜爱的篮球联赛之一，其日益精进的球员技能与球场战术对篮球运动的进步起了巨大的推动作用，因此对于NBA球员的数据分析很有意义[1]。

因子分析是指从研究相关矩阵内部的依赖关系出发，根据相关性大小把原始变量分组，使组内的变量之间相关性较高，而不同组变量的相关性则较低,把一些具有错综复杂关系的变量归结为少数几个综合因子的一种多变量统计分析方法[2]。在研究NBA球员数据时，由于指标较多增加了分析问题的复杂性和难度，因此用因子分析法找到合理的个数较少的指标去替代众多的指标[3]。

1 问题提出与描述

文中将会对抽取的30名球员在他们2010-2011年的各项指标的得分统计进行因子分析，来看这些指标间的相关性并进行指标分类，所有分析都采用了spss18程序。

本次数据来源于“搜狐NBA数据中心（2010—2011年）”，其中对原始变量进行了标准化：Z出场次数、Z场均时间、Z得分、Z二分命中（个数）、Z二分出手次数、Z二分命中率、Z三分命中（个数）、Z三分出手次数、Z三分命中率、Z罚球命中（个数）、Z罚球出手次数、Z罚球命中率。接下来的运行分析都是用对标准化后的变量进行的。

2 SPSS因子分析

2.1 模型建立

从搜集的数据中进行现实的逻辑推理，可以看出原始变量之间是有着不同的相关性的。例如，三分命中、三分出手次数和三分命中率之间应该是高度相关的。

在此，假设一个因子分析模型：

其中S代表因子总得分；λi代表第i个因子方差的百分比，(λ1＋λ2＋…λn)代表提取的n个因子累积百分比；Fi代表提取的第i个因子。

2.2 初步运算与结果分析

在输入自变量之前，经过分析，初步认为“Z得分”变量与其他变量不容易区分，也不好分类解释，因此在输入时将其提前剔除。

进行KMO和Bartlett的检验，KMO的度量值为0.625大于0.5；Sig.的值为0.00远小于0.05，说明这些变量可作因子分析。

公因子方差分析中的各个变量的因子共同度都在0.7之上，说明这11个变量很好的被3个因子解释。在解释的总方差中，第一个因子的特征值为5.061，大约占去方差的46.006%，基于过程内定取特征值大于1的原则，提取了前3个因子，这3个因子的特征值共占去方差的83.615%，所以提取的因子是合理的，并且放弃的其他9个因子解释的方差占不到20%，因此，能够说明前3个因子提供了原始数据的足够信息。在得出的碎石图中，前3个因子的特征根都大于1，从第4个主成分开始特征根就比较低，可以认为前3个因子能概括绝大部分信息。

在做出初始因子负荷矩阵后，发现前3个因子在原始变量上的载荷值相差不太大，故不能很明确的解释各个公因子，因此需要下一步的因子旋转。在得出的旋转后的因子负荷矩阵中，因子系数已经明显的出现分化。其中成分1中绝对值大的主要有：Z三分命中、Z三分出手次数、Z三分命中率、Z二分命中率、Z罚球命中率；成分2中：Z场均时间、Z二分命中、Z二分出手次数、Z罚球命中、Z罚球出手次数；成分3中：Z出场次数。

对以上的分类进行解释时，发现成分3和成分2是有现实意义的，但是，在成分1中，发现Z二分命中率是呈负相关，与实际意义有偏颇；而Z罚球命中率在成分2中会更好解释。基于此，下面会剔除这两个变量（Z二分命中率、Z罚球命中率）进行第二次的因子分析。

从旋转后的因子散点图中可以看出成分1、成分2和成分3与11个原始变量之间的关系。并且在成分得分协方差矩阵中，旋转后的成分1、成分2和成分3之间的相关系数为0，说明各因子间是互补相关的，提取的3个因子是合理的。

2.3 修正后运算和分析

基于第一次的运算和分析，尤其是对初始因子负荷矩阵和旋转后的因子负荷矩阵的分析，在这次的修正中决定剔除变量“Z二分命中率”“Z罚球命中率”。

表1 KMO和Bartlett的检验Tab.1 KMO and Bartlett’s test

从表1中可以得知，KMO度量值为0.665大于0.5，球形检验的Sig.值为0.00远小于0.05，检验P值十分接近于0,这就说明变量之间有很强的相关关系[4]。因此说明可以进行因子分析。

表2 公因子方差Tab.2 Common factor variance

从表2中可以看出这9个变量的因子共同度均在0.7以上，可以很好的被3个因子解释。

表3显示：根据内定取特征值大于1的原则，提取了前3个因子。第一个因子的特征值为4.511，大约占去方差的50.118%，前3个因子共占去方差的87.416%，比第一次高，所以提取的因子是合理的，放弃的其余6个因子解释的方差不到20%，更加说明前3个因子提供了原始数据的足够多的信息。

表3 解释的总方差Tab.3 Total variance explained

从图1中可知，前3个因子的特征根都大于1，从第4个成分开始特征根就比较低，且特征值小于1，因此前3个因子能概括绝大部分信息。

表4是初始因子负荷矩阵，可以看出这3个成分在变量上的载荷值都相差不大，因此需要进一步进行因子旋转以便更好的解释。

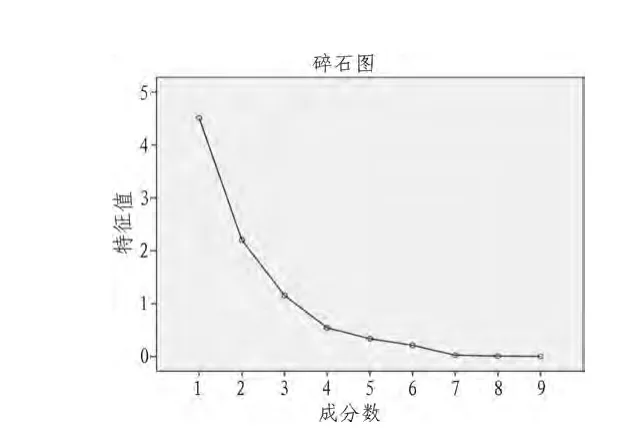
图1 碎石图Fig.1 Scree piot

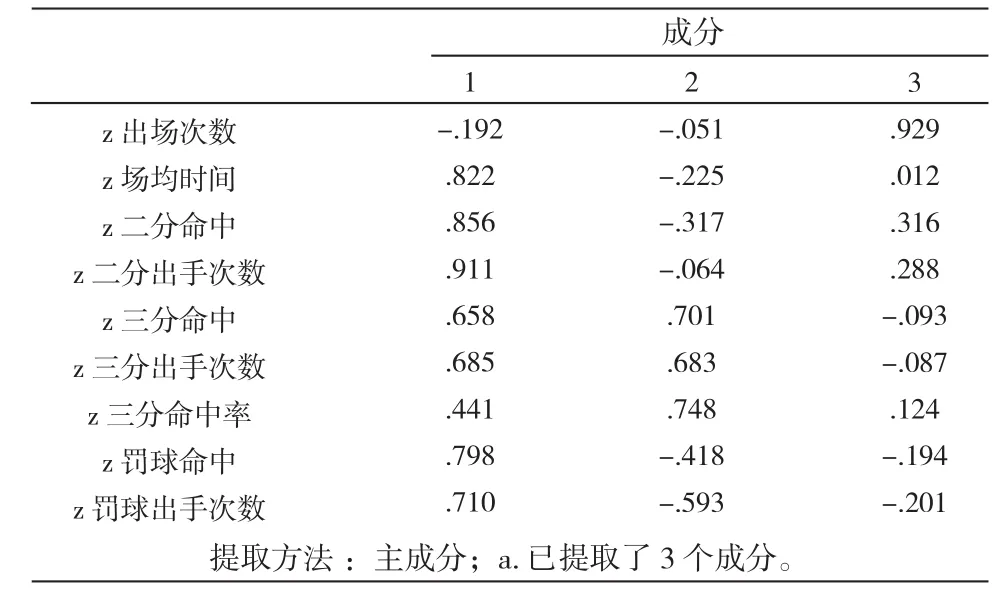
表4 成分矩阵Tab.4 Component matrix

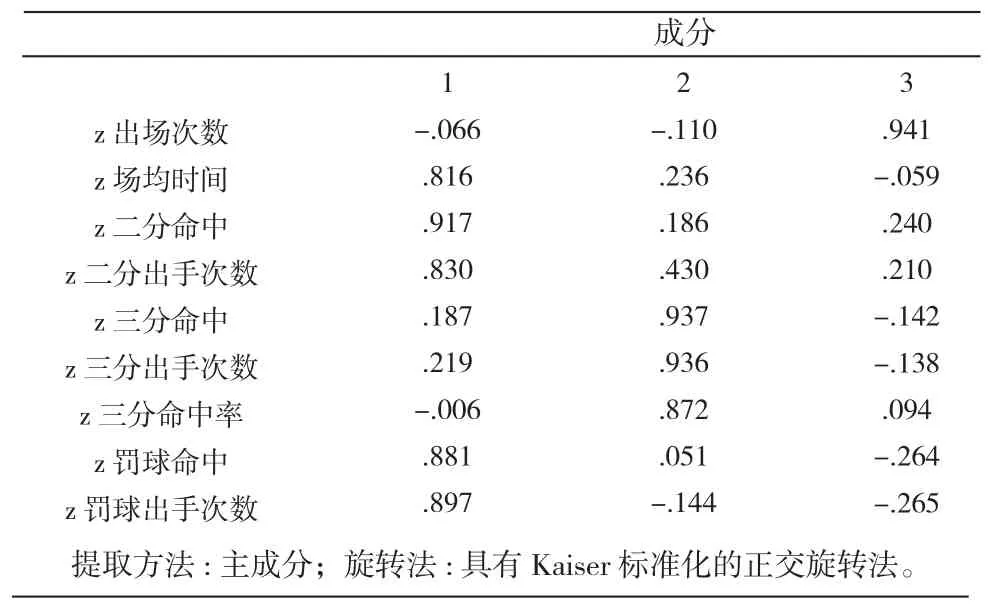
表5 旋转成分矩阵Tab.5 Rotating component matrix

从表5中得出，属于成分1的变量有：Z场均时间、Z二分命中（个数）、Z二分出手次数、Z罚球命中（个数）、Z罚球出手次数；属于成分2的变量有：Z三分命中（个数）、Z三分出手次数、Z三分命中率；属于成分3的变量有：Z出场次数。

可以看出，经过这次的修正而得出因子分类更加具有实际理论意义，并且解释也会更符合实际。

图2为因子散点图，可以形象看出成分1、2、3与9个变量之间的关系，此图中的各个变量能比较明显的划分出3类。

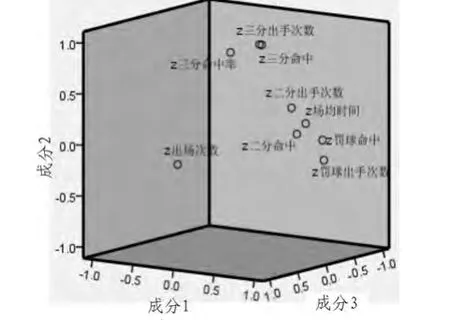
图2 旋转空间中的成分图Fig.2 Rotating components in space

表6中可以看出旋转后的成分1、成分2和成分3之间的相关系数为0，很明显各个因子互不相关，说明提取的3个因子是合理的、科学的。

基于本次修正的运算和分析，可以看到本次的因子分析不论是在指标数值上，还是实际意义上都是较好的，接下来，便是对得出的结论进行实际意义的解释。

3 模型总结

根据表9解释的总方差，将得出的数值代入在第一节中建立的模型：

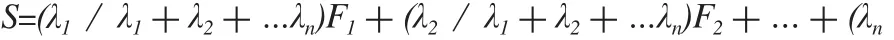
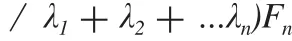
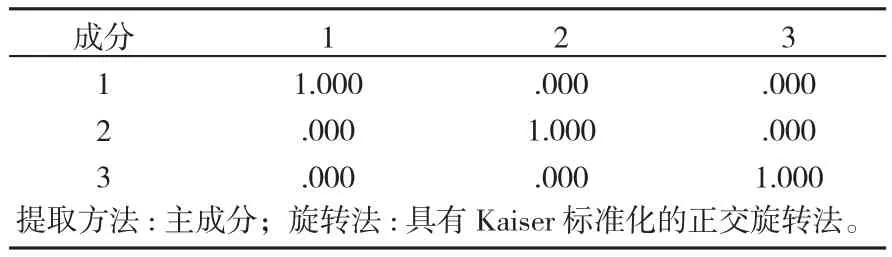
表6 成分得分协防差矩阵Tab.6 Ingredients of the covariance matrix

可以得出最终结果是：

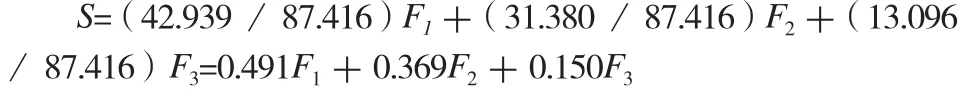
其中F1即为成分1，包含变量：Z场均时间、Z二分命中（个数）、Z二分出手次数、Z罚球命中（个数）、Z罚球出手次数；F2即为成分2，包含变量：Z三分命中（个数）、Z三分出手次数、Z三分命中率；F3即为成分3，包含变量：Z出场次数。

4 结 论

结合整个分析，对3个成分的实际意义解释如下：成分1为内线能力，内线的水平是一个球员得分的关键，篮下进攻成为最有效的得分手段[5]，因此它的系数0.491也是最大的；成分2为外线能力，外线能力在球场上是仅次于内线能力的得分因素，三分命中率是影响球队成绩的一项重要技术指标[6]，因此，其系数0.369也是仅次于成分1的系数；成分3为出场机会，显然，一个球员的内外线水平再高也得在能有上场的前提下才能展现。

因此，在得出了实际解释之后，可以将其借鉴应用于篮球的比赛战略上，在球场上最关键的是要捉住内线进攻，这是得分的核心所在，其次是外线的三分球得分，同时要合理分配优秀球员的出场时间和次数。

[1]方博.基于NBA球员的聚类分析和因子分析[J].科技视界,2013(11):80-82.

FANG Bo.Cluster analysis and factor analysis based on NBA player[J].Science & Technology View,2013(11):80-82.

[2]贾俊平.统计学[M].北京：中国人民大学出版社，2011.

[3]彭大松,左从现.因子分析的统计思想及在体育科研中的应用[J].四川体育科学,2007(3):18-20,23.

PENG Da-song,ZUO Cong-xian.The thought of factor analysis and the applying in sports[J].Sichuan Sports Science,2007(3):18-20,23.

[4]于浩飞.因子分析、多元回归分析与训练管理体系的建立[C]//中国体育科学学会运动训练学分会,中国体育科学学会运动训练学分会第六届全国田径运动发展研究成果交流会论文集，2013:1342-1353.

[5]江巍,孙庆祝,易洪刚.因子分析、聚类分析对第28届奥运会男子篮球比赛的应用研究[J].中国体育科技,2007（3）:94-97.

JIANG Wei,SUN Qing-zhu,YI Hong-gang.Factor and cluster analysis on the applied research of man.s basketball match in the 28th olympics games[J].China Sport Science and Technology,2007(3):94-97.

[6]刘毅.因子分析法对第16届女子篮球世锦赛各球队技术指标的分析[J].体育科技文献通报,2012(3):40-41.

LIU Yi.Factor analysis on technical indexes of each Team in the 16th women's basketball championship[J].Bulletin of Sport Science& Technology,2012(3):40-41.

The analysis of inf l uencing factors of the NBA basketball scores based on the measurement model

HUANG Xiao-min
（Tianjin University,Tianjin 300072, China）

NBA basketball league is very popular with the general population, and has an important influence for the basketball sports , therefore ,it is very meaningful for analysing the data of NBA players.This paper firstly introduces the background,and proposes and describes the problem.Secondly,using Spss factor analysis for the 30 players’ data of NBA .Finally, giving a rational explaination between the model and the practice, and analyses the influence factors of basketball players’ scores.

factor analysis;measurement model;influence factor;basketball

TN802

A

1674-6236(2014)14-0031-03

2013-09-27 稿件编号：201309210

黄晓敏（1988—），女，山东淄博人，硕士研究生。研究方向：创意经济，计量经济等。