一种新型的FPGA配置位流压缩算法

王 驰，王 健，杨 萌，来金梅

(复旦大学专用集成电路与系统国家重点实验室，上海201203)

现场可编程门列阵(Field Programmable Gate Array，FPGA)是由可编程功能块(Configurable Logic Block，CLB)、可编程互联单元以及可编程输入输出单元组成的模块阵列.为了满足应用电路日益复杂的资源和性能需求，FPGA的CLB阵列规模不断扩大，并越来越多地使用具有某些特定功能的可编程知识产权(Intellectual Property，IP)核来取代CLB实现.在这样的发展趋势下，FPGA中的静态随机存储单元(Static Random Access Memory，SRAM)以及配置位流中需要承载的配置信息随之增多［1］，由此人们提出了位流压缩的概念，即先对原有位流文件进行无损压缩后存储，下载时再由解压缩电路还原后传送给编程下载模块.压缩FPGA的配置位流能够有效减少其存储空间和下载时间，这在芯片规模和密度日益增大的今天变得更加具有研究和应用价值.在一些对存储器要求较为苛刻的环境下，例如航空电子领域，较小存储需求意味着更低的存储器成本和更强的鲁棒性.同时，位流压缩还能减少FPGA配置时间.由于从存储器中读取位流数据的速度相对较慢，而解压缩过程使用硬件实现，速度很快，因此位流的传输时间才是构成配置性能的瓶颈.压缩后的位流数据量减少，意味着位流文件的传输时间减少，从而减少了整体的配置时间.

目前所提出的位流压缩算法均基于已有的文本压缩算法.Huffman编码［2］以及算术编码［3］是基于统计模型的压缩方法，根据符号出现的统计频率生成编码树，在解压缩时除了需要传输压缩后的位流外还应提供编码树信息.LZ77/LZSS压缩算法［4］以滑动窗口数据作为待压缩数据的字典，将待压缩数据编码成字典窗口位置、长度表示的码字.因为LZ77/LZSS能够获得可观的压缩比，且解压缩硬件实现也不复杂，所以被公认为具有实用价值的算法.例如Xilinx的System ACE MPM配置解决方案已采用LZ77算法，并在配置电路中嵌入了相应的解压缩模块［5］.文献［6］针对Virtex-4(V4)FPGA位流［7］，对Huffman编码、算术编码以及LZSS的压缩效率做了一些比较.也有人尝试将多种算法结合以提高压缩效率，例如文献［8］尝试将LZSS与Run-length编码相结合，文献［9］尝试将LZ与Golomb编码相结合.

和普通文本不同，由于阵列的重复特性，位流的排布也会呈现一些规律性，若加以利用可以有效改善原有压缩效率.文献［8］和［10］均以帧为位流的划分单位，分析了帧与帧之间的相似程度，由此发现相似帧摆放在一起可以改善位流的压缩效率，从而提出了各自的帧重排算法.文献［11］同样利用了位流规律性，采用了BMC+RLE算法，在字典匹配时使用合适的掩码，从而增加了压缩时的统计字典的匹配命中率.文献［12］发现位流中约95%的数据为0，因此采用RLE编码对重复0数据进行具有针对性的压缩.压缩比(Compression Ratio，CR)为压缩后位流大小占原始位流大小的百分比，是衡量压缩算法的主要指标之一，然而具体采用何种压缩算法还应当充分考虑解压缩复杂程度和的硬件消耗.

本文对V4系列FPGA位流中存在的局部稀疏特性做了一些分析，并在此基础上提出一种新型压缩算法——符号维度压缩算法(Symbol Dimension Compression，SDC)，对出现频次较高的少1符号进行压缩编码，并对SDC压缩效率做了相应的数学分析.SDC的解码算法十分简单，易于硬件实现.并通过实验分析了符号长度、压缩阈值以及资源利用率对本文算法CR的影响，发现符号长度及压缩阈值合适的选值能够获得较为理想的结果.同时本文还与另外一种实用的位流压缩算法LZSS算法进行了比较，发现压缩效率普遍提高了8%～12%.

1 维度压缩算法

1.1 位流特征

虽然FPGA中的可配置资源理论上能够工作在2n(n为控制该资源的SRAM个数)个状态，但其实际工作状态只会有一种，因此配置必然具有一定的局部性，体现在两方面:(1)需要配置的单元的分布存在局部性.以CLB的一个逻辑片(slice)为例，虽然能够实现多种功能，如5输入以内任意组合或时序逻辑、16比特或32比特随机存储器(Random Access Memory，RAM)或移位寄存器、移位链逻辑等，但实际工作时大部分情况下只会用到这其中的某一项功能，其他可配置单元处于“闲置”状态.(2)同一配置单元相关SRAM的配置也存在局部性.如一个8选1的多路选择器(Multiplexer，MUX)可能的MOS结构如图1所示，该MUX的选通路径由10个SRAM控制.假设默认上电时SRAM的初始值使得所有MOS管均处在关断状态，当需要选通一个路径时，只需要翻转两个SRAM值便能使其导通，也就是说只有少数SRAM需要重新确定配置值，而其他SRAM处在上电默认状态即可.

实际上，FPGA可以看成是以MUX为基本可配置单元构成的复杂可配置电路.例如，配置逻辑片中4输入查找表(Look-Up Table，LUT)本质上就是一个16选1的MUX，而其他互联路径或数据路径的选择同样是以MUX来实现.FPGA位流由0、1比特组成，其中配置部分的每一个比特对应FPGA中的一个SRAM，因此SRAM翻转分布的局部性特征必然会反映到位流中.

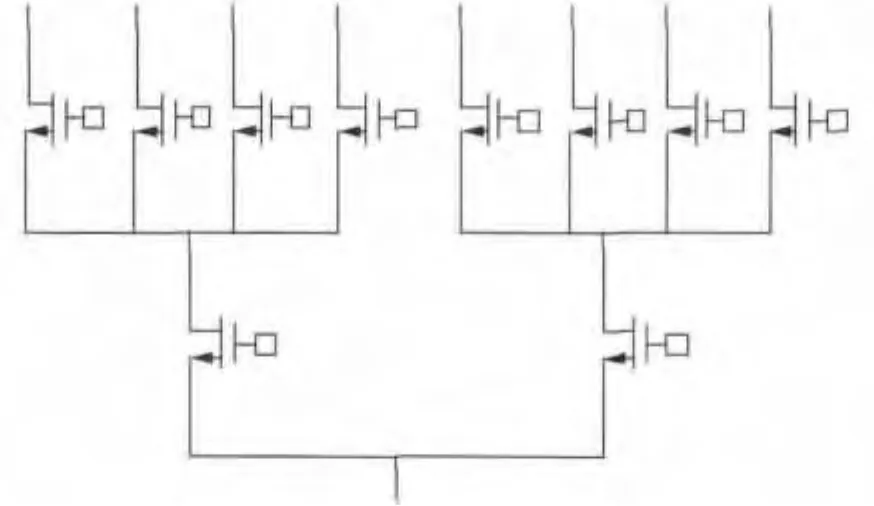
图1 8选1 MUX MOS级电路结构图Fig.1 MOS-level schematic of 8 to 1 MUX

Xilinx公司V4作为典型的现代商用FPGA芯片，其电路结构具有相当的代表性.因此，本文选用V4系列FPGA的位流作为实验对象.即使资源利用率使用达到94%，V4位流中需要由默认值翻转的SRAM数量也不到总数的7%，如图2所示.

从图2中还可以看出，SRAM翻转率和资源利用率呈现一定的正相关性.资源利用率越高，需要配置的SRAM也就越多.

为了验证位流中存在的局部性，对V4若干位流进行了统计分析，发现了一些共性，这里以rsdecode位流为例.我们先对原二进制位流按照一定的比特长度进行打包后转换成符号流，这里我们分别选取符号长度Ls分别为8，16，24.V4位流以0为默认值，我们将符号中含1的个数称为符号的维度Ds.通过分析这些符号出现的频率，我们得到图3的统计结果，并发现:

(1)符号Ds越高，出现频率往往越小;

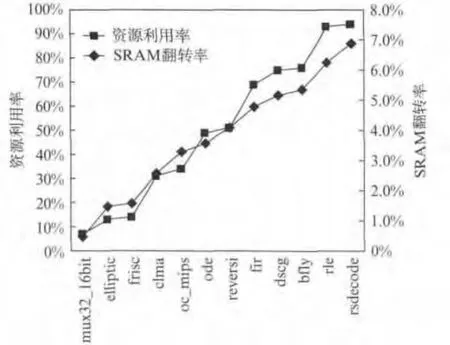
图2 资源利用率和SRAM翻转率的关系图Fig.2 Relationship between resource utilization and SRAM overturn ratio

(2)0维符号的出现频率远大于其他维度符号;

(3)当Ds大于某值之后，符号的出现频率不再显著，如Ls=8，当Ds＞2后符号出现频率接近于0;

(4)Ds越大，0维符号的出现频率会越小.

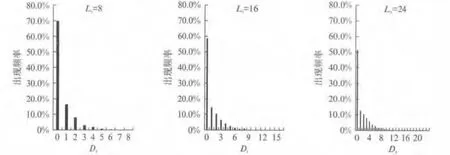
图3 不同维度符号的频率分布Fig.3 Frequency distribution of symbols with different dimensions

上面的发现表明，在位流中确实存在很明显的局部稀疏性质，并且少1符号出现的频次占符号总数较大比重，这为之后的符号维度压缩算法提供了实际的统计依据.

1.2 编码方法

Huffman编码已经被证明为最优的压缩编码方法［2］，但若要将其应用到位流压缩中，不仅需要大量统计符号频率，解压缩时解压缩电路还需要解析Huffman树，因此实现复杂度较高，且解析过程需要多个时钟周期，制约解压缩电路的性能.本文借鉴了Huffman的编码思想，即使用较少的比特来表示出现频次较高的符号.但和Huffman编码不同的是，根据上一节中分析得出的局部性结论，我们先将符号按维度划分后再用单进编码方法(Unary Coding)对这些类别进行前缀编码，其编码树如图4所示.单进编码为霍夫曼编码的一种特殊情况，当元素概率分布呈现为P(n)=2－n时其压缩效率达到最优.图3中已经呈现出符号频率分布一定的指数趋势，且单进编码的编码树结构固定，可直接固化在解压缩电路中，故本文加以采用.

图4 采用单进编码的前缀编码树Fig.4 Prefix encoding tree using unary coding

图4中，S(n)={s|s∈A，D(s)=n}，其中A为符号全集，D(s)为符号s的维度.我们可以从比特值为1的位置出发对原码进行编码.为了分析方便，我们暂时取符号长度为8，表1为具体编码方式.S(0)不需要进行额外编码.S(1)的1可能存在于8个位置上，因此需要3比特来对位置进行编码.S(2)有两个1，因此1的位置是一个二维坐标，同理对于n≥1的S(n)，都可以表示为n维向量，这也是为什么称1的个数为维度的原因.S(2)可以表示成图5那样的二维矩阵，其中行号为第一个出现的1的位置，列号为第2个出现的1的位置，划斜杠的方格表示不可能存在的情况.在这种情况下，S(1)有28种可能，因此需要用5比特来进行编码.其具体编码已经按照一定顺序标注在图5的方框中.我们可以推导出，位置编号p可以直接表示为

表1 压缩编码示意Tab.1 Example of compression encoding

其中，r为行号，c为列号，Ls为符号长度.

解码时，同样可以通过p以及图5提供的查找表迅速还原成原码，可以直接通过简单的组合逻辑来实现，和LZSS的解码电路［13］相比更加简单.

对于更高维度的符号，同样可以利用1位置组成的向量进行编码.更一般地，n维符号(n≥1)编码方法可以表示为如下伪代码:

图5 2维符号编码示意图Fig.5 Encoding of 2-D symbol

其中，Alphabet(1)为长度为1的符号全集，且按照字符串升序，同时也是二进制升序排列.返回的encode_table中各符号元素的编码值即为该元素的下标.

研究发现，当符号维度大于某个值时，压缩效率不再明显改善，因为符号出现频次较低，且编码CR不高，因此没有必要对维度超过该值的符号进行编码.我们将停止编码的起始维度称为维度编码的压缩阈值，在实验结果中我们会给出T对CR造成的影响.

1.3 压缩效率

维度压缩算法本质上是一种熵编码.其熵值可以表示为

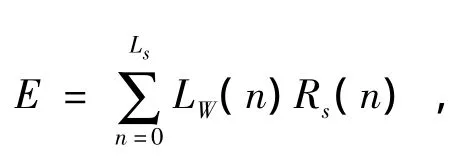
其中，Ls为符号的原码长度，n为维度，LW(n)为符号压缩码长度，即前缀码和编码长度之和，Rs(n)为符号出现的频率.假设T为编码阈值，那么

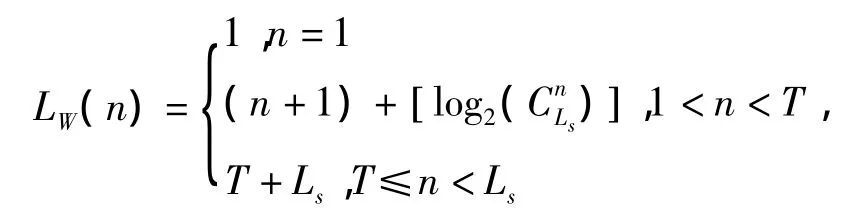
因此，CR可以表示为CR=E/Ls.可见，对于同一个位流来说，T和Ls的选择会对CR产生影响，并且CR的值不小于1/Ls.

2 结果

实验在VS2010开发环境下采用C++编写主要压缩算法.所用测试用例均来源于opencores等开源网站.

2.1 符号长度

研究发现，Ls的选取既不能过小，也不能过大.Ls过小，前缀码加上压缩编码的长度很容易就超过Ls，起不到压缩的作用.Ls过大，Ps(0)会相应减小，从而反作用于CR.因此需要通过实验数据来选取一个较优解.本文选取不同的Ls对测试用例的位流进行压缩，图6给出了其中6个不同资源利用率的结果.可以看出，在Ls=22时，rsdecode的CR为32.2%，在所有不同Ls对应的所有CR值中最小，其余例子也都在Ls=22时呈现最低CR.因此，对于V4位流来说，当Ls为22时整体压缩效率最理想.

图6 符号长度的选取对CR的影响Fig.6 Symbol length's effect on CR

2.2 压缩阈值

符号的维度越高，表示一个符号的坐标需要信息也就越多，因而会使得它的压缩编码的效率变低.同时，由于维度高的符号出现频率较低，因此高维度符号的压缩对整体压缩的贡献并不大.我们在Ls分别为12，16，20时选用不同压缩阈值对测试用例进行压缩，得到图7.可以看到当T大于某个值时，所有例子的压缩效率已经不再随T的增大而有明显改善.如Ls=12，T＞2后压缩效率没有明显变化.

图7 压缩阈值T对CR的影响Fig.7 Compression threshold's effect on CR

2.3 和LZSS比较

LZSS算法因具有可观的压缩比和简单的解压缩过程，被公认为是具有实用价值的压缩算法［11］.将SDC算法和LZSS算法的压缩效率进行了比较，得到图8的结果，可以看出，在rsdecode例子中SDC算法的CR比LZSS低8%，而其他例子的CR均低于LZSS算法CR 12%左右.不同资源利用率的位流文件大小是相同的，因此，资源利用率越低位流中的冗余信息就越多.SDC算法能够有效抑制这些冗余信息，从图8中还可以看出随着资源利用率降低SDC压缩效率也在逐步提高.这是因为在资源利用率不高的情况下SRAM翻转率变低，因而Ps(0)会相应增大，更有利于压缩.

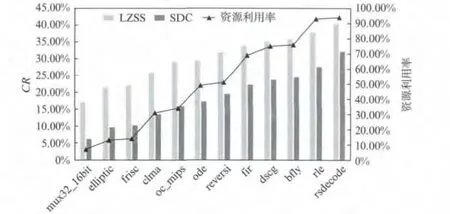
图8 SDC和LZSS压缩效率的比较Fig.8 CR comparison between SDC and LZSS

3 结论

通过对V4 FPGA若干位流的统计分析，首次发现了其中存在的局部稀疏特性，并由此提出了一套新型的压缩方法，根据符号中1的个数对符号进行分类和编码，为位流压缩提供了一种全新的思路.本文分别对符号长度、压缩阈值以及资源利用率对SDC压缩效率可能产生的影响进行了实验分析及论证，得出如下结论:(1)符号长度太大太小压缩效率均不理想，其值可以通过统计分析来进行选取;(2)当压缩阈T值大于某值时，压缩效率不再随着T的增大得到明显改善，因此可以仅对维度在以内的符号进行编码;(3)SDC能够有效抑制低资源利用率时产生的冗余信息.此外，本文算法相应的解压缩算法比较简单，易于硬件实现.

［1］Sellers B，Heiner J，Wirthlin M，et al.Bitstream compression through frame removal and partial reconfiguration［C］∥Field Programmable Logic and Applications.Prague，Czech Republic:IEEE Press，2009:476-480.

［2］Huffman D A.A method for the construction of minimum redundancy codes［J］.Proc IRE，1952，40(9):1098-1101.

［3］Witten I H，Neal R M，Cleary JG.Arithmetic Coding for Data Compression［J］.Communications of the ACM，1987，30:520-540.

［4］Ziv J，Lempel A.A universal algorithm for sequential data compression［J］.IEEE Transactions on Information Theory，1977，23(3):337-343.

［5］Xilinx Corporation.Xilinx FPGA Configuration Data Compression and Decompression［EB/OL］.(2003-01-01)［2014-01-01］.http:∥www.cs.york.ac.uk/rts/docs/Xilinx-datasource-2003-q1/whitepapers/wp152.pdf.

［6］Li Z，Hauck S.Configuration Compression for Virtex FPGAs［C］∥Field-Programmable Custom Computing Machines.California，USA:IEEE，2001:147-159.

［7］Xilinx Corporation.Virtex-4 FPGA Configuration User Guide［EB/OL］.(2008-04-01)［2014-01-01］.http:∥www.xilinx.com/support/documentation/user_guides/ug070.pdf.

［8］Hauck S，Wilson W D.Runlength compression techniques for FPGA configurations［C］∥Field-Programmable Custom Computing Machines.California，USA:IEEE，1999:286-287.

［9］Mao J，Zhou H，Ye H，et al.FPGA bitstream compression and decompression using LZ and golomb coding［C］∥Proceedings of the ACM/SIGDA international symposium on Field programmable gate arrays.California，USA:IEEE Press，2013:265-265.

［10］Pan J H，Mitra T，Wong W F.Configuration bitstream compression for dynamically reconfigurable FPGAs［C］∥International Conference on Computer-Aided Design.California，USA:IEEE Press，2004:766-773.

［11］Qin X，Muthry C，Mishra P.Decoding-Aware Compression of FPGA Bitstreams［J］.IEEE Transactions on Very Large Scale Integration Systems，2011，19(3):411-419.

［12］Jia R，Wang F，Chen R.JTAG-based bitstream compression for FPGA configuration［C］∥Solid-State and Integrated Circuit Technology.Xi'an，China:IEEE，2012:1-3.

［13］Huebner M，Ullmann M，Weissel F，et al.Real-time configuration code decompression for dynamic FPGA selfreconfiguration［C］∥Parallel and Distributed Processing Symposium.New Mexico，USA:IEEE，2004:26-30.