基于自适应增强的静态随机存储单元失效率快速仿真算法

韦 峰，朱恒亮，曾 璇

(复旦大学专用集成电路与系统国家重点实验室，上海201203)

当前集成电路制造工艺已经进入纳米时代，随着工艺特征尺寸的进一步减小，随机工艺偏差对器件可靠性的影响不容忽视.静态随机存储器(Static Random Access Memory，SRAM)作为非挥发性存储器中的一员，具有高速度、低功耗等优点，在片上系统中占据主导地位，考虑到容量和功耗问题，SRAM一般采用最先进的制造工艺［1］.SRAM电路由数以亿计的重复的位单元结构构成，为了让整块存储器芯片正常工作，需要保证每个位单元都正常工作.所以，单个SRAM单元的可靠性对整个存储芯片的性能至关重要.其中，随机工艺偏差对SRAM单元的影响最大，它会严重恶化晶体管的关键性能参数，如阈值电压Vth，导致失效率迅速增大.因此，深亚微米效应是降低存储芯片不良率的重要因素，在芯片设计中，对电路性能的鲁棒性分析建模有非常重要的意义.

近年来，一系列基于统计分析的方法被用于探索SRAM单元电路的验证和相关的电路失效概率这一极端概率事件(Probability of Extreme Events)［2-6］.最传统的方法是基于蒙特卡洛采样(Monte Carlo，MC)的分析方法［3-4］，或者建立SRAM单元的性能分析模型来预测SRAM单元电路的失效率［2，5］，甚至两种方法的结合［6］.由于SRAM单元电路失效概率是一个极端概率事件，失效区域无法直接获得，简单的蒙特卡洛实现需要大量的采样点来捕捉足够准确的信息.分析模型的不足之处在于精度以及模型对电路行为的刻画能力.因此，绝大多数传统方法无法快速准确地估计像SRAM单元电路失效这类极端概率事件.文献［7］提出了旨在改进蒙特卡洛采样效率的重要性采样(Importance Sampling，IS)方法.在重要性采样中，原始的概率密度函数(Probability Density Function，PDF)会向SRAM单元的极端失效区域偏移.该偏移后的分布更接近失效区域的实际分布情况，所以失效区域可以被更加有效地采样.因此，在重要性采样中，最优偏移量是决定因素，该偏移量直接决定了重要性采样的实际分布函数，并对快速预测和精度有直接影响.文献［3-4］中，IS方法的实际最优分布参数是通过最小化二范数的方法来获得，它的变种椭球采样则适用于高维问题.文献［8］结合了数据挖掘和极值理论来过滤一些无效的采样点，这种方法屏蔽了一些不在目标失效区域中的采样点.该方法首先采用MC方法或IS方法进行初始化采样，通过样本学习，选取一个有合适阈值和安全边界的支持向量机(Support Vector Machine，SVM)实现分类器;然后，用MC方法生成足够多的采样点，分类器对处于分布函数97%的尾部采样点进行筛选，最后对未被分类器过滤的采样点进行仿真，达到加速目的.

以上介绍的基于MC方法的采样算法需要进行大量的仿真计算，为了覆盖完整的失效区域(使SRAM单元电路失效的相关参数构成的区间)，这类方法会产生大量无效采样点(失效区域外的采样点)，极大了影响了采样算法的收敛性.本文针对SRAM单元电路失效率仿真的精确估计这一问题进行深入研究，借鉴了统计学习领域的相关知识，并与改进的高效IS算法相结合，提出了基于自适应增强(Adaptive Boosting，AdaBoost)学习分类的SRAM单元失效率仿真算法.AdaBoost分类学习是本文算法的核心，它广泛应用于模式识别领域，本文将其应用在极端概率估计事件中，该方法利用学习算法将大量弱分类器组合构建出一个强分类器，对错分类样本敏感，适合于偏置样本分类，分类器可以精确检测出不必要的采样点.该方法与基于SVM学习的方法相比，具有更易于实现、参数依赖性低、分类效果更优等优点.本文还提出了基于最小交叉熵(Minimum Cross-Entropy，MCE)的改进的IS算法，迭代的优化分布函数的参数，不断优化的分布参数能使采样过程更快接近实际最优分布，收敛速度更快，大大降低了仿真时间.

1 问题定义

1.1 6-T单元结构及工作原理

SRAM单元结构晶体管级电路如图1所示，它由6个管子组成，整个单元具有对称性.M1～M4构成双稳态电路，用来锁存一位数字信号，M5、M6是传递晶体管，它们在对存储器进行读写操作时起到将存储单元与外围电路进行连接或断开的作用.

1.2 读写稳定性失效概率分析

对单元存取都需要先将字线(Word Line，WL)置为高电平.读操作时，WL为高电平时传递晶体管导通，使存储单元的信息传递到位线(Bit Line，BL)，单元信息的反信号传递到位线BLB(BL的反信号)，外围电路通过BL和BLB读取信息;写操作时，SRAM单元阵列的外围电路将电压传递到BL和BLB上作为输入，WL使能后，信息写入存储单元［2］.一般SRAM单元的读操作最容易出现失效情况，而6-T单元一次典型的读操作包含对位线的预充电以及通过传递晶体管读取位信息两个操作.当传递晶体管被打开时，其中一根位线通过传递晶体管和反相器下拉晶体管放电，BL和BLB间的电压差经过敏感放大器放大后输出，读失效定义为读取单元信息时间超过临界时间.

图1 SRAM单元电路结构Fig.1 SRAM cell structure

2 研究背景

2.1 MC 方法

实际SRAM单元电路中的一些工艺偏差参数可以用一组独立随机变量ξi(i=1，2，…，m)表示，比如晶体管的阈值电压和有效沟道长度.给定它的PDF为f(ξi).由于变量ξi的独立性，它的联合PDF可以表示为:

第 j个蒙特卡洛采样点 ξj=，…)由每个独立随机变量分布联合构成.

假设F(ξ)表示与工艺参数ξ相关的电路性能指标，例如SRAM单元的静态噪声容限，读写时间边界.该指标需要通过专业仿真软件如HSPICE对电路进行晶体管级的仿真获得，由于采样点数目巨大，仿真过程十分耗时.令F0为该性能指标的阈值，当出现F(ξ)＜F0时，电路定义为失效，是一个极端概率事件.我们定义一个指示函数来描述电路的工作情况:

因此，利用公式(2)，SRAM单元电路的失效概率可以表示为如下形式［5］:

PMC表示采用MC方法获得的失效概率估计，一般来说，f(ξ)是给定的，可以通过实际测量得到，而指示函数I(ξ)是未知的，不能直接得到，需要对电路进行晶体管级精确仿真.MC方法需要对整个失效区域进行采样，得到该区域中所有采样点的指示函数I(ξ)，MC采样方法理论上需要的采样点数目将会在2.3节中给出分析.

2.2 IS 方法

虽然MC方法是一个可靠的方法并且被各领域作为一种标准仿真方法广泛应用，该方法仍具有一些致命缺陷.MC方法的缺点就是收敛速度过慢，不适用于处理SRAM电路失效概率估计这类极端概率事件.如图2所示，为了方便可视化，以二维参数为例，SRAM电路失效区域用红色标出，采用MC方法采样，给定中心点的分布进行采样，虚线表示采样半径.由于SRAM单元电路失效是典型的极端概率事件，失效区域只占极小的比例，为了能够覆盖失效区域，MC方法需要庞大的采样点仿真计算.因此，文献［3］提出了重要性采样方法，将采样中心偏移到失效区域，该方法能在极小的精度损失情况下，极大地提高采样效率，是一种方差减少的快速采样方法.

重要性采样算法通过选取一个不同的概率密度分布g(ξ)替换原始的概率密度分布f(ξ).在新的概率密度分布g(ξ)下，大量的采样点集中我们更关心的失效区域内，此时，失效概率估计可以表示为:

其中，ω(ξ)为权重函数，代表新的分布函数下的采样点在原始分布下权重函数.理论上，重要性采样的最优分布只需要一个采样点即可以提供电路失效概率的精确估计.该最优分布形式如下:

然而，由于I(ξ)未知，并且PIS正是我们最终需要计算的概率估计，gideal(ξ)无法通过上式直接获得.因此，我们需要构造另一个概率密度分布来尽可能替代理想分布gideal(ξ).这可以通过最小交叉熵的方法构造近似最优概率密度分布h(ξ)来解决.

2.3 优值系数

对于基于MC方法的这一类采样算法，优值(Figure of Merit，FoM)是判定概率估计是否收敛的一个重要标准［4］.它的计算公式如下:

P是事件概率，VAR是概率估计P的方差.公式(7)和(8)给出了MC和IS的方差计算公式:

要获得90%精度(ε=0.1)和90%置信度(δ=0.1)，大概需要100/PMC数量级的采样点.如果SRAM单元电路的失效概率为1×10－5量级，MC方法至少需要107量级的采样点.

图2 失效区域分布Fig.2 The distribution of failure region

图3 SRAM失效概率估计算法框架Fig.3 The framework of failure rate estimation

3 基于AdaBoost分类的拟重要性采样算法

本节引入基于AdaBoost学习方法的SRAM单元电路失效概率仿真算法.整个仿真系统框架如图3所示，对于SRAM单元电路失效概率估计而言，关键是确定理想实际失效区域分布相对于原始分布的偏移量，为了寻找理想实际分布，本文提出了基于最小交叉熵的方法.同时，为了避免对大量无效采样点进行精确电路仿真，本文引入了AdaBoost学习方法对样本进行分类预测，筛选出失效区域中的采样点，大大节省了不必要的采样点仿真计算.

3.1 最小交叉熵方法

公式(5)已经给出了采用IS方法获得理想的分布函数gideal(ξ)，但由于指示函数I(ξ)未知，理想的偏移均值无法获得.本节通过最小交叉熵方法逼近最优偏移均值.该方法被广泛用于各种统计推断和机器学习问题中，MCE方法本质上是最小化一个分布与另一个分布的Kullback-Leibler距离，假设h(ξ)为理想分布gideal(ξ)实际近似分布，表示成数学公式［10］如下:

Egideal表示理想分布函数期望，为了使实际分布h(ξ)最接近最优分布gideal(ξ)，需要求公式(10)的最小值，文献［13］给出了最小化公式(10)的数值优化表达式:

对于SRAM单元电路失效概率估计事件，由于Eξ无法直接获取，需要通过采样计算，公式(11)属于数值优化问题，计算代价太大，所以MCE方法无法直接应用.用μ表示SRAM单元电路工艺参数的均值，σ表示其对应的方差，h(ξ)为高斯分布N(μ，σ)，ξ=［μ，σ］.结合公式(4)，代入公式(11)得到关于 SRAM 单元电路失效概率的最优分布参数公式:

公式(12)的数值优化问题可以通过分析方法解决，公式(12)的最优解可以通过MCE公式求导得到:

文献［13］运用公式(13)中第一个公式来获得最优分布的实际近似最优偏移量，但文献［13］仅进行了一次计算，实际运用中无法获得准确的近似最优分布参数.同时，文献［13］忽略了方差与偏移量的相关性，没有给出最优方差逼近的计算公式，本文推导的公式(13)充分结合了μ和σ的相互影响，同时结合3.3节中提出的收敛判定标准，更加准确地、系统地给出了最优分布的逼近方法.

3.2 AdaBoost分类器

AdaBoost算法是一种机器学习方法，由Freund和Schapore提出［9］.算法1描述了AdaBoost的工作原理，AdaBoost方法是一种迭代算法，在每一轮中加入一个新的弱分类器，直到达到某个预定的足够小的错误率.每一个训练样本都被赋予一个权重，表明它被某个分类器选入训练集的概率.如果某个样本已经被准确地分类，那么在构造下一个训练集中，它被选中的概率就降低;相反，如果某个样本点没有被准确地分类，那么它的权重就得到提高.通过这样的方式，AdaBoost方法能“聚焦于”那些较难分(更富信息)的样本上.

在具体实现上，最初令每个样本的权重都相等，对于第K次迭代操作，我们就根据这些权重来选取样本点，进而训练分类器Ck.然后根据这个分类器，来提高被错误分类的样本的权重，并降低被正确分类的样本的权重.然后，权重更新过的样本集被用于训练下一个分类器Ck+1.整个训练过程如此迭代进行下去［11］.

算法1:AdaBoost 分类学习算法

3.3 整体算法框架

重要性采样框架内最重要的环节是确定实际分布相对于原始分布的偏移量，构建偏向失效区域的新的最优实际分布，如图2所示，即搜索最优分布gideal(ξ)的一个近似分布.

3.3.1 初始化分布选取

采样仿真问题首先要决定引入多少个参量作为输入来对工艺偏差建模.对于SRAM单元电路模型，CMOS晶体管的工艺偏差参数主要是阈值电压Vth和有效沟道长度Leff.而在这些参数中，Vth占主导地位.实际运用中，Vth偏差模型被定义为典型的高斯随机变量.

选定参变量之后，需要确定一个初始化分布迭代的逼近重要性采样的最优分布.一个好的初始化分布能产生更多的电路失效采样点，加速失效概率估计算法的收敛.因此，本文提出了一种启发式方法可以使原始分布快速偏移到一个更容易产生失效事件的初始点.首先用MC方法均匀采样一些点(大概500～1 000)，保证样本空间可以被均匀覆盖.然后，对这些样本进行晶体管级的电路仿真，筛选出给定性能约束下的电路失效的样本.对筛选出的失效样本集合运用最小2-范数求解初始化偏移量lini:

li为失效区域样本点参量值，为失效区域样本集合的均值.公式(14)给出了初始化的中心点偏移量，使PDF更加接近失效区域的PDF.第二阶段需要结合公式(13)，数值迭代求解最优平均偏移量.

3.3.2 失效概率估计

公式(6)给出了FoM值的计算公式，一旦FoM值达到阈值，可以认为失效概率估计Pfail趋于收敛.不同于现有方法，本文在每一次迭代过程中利用公式(13)优化分布参数，降低FoM的值.IS方法的FoM值的数学表达式如下:

在没有任何数值约束条件下，FoM的最小值为0.因此，最直接的办法就是在每一次迭代中让公式(15)中的分子尽可能地接近0，加快仿真收敛速度.原问题转化为:

由于上述方差表达式中的第二项的倒数并不能保证非负，该方差表达式并不是一个凸规划问题.文献［12］指出，当且仅当公式(15)的第二项为非负时，上述可导函数为凸函数.计算公式(15)的导函数的极值点，得到的均值和方差的数学表达式同公式(13).

基于重要性采样的SRAM单元电路失效概率估计可以通过上述计算流程得到.在每一步的迭代中，近似分布估计的平均值和标准偏差都会变化，并逐渐向最优分布的平均值和标准方差逼近.但由于标准方差σ的计算严重依赖于平均值μ的计算，有可能导致算法没有收敛或者收敛于偏离全局最优的一个局部最优解.因此需要在初始化中，尽可能地选出接近失效区域的初始点.算法2给出了基于综合上述各种方法的SRAM单元失效概率估计算法的整体框架.

算法2:SRAM 单元电路失效概率分析算法

(续表)

4 结果

本文提出的SRAM单元电路失效概率估计算法采用C++/MATLAB混合编程实现，结合了HSPICE电路仿真工具和32 nm的PTM工艺预测模型.如图1所示，SRAM单元读操作受晶体管M3和M4的阈值电压变化影响最大，本文中算法实现针对Vth1和Vth2建模，亦可以扩展到高维情况，限于篇幅原因，本文不扩展探讨.SRAM单元中指定MOS管的阈值电压的原始分布如下:所有分布假设为标准正态分布，标准分布的均值为0.466 V.阈值电压的标准差为均值绝对值的10%，即0.046 6.电源电压Vdd=0.9 V.位线读取信息的敏感电压差为0.07 V，本实验中，SRAM单元的失效概率为6.67×10－4.

4.1 分类效果分析

本文提出的算法主要基于AdaBoost分类算法实现，该算法其实是一个简单的弱分类算法提升过程，这个过程通过不断地训练，可以提高对数据的分类能力.图4为AdaBoost分类器的训练过程，从图中可以看出，随着迭代次数的增加，分类效果越来越精确，样本分布逐渐接近实际失效区域分布.但是，SRAM单元电路失效事件是极端小概率事件，训练学习样本是偏置的.SRAM电路正常工作样本(反例)要远远多于电路失效样本(正例)，正例分类错误的代价相对较高，直接采用AdaBoost分类方法预测精度比较低.本文提出了针对非均衡问题调节分类器的方法，就是对分类器的训练数据进行改造.通过对反例样本进行欠抽样或者样例删除处理，选择那些离决策边界较远的样例进行删除，另一种数据处理方法就是基于代价函数来调整错误权重向量D.考虑到小类别中只允许更少的错误，可以基于代价函数来调整错误权重向量D.本文采用欠抽样方法，改进的AdaBoost分类效果如图5所示，初始样本集合大小为1.0×105.从图中可以看出，原始失效样本的数目极少，只有418个，对原始数据进行分类学习，再以原始样本集验证分类器性能，仍有1/3的点无法正确分类，而对处理后的学习样本进行学习，只有不到1/10的点被错误分类.处理前后分类精度从67%提高到90%.

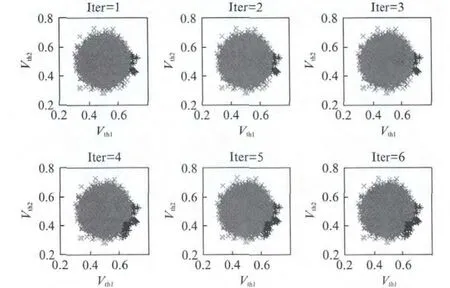
图4 AdaBoost分类器训练过程Fig.4 The training process of AdaBoost classifier

图5 学习样本集改进前后的错分率Fig.5 The miss hit rate of learning samples

文献［8］中提出了基于SVM分类学习的方法，SVM是当前最优秀的非线性分类器之一.表1比较了本文提出的AdaBoost分类方法与SVM分类器的性能对比.从表中可以看出，随着采样点个数的增加，AdaBoost方法预测准确度要比SVM高很多，稳定后SVM分类器的分类精度保持在75%，AdaBoost分类器的分类精度稳定在91%左右.为了保证实验公正性，两种方法采用相同的学习样本.

4.2 算法的收敛性分析和精度比较

如前所述，优值系数FoM是决定概率估计收敛与否的标准.试验中，我们设定FoM的阈值为0.1，即收敛后的概率估计值具有90%的精度和90%的可信度.SRAM单元读操作失效概率估计的各种方法的测试结果如图6所示.上图为传统的MC方法和IS方法概率估计，下图为序列重要性采样(SIS)，基于SVM分类学习的重要性采样(SVM-IS)以及基于AdaBoost分类学习方法的改进型重要性算法(Ada-QIS)的概率估计.这些方法最终的失效概率都非常接近，一般以MC方法收敛后的测量值作为标准值，因此本文的方法具有很高的精度.在实验中，MC方法需要106以上量级的采样点才能达到收敛，而SVM-IS方法及Ada-QIS方法的采样点数量级在103左右.除此之外，相比于其他方法，本文提出的方法迭代了很少次数就达到收敛，即基于交叉熵的IS方法能够迅速寻找到最优实际分布的最佳近似分布.另外，通过观察这一类IS算法，可以发现重要性采样对样本分布非常敏感，并直接影响到估计的精度和效率.实际采样中，很多采样点是在失效区域外的，SVM分类器和AdaBoost分类器的引入大大减少了由这些点导致的不必要的仿真计算.本文提出的基于AdaBoost分类的拟重要性采样算法，不仅通过分类器过滤了很多无用的采样点，同时迭代地降低样本方差，从两方面使采样算法收敛加速，因此其效果要比当前最先进的基于SVM分类过滤的算法要快1倍以上，而相比于标准的MC方法要快103的数量级，随着失效概率的降低，这种优势将更加明显.同时，由于SRAM单元电路最耗时间的部分就是对电路的精确仿真，因此，采样点的个数间接表示了该算法的运行时间.

表1 分类器性能比较Tab.1 The performance of the two classifiers

图6 SRAM单元电路失效概率估计算法比较Fig.6 Comparison of multiple algorithms for the failure rate estimation of SRAM cell

5 总结

本文提出的基于AdaBoost学习的改进的重要性采样算法，以AdaBoost分类器过滤大量无效的采样点，集中对失效区域进行采样;同时，结合了实际分布中均值和方差的依赖关系，基于交叉熵的重要性采样给出更加精确地最有分布逼近公式，并且给出了合理的收敛判定标准，形成了一套完整的系统解决方案.本文提出的算法改善了原来基于MC方法的一类算法普遍存在的精度差、收敛慢等问题.

［1］Takeuchi K，Tatsumi T，Furukawa A.Channel engineering for the reduction of random-dopant-placementinduced threshold voltage fluctuation［C］∥Tech.Dig.of IEDM'97，Washington，DC，1997:841-844.

［2］Agarwal K，Nassif S.Statistical analysis of SRAM cell stability［C］∥Proceedings of the 43th annual Design Automation Conference.New York，USA:IEEE Press，2006:57-62.

［3］Kanj R，JoShi R，Nassif S.Mixture importance sampling and its application to the analysis of sram designs in the presence of rare failure events［C］∥Proceedings of the 43th annual Design Automation Conference.New York，USA:IEEE Press，2006:69-72.

［4］Dolecek L，Qazi M，Shah D，et al.Breakig the simulation barrier:Sram evaluation through norm minimization［C］∥Proceedings of the 2008 IEEE/ACM International Conference on Computer-Aided Design.San Jose，California，USA:IEEE Press，2008:322-329.

［5］Bayrakci A，Demir A，Tasiran S.Fast monte carlo estimation of timing yield with importance sampling and transisitor-level circuit simulation［J］.IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems，2010，29(9):1328-1341.

［6］Wang J，Singhee A，Rutenbar R A，et al.Two fast methods for estimating the minimum standby supply voltage for large srams［J］.IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems，2010，29(12):1908-1920.

［7］Kentaro，Hagiwara，Tsutsui H，et al.Sequential importance sampling for low-probability and highly-dimensional sram yield analysis［C］∥Proceedings of the 2010 IEEE/ACM International Conference on Computer-Aided Design.San Jose，California，USA:IEEE Press，2010:703-708.

［8］Singhee A，Rutenbar R.Statistical Blockade:A novel method for very fast monte carlo simulation of rare circuit events and its application［C］∥Design，Automation Test in Europe Conference Exhibition.Munich，Germany:IEEE Press，2008:235-251.

［9］Freund Y，Schapire R E.Experiments with a new boosting algorithm ［C］∥International Conference on Machine Learning.Bari，Italy:ACM Press，1996:148-156.

［10］Deng，Lih-Yuan.The cross-entropy method:a unified approach to combinatorial optimization，Monte-Carlo simulation and machine learning［J］.Technometrics，2006，48(1):147-148.

［11］Bhowmick，Sanjukta，Victor Eijkhout，et al.Application of alternating decision trees in selecting sparse linear solvers［C］∥Software Automatic Tuning.New York，USA:Springer Press，2010:153-173.

［12］Boyd S，Vandenberghe L.Convex Optimization［M］.Cambridge UK:Cambridge University Press，2004.

［13］Shahid，Mohammed Abdul.Cross entropy minimization for efficient estimation of SRAM failure rate［C］∥Design，Automation＆ Test in Europe Conference＆ Exhibition(DATE).Dresden，Germany:IEEE Press，2012:230-235.