具有状态依赖噪声的随机H∞预演控制

王宏霞，张焕水，陈 欣，俞 立

(1.浙江工业大学信息工程学院，310023杭州;2.山东大学控制科学与工程学院，250061济南)

预演控制问题研究如何利用提前获取的参考信息或扰动信息来设计控制器以改进追踪性能或更好地抑制扰动对系统所造成影响.与人类生活息息相关，具有广泛工程背景，已被用于车辆悬架系统的设计、过程控制、机器人控制以及许多能够提前获取信息的领域［1-2］.起初的研究主要针对确定性系统的最优预演控制问题展开［3］，预演窗口宽度与最优性能显式表达关系的建立［4］，标志着确定最优预演控制问题基本得以解决.至于确定性H∞预演控制问题，直到1999年依然是公开问题［5］.经过多年研究，确定性系统的H∞预演控制问题取得了很大进展［6-8］，但有关随机系统H∞预演控制甚至是时滞系统最优控制问题的相关研究结果［11-12］较少，因此有必要研究随机系统这类更普遍、更具有代表性系统的H∞预演控制问题.

研究的随机系统，特指受到乘积性随机噪声干扰的系统，这类系统具有广泛的应用背景.但与确定性系统具有本质的区别，包括:随机系统不存在传递函数、要考虑适应性［13］、特别的随机极大值原理［14］、解变量成对出现的倒向随机方程［15］、加权矩阵为不定矩阵时仍有意义的最优控制［16］、消失的对偶性［17］.此外，随机系统与确定系统还有许多区别.这些区别，是确定性系统的许多研究思路难以推广、随机系统控制问题难以解决的主要原因.迄今为止，只发现文献［18］应用博弈论，研究了离散时间随机系统的H∞预演追踪问题，它根据可提前获取的参考信息量，引入3种追踪模式来解决问题.但是，由于扰动信息本身不可预演，因而本质上，预演信息的使用是以H2的方式而非H∞的方式.

本文主要研究一类线性随机系统的H∞预演控制问题，研究如何使用可预演的外部扰动信息来设计H∞控制器，改进系统的闭环性能(这种改进相对于标准的H∞控制而言).首先将H∞预演控制问题转化成不定二次型的优化问题;然后结合对策论，根据动态规划的思想，研究不定二次型鞍点存在的条件;基于鞍点给出问题可解的条件和H∞预演控制器;最终利用特征线法提出一种解耦耦合微分与偏微分方程的方法.

对于任意的向量或矩阵M，M'为其转置，M2为M'M，|M|为M的2-范数．对于任意向量函数是标量的维纳过程，因此dw(t)是独立平稳增量过程．E为关于随机过程 dw(t)取数学期望．L2［a，b］表示在区间［a，b］平方可积的所有函数所形成的空间．

1 随机系统H∞预演控制问题

引入具有可预演扰动信息的随机系统为

式中:x(t)∈Rn为系统状态，z(t)∈Rp为待调节信号，u(t)∈Rq为控制输入，v(t)∈Rk为可预演的外部扰动输入．外部扰动输入属于L2［0，T-h］．A，B，C，A0，C，D0，D1是有相容维数的有界时不变矩阵．h(＞0)是可预演时间长度．不妨设dw(t)的均值为0，方差为m．

为简化推导，不失一般性，作以下正交性假设

引入性能指标

参考确定性系统的H∞预演控制问题，随机系统的H∞预演控制问题可以叙述为:考虑系统式(1)～(2)，对于给定的γ＞0，找到一个能够保证性能指标式(4)成立的有限时间域H∞预演控制策略，该策略具有如下结构

式中:PT表示一个给定的半正定矩阵，它反映决策者对终端状态的重视程度，Ft表示某向量函数．

2 问题转化及求解

2.1 问题的转化

为了给出问题的可解性条件及解，把随机H∞预演控制问题转化成一个受随机系统式(1)～(2)约束的最优化问题.

考虑性能指标式(4)，定义

一个控制器u(t)能够保证H∞性能指标式(4)成立当且仅当对于任意的非零v(t)，该控制器都能够保证J0＜0成立．

2.2 问题求解

不论是H∞预演控制问题还是不定二次型的最优化问题，本质上都属于下面的对策问题

其中

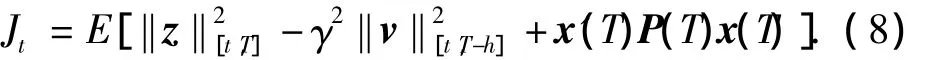
其中u，v分别试图最小化和最大化Jt．这类问题的解，可以通过求解一个Isaacs方程来获取.因此，考虑到预演控制器的结构，有以下结论.

引理1 考虑随机系统式(1)～(2).假设存在几乎处处连续可微的参数 P(τ)，α(τ，s)，β(τ，s1，s2)，τ ∈［t，T］，(τ，s1，s2)∈ ［t，T］× ［0，h］×［0，h］，(τ，s)∈［t，T］×［0，h］，则Jt可等价表示成

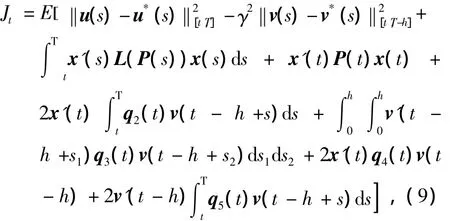
其中

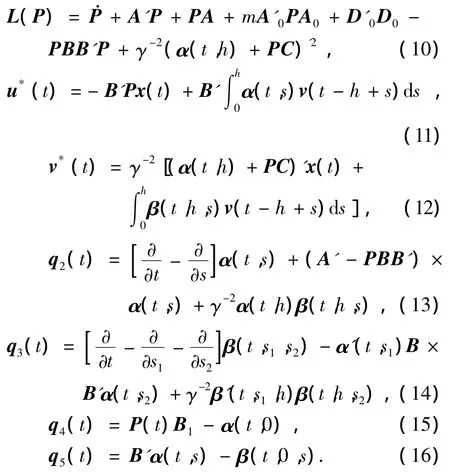
证明 不失一般性，设t＜T-h．

显然有

添加微分零和项式(18)到式(8)的右端可得

参考式(17)后式(20)意味着当t∈［T-h，T］时，

根据Ito微分法则及系统式(1)～(2)，结合

式(19)及下述关系

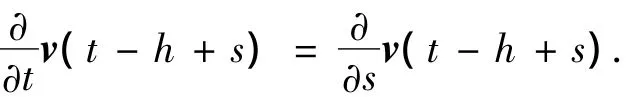
首先计算式(19)右端第4项，然后针对式(19)右端分别关于u(t)，v(t)进行完全平方，最后取期望整理、合并同类项即可得式(9)．

根据引理1，可得出下面结论.

定理1 考虑具有零初始数据的随机系统式(1)～(2)及性能指标式(4).

关于初边值存在有界解

则随机系统H∞预演问题可解，并且式(11)是满足性能指标的H∞预演控制器.

证明 t时刻，当系统的初始数据为零、式(21)～(24)成立，并取u(t)=u*(t)时，从式(9)不难发现Jt＜0成立．同理，当系统从零时刻出发并具有零初始数据时，也有J0＜0，至此，参考问题的转化不难得出，控制器u*(t)满足H∞性能指标式(4).

当h=0时，随机H∞预演控制问题转化成一般的随机H∞控制问题.此时，本文提出的方法能够提供一个基于广义Riccati方程的H∞控制器.具体可概括如下:

推论1 考虑h=0的系统式(1)～(2)及性能指标式(4).如果广义Riccati方程

存在有界解P(t)，则存在一个形如

并能使性能指标式(4)成立的H∞控制器.

3 耦合微分及偏微分方程的解耦求解

观察式(21)～(24)不难发现，这3个方程相互耦合.与求解一般的方程组类似，解耦也是求解式(21)～(24)的首要任务.

该解耦思路很大程度上依赖于 α(t，s)与β(t，θ1，θ2)分别在区域［0，T］× ［0，h］和［0，T］×［0，h］×［0，h］的连续性．因而此处首先假设初值问题式(21)～(24)存在唯一连续解.基于问题的连续性，给出下面的解耦思想.

定理2 给定γ＞0与h＞0．当初边值问题式(21)～(24)存在唯一连续解时，若记

则微分及偏微分式(25)～(27)联合初边值式(23)、(24)存 在 唯 一 连 续 解 βδ(t，θ，θ1)，Pδ(t)，αδ(t，θ)，其中t=t+ δ，h=h- δ，δ＞ 0 可任意小，两初边值问题的解存在如下关系:

由于定理2的证明有赖于下面提到的偏微分方程的特征解法，因此将推迟它的证明.

尽管文献［19］的定理2.1.2只提供了局部解的存在唯一条件，但是与常微分方程的初值问题解的存在唯一定理相似，该定理是分析和求解偏微分初边值问题解的主要依据.有限时间域预演控制问题本质上就是一个偏微分方程的初边值问题.下面将根据特征曲线和积分曲线的关系以及文献［19］的定理来求解的随机H∞预演问题.

且具有终端值P(T)=PT．

观察初值问题式(21)～(24)，当t＞T-h时，由于

P实际上满足可以直接单独求解的H∞倒向微分式(32)，而 α(t，θ)，β(t，θ，θ1)则分别满足以下关系:

其中Ax(t)=A-BB'P，且边值如

使用特征线法［19］依次求解式(33)、(34).值得注意的是:在求解 α(t，θ)，β(t，θ，θ1)时，由于可以先根据式(32)直接求解出P(t)，因此P(t)实际上为已知函数.

偏微分式(33)的特征方程为

其初始参数曲线为

简单计算可得，经过初始曲线的特征曲线为

根据式(37)～(39)，消除参数s，τ可得，由式(33)、(35)决定的积分曲面为

类似的由式(34)、(36)决定的积分曲面为

而当 t∈［0，T-h］时，由于初边值问题式(21)～(24)中3个方程相互耦合，特征线法也无法给出解析解．此时，可以根据定理2提供的思路来求解之.实际上，当 t∈［0，T-h］时，式(25)～(27)中的每个方程的右端，除了左端的未知量外，其它都是已知量，这就保证了可以通过特征线法求解偏微分方程.下面将简述式(25)～(27)的求解过程并给出其解.

根据式(40)可得 α(t，h)，继而可在区间(T-2h，T-h］上求解式(25)．紧接着，根据式(41)，可得β(t，h，θ)，据此在区间(T-2h，T-h］上根据特征线法求解式(26)可得再根据特征线法求解具有初值 β(t，s，0)=C'α(t，s)的式(34)可得

关于区间［0，T-2h］的式(25)～(27)的求解，可以分成1+［(T-2h)/h］个区间倒向进行，其中［.］表示取整运算.鉴于微分方程组结构的一致性，后面剩余的这些区间上的解结构类似，因而可以直接给出，故此处省略它们的求解过程.

定理3 当式(21)～(24)存在连续解时，与其具有相同初始条件的式(25)～(27)存在唯一连续解Pδ(t)(见式(25)、(31)的解)，α(t，θ)(见式(40)、(42))，β(t，θ，θ1)(见式(41)、(43)).

证 明 由式(21)～(24)存在唯一连续解，可以推知式(25)的解存在唯一、偏微分式(25)、(27)的初始曲线及特征方向光滑.又因为在任意初始时刻，偏微分式(26)、(27)中的每个方程关于文献［19］定理2.1.2中的行列式条件总成立，所以，在初始条件的邻域内，定理3的解存在唯一，延拓则可得整个区间上的解.

有了以上的结果，证明定理2.

证 明 除了连续性，证明还需要α(t，θ)，β(t，θ，θ1)在区域［0，T］×［0，h］，［0，T］×［0，h］×［0，h］上的有界性．对于任意的t1∈［0，t］，考虑式(21)，其满足如下关系

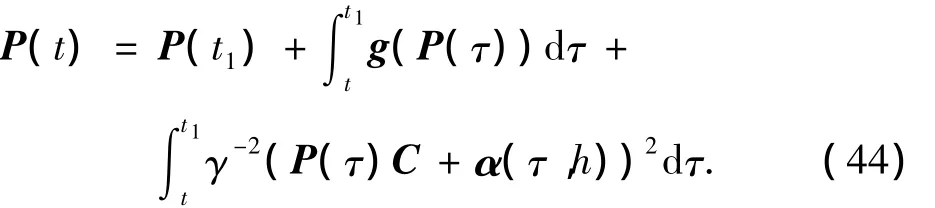
其中

考虑其解满足如下关系

当α(t，s)在区域［0，T］×［0，h］上连续有界时，对于任意的ε ＞0 及 t，t1∈ ［0，T］，总存在δ＞0使得当|t-t1|＜δ时，

记

则

这证明了式(28)，M=4(γ-2T+1)Mα．

根据特征线法所提供的解研究δ，δ1→0时，式(26)、(27)的解 α(t，θ)，β(t，θ，θ1)的极限行为.具体如下:

当|P1-Pδ|＜ ε时

因此，

此外，根据P1，Pδ，α，β 的连续有界性

结合式(50)、(52)、(53)，则可得式(29)．式中M2为一有界正实数，Mα见式(49)．

同理可证式(30).

4 数值例子

为节省空间，将随机系统式(1)～(2)的参数退化到标量，具体如下:

解耦后使用特征线法求解偏微分方程组，可借助Matlab直接求解方程的解.主要涉及dsolve与int两个Matlab命令.由于由此产生的初值问题解非常冗长，仅计算问题在区间［9，10］的控制器.因为式(32)成立，式(21)被解耦成了式(31).利用 Matlab命令 dsolve直接求解式(31)可得P(t)=e10/(3e10-2et)，再根据式(11)可得，在区间［9，10］上，随机 H∞预演控制器u*(t)=2e10/(3e10-2et)．同理，基于区间［9，10］的计算结果，可分别根据 式(25)、(42)、(43)计算区间［8，9］上的P(t)，α(t，s)，β(t，θ，s)，进而根据式(11)计算随机H∞预演控制器u*(t)．这样一个区间接着一个区间倒向推进，则可得整个区间上的控制器.

5 结语

本文给出了随机H∞预演控制问题的可解性条件和显式控制器.由于这些结果基于耦合的微分及偏微分方程给出，本文还提出了一种解耦微分及偏微分方程的方法，该解耦方法适用于几乎所有的线性时滞系统最优控制及H∞控制.值得注意的是，当系统具有控制依赖噪声时，耦合方程的解耦产生的随机Riccati方程中存在微分变量的逆运算，寻求解析解有一定的困难.

［1］BENDER E K.Optimum linear preview control with application to vehicle suspension［J］.Journal of Basic Engineering，1968，90(2):213-221.

［3］SHERIDAN T B.Three models of preview control［J］.IEEE Transactions on Human Factors in Electronics，1966，HFE-7(2):91-102.

［4］MOELIA A A，MEINSMA G.H2control of preview systems［J］.Automatica，2006，42(6):945-952.

［5］BLONDEL V D，SONTAG E D，VIDYASAGAR M，et al.Open problems in mathematical systems and control theory［M］.London:Springer，1999.

［6］ZHANG Huanshui，XIE Lihua，DUAN Guanren.H∞control of discrete-time systems with multiple input delays［J］.IEEE Transactions on Automatic Control，2007，52(2):271-283.

［7］TADMOR G，MIRKIN L.H∞control and estimation with preview-part I:matrix ARE solutions in continuous time［J］.IEEE Transactions on Automatic Control，2005，50(1):19-28.

［8］TADMOR G，MIRKIN L.H∞control and estimation with preview-partII:fixed-sizeARE solutionsin discrete time［J］.IEEE Transactions on Automatic Control，2005，50(1):29-40.

［9］KOJIMA A，ISHIJIMA S.Formulas on preview and delayed control［J］.IEEE Transactions on Automatic Control，2006，51(12):1920-1937.

［10］HAZELL A，LIMEBEER D.An efficient algorithm for discrete-time H∞preview control［J］.Automatica，2008，44(9):2441-2448.

［11］SONG Xinmin， ZHANG Huanshui， XIE Lihua.Stochastic linear quadratic regulation for discrete-time linear systems with input delay［J］.Automatica，2009，45(9):2067-2073.

［12］WANG Hongxia，ZHANG Huanshui.LQ control for Ito-type stochastic systems with input delays ［J］.Automatica，2013，49(12):3538-3549.

［13］YONG Jiongmin，ZHOU Xunyu.Stochastic controls:Hamiltonian systems and HJB equations［M］.New York:Springer，1999.

［14］PENG Shige.A general stochastic maximum principle for optimal control problems［J］.SIAM Journal on Control and Optimization，1990，28(4):966-979.

［15］严加安，彭实戈，吴黎明，等.随机分析选讲［M］.北京:科学出版社，1997.

［16］CHEN Shuping，LI Xunjing，ZHOU Xunyu.Stochastic linear quadratic regulators with indefinite control weight costs［J］.SIAM Journal on Control and Optimization，1998，36(5):1685-1702.

［17］ZHANG Huanshui，SONG Xinmin.New estimator and duality of control for multiplicative noise systems with applications to packet dropping and multiple input delay systems［C］//2009 IEEE International Conference on Control and Automation.Christchurch:IEEE，2009:75-80.

［18］GERSHON E，LIMEBEER D，SHAKED U，et al.Stochastic H∞tracking with preview for statemultiplicative systems［J］. IEEE Transactionson Automatic Control，2004，49(11):2061-2068.

［19］陈祖墀.偏微分方程［M］.合肥:中国科学技术大学出版社，2002.