自适应提升小波在干涉高光谱压缩中的应用
温 佳,马彩文,赵军锁,王彩玲
(1.中国科学院软件研究所天基综合信息系统重点实验室,100190北京;
2.中国科学院西安光学精密机械研究所,710119西安;3.西安石油大学计算机学院,710065西安)
干涉高光谱技术在航空航天遥感领域中是一种很有实用价值的技术,通过这种技术可以获得观测目标的光谱信息与空间信息,因此在气象、军事、环境监测和地质等领域都有较广泛的应用.随着干涉高光谱仪在中国“嫦娥”探月卫星和近期环境探测卫星中的成功搭载,干涉高光谱的数据压缩成为近年来的研究焦点之一.
干涉高光谱图像数据是一种三维图像数据,其海量数据造成在数据存储和有限带宽信道上的传输有一定程度的困难,所以针对其数据本身特点设计出适用于干涉高光谱数据的高效数据压缩方法十分必要.
近年来,越来越多的科学家针对干涉高光谱数据特性提出了有效的压缩算法,基于谱间DPCM和整数小波的超光谱图像无损压缩在2008年提出[1],针对干涉高光谱图像帧间不稳定移位的改进变换算法在2011年提出[2],针对干涉高光谱图像帧间相关的自适应光程差算法在2011 年提出[3].
本文在文献[2]基础上,考虑到每帧 LASIS干涉高光谱数据均存在幅值较大的竖直干涉条纹,并且干涉条纹在每帧之间不存在移位,而除干涉条纹之外的背景图像均存在方向性移位的特点,尝试在帧序列方向采用不同方向自适应得到最佳预测值,并且改变传统三维提升小波的变换顺序以消除干涉条纹所造成的冗余以达到更好的压缩效果和压缩性能.
1 干涉高光谱图像的数据特性
干涉高光谱图像数据具有与其他图像不同的特性.图1为LASIS干涉高光谱图像三维示意图.由于其特殊的推扫式成像原理,干涉高光谱图像具有明显的竖直干涉条纹存在.

图1 LASⅠS干涉高光谱图像数据
由图1可以明显看出干涉高光谱与一般的普通图像存在明显差异,干涉高光谱图像具有如下特点:
1)光的干涉是成像原理,干涉高光谱图像并非光的直接成像,而是干涉图像.图像内存在明显的竖直干涉条纹,这些竖直的干涉条纹随着光线调制程度的改变在不同位置呈现不同的强度.
2)干涉高光谱图像是三维数据,具有多维方向的相关性.在联合调制干涉高光谱图像中,目标是一个整体的推扫平移过程,帧内图像具有空间信息,在图像帧间存在着平移现象(干涉条纹不存在).
2 提升小波变换
Haar变换的提升版本是最简单的提升小波变换之一,称为 S 变换[4].
S变换步骤如下:

式中:x[n]为输入信号,s[n]为提升小波变换后的低频信号,d[n]为提升小波变换后的高频信号,⎿」表示向下取整运算.经过S提升后的低频信号与原始输入信号的动态范围相同,高频信号将变得很小,Said等[5]之后又提出了S+P(S变换 +Predication),Zandi等[6]提出的 TS变换是基于梯形结构的比S变换具有更高消失矩的整数小波变换.Sweldends等[7-11]在 Donoho 等[12]的基础上又提出了采用提升框架的第二代小波变换结构之后,Calderbank等[13]提出了基于提升格式的整数小波变换.
提升小波变换分为3个步骤:
1)lazy变换;
2)预测 (predication);
3)更新 (update).
第一步lazy变换是把数据分为偶数集合和奇数集合

第二步预测是用偶数集来预测奇数集,将产生的误差作为高频系数.

第三步更新是用这些高频系数来更新偶数集合作为低通系数.

式中:si[n]为第i层原始提升的低通分量,di[n]为第i层对偶提升的高通分量.
3 根据干涉高光谱特性改进的自适应方向角三维提升小波变换
由于干涉多光谱图像帧与帧之间有很强的方向性,并且三维LASIS图像序列帧与帧之间的平移量是不稳定的,实验数据表明一般相邻帧之间的平移在1~3列不等.LASIS通常搭载在飞行器上进行探测,运用大孔径静态干涉成像光谱仪面阵探测器依靠推扫获得二维的空间信息与一维的光谱信息,形成三维立体图像数据.在干涉高光谱图像中具有明显的竖直干涉条纹,且竖直干涉条纹的位置固定,不存在移位现象,竖直干涉条纹中含有光谱信息,并且干涉高光谱图像帧间具有明显平移,方向与探测器推扫方向基本一致,然而由于非匀速的推扫,平移方向存在抖动.
本文采用传统5/3提升小波,在帧内的行方向和列方向直接采用传统5/3提升小波进行小波变换:


为了提高运算速度,对于r×c×f的LASIS三维数据,在列方向的提升小波变换之前,先将图像拼接成[r,c×f]的2维矩阵,拼接方式如图2所示.新生成的2维矩阵有c×f列,每列含有r个像素值,将新生成的[r,c×f]二维矩阵对应式(2)中的x变量,将行数r对应公式(2)的变量n,之后按照式(2)生成s0[n],d0[n]的二维矩阵如图 3 所示.将生成的 s0[n]、d0[n]按照式(5)、(6)进行一次一维垂直方向的提升小波变换,结果如图4所示,之后再把新生成的矩阵还原成原来的[r,c,f]的三维矩阵,即可完成对 r× c×f的LASIS三维数据的列方向提升小波变换.水平方向提升小波变换按照与之类似流程完成.对于帧序列方向的提升小波变换,则把三维LASIS数据拼接成[f,r×c]的2维矩阵,每k行的r×c个像素值是原始三维矩阵的第k帧的帧内r×c个像素按水平方向拼接而成,k=1,2…f,由于LASIS数据帧间的方向特性,拼接后的2维[f,r×c]矩阵如图5所示.新生成的2维矩阵有r×c列,每列含有f个像素值,按式(2)将新生成的[f,r×c]二维矩阵对应式(2)中的x变量,将行数f对应式(2)的变量n,之后按照公式(2)生成的s0[n]、d0[n]为的二维矩阵如图6所示.将生成的 s0[n]、d0[n]按照式(5)、(6)进行一次一维垂直方向的提升小波变换,结果如图7所示.

图2 垂直方向提升小波变换LSSIS 数据拼接示意

图3 垂直方向提升小波变换中s0[n]和d0[n]示意

图4 垂直提升小波变换后LASⅠS数据示意

图5 帧间提升小波变换LASⅠS数据拼接示意

图6 帧间方向提升小波变换中s0[n]和d0[n]示意

图7 帧间提升小波变换后LASⅠS数据示意
之后再把新生成的矩阵还原成原来的[r,c,f]的三维矩阵,即可完成对r× c× f的 LASIS三维数据的帧序列方向提升小波变换.
由于干涉高光谱图像的成像原理所导致其自身的特殊性质,对于帧序列方向,由于干涉高光谱图像数据在帧间存在1~3的移位,这在图5中可以明显看到,况且在进行完一级提升小波变换之后,再做下一级提升小波变换时,帧间的移位会有加倍的变化,这一点在图5、7的对比中也可以明显看到.
直接对上述矩阵在垂直方向做提升小波变换在第二步的预测步骤并不能得到很好的结果,所得的高频系数会偏大.本文针对LASIS三维数据的帧序列方向专门提出一种自适应预测方向角的提升小波变换以适应LASIS帧间特有的方向性特点.
在预测步骤采用5/3的提升小波变换d1[n]=,d0[n]实际上是夹在 s0[n]、s0[n+1]中间的层,由于帧间1 ~ 3移位的存在,体现在d0[n]、s0[n]、s0[n+1]上为:s0[n]为了与d0[n]在垂直方向对应,应向左移动1 ~3位,s0[n+1]为了与d0[n]在垂直方向对应,应向右移动1~3位.
s0[n]和 s0[n+1]与 d0[n]最佳匹配的移位各有4种可能,其两两组合共有16种可能性存在,这样进行预测步骤会得到16种可能的d1i[n],i=1,2,…,16,将d1i[n]的每一行的r× c个像素值的绝对值相加,会得到16个[f/2,1]的列,将其转置成行并用一个[16,f/2]的二维矩阵d1_sum存储,d1_sum有f/2列,每一列含有16种可能的值,保存每列最小值的索引值,f/2列会产生f/2个index索引值,index(k)∈[1,16],k=1,2,…,f/2.如此可以快速的得到每帧的上一帧和下一帧对应的移位最佳组合,新生成的d1[n]的每k行为 d1index(k)的第k行,k=1,2,…,f/2.在信道传输数据时,索引值需要与编码后的码字一起传输.
LASIS干涉高光谱三维数据由于竖直干涉条纹的存在并且有较大的幅值,如果为了提高运算速度把提升小波的预测步骤中的 d0[n]、s0[n]作为整体进行运算,会影响到帧间的方向性,因为尽管大部分背景像素存在整体的方向性移位,但是竖直的干涉条纹不存在移位并且具有较大的幅值.因此,在这里不采用传统的对称三维小波变换,先对LASIS数据进行3级的一维垂直方向的提升小波变换,可以基本上消除掉LASIS数据中特有的竖直干涉条纹所带来的影响,图8所示为对16帧LASIS数据进行3级竖直方向提升小波变换后的3帧小波系数示意图.
由图8可见,在低频分量依然存在不移位的干涉条纹,而高频分量的干涉条纹冗余已基本消除,由于本文采用拼接后整体进行运算,如果直接对3级垂直方向提升小波变换后的系数进行帧序列方向预测,并不能得到最佳的移位索引.因此本文对含有干涉条纹冗余的低频分量和干涉条纹冗余以基本被消除的高频分量分别进行3级自适应帧序列方向的提升小波变换,这样会分别得到存在干涉条纹影响的最佳移位索引和不存在干涉条纹影响的最佳移位索引,最后再将所得的结果进行3级水平方向的提升小波变换.
本文提出自适应预测提升小波变换算法的流程图如图9所示.

图8 三级垂直方向提升小波变换后小波系数示意图

图9 本文提出算法的流程图
4 实验结果
对两组512×288×16的12 bvit LASIS三维数据在bpppb(比特/像素/波段)=0.1~0.3进行实验,结果如表1~2所示.

表1 不同bpppb下LASⅠS数据1的信噪比 dB

表2 不同bpppb下LASⅠS数据2的信噪比 dB
由表1、2可知,使用本文提出的变换方法相对于传统提升小波变换方法,在经过3DSPECK编码后,在给定编码比特数目即压缩比一定的情况下重构图像可以获得更高的信噪比.图10、11显示了1组512×288×16的LASIS干涉高光谱图像数据经过本文提出改进的变换方法与传统三维对称提升小波变换和2011年提出的自适应小波变换[2]后经过3DSPECK编码后重构结果的比较.将3种方法得到的LASIS重构干涉高光谱数据帧通过后期处理得到LSMIS(Large Spatially Modulated Interference Spectral Image)干涉图后,还原光谱曲线如图12所示,还原光谱曲线与原始光谱曲线的均方误差如表3所示.

图10 LASⅠS原始数据

图11 比特率为0.3时3种不同方法的恢复图像
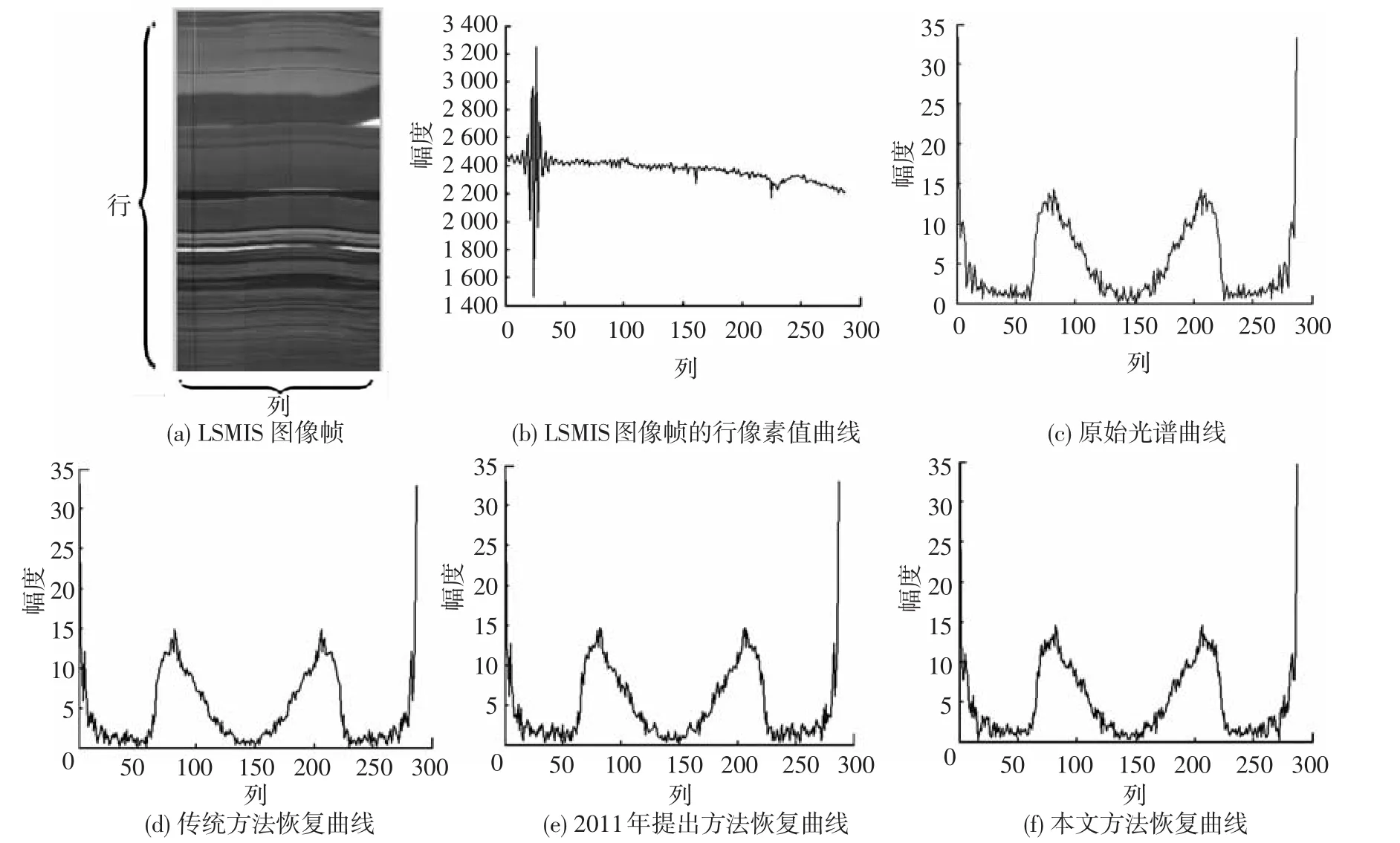
图12 3种不同方法的恢复光谱曲线

表3 不同方法下还原光谱曲线的均方误差
5 结语
从本文实验结果可以明显看出如果仍然运用传统小波变换顺序进行帧序列方向的自适应方向角预测,对高频小波系数间方差减小并不明显,因为干涉条纹的存在影响了整体自适应方向预测的结果,通过本文方法消除垂直方向冗余并且对含有干涉条纹冗余的低频子带和不含干涉条纹冗余的高频子带分别进行自适应方向预测后,高频子带的小波系数间方差得到了大幅度改善.将提出的小波变换方法与传统方法产生的小波系数在指定码率下进行3DSPECK编码,大量实验数据表明本文提出的改进方法的重构图像可以获得更高的信噪比,且后期处理得到的光谱曲线相对于原始光谱曲线具有更小的均方误差.
[1]吴冬梅,王军,张海宁.基于谱间 DPCM和整数小波的超光谱图像无损压缩[J].光子学报,2008,37(1):156-159.
[2]WEN J,MA C W,SHUI P L.A 3D non-linear orientation prediction wavelet transform for interference hyperspectral images compression[J].Optics Communications,2011,284(7):1770-1777.
[3]WEN J,MA C W,SHUI P L.An adaptive OPD and dislocation prediction used characteristic of interference pattern for interference hyperspectral image compression[J].Optics Communications,2011,284(20):4903-4909.
[4]BLUME H,FAND A.Reversible and irreversible image data compression using the S.transform and Lempel-Ziv coding[C]//Proceedings of SPIE Conference on Medical Imaging.Newport Beach:CA,1989,1091:2.
[5]SAID A,PEARLMAN W A.An image multiresolution representation for lossless and lossy compression[J].IEEE Transactions on Image Processing,1996,5(9):1303-1310.
[6]ZANDI A,ALLEN J,SCHWARTZ J E.Compression with reversible embedded wavelets[C]//Proeeedings of IEEE Data Compression Conference.Snowbird:DCC,1995:212
[7]SWELDENS W.The lifting seheme:a new philosophy in biorthogonal wavelet constructions[C]//Proceedings of SPIE Conference on Wavelet Applications in Signal and Image Processing.San Diego:CA,1995,2569:68.
[8]SWELDENS W,SHROEDER P.Building your own wavelets at home[R].Columbia:University of South Carolina,1995.
[9]SWELDENS W.The lifting scheme:a custom-design construction of biothogonal wavelets[J].Applied and Computational Harmonic Analysis,1996,3(2):186-200.
[10]SWELDENS W.The lifting scheme:construction of second generation wavelets[J]. SLAM Jounalof Mathematical Analysis,1997,29(2):511-546.
[11]DAUBEEHIES I,SWELDENS W.Factoring wavelet transforms into lifting steps[J].Joumal of Fourier Analysis and Applications,1998,4(3):247-269.
[12]DONOHO D L.Interpolating wavelet transform[M].PaloAltoCounty:DepartmentofStatistics,Standford University,1992.
[13]CALDERBANK A R,DAUBECHIES I,SWELDENS W.Wavelet transforms that map integers to integers[J].Applied and Computational Harmonic Analysis,1998,31(5):332-369.

