常微分方程通解、特解、所有解的区别与联系

刘雄伟， 王 晓

(国防科技大学理学院，湖南长沙410073)

在国内的高等数学教材与常微分方程教材中，对于n阶常微分方程

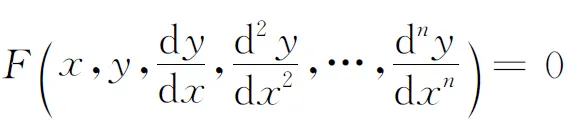
(1)

关于通解、特解通常定义如下[1,2]：

如果包含有n个相互独立的任意常数C1,C2,…,Cn的关系式

Φ(x,y,C1,C2,…,Cn)=0

(2)

确定的函数y=φ(x,C1,C2,…,Cn)是(1)的解，则称(2)为(1)的通解.通过初值条件

y(x0)=y1,y′(x0)=y2,…,y(n-1)(x0)=yn

(3)

确定通解中的任意常数后，得到的解Φ(x,y)=0称为(1)的特解.

对于非数学专业的学生来说，在高等数学课程的常微分方程学习过程中，通解、特解、所有解的定义及相互关系，二阶齐次线性微分方程降阶法和二阶常系数非齐次线性微分方程所设特解的处理方式，一直是学生在学习过程中容易产生困惑的内容.为了更好的理解和求解常微分方程，关于常微分方程的通解、特解和微分方程的所有解的基本概念和求解过程中的一些处理方式有几点需要特别注意.

(i) 通解并不一定包含微分方程的所有解.

例如[1]，y=sin(x+C)是微分方程

(4)

的通解，但y=±1也是(4)的解，显然不包含在通解中，即通解不包含方程的所有解.因此，在做练习时，应该注意求解微分方程与求微分方程通解的差别.一般来说，求解微分方程应该将满足微分方程的所有解求出，而求通解只需要求得一个包含与微分方程阶数相同个数的、相互独立的任意常数的解即可.同时通解也不唯一，如微分方程[3]

xy′-3y=0

(5)

在全体实数范围内通解可以为y=Cx3，也可以是

值得注意的是，一般来说微分方程的通解可以包含它的所有解，或者在满足一定的条件下，微分方程的通解会包含微分方程所有解[4].但是并不是所有微分方程都有通解，有些微分方程只能通过数值方法来求解.

(ii) 由(1)和(3)确定的初值问题的特解不唯一.

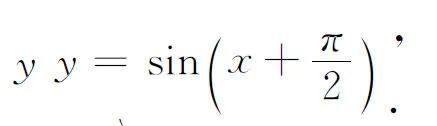
其中A可以是任意确定的常数.但是在x>0的范围内则特解是唯一的.

(iii) 通解中的任意常数“不任意”.

在常微分方程通解的定义中强调相互独立的任意常数，意指在通解中取一组给定的常数得到的函数都为对应常微分方程的解.其实，任意常数并非可以任意取值，如siny+cosx=C是常微分方程cosydy=sinxdx的通解，此时C取大于2的值就没有意义了[5].所以任意常数并不是一定可以取遍任意实数的，而且也不要求它一定要取遍实数，这个任意性应该在使得通解关系式有意义的范围内体现.

(iv) 包含有m(0

如y=C1ex+C2e-x是微分方程y″-y=0的通解，而对于微分方程y‴-y′=0，它既不是通解，也不是特解，而是它的一组解.

(v)在求微分方程的通解时，只需要得到符合定义(2)的微分方程解即可.

在一般的高等数学教材中，在介绍利用降阶法求解二阶齐次线性微分方程时，采取了对刘维尔公式推导过程中不定积分的任意常数取零和利用线性微分方程解的结构求解二阶常系数非齐次线性微分方程特解时，当λ和α±βi为对应的齐次线性微分微分方程的特征根时，将所设特解乘以xk形式的作法[1].即推导刘维尔公式的过程中，中间的不定积分取其他常数也可以得到一个与已知特解线性无关的解；同样，在设二阶常系数非齐次线性微分方程的特解时，不乘以xk，直接设多项式为Qm+1(x)(λ和α±βi为单根时)或者Qm+2(x)(λ为二重根时)也可以，这时候对应的常数项(单根)或者常数项与一次项可以任意取，只不过教材中采取了特殊值为零的作法.这样做的目的是为了简化计算，是完全符合求二阶线性微分方程通解要求的.

例1求微分方程x2y″+xy′-y=0的通解.

解这是一个欧拉方程，也是二阶齐次线性微分方程.容易看出微分方程有特解y=x，且据题意可知x≠0，由刘维尔公式，并将其中的积分常数取0，有

因此可得微分方程的通解为

如果中间过程加上任意常数，则有

容易验证，C,D取任意确定的常数，y2都是微分方程的一个与y=x线性无关的特解.

例2求微分方程

y″-2y′-3y=e3x(1+x2)

(6)

的通解.

解这是一个二阶常系数非齐次线性微分方程，(6)的右边项属于第一种类型eλxPm(x)，并且λ=3是(6)对应的齐次线性微分方程的单根，因此在教材[1]中设其特解形式为

f(x)=xe3x(a0+a1x+a2x2).

将其代入(6)，得特解为

(7)

其实(6)的特解也可以设为

g(x)=e3x(a0+a1x+a2x2+a3x3),

将g(x)代入(6)，有

4a1+2a2+(8a2+6a3)x+12a3x2=1+x2，

由此得(6)的特解为

(8)

容易验证(8)是(6)的解，而(7)只是a0=0中间的一个.而根据线性微分方程组的结构，其实(8)中的a0取任意确定的常数都构成(6)的一个特解，因此(6)对应的齐次线性方程的通解加上(8)都构成(6)的通解.

值得注意的是，对于常微分方程通解的定义，在不同国家的一些教材中有不同的定义[6]，比较典型的定义是本文讨论的定义和定义通解是“全部解的解族”的定义.我们这里讨论的是我国高等数学教材中通常给出的通解定义.

[参 考 文 献]

[1] 朱健民，李建平.高等数学[M].北京：高等教育出版社，2007：400-401.

[2] 金银来，邱建龙，郭政.常微分方程[M].北京：电子工业出版社，2011：4-5.

[3] 管志成，李俊杰.常微分方程与偏微分方程[M].杭州：浙江大学出版社，2001：5-5.

[4] 钱明忠，陈友朋.常微分方程的通解[J].高等数学研究，2007，10(4)：106-108.

[5] 吴全荣.“微分方程的通解”探析[J].漯河职业技术学院学报，2009，8(2)：130-132.

[6] 张义富.关于常微分方程通解定义的讨论[J].大学数学，1989(1)：53-57.