中部铰支加固的细长压杆稳定性研究

黄开志 陈小亮 郑安节

(重庆科技学院数理学院，重庆 401331)

一些文献［1－4］采用了统一的计算模型，得到了传统意义上常见的各种细长压杆临界压力计算公式。工程实际中，为了增加压杆的稳定性，常在压杆中部适当位置附加某些约束。对这类压杆，材料力学教材仅针对在压杆中点加固的某些特殊情况，予以了极为简单有限的介绍，没有建立各种常见约束情况下，在压杆中部任意位置加固时，临界压力的统一求解方法，给工程应用带来诸多不便。文献［5－6］虽有研究，但研究的类型也极单一，难以为工程实际提供更高的使用价值。

本文拟对中部任意位置增加一个铰支加固的9种细长压杆，建立临界压力特征方程，求解长度因数的数值解，并确定中部支承的合理位置及最小长度因数。

1 公式推导

设长为l、中部任意位置x处铰支加固的细长压杆的抗弯刚度为EI，其处于微弯曲平衡状态，其受力和变形情况如图1所示。

图1 整体微弯曲平衡状态

1.1 变形关系

1.1.1 变形方程

AB段即0≤x1≤x时，弯矩方程:

挠曲线近似微分方程:

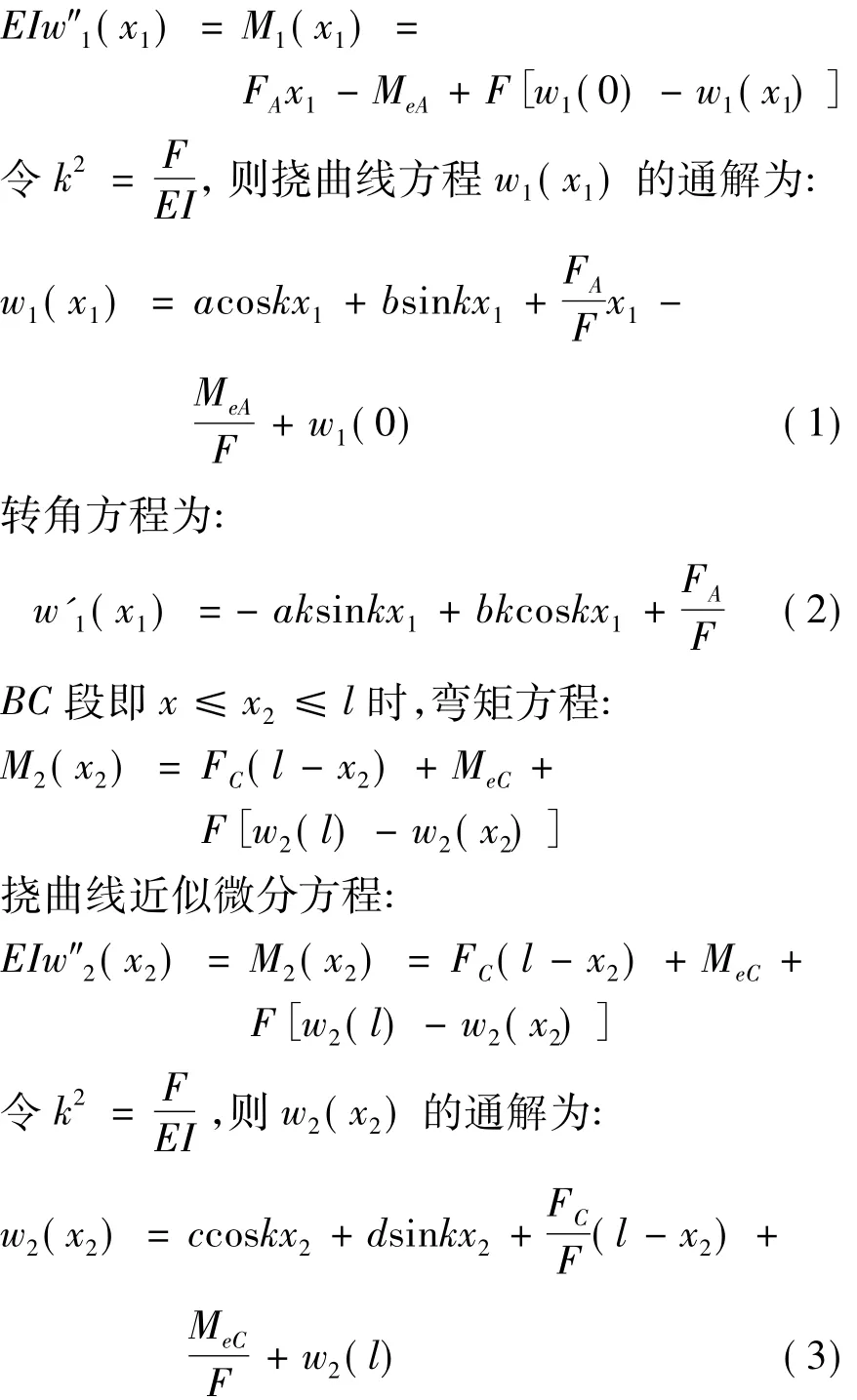
1.1.2 变形边界条件

令式(1)、(2)中的x1=0，则压杆A端的变形满足

压杆在B点满足w1(x)=0，即令式(1)中的x1=x，得:

压杆在B点转角连续，即w′1(x)-w′2(x)=0，由式(2)、(4)得:

压杆在B点满足w2(x)=0，即令式(3)中的x2=x，得:

令式(3)、(4)中的x2=l，则压杆C端的变形满足

各种支承情况下的变形约束条件见表1。

1.2 静力学关系

1.2.1 静力平衡方程

1.2.2 静力约束条件

各种支承情况下的静力约束条件见表1。

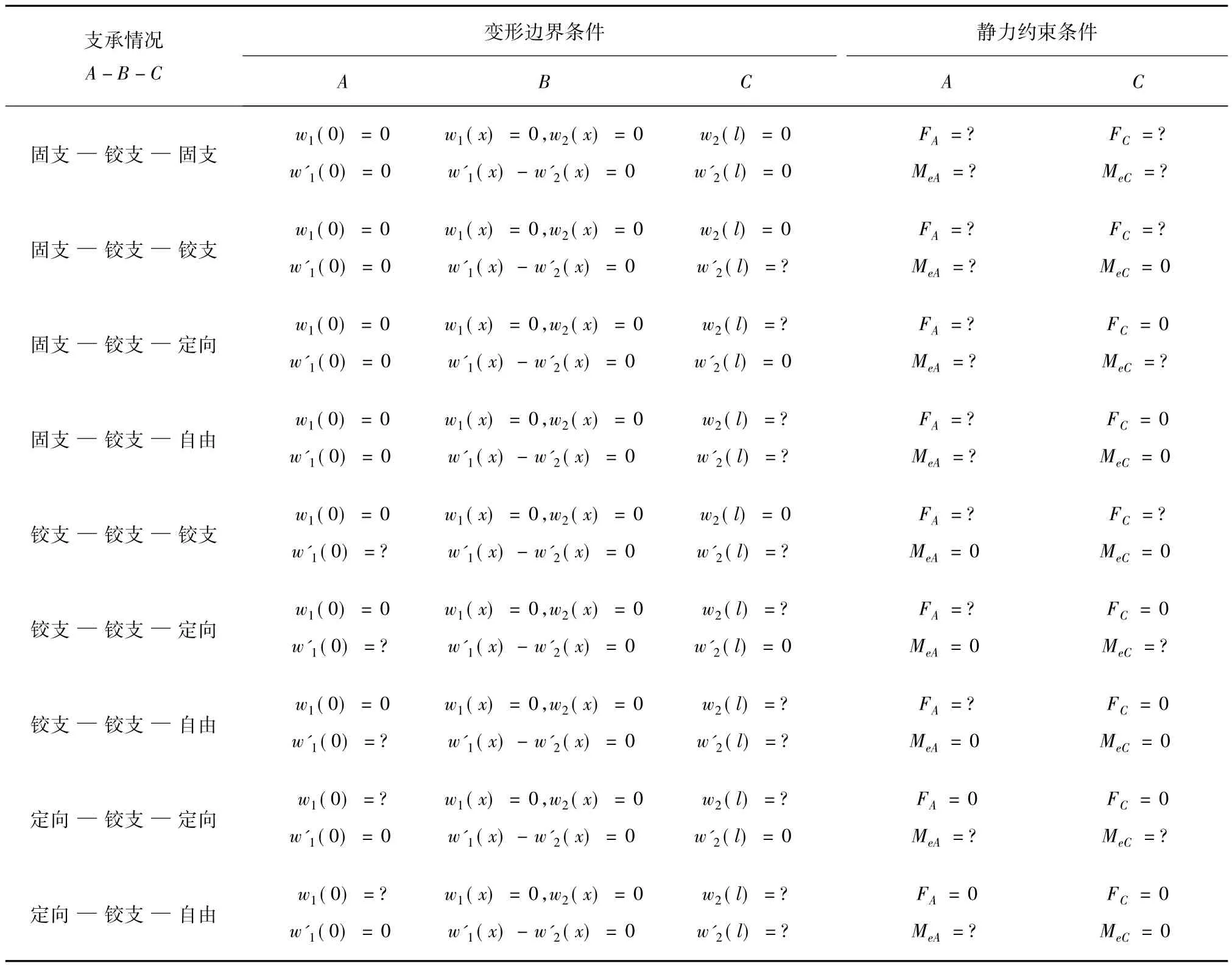
表1 各种支承情况下的变形约束条件和静力约束条件

1.3 特征方程

根据表 1所述的不同约束情况，a、b、c、d和表1中的4个“?”共8个初参数，可由式(5)—(12)求解，在求解时应注意表1中为零的条件。

1.3.1 固支 —铰支 —固支

结合表1，由式(5)—(12)确定了一个关于初参数 a、b、c、d、FA/F、MeA/F、FC/F、MeC/F 的齐次线性方程组，其有非零解的充要条件是系数行列式为零，即求解压杆临界压力的特征方程为:

1.3.2 固支 —铰支 —铰支

结合表1，由式(5)—(12)确定了一个关于初参数 a、b、c、d、FA/F、MeA/F、FC/F、w′2(l) 的齐次线性方程组，其有非零解的充要条件是系数行列式为零，即求解压杆临界压力的特征方程为:

1.3.3 固支 —铰支 —定向

定向支承仅对压杆在支承处的转角作刚性约束，即在该支承处压杆的转角必为零，而不限制压杆的挠度和轴向位移。

结合表1，由式(5)—(12)确定了一个关于初参数 a、b、c、d、FA/F、MeA/F、MeC/F、w2(l) 的齐次线性方程组，其有非零解的充要条件是系数行列式为零，即求解压杆临界压力的特征方程为:

1.3.4 固支 —铰支 —自由

结合表1，由式(5)—(12)确定了一个关于初参数 a、b、c、d、FA/F、MeA/F、w2(l) 、w′2(l) 的齐次线性方程组，其有非零解的充要条件是系数行列式为零，即求解压杆临界压力的特征方程为:

1.3.5 铰支 —铰支 —铰支

结合表1，由式(5)—(12)确定了一个关于初参数 a、b、c、d、FA/F、FC/F、w′1(0)、w′2(l) 的齐次线性方程组，其有非零解的充要条件是系数行列式为零，即求解压杆临界压力的特征方程为:

1.3.6 铰支 —铰支 —定向

结合表1，由式(5)—(12)确定了一个关于初参数 a、b、c、d、FA/F、MeC/F、w′1(0)、w2(l) 的齐次线性方程组，其有非零解的充要条件是系数行列式为零，即求解压杆临界压力的特征方程为:

1.3.7 铰支 —铰支 —自由

结合表1，由式(5)—(12)确定了一个关于初参数 a、b、c、d、FA/F、w′1(0)、w2(l) 、w′2(l) 的齐次线性方程组，其有非零解的充要条件是系数行列式为零，即求解压杆临界压力的特征方程为:

1.3.8 定向 —铰支 —定向

结合表1，由式(5)—(12)确定了一个关于初参数 a、b、c、d、MeA/F 、MeC/F、w1(0) 、w2(l) 的齐次线性方程组，其有非零解的充要条件是系数行列式为零，即求解压杆临界压力的特征方程为:

借助软件化简得:sin kl=0

1.3.9 定向 —铰支 —自由

结合表1，由式(5)—(12)确定了一个关于初参数 a、b、c、d、MeA/F 、w1(0) 、w2(l) 、w′2(l) 的齐次线性方程组，其有非零解的充要条件是系数行列式为零，即求解压杆临界压力的特征方程为:

借助软件化简得:cos kl=0

1.4 长度因数及临界压力

对1.3.1 —1.3.7节中的支承情况处理如下:

(a)在上述的特征方程中令x=ml，用软件如maple12等展开，得到仅含参数m和kl的隐式方程f(m，kl)=0。

(b)绘制f(m，kl)=0曲线，则0≤m≤1且kl为最小正数段曲线即为所求m－kl曲线，结果见图2。

图2 特征方程曲线

显然，1.3.8 节、1.3.9 节中的长度因数与 m 取值无关，分别为1和2。

表2 不同m值对应的长度因数μ

2 结语

压杆的临界状态本质是微弯曲平衡状态，在推导上述特征方程时，把约束反力和相应的变形同时作为初参数，对整个压杆建立了统一的变形方程和静力平衡方程，符合压杆处于临界状态的真实情况。

本文全面系统地给出了在中部任意位置增加一个铰支加固时，共9种常见细长压杆的临界压力的特征方程。借助软件，求得了长度因数的数值解，确定了中部支承的合理位置及最小长度因数。

［1］李有兴，肖芳淳.用弯剪矩阵法确定压杆临界力的教学研究［J］.力学与实践，1995，17(1):69-71.

［2］冯贤贵.细长压杆临界压力的统一推导［J］.力学与实践，2003(4):65-67.

［3］曾生桥.细长压杆临界压力欧拉公式的另一种统一推导［J］.常州工学院学报，2007，20(2):48-50.

［4］董冠文，李宗义，赵彦军，等.压杆稳定临界力欧拉公式统一推导［J］.武汉工程大学学报，2012，34(12):71-74.

［5］蒋学东，李小平.连续压杆稳定性初参数法的研究［J］.江苏工业学院学报，2003，15(2):43-45.

［6］倪晓博，许笛.连续梁式压杆固有频率与稳定性分析［J］.科技创新导报，2010(5):112.