金融危机前后国债收益率曲线变动的潜在因素分析

杨婉茜， 成力为

（大连理工大学经济学院，辽宁大连116024）

收益率曲线是分析宏观经济趋势，为固定收益证券和利率衍生品定价，管理利率风险等的基本工具。收益率曲线的变动是市场对诸如贷款供需、失业、通胀、经济周期、货币政策变化和市场参与者的活动等一些经济变量的预期发生改变的结果，比债券价格反映更多的未来信息。2008年美国金融危机爆发后，人民币升值的预期导致大量资金流入使通胀压力上升和全球经济衰退加剧了我国经济增长动力不足，这必然影响到收益率曲线的形状和移动方式，从而进一步影响微观经济主体对风险管理工具的选择。当前各种风险管理工具日趋丰富，随着利率风险管理工具越来越复杂，利率风险管理的成本也越来越高，对不同宏观经济条件下收益率曲线移动方式的研究有助于微观经济主体平衡风险管理工具应用的成本和收益。为此，本文研究金融危机前后中国宏观经济发生显著变化的背景下，影响收益率曲线移动方式的潜在因素结构，并据此提出应根据潜在因素结构特征选择不同的风险免疫工具，这具有一定的现实意义和应用价值。

收益率曲线表达了同质债券（具有同样风险和流动性）的到期收益率与期限的关系，它反映了利率的期限结构即零息票债券的到期收益率与剩余期限的关系。利率期限结构的相关研究大致可以分为三类。第一类，研究利率期限结构的静态拟合，主要方法包括样条插值和参数模型。其中，Nelson和Siegel的NS参数模型及其扩展Svensson的SV模型因简易性、灵活性和模型参数具有明显的经济含义［1］［2］［3］，得到多国央行的广泛应用［4］。第二类，利用宏观-金融模型研究利率曲线的潜在因子与宏观经济变量的关系［5］［6］。Orphanides、Hördahl与Rudebusch等将宏观经济因素加入到收益率的预测模型中，证明宏观经济因素对收益率变化 存在客 观影响［7］［8］［9］［10］。第三类，研究应用利率期限结构套期保值和管理利率风险［11］［12］。Diebold认为动态NS模型能为美国债券提供相对更好的套期保值效果［13］；余文龙与王安兴将动态NS向量久期应用于中国国债被动管理，说明该技术对于债券管理具有应用潜力［14］；刘艳萍等应用NS模型管理商业银行的利率风险，发现其免疫效果优于传统久期缺口模型［15］。

现有研究存在以下问题：一是静态拟合收益率曲线一般把最小化国债价格误差作为目标函数，然而目标函数的选择应该由不同经济主体特定的目的决定。宏观经济政策制定者，更关心的是货币政策的政策效应，而利率是重要传导工具，收益率误差作为目标函数包含更直接的未来信息，其精确估计对政策效应的预测至关重要。对于一般的市场投资者，由于债券的买卖差价包含更多的即期信息，债券价格误差作为目标函数更符合市场投资者的需要。二是认为各个时期不同的宏观经济变量（产出、通胀等）对利率期限结构潜在因子的影响是相同的，没有考虑经济条件发生较大变化时不同宏观经济变量（产出、通胀等）对利率期限结构各潜在因子影响的大小发生了较大变化，这进一步又影响到利率风险免疫工具的选择。三是选择管理风险和套期保值的工具时也没有考虑调整成本和收益的关系，特别是商业银行选择避险工具匹配资产和负债时，调整的难度和成本必须和相应的收益取得平衡。本文的主要创新点：考虑到金融危机前后中国货币政策的重大变化以及主要宏观经济变量与收益率曲线的关系，用主成分分析方法分析了金融危机前后收益率曲线变动的潜在因子结构，并据此提出风险免疫工具选择的建议。

本文首先用NS模型估计2001年11月～2013年4月上海证券交易所国债的收益率曲线；然后提取2001年11月～2007年12月与2008年1月～2013年4月两个时段收益率曲线移动的潜在因素，以证实模型选择的合理性，同时验证金融危机后明显变化的宏观经济是否为影响收益率曲线移动的关键潜在因素；最后根据潜在因素的结构给出风险免疫建议。

一、收益率曲线估计

1.即期利率模型及目标函数选择

即期利率是零息票债券的到期收益率，然而我国国债市场上零息票债券匮乏，绝大多数是周期付息的息票债券，而计算息票债券的到期收益率不同于零息票债券，它采用的是相同的贴现因子贴现每期现金流，但可以将息票债券的现金流看成零息票债券，即把息票债券看成一组零息票债券的组合，用现金流发生时点的即期利率贴现该现金流。因此，估计利率期限结构的核心是从息票债券信息中提取即期利率。

Anderson认为，对于宏观经济分析，简约的NS模型就能满足要求。本文采用NS模型估计即期利率，其形式如下：

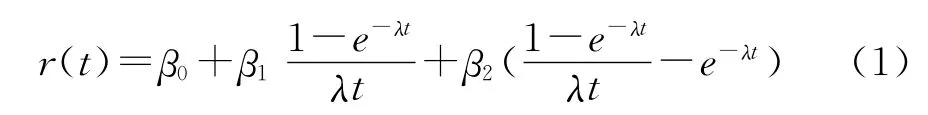
其中，r（t）表示t时刻的即期利率，β0、β1、β2、λ 是待估参数。β0、β1、β2分别是收益率曲线的水平、斜率和曲率因素，代表利率的长期、短期和中期水平，λ表示斜率和曲率因素负载的收敛速度。上述各参数的经验范围是［16］：β0+β1＞0，0．03＜β0＜0．1，-0.1＜β1，β2＜0．1，λ∈（0，1）。

对于NS模型的参数估计，一般采用的目标函数是最小化国债的价格误差，然而目标函数的选择应该由不同经济主体特定的目的决定。宏观经济政策制定者更关心的是货币政策的政策效应，收益率误差作为目标函数包含更直接的未来信息；而对于一般的市场投资者，由于债券的买卖差价包含更多的即期信息，债券价格误差作为目标函数更符合市场投资者的需要。另外，从直观感受上来说，选择收益率误差在问题的描述和参数的估计上更为直观和直接。Svensson曾指出，最小化价格误差会导致较大的短期债券收益率误差，而最小化收益率误差才能更好地拟合短期债券。为分析利率期限结构包含的宏观经济信息，本文直接对到期收益率进行拟合。另外，为消除最小化过程的时间效应，借鉴Kanjilal的思想［17］，采用修正久期的倒数对不同期限的国债到期收益率误差进行加权调整。此时，目标函数变为：

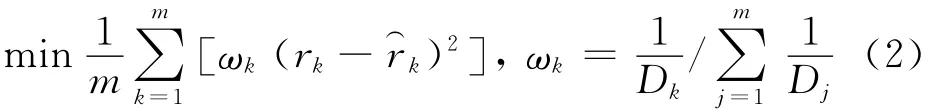
2.数据描述

本文数据来源于国泰安数据库和和讯债券网。考虑到数据的丰富程度，选取2001年11月～2013年4月的上海证券交易所的月度国债交易数据，即每个月最后一个交易日共计138个交易日的数据作为模型估计样本。上海证券交易所国债交易数据的主要缺陷是：一是国债种类较少。样本期内交易的国债共70支，导致样本数据较少；二是短期国债和长期国债较少。1年以下和10年以上的国债只占交易国债总数的17.14%；三是国债交易流动性不足。部分国债成交量很少甚至出现零交易，导致其价格形成机制低效。特别需要注意的是，奇异点的剔除，即将到期收益率低于同期活期存款利率的国债数据视为异常点予以剔除。由于债券刚发行上市交易或即将到期兑付，可能会导致流动性异常，因此将上市时间不超过1个月和剩余期限不足3个月的债券数据剔除。另外，由于参数模型对长期数据拟合效果不太理想，因而将期限为10年以上的债券数据剔除，用剩下的总计1837个样本点估计收益率曲线。

3.即期利率估计方法

通过最小化加权到期收益率误差估计即期利率，其过程需要算出债券在每个交易日的理论价格，再通过理论价格计算出债券的理论到期收益率。具有n次现金流，第i次现金流为Ci的息票债券的理论价格是

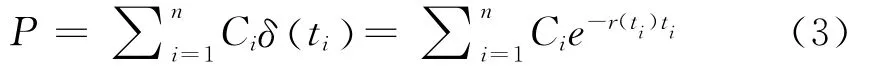
其中，δ是贴现函数，r是NS模型的即期利率。即期利率拟合流程为：首先在NS模型参数的经验范围内选取一定数量的初始值代入即期利率函数（1）式，然后通过理论价格（3）式计算出一组理论价格和理论到期收益率，连同实际到期收益率代入目标函数（2）式，最后求出取得函数最小值的参数组，否则过程循环直至得到全局最小值对应的一组参数值。本文用Matlab编程，采用遗传算法估计即期利率参数，由此可以计算出任一期限零息票债券在持有期间任意时刻的到期收益率。

4.收益率曲线估计结果

根据NS模型估计的即期利率的基本统计结果可知：年度平均即期利率基本呈现单调递增趋势，反映中国经济处于平稳较快增长阶段，2012年的即期利率最高，与该年的通胀水平最高的实际相符；即期利率的波动情况基本呈现两头高中间低的“U”型，反映短期和长期利率的波动较大，而两者容易分别受到货币政策和通胀的冲击，这在一定程度上表明了中国货币政策的跳跃性和较高的通胀水平。特别是近几年的长期利率波动剧烈，反映金融危机后中国面临着较大的通胀压力。

二、收益率曲线变动的主成分分析

1.收益率曲线移动的潜在因素分析

利率期限结构与宏观经济因素联系紧密，收益率曲线的移动可能来源于多个系统性或者非确定性的内、外部经济因素，如贷款的供给和需求、失业、通胀、经济周期、货币政策、市场参与者的活动等，在确定这些经济变量和债券价格的本质关系之前，核心的问题是需要理清哪些是影响收益率曲线移动方式的主要因素。相关的研究有Vasicek、Cox、Ingersoll和Ross的单因素模型，Longstaff、Schwartz和Gultekin、Rogalski的多因素模型，以及Heath的无套利模型。Duffee用因素分析法获得引起利率期限结构移动的潜在因素。Knez等研究发现，四因素模型能解释不同的货币市场工具价格变化的可能来源。Bliss应用因素模型分析不同期限的美国国债的价格和股票收益的变动情况，证明Litterman和Scheinkman用三因素分解利率曲线变化的结果是稳健的。在国内，朱世武与陈健恒基于SV模型拟合所得的收益率曲线，采用主成分分析法获得收益率曲线移动的三大潜在因素——水平因素、斜率因素和曲率因素，它们分别能解释收益率曲线变动的52.47%，29.71%及12.18%［18］。在一般文献中，由于关注点是利率变动的主要影响因素及各因素的作用大小，没有考虑宏观经济因素本身的变化程度对收益率曲线变动解释程度变化将导致微观经济主体利率风险管理工具发生变化。实际上，尽管影响利率变动的潜在因素的主成分没有变化，但不同时期影响利率变动的主成分结构可能大不相同。2008年美国金融危机后，美国量化宽松的货币政策导致全球通货膨胀对中国的传导及中国外汇储备急剧增加导致的广义货币大幅度增加、通货膨胀加剧会对影响收益率曲线移动的潜在因素结构产生的影响，即导致了利率曲线的水平、斜率和曲率因素解释曲线移动的比例发生变化，这可能会导致固定收益证券组合投资者或商业银行对风险管理工具的错误选择。因此本文运用主成分分析法，分金融危机前后两个时段提取收益率曲线变动的潜在因素。

2.主成分分析法：提取潜在因素

在对收益率曲线移动的潜在因素研究中，由于即期利率是期限的连续函数，因此可以选择一些特定的期限，那么相对应的即期利率就为主干利率，其变化就是原始变量，而主成分可表示为这些原始变量的线性组合，即：

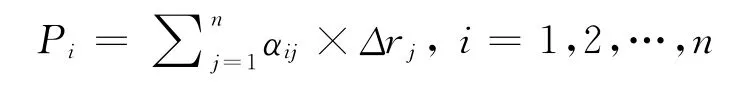
其中，Pi是第i个主成分，Δrj是第j个主干利率的变化值，αij则是相应的主成分系数。可根据国债市场的国债交易数据求解主成分的系数矩阵。步骤是：（1）选取一定数目的主干利率，按一定间隔（如一周、一个月）进行差分，计算出各自变化量，得到主干利率的变化矩阵M；（2）进一步求得变化矩阵的协方差矩阵征值λi和相应的特征向量 ［αi1αi2… αin］T，特征向量构成的矩阵就是系数矩阵。主干利率的联合波动体现为收益率曲线上的整体波动性，数量上等于而第i个主成分对整体波动性的解释能力（解释比例）为提供收益率曲线移动方式的重要信息，用来判断精确描述收益率曲线的移动需要的主成分个数。

3.2001年11月～2007年12月收益率月度变化的潜在影响因素

为提取2001年11月～2007年12月的利率变动的潜在影响因素（主成分），选择期限为3个月、6个月、1年、3年、5年、7年、10年的零息票债券的到期收益率为利率主干点，通过前文估计的每个月的利率期限结构，计算出这7个利率主干点的74个历史变化数据，按月差分得到主干利率的变化矩阵，进行主成分分析。主成分的计算结果显示，前3个主成分解释了99%以上的利率变动。主成分的解释比例如图1所示。

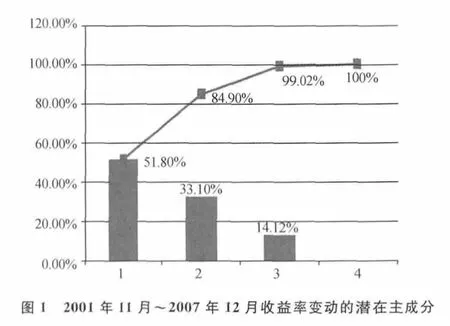
第一个主成分（相关的宏观经济变量是通胀即长期利率影响）解释利率变动的51.80%，第二个主成分（相关的宏观经济变量是产出即短期利率影响）解释利率变化的33.1%，第三主成分（相关的是货币政策等因素即中期利率影响）解释利率变动的14.12%。

由于前3个主成分的解释比例足够高，因此用前3个主成分能充分解释利率的变动。前3个主成分的系数如图2所示。

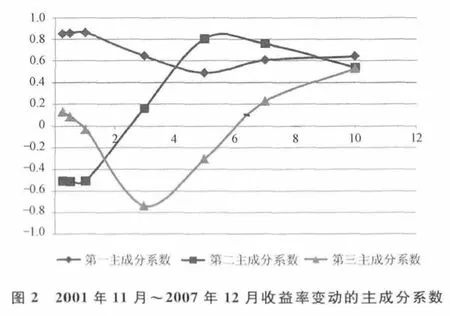
从图2可以看出，第一个主成分各个期限的系数都大于0，且除短期外近似于水平曲线。这一主成分解释了中长期利率的上下平移，可看作是平行移动成分，简称水平因素。第二个主成分向上倾斜，说明长、短期利率反向变动，解释了利率曲线的斜率变化，可看作是倾斜移动成分，简称斜率因素。第三个主成分大体呈现一个“U”形，说明短期利率与长期利率同向变动，与中期利率变动方向相反。这个主成分解释了利率曲线的曲率变化，可看作曲率移动成分，简称曲率因素。因此，解释收益率曲线移动的前3个潜在因素：水平、斜率和曲率因素总共解释了99%以上的曲线变化。有研究文献表明，这3个因素分别与长期、短期和中期利率变化紧密相关［19］，表明本时段内收益率曲线（主要是水平和斜率因素的变化）依赖于利率的长期、短期和中期因素的变化而变化，这一发现证明了选择水平、斜率和曲率三因素NS模型描述利率期限结构的合理性。

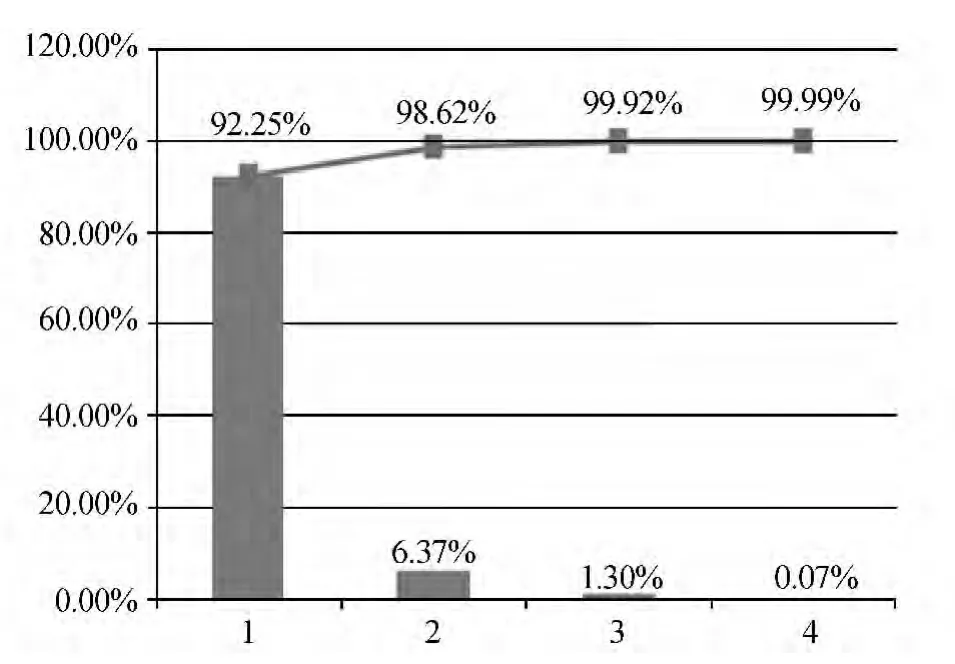
图3 2008年1月～2013年4月收益率变动的潜在主成分

4.2008年1月～2013年4月收益率月度变化的潜在影响因素

金融危机的爆发引起了全球性的经济衰退，截至目前它的影响还未消退。一方面，我国的经济增长很大程度上依赖于出口，金融危机迫使各国的进口需求锐减，造成我国经济的增速明显放缓；另一方面，美国为刺激经济，实行三轮量化宽松政策，带来全球性通胀问题，同时迫使人民币升值，人民币升值的预期导致大量资金流入使通胀压力上升，而全球经济衰退加剧了我国经济增长动力不足。考虑到通胀与收益率曲线的水平因素高度相关，产出缺口或经济周期与收益率曲线的斜率因素相关，这些主要经济变量的显著变化将对收益率曲线的形状和移动产生影响。为确定金融危机后利率变化的潜在因素，利用前文估计的月度NS利率期限结构，计算2008年1月～2013年4月的上述7个主干利率的64个历史变化数据，对按月差分所得的矩阵进行主成分分析。计算结果表明，前3个主成分依然解释了99%以上的利率变动。图3给出了前3个主成分解释利率变化的比例。根据图3，第一个主成分解释利率变动的92.25%，第二个主成分解释利率变化的6.37%，第三个主成分解释利率变动的1.3%。主成分的各期限系数见图4。如图4所示，第一个主成分各个期限的系数都大于0，且近似于水平曲线。这一主成分解释了利率的上下平行移动，为水平因素。第二个主成分向上倾斜，说明长、短期利率变动方向相反，解释了利率曲线的斜率变化，为斜率因素。第三个主成分大致呈“U”形，说明短期利率与长期利率同向变动，中期利率变动方向与之相反。这个主成分解释了利率曲线的曲率变化，为曲率因素。

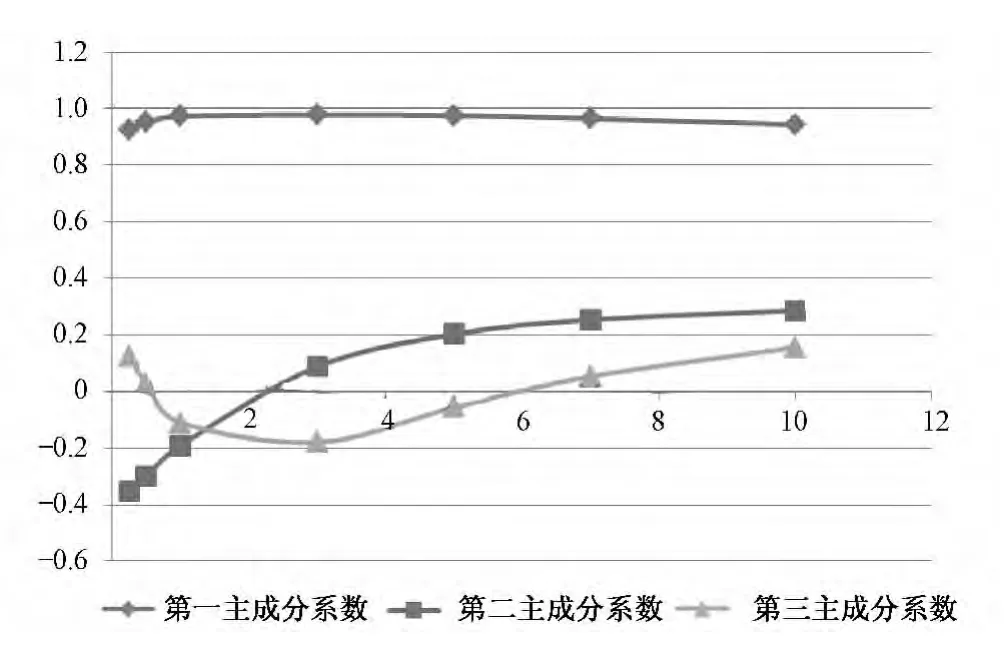
图4 2008年1月～2013年4月收益率变动的主成分系数

5.主成分分析结果说明及免疫工具选择

根据图1与图3可知，50%以上的收益率曲线移动依赖于水平因素（长期因素），而且前3个因素几乎代表着收益率曲线的全部变化，因而无论金融危机前还是金融危机后，影响收益率曲线变动的潜在因素相同。但对比图2与图4可以发现，危机前、后的收益率变化的潜在影响因素结构显著不同：金融危机前，水平因素仅能解释利率52%左右的变化，斜率和曲率也有重要影响；而危机发生后，水平因素的影响已经占据绝对主导，能解释利率92%以上的变化，斜率特别是曲率因素对收益率曲线移动的影响几乎可以忽略。换言之，危机前，收益率曲线经常发生非平行移动，而危机后，收益率曲线主要发生上下平行移动。

水平与通胀之间及斜率与增长之间的密切相关关系已得到了广泛验证。比如，Diebold等研究发现，水平和通胀之间、斜率和产能利用率之间的相关系数是0.4［5］。Kanjilal研究发现，水平和通胀及斜率和增长的相关系数是0.1～0.15，说明收益率曲线的主要移动方式可能代表着关键的宏观经济指标发生了变化，收益率曲线及其变化可以作为宏观经济运行的先头指标。根据前文分析，金融危机后，水平因素（长期因素）在收益率曲线移动中占据主导地位表明了经济的通胀压力越来越大，与我国实际情况相符。另外，由于固定收益证券投资者的目的在于为固定收益证券组合套期保值对冲利率风险，因而金融危机后长期或水平因素在收益率曲线移动中的主导地位对于这些投资者也具有重要启示：投资者在金融危机前、后应采用不同的风险免疫工具，危机前需要运用比较复杂的如久期向量或水平-斜率-曲率工具等，以对冲利率发生非平行移动产生的风险；危机后则只需使用传统的久期-凸性工具即可免疫投资组合的主要利率风险。

三、结论及建议

本文首先采用最小化的以修正久期倒数作为权数加权到期收益率误差为目标函数，估计NS模型的利率期限结构参数，根据即期利率的基本统计结果反映了我国主要的宏观经济事实，即经济处于平稳较快发展阶段，但金融危机后经受了较大的通货膨胀压力。然后通过对金融危机前和金融危机后两个时段的影响收益率曲线移动的潜在因素进行主成分分析发现：一方面，水平（长期利率）、斜率（短期利率）和曲率（中期利率）因素在金融危机前后均能解释收益率99%以上的变化，验证了三因素NS模型比较适合描述我国的国债收益率曲线；另一方面，收益率月度变化的潜在影响因素结构在危机前、后发生了显著变化，水平因素在金融危机后能解释收益率曲线移动的92%，而在金融危机前这一比例仅为52%，也就是说，收益率曲线的变动形式由危机前复杂的非平行移动变为危机后较简单的平行移动。最后说明这个结果对于国债市场投资的风险对冲策略和商业银行管理利率风险的工具选择有重要启示，并给出相应建议：在金融危机前需要采用比较复杂的久期向量或水平-斜率-曲率对冲工具免疫利率非平行移动的风险；在金融危机后只需要使用传统的久期-凸性工具，即可对冲利率平行移动的主要风险，实现较低成本与较高收益的平衡。

［1］NELSON C R，SIEGEL A F.Parsimonious modelling of yield curves［J］.Journal of Business，1987，60（4）：473-489.

［2］SVENSSON L E O.Estimating and Interpreting Forward Interest Rates：Sweden 1992-1994［EB／OL］.http：／／www.nber.org／papers／w4871，2013-09-25.

［3］梁艳，徐元华.基于不对称SV模型的隔夜信息对股市影响研究［J］.大连理工大学学报（社会科学版），2011，32（3）：34-38.

［4］Bank For International Settlements.Zero-coupon yield curves：technical documentation［EB／OL］.http：／／www.bis.org／publ／bppdf／bispap25.htm，2013-09-25.

［5］DIEBOLD F，GLENN D R，BORAGAN A S.The Macroeconomy and the Yield Curve：A Nonstructural Analysis［EB／OL］.http：／／papers.ssrn.com／sol3／papers.cfm？abstract＿id=473141，2003-10-21.

［6］WU T.Macro factors and affine the term structure of interest rates［J］.Journal of Money，Credit and Banking，2006，38（7）：1847-1875.

［7］ORPANIDES A，WEI M.Evolving macroeconomic perceptions and the term structure of interest rates［J］.Journal of Economic Dynamics and Control，2012，36（2）：239-254.

［8］HÖRDAHL P，TRISTANI O，VESTIN D.A joint econometric model of macroeconomic and term-structure dynamics［J］.Journal of Econometrics，2006，131（1-2）：405-444.

［9］RUDEBUSCH G D，WU T.A macro-finance model of the term structure，monetary policy and the economy［J］.The Economic Journal，2008，118（530）：906-926.

［10］王志强，贺畅达.时变货币政策规则对利率期限结构的动态影响分析［J］.宏观经济研究，2012，（10）：21-29.

［11］WILLNER R.A new tool for portfolio managers：level，slope，and curvature durations［J］.The Journal of Fixed Income，1996，6（1）：48-59.

［12］BRAVO J M V，Da SILVA C M P.Immunization Using a Parametric Model of the Term Structure［EB／OL］.http：／／www.rdpc.uevora.pt／handle／10174／8422，2013-09-25.

［13］DIEBOLD F X，JI L，LI C.A Three-Factor Yield Curve Model Non-Affine Structure，Systermatic Risk Sources，and Generalized Duration［EB／OL］.http：／／ssrn.com／abstract=910218，2004-03-09.

［14］余文龙，王安兴.基于动态Nelson-Siegel模型的国债管理策略分析［J］.经济学，2010，9（4）：1403-1426.

［15］刘艳萍，巩玉芳，迟国泰.基于利率非平行移动风险控制的资产负债组合优化模型［J］.管理学报，2009，6（9）：1215-1225.

［16］唐革榕.我国利率期限结构的静态拟合实证研究［D］.厦门：厦门大学，2006.

［17］KANJILAL K.Factors causing movements of yield curve in India［J］.Economic Modelling，2013，31：739-751.

［18］朱世武，陈健恒.交易所国债利率期限结构实证研究［J］.金融研究，2003，（10）：63-73.

［19］DIEBOLD F X，LI C L.Forecasting the term structure of government bond yields［J］.Journal of Econometrics，2006，130（2）：337-364.