基于储能系统提高风电外送能力的经济性研究

杨玉龙，李军徽，朱星旭

（东北电力大学电气工程学院，吉林 吉林 132012）

可再生能源大规模的开发与利用是保障我国能源安全、优化一次能源结构、发展低碳经济的重要途径，尤其是风力发电已经成为发展最快、技术最成熟、商业化前景最好的清洁能源开发方式之一。我国地域广阔，风能资源丰富，随着我国风电场规模的不断扩大和风电装机容量的快速增加，风电接入对电网安全稳定运行的影响日益凸显。我国风电多集中接入东北、华北、西北及内蒙电网末端，这些地区电网结构相对薄弱，跨区输送能力及协调能力不足。2009年以来，由于甘肃、黑龙江、内蒙古、吉林等风电大省（自治区）外送通道不畅，本地风电消纳能力不足，随着风电开发规模的扩大，风电窝电的波及范围扩大，其严重程度也随之增强。2011年，上述4个省（自治区）限电的比例都接近或超过了20%。近5年来风电连续爆炸式发展，其装机容量占电网最小负荷的比例逐渐提高，风电并网引起的弃风问题越来越严重，特别是“弃风限电”问题一度成为各方关注的焦点。

风电弃风限电的主要原因有调峰能力和输电容量不足，其中输电容量不足在一定程度上加剧了调峰的困难，也是导致风电弃风的一个不可忽略的因素。由于新增风电场的迅速增加，部分地区输电配套设施并不是很完善，这就使风电在输送过程中存在一定的限制，并且有的区域只是增加了少数风电场，没有必要为此而新建输电线路。

实践运行结果表明，大部分风电场等效为满发年用小时数大约在1900 h左右，风电能量密度较低。在现有的线路下，风电整体出力部分时段因输电容量的不足，导致风能不能全部输送出去，因此如何将因阻塞弃风电量合理地输送出去是急需解决的问题。储能系统（energy storage system，ESS）可以实现能量的时空平移，利用储能充放电使系统满足有功平衡，部分储能设备由于其具有响应速度快、单体体积小、安装使用便捷等优点，已在许多国家的示范工程中得到广泛应用，尤其是在风电场的应用，因此采用储能技术是比较有效的途径。

就此问题，目前有少数研究者从风电出力不确定性对输电容量规划问题做过初步研究。Billinton等[1]结合输电网设备、风电机组的可靠性以及风速的特性，对含有大型风电场电网的扩展规划提出了可靠性的评估方法，是该领域相对早期的研究；于晗等[2-3]将解析的概率潮流计算方法与Monte Carlo方法相结合，有效处理输电规划中的不确定性问题，是传统的确定性输电规划模型向不确定领域的延伸；文献[4-12]详细介绍了超级电容器储能和钒液流储能在风电中的应用，包括对其建模、制订控制策略及储能容量计算等，其工作重点放在了储能控制策略的制订来削弱风电的波动性及不可控性上，但没有考虑风电并网的输电问题，缺乏利用储能提高输电能力的研究。

由以上分析可知，利用电池储能系统能够实现能量时空平移，减少风电场弃风量。然而现今储能系统价格十分昂贵，对于给定的输电线路是否有必要配置储能设备以及如何配置储能容量可使其全寿命周期内效益最大是一个亟需研究的问题。

基于上述问题，为了降低因输电容量不足导致弃风所造成的损失，本文分析了影响输电容量的因素，提出了利用储能系统提高风电外送能力的方案，综合考虑了风电的输送需求、输电工程成本、输电运行效益、储能投资成本和储能运行成本，构建基于储能系统的输电线路的数学模型，利用储能系统平抑风电出力，在输电线路容量不足时存储受限弃风电量，在输电容量充裕时进行合理释放，使输电容量在输电线路要求范围以内，充分发挥已有输电线路的作用，达到合理弃风的目标，提高风电的接纳能力，以实现输电工程和储能系统整体效益的最大化。针对某省大型风电基地，利用本文提出的模型及方法对风电场配备储能系统受限情况加以改善，设计算例并运用算例结果验证所建模型及方法的合理性。

1 输电容量影响因素及风电场协议送电功率分析

输电线路传输容量是指输送功率距离的远近以及大小，影响输电容量大小的因素为负荷波动、线路参数和系统备用容量以及系统机组常规机组出力。

1.1 负荷波动

输电的目的是满足负荷的要求，负荷的波动性导致不同时段负荷的需求是不同的，线路输出的功率需在一定范围内，并且满足负荷波动的要求。

1.2 线路参数

输电距离和输电容量为电力输电线路的输电能力，其取决于线路的电压、允许的压降、导线型号等。对于不同的输电需求会选取不同输电能力的线路。

1.3 备用容量

电力系统在正常运行情况下，除去发电负荷所必需的容量外，为保证可靠供电和良好的电能质量，需保留一定量的额外系统电源容量，这部分容量称为系统的备用容量。系统备用容量的多少影响输电容量的大小。

1.4 机组常规出力

系统负荷存在一定的规律性和波动性，为保证电网系统的安全可靠运行，不可轻易启停机组。启停机组对系统经济性影响较大，因此不同的火电机组有常规的最小出力要求。

由于负荷的约束，所以输电通道的曲线由受电和送电双方根据电源调节特性和系统受端负荷特性协调确定。风电场输电线路的输电通道外送功率按如下公式确定[13]

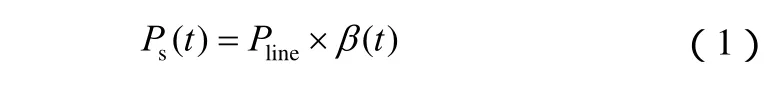
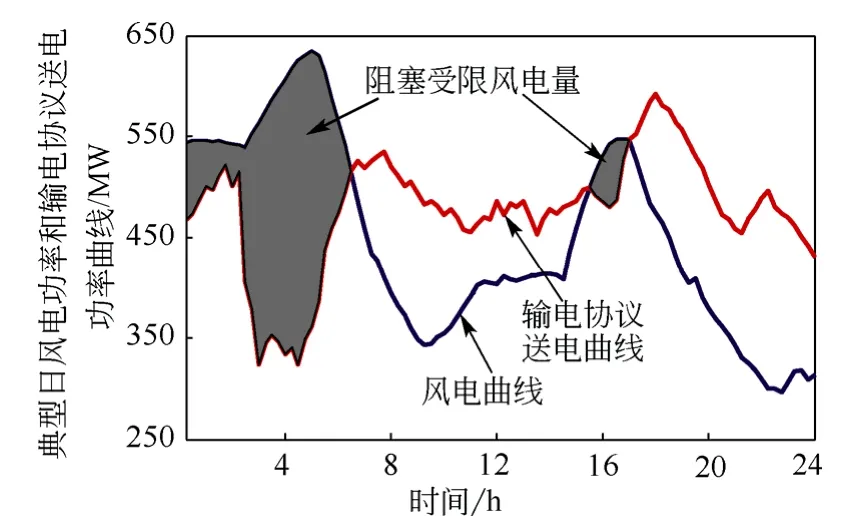
图1 典型日风电场功率与输电线路协议送电功率曲线图Fig.1 Schematic of typical day wind power and wind transmission agreement power

式中，Ps(t)为 t时刻输电线路协议输电功率；Pline为输电通道容量；β(t)为t时刻协议输电功率与输电通道容量的比值。

由图1可知，在协议输电功率小于风电场发出功率时，因阻塞而不能接纳风电，导致阻塞弃风；当协议送电功率大于风电场可发功率时，可能存在充裕接纳风电电量的空间，此时可通过储能的时空能量转换在输电线路协议送电功率不足时存储受限弃风电量，在输电协议送电功率充裕时进行合理释放，使输电容量在输电线路要求范围以内，并且获得最大的效益。

2 基于ESS的输电线路数学模型及经济特性分析

本工作综合考虑了风电的输送需求、输电工程成本、可能阻塞弃风损失、输电运行效益以及储能投资成本等因素，构建了能够反映输电工程和储能的综合收益的目标函数，即

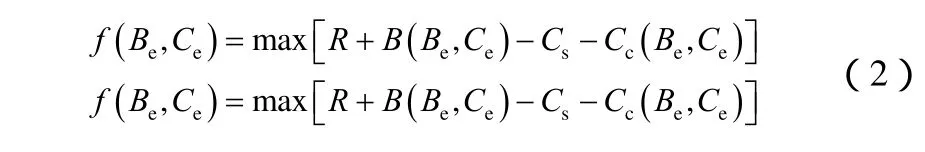
式中，f为风电外送输电工程和储能全寿命周期的综合收益；R为电网输电工程收益；Cs为输电工程成本；Cc为储能系统投资成本；B为利用储能系统减少阻塞弃风所获得的收益，定义为储能系统收益；Be为储能配置的容量；Ce为储能配置的功率。

满足式(2)的Be和Ce即为综合收益最优的储能容量和功率。

电网的输电工程收益R正比于储能提高的风电量和风电基地原发电总量之和，其计算公式为

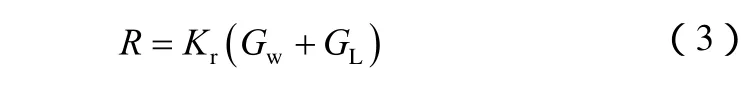
式中，Kr为输电企业外送单位风电电量的价格；Gw为输电工程每年送出的风力发电电量；GL为ESS提高的风电输电电量，计算公式为

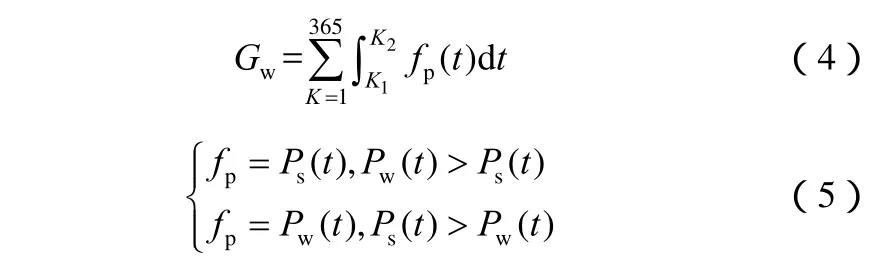
式中，Pw(t)为风电基地实际功率曲线；fp(t)为可送出风电功率曲线。

储能系统收益 B(Be,Ce) 正比于储能寿命期限内提高的风电接纳电量，其计算公式为

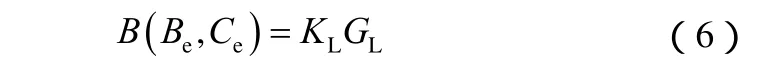
式中，KL为电网因输电容量不足造成弃风损失的补偿单价，其求法为

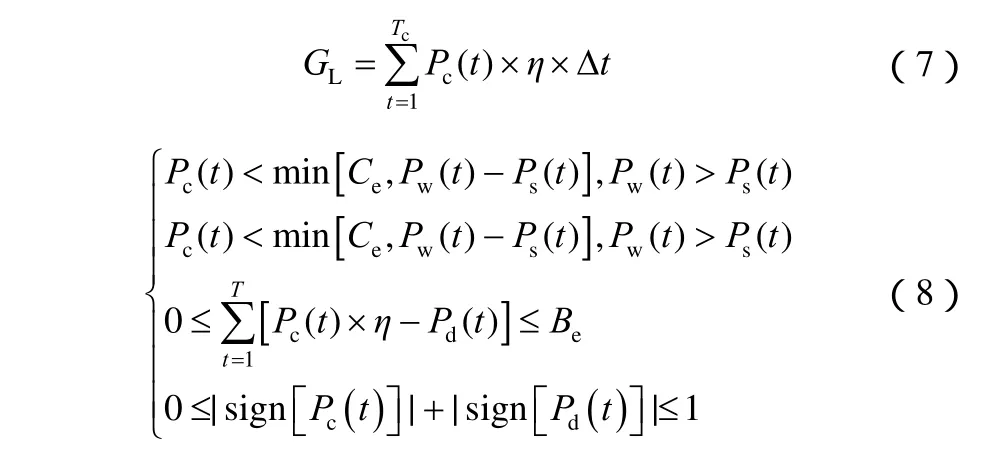
式中，Tc为储能寿命周期；Pd为储能放电功率，MW；Pc为储能充电功率，MW；η为储能能量转换效率；sign为符号函数。

输电工程建设投资成本Cs（按静态回收考虑）的计算公式为

式中，L为输电距离；Ks为单位容量、单位长度下的输电工程造价；Ts为输电工程投资静态回收期。

储能系统投资成本Cc的计算公式为

式中，C1为储能系统容量价格；C2为储能系统功率价格。

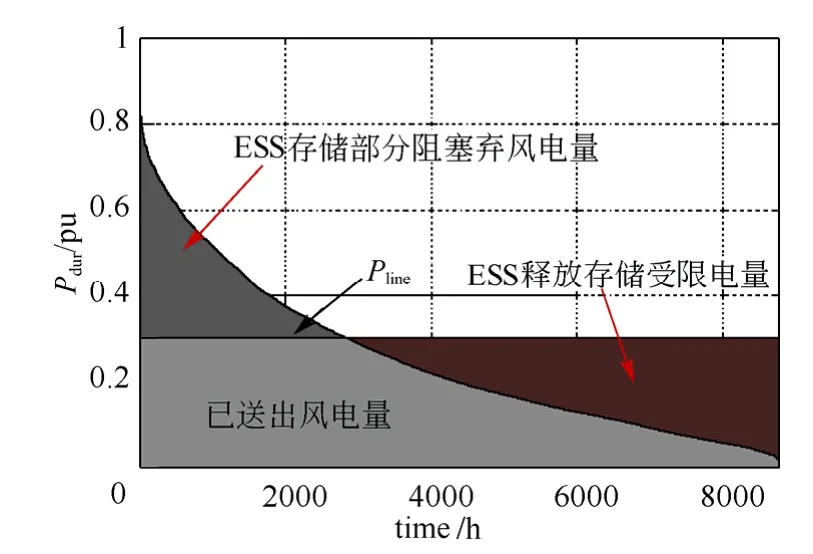
图2 风电外送储能系统作用示意图Fig.2 Schematic of the wind transmission capacity with ESS

由图2可知，在已知风电场持续出力特性和风电外送输电容量水平的前提下，若确定了储能系统配置的容量，则可计算出可以送出的风电量和其相应的风电弃风损失电量。由此可知，提高Be和Ce可更好地减少弃风的损失，但需增加储能系统的投资；降低Be和 Ce可减小储能系统投资成本，但不能保证发出的风电电量完全送出，此时由于弃风损失增加，因此存在一个 Be和 Ce使得风电外送的储能和输电工程整体收益最大。

3 算例分析

3.1 算例条件

以某省某大型风电基地外送输电工程容量优化为例，此省涡风情况比较严重，风电外送比较大，输电容量不足而导致弃风情况严重，在储能寿命期限内，输电线路容量不变，此算例分析并未考虑资金的时间价值，给定算例条件如下。

（1） 输送电企业单位风电量的外送价格Kr=0.06元/(kW·h)。

（2）输电工程单位综合造价Ks=100万元/(MW/100 km)。

（3）输电通道容量Pline=750 MW，输电线路长度L=200 km。

（4）输电投资静态回收期Ts=20 a。

（5）电网因输电容量不足而阻塞弃风损失补偿单价 KL=0.6 元/(kW·h)。

（6）储能系统采用容量、功率可独立配置的钒液流电池储能系统，其使用寿命为 10 a，循环使用次数大于12000次，系统能量效率η为90%，容量价格C1为900元/(kW·h)，功率价格C2为3600元/kW，目前价格比此价格要高一些；其运行对环境污染较小，暂不计处理污染的费用。

（7）考虑输电通道的实际利用效率和受端系统的负荷特性，拟订协议送电曲线为：受端系统负荷低谷时段（3:00～5:00）β(t)为0.5，在此段时间通常是风力发电高发时段，导致部分风电量不能及时送出；高峰负荷时段（17:00～18:00）β(t)为1，此时却是风力发电的低发时段，负荷端却急需电量，腰荷时段的β(t)为 0.83。

3.2 算例结果

根据式(7)，能够计算出配置不同储能对输电线路限电的改善效果，随着储能系统配置逐渐增加，其减小的限电量随之增加；伴随储能系统配置的不断增加，到达一定程度时，此风电场群的输电受限情况能够全部得到改善，但过多的配置并不能保证取得最佳收益。

由式(2)计算得：基于输电受限程度，首年储能最优配置功率为46 MW、首年最优配置容量为428 MW·h时，可提高因输电年受限限电量106 GW·h（图3），占年总限电量的8.4%；其年综合最大效益达到1.7089亿元。

图3 配置ESS前后此风电基地年限电量累计图Fig.3 The wind power annual abandoned duration curve before and after configure the ESS

3.2.1 储能系统寿命期限内配置及效益的动态分析

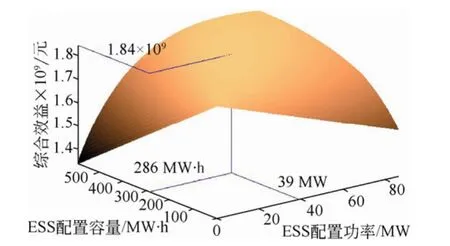
图4 不同ESS的配置情况与综合效益对应图Fig.4 Comprehensive benefits with different configurations of ESS

随着每年风机装机容量的不断增大，在给定输电线路容量情况下，未来10年其所配置的储能系统功率和容量也必然发生变化，由图4可知，当储能系统功率及容量配置较小时，随着配置功率和容量相应增加，综合效益增大；当储能配置功率及容量超过某值时，其综合效益将随其配置增加而减小。由式(2)计算可得：在此输电线路受限情况下，储能最优配置功率为39 MW、最优配置容量为286 MW·h时，可提高因输电总受限限电量783.6 GW·h；其综合最大效益达到 18.403亿元。储能投资收益率为10.38%，输电投资收益率为23.26%，虽然储能的投资收益率小于输电的收益率，但其可能带来的收益也是可观的。

由图5可知，随着年限的推移，储能系统带来的收益呈先增加，到第四年后开始减少的趋势。由此可知其原因为随着风机装机容量的增加，储能配置需求不断增加，但当风机装机容量到达一定程度，大部分可发功率大于协议送电功率时，可输电空间减少，储能配置需求减少，这不仅导致整体经济性降低，而且导致了部分储能配置闲置的情况，降低储能效率。由此可知，可在后几年相应扩建线路，使储能起到延缓线路建设的作用。

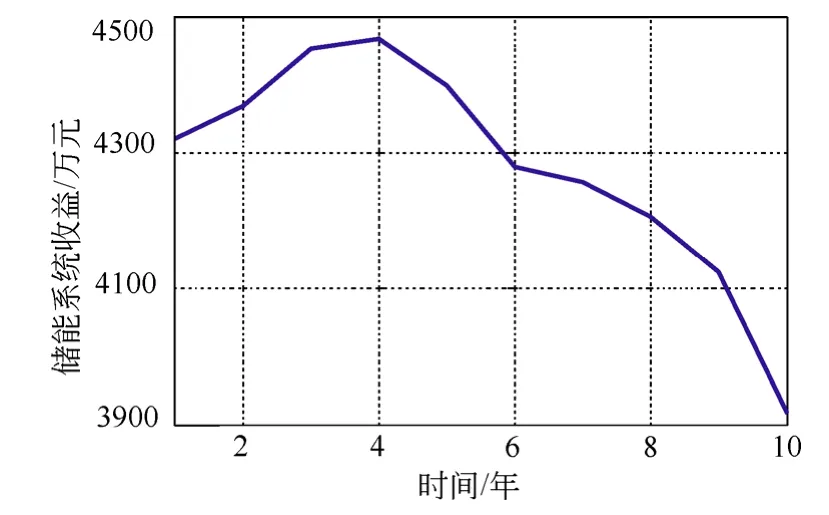
图5 ESS寿命期限内ESS收益曲线图Fig.5 ESS benefits curve within ESS lifetime

3.2.2 储能系统价格对最优配置及最大综合效益影响分析

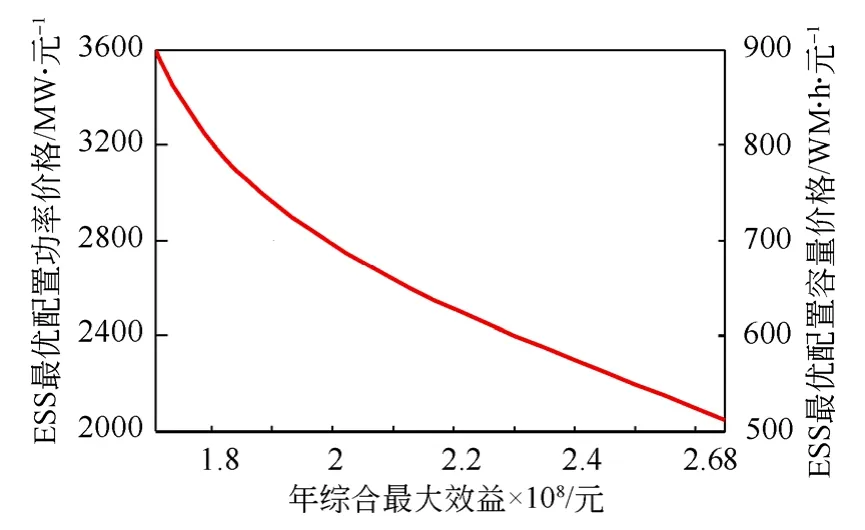
图6 ESS最优配置不同价格下年最大效益曲线图Fig.6 Maximum benefits curve of optimal configuration with different ESS prices

此处分析了储能系统价格对最优配置及综合最大效益的影响，由图6和表1可知，在当前储能系统价格下，以首年为例，其综合最大效益并不显著，但随着储能系统价格的逐步下降，其最优配置及综合最大效益随之增加，经济效益愈发显著，由此可知储能系统价格昂贵是影响其大规模应用的主要原因。

4 结 论

提出了利用储能系统容量的配置提高输电外送能力的方案，通过实际算例分析得到主要结论如下。

（1）分析了影响输电容量大小的因素有负荷波动、线路参数和系统备用容量以及系统机组常规机组出力，并给出了风电场协议送电功率的确定公式。

（2）提出了利用储能系统提高风电外送能力的优化方法和建立基于储能的输电线路效益评估模型，综合考虑了风电的输送需求、输电工程成本、输电运行效益、储能投资成本以及可能的阻塞弃风损失等因素。

（3）对于给定算例条件下某省风电基地输电线路受限情况，利用储能系统提高其输电外送能力，其最优配置功率为 39 MW，最优配置容量为 286 MW·h，每年可减少风电场限电量 783.6 GW·h，综合收益18.403亿元。经过计算，虽然储能投资的收益率小于输电投资的收益率，但其收益也是不容忽视的。分析得出了在储能系统寿命期限内，随着风机装机容量每年不断增加，储能系统收益呈现先增后降的趋势。

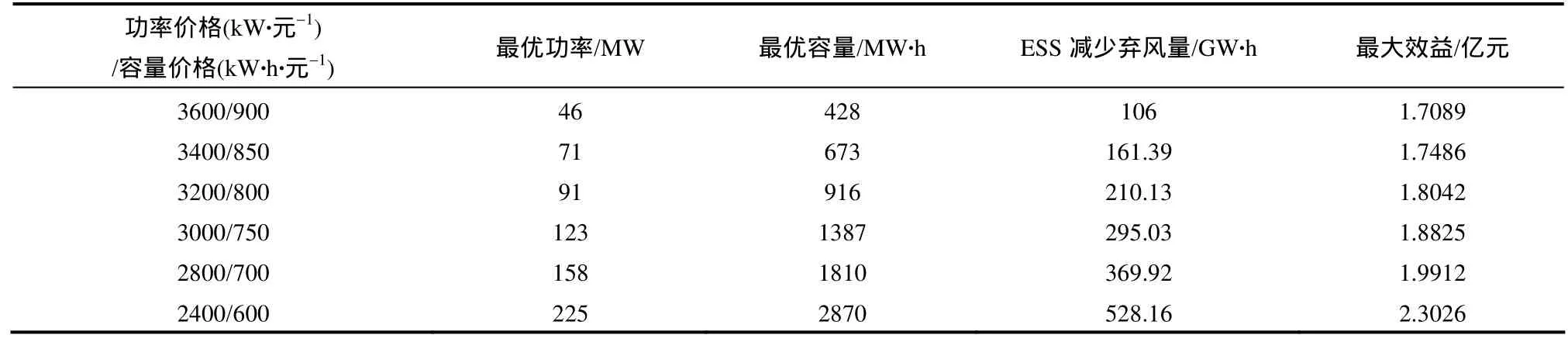
表1 ESS不同价格与最优配置、减少弃风量及效益对应表Table 1 Comparison with ESS different prices , optimal configuration , reduction of wind curtailed and benefits

（4）分析了储能价格对配置最优及最大效益的影响，随着科技的发展，储能系统价格必然降低，最优配置和最大效益都大幅度增加，对因阻塞弃风及收益改善效果明显。

[1] Billinton R，Wangdee W.Reliability-based transmission reinforcement planning associated with large-scale wind farms[J].IEEE Trans.on Power Systems，2007，22（1）：34-41.

[2] Yu Han（于晗），Zhong Zhiyong（钟志勇），Huang Jiebo（黄杰波），Zhang Jianhua（张建华）.A chance constrained transmission network expansion planning method associated with load and wind farm variations[J].Automation of Electric Power Systems（电力系统自动化），2009，33（2）：20-24.

[3] Yu H，Chung C Y，Wong K P，et al.A chance constrained transmission network expansion planning method with consideration of load and wind farm uncertainties[J].IEEE Transactions on Power Systems，2009，24（3）：1568-1576.

[4] Gao Ci wei（高赐威），He Ye（何叶）.Research of electric network planning with wind power integration considered[J].Journal of Electric Power Science and technology（电力科学与技术学报），2009，24（4）：19-24.

[5] Mu Gang（穆钢），Cui Yang（崔杨），Yan Gangui（严干贵）.A static optimization method to determine integrated power transmission capacity of clustering wind farms[J].Proceedings of the CSEE（中国电机工程学报），2011，31（1）：15-19.

[6] Ding Ming（丁明），Xu Ningzhou（徐宁舟），Bi Rui（毕锐）.Modeling of BESS for smoothing renewable energy output fluctuations[J].Automation of Electric Power Systems（电力系统自动化），2011，35（2）：66-71.

[7] Yu Peng（于芃），Zhou Wei（周玮），Sun Hui（孙辉），Guo Lei（郭磊），Sun Fushou（孙福寿），Sui Yongzheng（隋永正）.Hybrid energy storage system and control system design for wind power balancing[J].Proceedings of the CSEE（中国电机工程学报），2011，31（17）：127-133.

[8] Guo Xueying（郭学英），Zheng Jianyong（郑建勇），Mei Jun（梅军），Xu You（徐友）.Power conditioning and control system for grid connected wind farm based on super-capacitor energy storage[J].Renewable Energy Resources（可再生能源），2011，29（2）：28-32.

[9] Wang Zhenhao（王振浩），Liu Jinlong（刘金龙），Li Guoqing（李国庆），Xin Yechun（辛叶春），et al.Power and voltage regulation of wind farm based on EDLC energy storage[J].Electric Power Automation Equipment（电力自动化设备），2011，31（3）：113-116.

[10] Li Guojie（李国杰），Tang Zhiwei（唐志伟），Nie Hongzhan（聂宏展），Tan Jing（潭靖）.Modelling and controlling of vanadium redox flow battery to smooth wind power fluctuations[J].Power System Protection and Control（电力系统保护与控制），2010，38（22）：115-119.

[11] Li Xiao（李霄），Hu Changsheng（胡长生），Liu Changjin（刘昌金），Xu Dehong（徐德鸿）.Modelling and controlling of SCES based wind farm power regulation system[J].Electric Power Automation Equipment（电力系统自动化），2009，33（9）：86-90.

[12] Jin Wentao（靳文涛），Li Bei（李蓓），Xie Zhijia（谢志佳）.An analysis for the need of a battery energy storage system in tracking wind power Schedule output[J].Energy Storage Science and Technology（储能科学与技术），2013，2（3）：294-299.

[13] Hou Tingting（侯婷婷），Lou Suhua（娄素华），Zhang Zihua（张滋华），Wu Yaowu（吴耀武）.Capacity optimization of corollary thermal sources transmitted with large-scale clustering wind power[J].Transactions of China Electrotechnical Society（电工技术学报），2012（10）：255-261.