波纹管驱动超精密定位平台建模及复合控制
田艳兵, 王涛, 王美玲, 张栋
(1.北京理工大学 自动化学院,北京 100083;2.青岛理工大学自动化工程学院,山东青岛 266520)
0 引言
精密伺服是超精密加工中的关键技术,是衡量一个国家超精密加工水平的重要指标。目前,国内外超精密伺服控制精度已经达到纳米级。精密伺服定位系统多以电驱动,为避免摩擦对控制效果的影响,一般装配有气浮导轨。电机驱动分为直接驱动和间接驱动两种模式。间接驱动借助滚轴丝杠等传动机构将电机转动转换为直线运动,其传动效率较低,往返行程间隙大,限制了控制精度的提高;直接驱动采用直线电机驱动[1],如音圈电机等[2],传动效率高,但是输出力较小。2007年,东京工业大学的H.Shino等采用8个音圈电机驱动[3],完成了5nm精度等级的二维精确定位,定位精度很高,行程受到限制。特别是对于二维定位多采用“H”型叠压结构,机械结构复杂。有学者尝试在一个平面机械结构内的二维定位,天津大学的冯晓梅等设计了基于音圈电机的气浮平台,精度能达到微米级[4]。
目前,气动伺服系统多采用气缸驱动,电磁干扰小,设备维护方便。近年来,气缸驱动或者气缸复合驱动的超精密定位系统在国内外得到广泛研究和运用,取得了一些成果。台湾科技大学的Mao-Hsiung Chiang等采用气缸和压电驱动结合的模式[5],较好的解决了控制精度和运动行程的问题,其控制精度达到微米级,但两级进给模式使得机械结构复杂,不利于控制精度的提高。
基于气缸的定位伺服系统精度不高,往往需要配备双级驱动机构,在二维定位中采用的“H”型结构后,使得机械平台更复杂,各种承载平台之间存在的摩擦不利于精密控制[6]。本文设计了一种基于新型金属波纹管驱动的单级进给模式的气动定位平台,以气浮平台为支撑,采用高精密光栅尺进行位移反馈,简化了系统机械结构,降低了成本。针对系统在运动过程中存在的迟滞现象,建立基于PI的迟滞数学模型,为了改善系统的控制效果,采用了PI逆模型控制和反馈PID自整定控制,在2 500 μm的行程范围内,取得了较好的控制精度和响应速度。
1 硬件平台
系统硬件主要由3部分组成。基于波纹管的运动驱动机构;气浮导轨产生的静压轴承支撑的工作平台以及位置检测反馈部分。由单片机调节高精度压力比例阀,控制波纹管内部压力,调整其伸缩量,控制平台位移。为增加平台刚度和稳定性,在运动平台另一侧安装有预紧弹簧。整个系统的结构框图和实物图如图1所示。

图1 系统结构框图和实物图Fig.1 Block diagram and actual picture of the system
1.1 运动驱动机构
系统驱动机构采用电气比例阀控制的驱动波纹管。波纹管是一类子午线呈波纹状的旋转体,依靠内部气体压力的变化产生伸缩运动,产生位移。按形状可分为“U”型、“Ω”型、“S”型等[7]。其中“U”型波纹管承受压力大,静态特性较好,输出位移与输入信号线性关系好,无摩擦,模型简单。通过单片机的12位D/A数据口控制高速比例阀,实现波纹管的位置控制[8]。
1.2 支撑体结构
支撑体结构主要由气浮导轨和工作平台组成,工作平台由高刚度的多孔质气浮导轨产生静压空气轴承支撑。
气浮导轨为工作台定向并提供无摩擦支撑。气浮导轨的气孔喷射压缩空气到工作台表面产生悬浮力,当悬浮力与工作平台重量平衡时,平台处于稳定悬浮状态。支撑台负载发生变化或有外界扰动时,气浮平台表面和载物台之间的间隙改变,悬浮力重新达到平衡[9],具有自平衡能力。该系统气浮导轨为封闭矩形,气浮导轨的上下、左右均有气孔。上下两侧气浮导轨会在上、下两个面产生静压面,以提高静压轴承的刚性,左、右两个面静压面起到导向作用。对于空气静压轴承设计可以采用有限元分析方[10-11],在此不再赘述,多孔质空气静压轴承的原理示意图如图2所示。

图2 气浮导轨Fig.2 Aerostatic slider
1.3 检测元件
系统采用MicroE公司生产的Mercury3500系列的光栅尺进行位置反馈,其检测分辨率可以达到5nm[12]。
2 系统迟滞模型
波纹管作为驱动机构,近年来已有学者对其进行了一定的研究,其工作寿命和机械特性已经在实验中得到验证[13]。作为执行机构,波纹管在低速或者静态下,有着很好的线性,但是其采用气体驱动,由于气体本身的可压缩性,在动态运动的情况下,波纹管驱动系统输入和输出之间存在迟滞现象。迟滞是指系统的运行轨迹在上行和下行之间存在间隙,也即系统的输入和输出之间并不是一一对应的关系,具体到波纹管来说,就是其电磁比例阀的输入电压所对应的波纹管产生的输出位移不是一一对应的,这对于超精密定位系统有着较大的影响。
目前关于波纹管的迟滞特性大多基于金属材料特性进行改进,来减小迟滞的影响,但是效果不好。本文对其迟滞特性进行研究,通过建立系统迟滞模型,找出针对性的控制策略,降低迟滞对系统定位精度的影响[14]。
系统迟滞特性由其初载曲线确定。在该系统中,其初载曲线可以通过实验获取,将驱动电磁压力比例阀从无源状态下开始,逐步施加驱动电压到最大值过程中,采集位移参数,得到波纹管驱动平台的运行轨迹。为了验证波纹管的迟滞特性,平台加载后,进行初载特性实验,其实验数据见表1。
波纹管驱动平台的初载特性实验在低频输入下进行,电压的变化速率较慢。实验中系统输入电压信号变化速率为0.5 V/s,系统的输出响应可以很好的抑制波纹管的动态特性,增加系统模型的精度。
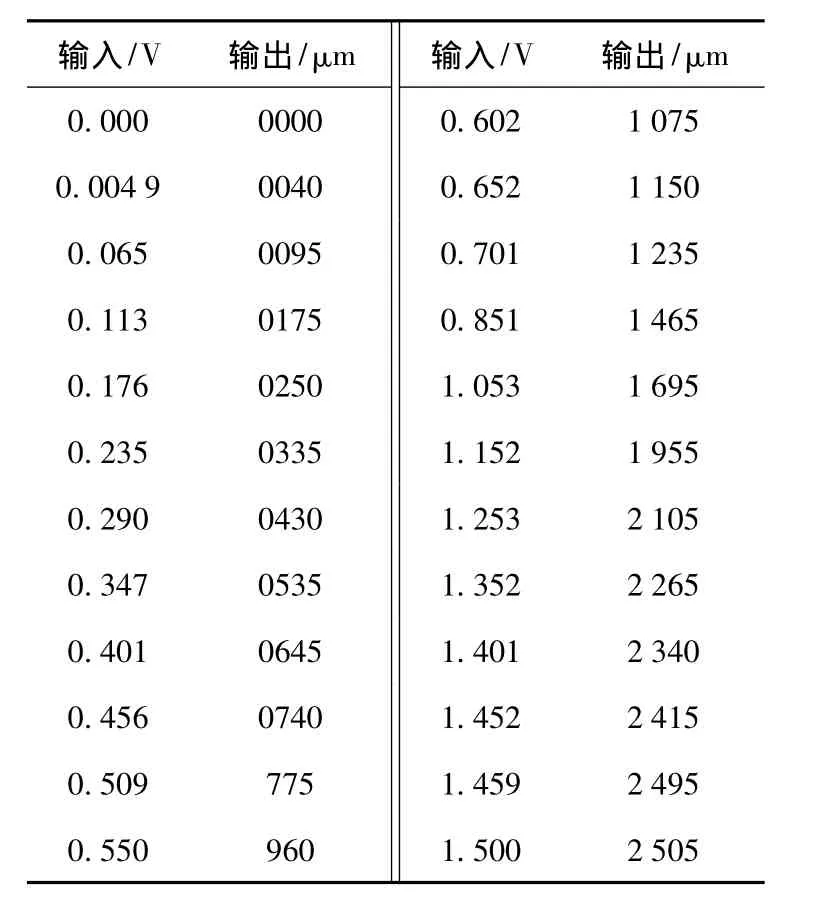
表1 实验数据Table 1 Experimental data
2.1 PI模型
从表1的实验数据中可以看出,波纹管驱动系统迟滞现象明显,需要建立针对性的迟滞模型。目前常见的迟滞模型有Preisach模型、KP模型、PI模型等。PI模型是从Preisach模型发展而来的一种模型[15],由Krasnosel’skii和Pokrovskii建立,由许多加权重叠的间隙算子(Backlash Operator)组成的,算子的特性由阈值r和权值ω决定,不同阈值的迟滞算子通过加权ω叠加,形成迟滞特性曲线。阈值r决定了基本迟滞算子的宽度,权值ω决定了基本迟滞算子的斜度[16]。
在构建迟滞模型时,间隙算子的数学形式为

其中,T为采样周期。式(1)是一个基于y(0)的递归公式,有
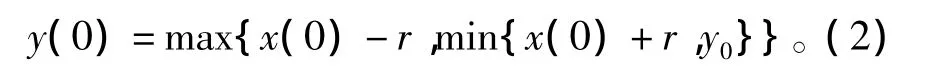
y0为系统在没有激励源的情况下的初值,一般情况下可以取0。
加权ω之后形成加权迟滞算子,即

从而PI迟滞模型可以通过n个加权迟滞算子累加得到,有
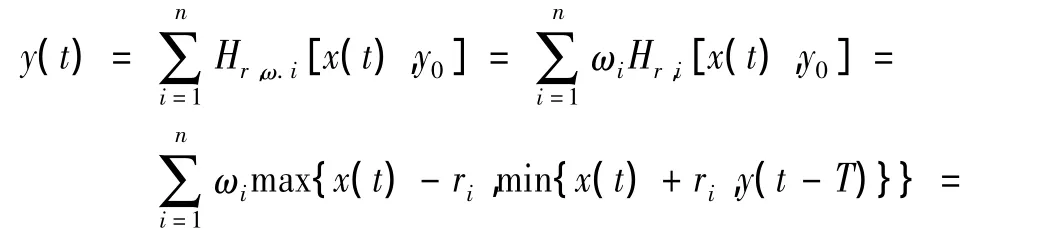
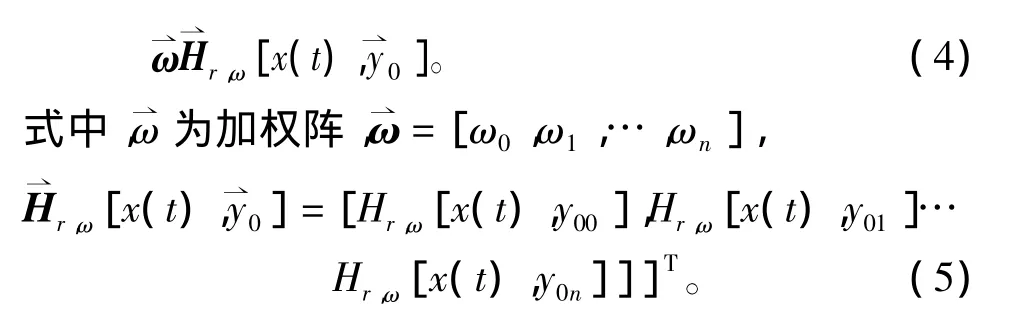
PI模型的一个显著优点是模型的解析逆容易得到,从而可以通过PI逆模型对控制对象线性化,线性化后的模型便于控制和分析,在线性化的基础上进行控制方案的研究,其线性化原理如图3所示[17]。
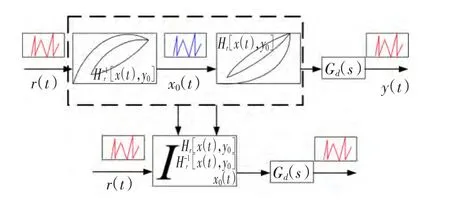
图3 基于PI逆矩阵的控制器设计原理Fig.3 Controller design based on PI inverse matrix
2.2 模型参数辨识
从式(4)可以看出,决定系统PI模型的2个主要参数为r和ω。在实际操作过程中,PI模型参数的辨识可以利用系统带载实验数据形成的初载曲线进行,根据实验数据,对式(5)所描述的数学模型,用Matlab的ployfit函数进行拟合,并用最小方差优化,可以得到辨识后的系统参数如表2所示。
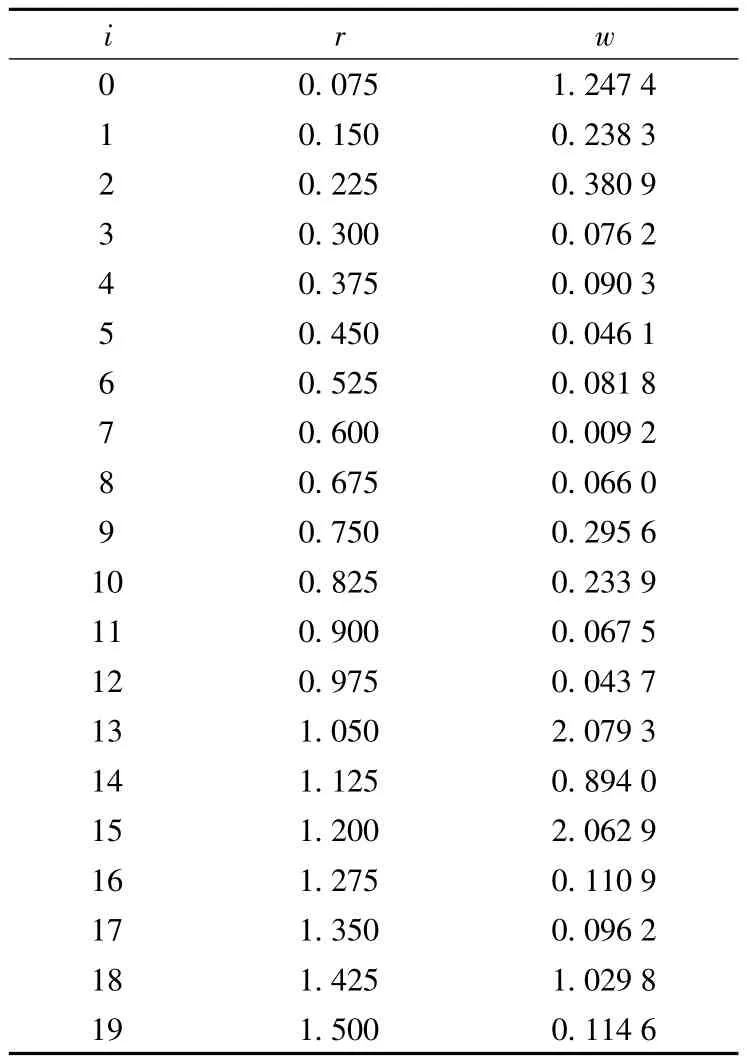
表2 参数辨识结果Table 2 Result of parameters identification
结合PI模型,其解析逆模型参数也容易求得,可以建立基于逆模型的前馈控制器,能够较好的完成轨迹跟踪。
2.3 模型验证
为了验证建立模型的精度,在实验室平台上进行实验[18]。仿真实验中将系统模型放在SIMULINK中进行,压力比例阀输入信号和压力输出按线性关系处理。而对于实验平台则是按照一定规律输入电压信号,通过光栅尺检测位移输出。上位机软件采用Labwindows进行设计,下位机采用MSP430单片机系统对高精度压力比例阀进行控制,调整压力,控制波纹管伸缩量,并和上位机进行通信。在实验中,电磁比例阀控制电压信号变化轨迹为(0.0v-1.5v-0.0v-1.4v-0.2v-1.0v-0.5v-0.8v-0.6v)。
变化速率为0.5V/s,实验输出和模型输出如图4所示。

图4 模型输出和实验输出Fig.4 Model output and experimental output
从图中可以看出,通过初载曲线拟合建立的PI迟滞模型可以很好地逼近系统的实际输出,所建立的迟滞模型是有效的,精度较高。
3 控制策略研究
实验表明,在波纹管驱动特性中,迟滞特性是影响其控制精度的主要因素,因此在控制器设计中,重点考虑迟滞特性的线性化,根据PI模型采用PI逆模型进行处理。
3.1 前馈开环控制
将波纹管驱动系统辨识得到的迟滞模型进行求逆,逆模型直接串联在被控对象前面,将系统线性化,逆模型作为前馈控制器。这种方案称为前馈控制方案,尽管缺少反馈环节,但是在某些精度要求不高的场所,该种方案可以减少位置检测反馈装置,从而从很大程度上降低成本。实验研究表明,采用直接前馈开环控制,控制精度可以达到十几个微米的等级,因此也有一定的实用价值。
考虑系统在运动过程中存在的动态特性影响,可以在前馈控制器前加入针对动态特性的控制环节,作为总的前馈控制器。波纹管驱动精密定位平台前馈控制框图如图5所示。

图5 系统迟滞逆模型开环控制Fig.5 Open-loop control based on inverse hysteresis model
3.2 基于PSO自整定的复合控制方案
为了进一步提高系统的控制精度,在定位系统中采用了前馈开环控制加反馈环节的控制方案。前馈控制用来校正波纹管驱动执行器的迟滞非线性,提高对参考位移信号的跟踪能力;反馈调节用来进一步校正前馈补偿没有消除的偏差以及由模型的不确定性带来的误差,从而弥补建模带来的定位误差,使得工作平台跟踪精度进一步提高[19]。
反馈环节采用数字PID控制,PID参数对于控制效果非常重要,但参数整定较为繁琐,且效果不一定最佳,特别是系统模型参数变化的情况下,PID参数需要针对不同情况进行整定。对于定位平台,由于其承载质量的不同,不同的PID参数会影响控制效果[20]。为了改善参数整定效果,考虑到运动控制系统调整周期短,在复合控制中,通过粒子群算法对PID参数进行优化,确定系统最优参数,可以将不同负载时的控制参数预先整定储存,以改善系统的实时性能,提高系统的控制精度。
粒子群算法(Particle Swarm Optimization,PSO)是遗传算法的一种,和遗传算法相似,它也是从一定范围内的随机解出发,通过迭代寻找最优解,通过适应度函数-fitness来评价辨识参数的品质,但它比遗传算法规则更为简单,它没有遗传算法的“交叉”(Crossover)和“变异”(Mutation)操作,主要是通过模拟鸟群寻找食物的过程,提出的优化算法[21]。该算法简单,编程较容易实现。PSO算法的关键在于适宜度函数的设计,根据运动控制系统的特点和控制效果,适宜度函数可以选择为

其中,W1,W2,W3,W4为权重函数,在寻优过程中,充分考虑运动定位控制的特点,对系统的稳态误差和调节时间作为2个主要衡量指标,权值分别取值为50,30,2,10。
对于该适宜度函数,采用PSO算法进行寻优[22],目的是使适宜度函数达到极小值。PID控制效果取决于3个参数Kp、Ki、Kd,因此训练的粒子维数为3,粒子数目取30个,最大迭代次数2 000次。PSO算法参数整定的具体实现步骤为:
1)系统初始化,设定Kp、Ki、Kd初值,确定Kp、Ki、Kd的范围,赋予粒子初始位置和速度以及pbest和gbest,确定系统的合法的Vmax和Xmax。
2)对每个粒子Kp、Ki、Kd阶跃响应,实验得到时域内的性能指标e(∞)、ts、tr和σ%。
3)根据阶跃响应参数,据式(6)计算种群中每个粒子适应度值。
4)对于每一个粒子,根据计算的适宜度函数,寻求更优值,确定是否更新其pbest和gbest值。
5)更新粒子的速度和位置。
6)判断粒子位置和速度的合法性。
7)如果达到最大迭代次数转至8),否则转至2)。
8)寻优结束,得到PSO寻优后PID的参数,即Kp、Ki、Kd。
PSO寻优的PID复合控制方案框图如图6所示。

图6 基于PSO的复合控制方案Fig.6 Compound control based on PSO
4 实验和分析
分别利用传统PID控制和自寻优PID复合控制方案控制,在波纹管驱动平台上进行实验,系统主要参数为
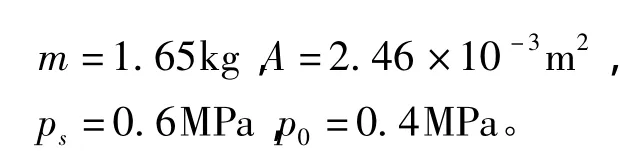
m为移动平台的自重和负重;A为波纹管有效受力面积;ps为气源压力;p0为静压轴承气源压力。
4.1 PID控制方案
对于传统的PID控制,进行实验研究,取Kp=0.46,Ki=0.06,Kd=0.01,其阶跃稳态误差为0.16 μm、超调量为3.7%,如图7所示。
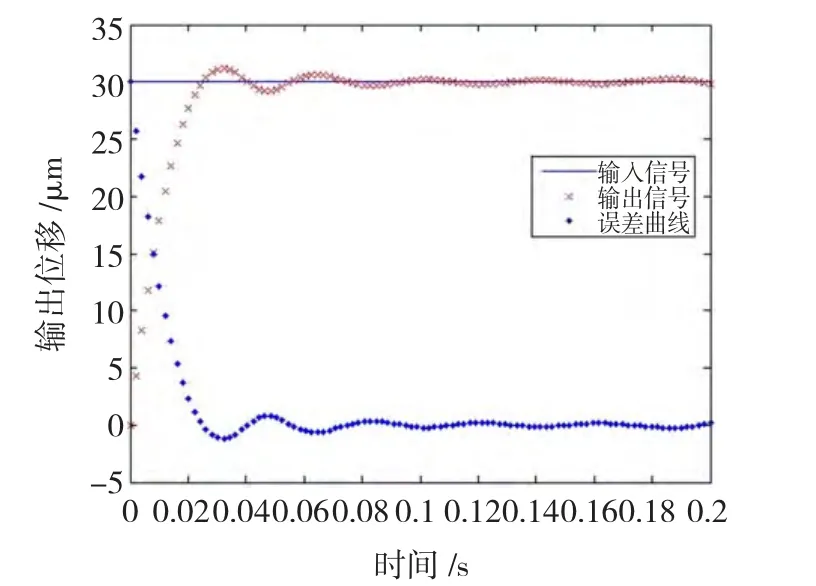
图7 PID控制阶跃响应Fig.7 Step response
三角波跟踪和正弦跟踪平均误差分别为0.41 μm和0.67 μm,见表3。

表3 控制效果比较Table 3 Positioning accuracy of different control schemes
4.2 基于PSO的PID自整定方案
实验按照定位实验和轨迹跟踪实验进行,阶跃响应选取30 μm阶跃信号,其实验响应曲线如图8所示,系统的调整时间0.06 s左右,超调在2%左右,稳定误差小于0.05 μm。

图8 PSO寻优PID阶跃响应Fig.8 Step response based on PSO
跟踪实验采用三角波和正弦波输入。三角波实验时,波纹管预加压伸缩到1 000 μm,误差曲线以1 000 μm为基准。正弦波输入频率为2.5 Hz,避免负值输入,输入从零值开始,数值偏向时间轴一侧。其轨迹跟踪效果如图9和图10所示。
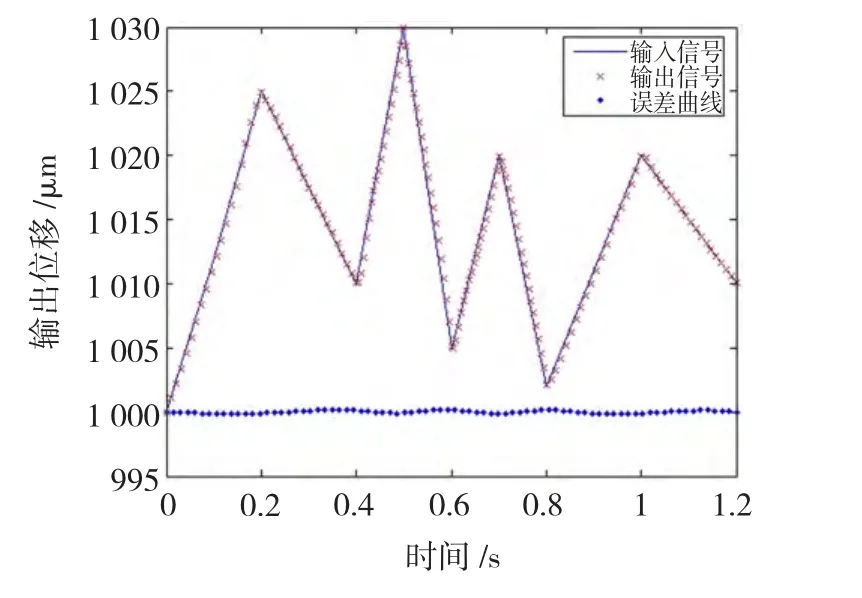
图9 锯齿波跟踪实验Fig.9 Sawtooth tracking experiment
从图中可以看出在PSO优化参数后的复合控制方案下,系统跟踪效果很好。三角波输入,跟踪最大误差为0.32 μm,平均为0.12 μm;正弦波输入,跟踪误差平均为0.18 μm,达到亚微米级或纳米级。满足超精密定位平台的需求。与传统PID控制相比,其平均误差和最大误差均有较大改进,见表3。

图10 正弦跟踪实验Fig.10 Sine tracking experiment
5 结论
本文设计了一种基于波纹管驱动的超精密运动平台,实验表明,实验平台定位精度达到了超精密定位的要求。波纹管驱动的定位平台在国内外研究和应用较少,其主要优点有:
1)波纹管驱动相比较电动驱动而言,波纹管采用气动作为驱动能量,环境干扰小,维护方便。
2)波纹管本身在较大行程中有着很高的定位精度,这一点是其他超精密驱动装置,如压电等所部具备的,因此在一些较大行程的超精密驱动中可以避免两级驱动的模式。采用PSO进行参数优化之后的复合控制方案,控制精度较高。
3)波纹管造价低廉,有着明显的价格和成本优势。
4)波纹管能量来源为气源,相对于电动而言,其驱动力的大小取决于管腔内的压力和波纹管截面积,因此在同等体积下,其输出推力相对于电机推力较大。
5)由于波纹管本身的柔性特性,可以考虑在一个平面内实现二维定位,从而避免的传统的“H”型结构,降低了系统的机械结构复杂程度,便于设计和控制,也降低了平台的硬件成本。
波纹管作为一种新型的驱动器件,研究表明其在超精密控制中有很好的应用前景,但是也存在诸多问题,目前还没有专门的企业生产驱动用波纹管,本实验中用到的波纹管为专门设计,其机械性能还有待进一步研究,其机械寿命也还需要进一步考虑和验证,希望更多地专家和学者给予关注。
[1]张从鹏,刘强.直线电机气浮精密定位平台设计与控制[J].北京航空航天大学学报,2008,34(2):224-228.
ZHANG Congpeng,LIU Qiang.Design and control of air bearing precision positioning stage driven by linear motors[J].Journal of Beijing University of Aeronautics and Astronautics,2008,34(2):224-228.
[2]赵兴玉,张胜泉,张大卫.基于音圈电机精密定位平台的控制系统设计与仿真[J],天津大学学报,2007,40(2):127-131.
ZHAO Xingyu,ZHANG Shengquan,ZHANG Dawei.Design and simulation of the control system of precision positioning table driven by voice coil actuator[J].Journal of Tianjin University,2007,40(2):127-131.
[3]SHINNO H,YOSHIKA H,TANIGUCHI K.A newly developed linear motor-driven aerostatic x-y planar motion table system for nano-machining[J].Annals of the CIRP,2007,56(1):369-372.
[4]冯晓梅,张大卫,赵兴玉,等.基于音圈电机的新型高速精密定位系统设计方法[J].中国机械工程,2005,16(16):1414-1418.
FENG Xiaomei,ZHANG Dawei,ZHAO Xingyu,et al.The new high-speed precision positioning system design methodology based on voice coil motor[J].Chinese Mechanical Engineering,2005,16(16):1414-1418.
[5]CHIANG M,CHEN C,TSOU T.Large stroke and high precision pneumatic-piezoelectric hybrid positioning control using adaptive discrete variable structure control[J].Mechtronics,2005(15):523-545.
[6]张建明.现代超精密加工技术和装备的研究与发展[J].航空精密制造技术,2008,44(1):1-7.
ZHANG Jiangming.Research and development of modern ultraprecision processing technology and equipment[J].Aviation Precision Manufacturing Technology,2008,44(1):1-7.
[7]王占彬,周浩洋,石朝锋,等.一种U型波纹管强度及稳定性分析方法研究[J].强度与环境,2012,39(4):19-24.
WANG Zhanbin,ZHOU Haoyang,SHI Chaofeng,et al.Research on the analytical method of U-shape bellows strength and Stabilization[J].Structure and Environment Engineering,2012,39(4):19-24.
[8]樊大均.波纹管设计学[M].北京:北京理工大学出版社,1988:60-93.
[9]刘强,张从鹏.直线电机驱动的H型气浮导轨运动平台[J].光学精密工程,2007,15(10):1540-1545.
LIU Qiang,ZHANG Congpeng.H-type air-bearing motion stage driven by liner motors[J].Optics and Precision Engineering,2007,15(10):1540-1545.
[10]陶家生.闭式双排节流孔矩形气浮导轨的计算方法[J].光学精密工程,1996,4(2):31-36.
TAO Jiasheng.Calculation of close double row orifice rectangular aerostatic slideways[J].Optics and Precision Engineering,1996,4(2):31-36.
[11]张新宇,陈忠基,姚瑶,等.基于有限元法的气浮支撑系统的数值模拟与实验研究[J].辽宁科技大学学报,2008,31(3/4):285-287.
ZHANG Xinyu,CHEN Zhongji,YAO Yao,et al.Numerical simulation based on finite element method and experiment of aerostatic bearing system[J].Journal of University of Science and Technology Liaoning,2008,31(3/4):285-287.
[12]王文,李欣欣.超精密定位平台的测量系统研究[J].机电工程,2006,23(4):13-16.
WANG Wen,LI Xinxin.Study on measurement system of ultraprecision positioner[J].Journal of Mechanical and Electrical Engineering,2006,23(4):13-16.
[13]KAWASHIMA K,ARAIA T,TADANO K,et al.Development of coarse/fine dual stage using pneumatically driven bellows actuator and cylinder with air bearings[J].Precision Engineering,2010,34(3):526-533.
[14]张栋,张承进,魏强.压电微动工作台的动态迟滞模型[J].光学精密工程,2009,17(3):549-556.
ZHANG Dong,ZHANG Chenjin,WEI Qiang.Dynamic hysteresis model of piezo-positioning stage[J].Optics and Precision Engineering,2009,17(3):549-556.
[15]赖志林,刘向东,陈振,等.压电陶瓷执行器多模时变滑模逆补偿控制[J].电机与控制学报,2012,16(1):92-103.
LAI Zhilin,LIU Xiangdong,CHEN Zhen,et al.Multi-mode time-varying sliding mode control of Piezoceramic actuator based on inverse compensation[J].Electric Machines and Control,2012,16(1):92-103.
[16]曹金凤,党选举,张凯.基于PI和神经网络混合模型的音圈电机迟滞建模[J].系统仿真学报,201l,123(2):386-389.
CAO Jinfeng,DANG Xuanju,ZHANG Kai.Hybrid hysteresis modeling of voice coil motor based on PI and neural network[J].Journal of System Simulation,201l,123(2):386-389.
[17]ANG Weitech,KHOSLA P K,RIVIERE C N.Feed forward controller with inverse rate-dependent model for piezoelectric actuators in trajectory-tracking applications[J].IEEE/ASME Transactions on Mechatronics,2007,12(2):134-142.
[18]党选举,姜辉,杨青,等.高频响音圈电机的复杂迟滞建模与验证[J].微电机,2012,45(6):1-5.
DANG Xuanju,JIANG Hui,YANG Qing,et al.Modeling and verify of complex hysteresis for high frequency voice coil motor[J].Micromotors,2012,45(6):1-5.
[19]王希花,郭书祥,叶秀芬,等.压电陶瓷迟滞特性的建模及复合控制[J].电机与控制学报,2009,13(5):766-771.
WANG Xihua,GUO Shuxiang,YE Xiufen,et al.Modeling and feed-forward control based on piezoelectric ceramic hysteretic[J].Electric Machines and Control,2009,13(5):766-771.
[20]崔玉国,董维杰,孙宝元,等.压电微动工作台的位移复合控制[J].机械工程学报,2006,42(3):156-161.
CUI Yuguo,DONG Weijie,SUN Baoyuan,et al.Displacement compounding control of piezoelectric micro-motion worktable[J].Optics and Precision Engineering,2006,42(3):156-161.
[21]KENNEDY J,EBERHART R.Particle swarm optimization[C]//Proceedings of IEEE international conference on neural networks,Nov 27-Dec 1,1995,Perth,Australia.1995,4(2):1942-1948.
[22]田艳兵.基于PSO的自整定PID温度控制研究[J].化工仪表自动化,2010,37(11):31-33.
TIAN Yanbing.The design of self-tuning PID temperature controller based on PSO[J].Control and Instruments in Chemical Industry,2010,37(11):31-33.

