基于改进Runge-Kutta型landweber的电容层析成像图像重建算法

陈宇， 陈德运

(1.东北林业大学信息与计算机工程学院，黑龙江哈尔滨 150040;2.哈尔滨理工大学计算机科学与技术学院，黑龙江哈尔滨 150080)

0 引言

随着20世纪80年代中期过程层析成像技术(process tomography，PT)的兴起和发展，该技术之一的电容层析成像技术(electrical capacitance tomography，ECT)成为众多科研工作者研究的对象［1－2］。ECT技术以两相流或者多相流为主要研究对象，可实现过程参数在线实时监测的功能，已广泛用于电力、能源、医药、石油等众多多相流检测领域［3］。因ECT技术可靠性高、成本低、结构简单、非入侵式、使用范围广、安全性强等优点，国内外研究者对ECT图像重建进行了大量研究并取得了较好的成果，成为当今图像重建领域研究发展的主流［4－5］。由于ECT技术是通过有限个数的电容值来重建图像，其“软场”效应和非线性的特点，使ECT系统的解极易随多项流体的变化而改变，稳定性差，很难用具体的数学解析式描述，致使图像重建难度增大［6－7］。因此深入研究探索更好的图像重建算法是当务之急。

国内外学者经过长期的研究，提出了很多ECT图像重建的算法，目前较常使用的方法有:线性反投影算法LBP［8］、landweber迭代算法［9］、基于模型的MOR算法、人工神经网络算法、共轭梯度算法［10］等。LBP算法是最早使用的简单成像法，运算速度快，但重建图像失真严重，效果较差。landweber迭代算法是在landweber迭代法的基础上求解欠定方程的图像重建算法，是目前应用最为广泛的算法，极大地提高了成像速度，但介质分界面仍存在明显的平滑效应。基于模型的MOR算法比LBP算法精确率高，但过程中需设定参数来描述介电常数分布情况，参数越多图像重建时间越长，因此消耗时间大是该方法的最大缺点［11］。神经网络法是通过建立电容值和图像像素灰度值之间的映射关系来实现图像重建，质量较高、响应速度快，但对于训练样本的完整性要求较高，且训练过程复杂、耗时大，在实际应用中难度较大。共轭梯度法(CG)收敛速度较快、稳定性高，但只适合系数矩阵为对称正定的情况，对复杂流型的图像重建效果不理想。各种方法都有自身的优点但也存在各自的局限性，还需不断研究加以完善。

本文在电容层析成像算法的基础上，提出一种改进R－K型landweber算法。该算法可以增强图像重建的稳定性，提高重建图像的质量。实验中采用多种算法对本文考察对象进行图像重建，结果表明本文提出的算法获得的重建图像的质量高于landweber、LBP、共轭梯度算法和最速下降法，为ECT技术图像

重建领域提供了一种有效可行的新方法。

1 电容层析成像系统基本原理

电容层析成像ECT系统由3部分组成:电容传感器、数据采集系统、成像计算机，如图1所示。其基本原理为由于不同物质的介电常数不同，介质分布浓度的变化会引起混合物的等价介电常数变化，致使测量的电容值随之改变。由此可依据实际测量的电容值来重建管道内介质的分布情况。

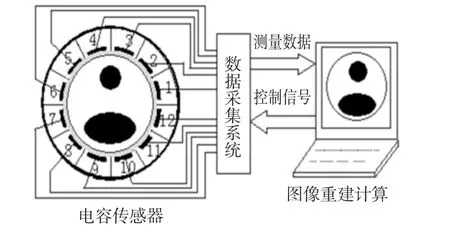
图112 电极电容层析成像系统的组成Fig.1 Composition chart of the 12-electrode ECT system

测量过程如下:以12个极板中的任意极板为起点，逆时针标记12个极板编号。选取电极板1为源极板(即公共电极)，剩余的2，3，…，12电极板为检测电极板。对源极板施加大小为U的固定电压，测量电极板对1－2，1－3，…，1－12之间的电容值，每次测量时闲置电极均需接地。上述操作后选取电极板2作为公共电极，其余为检测电极，依照之前的方法测量电极对2－3，2－4，…，2－12的电容值。依此类推，直到测量得到电极对11－12的电容值，完成整个测量过程。最终总共得到66个独立的电极对电容值。

目前，多数ECT成像算法是在介电常数到电容映射的线性模型基础上，经离散化、线性化和归一化建立的模型为

式中:C∈Rm×1是归一化电容向量;S∈Rm×n为系数矩阵(又称灵敏度矩阵);G∈Rn为归一化介质分布图像向量。ECT图像重建的关键在于根据给定的电容值C来求解介电常数的分布情况G。

2 算法原理

非线性算子方程为

其中:F是Hilbert空间上的一个非线性算子;H是Hilbert空间，具有相应的内积和范数［12］。

对于式(3)右边的观测数据不能得到准确值，只能得到具有一定误差扰动的yδ，且有

式中，δ表示误差水平。

当误差δ≠0时，通过求解初值问题，即

式中，0＜t＜T，xδ(0)=x0，可以获得解x*的正则化估计值xδ(T)，T代表正则化参数。用R级龙格－库塔(Runge－Kutta)方法求解式(5)，采用的离散化方程为

称式(6)为Runge－Kutta型landweber方法。当误差水平δ=0时，有

为了阐述方便，记

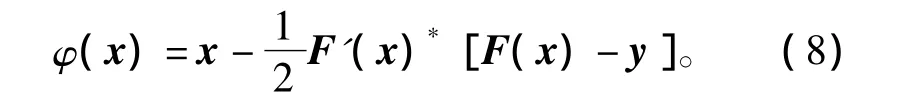
因为F(x*)=y，φ(x*)=x*，因此式(7)可以表示为

当误差水平δ≠0时，式(8)和式(9)可分别表述为

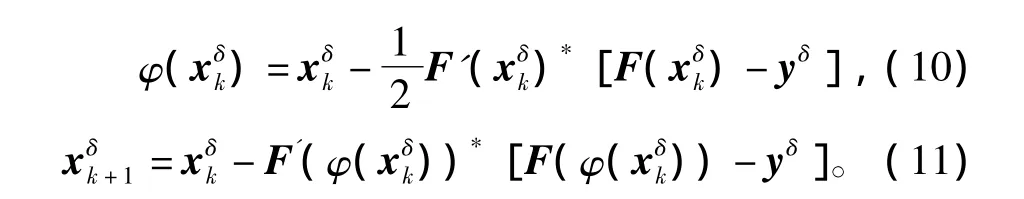
由上述理论可知，ECT重建算法中的电容向量C和图像分布向量G之间存在非线性关系为

将计算值和电容测量值的误差范数平方作为目标函数，则有

用灵敏度矩阵S取代F'(G)，以SGk取代F(G)，所以式(10)可以表示为

式(11)可以改写为

对于ECT系统，式(17)的迭代公式具有很高的收敛性，但需要的步长较多，属于小步长搜索。

考虑到ECT系统的传统landweber迭代公式为

式(18)的右边的梯度用hk表示为

由式(18)和式(19)，则知图像向量G的第k+1次迭代格式为

可知landweber算法的每次迭代的搜索方向就是负梯度方向，由于该步长较大，可以很快到达收敛区域。但到达收敛区域后，在向真正的解逼近时，会由于算法自身的缺陷，而只能得到一个解的近似。且当跳过收敛域后，迭代解和真解之间的距离会变大。故考虑每次迭代时先用landweber算法进行搜索，然后再用Runge－Kutta型landweber算法的迭代步进行精细搜索，以得到更准确的解，同时提高了收敛速度。算法的最终迭代步可以写成

下对本文所提出算法的收敛性进行分析:设

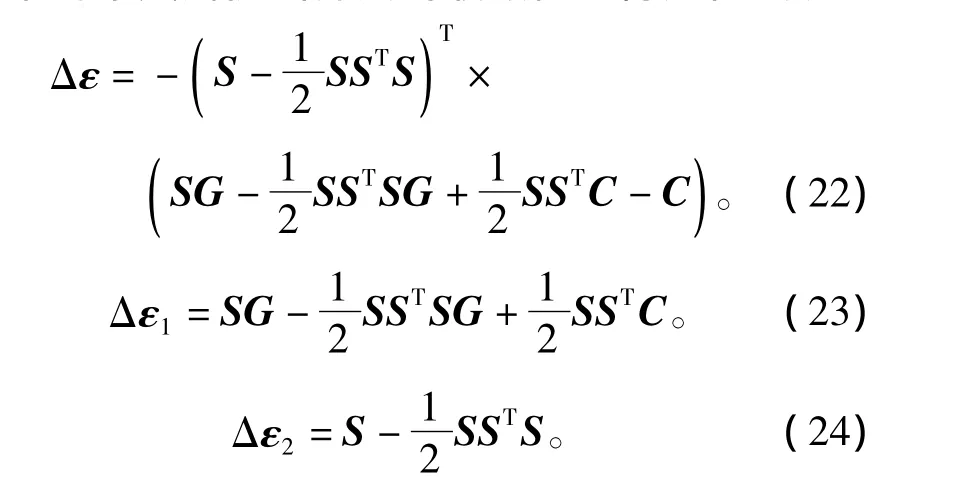
对于Runge－Kutta迭代公式(17)，有

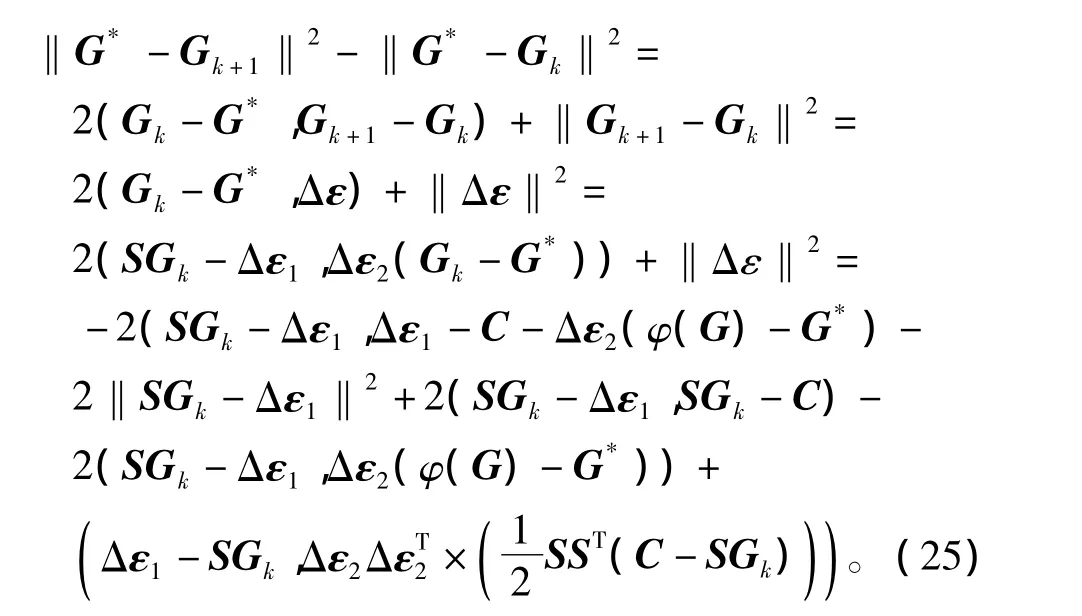
假设C=SG的解G*的邻域内，算子满足非线性条件

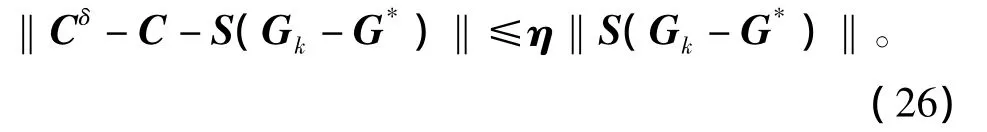
式中，0＜η＜0.5，并设δ代表误差水平，L代表范数上界，则有

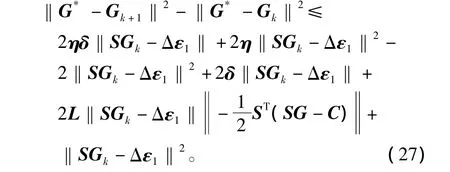
又因为

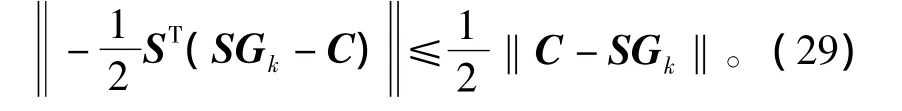
由式(26)有

由式(28)有

按广义偏差原则，有

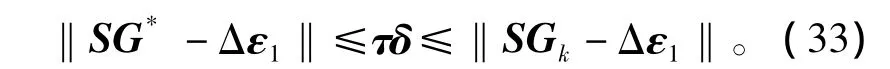
式中，τ是依赖于η的正数，且τ满足

进一步有

由式(33)和式(34)，可以得出式(32)不等式右边为负数，说明Gk+1比Gk更单调收敛接近于真解。

对于landweber的迭代公式(18)，有

由Morozov偏差原则

则可知式(35)的不等式右边为负数，说明式(18)中的Gk+1比Gk更单调收敛接近于真解。综上可知式(21)迭代公式是单调的，且逐渐逼近真解。

每次迭代过程都要对图像从物理意义的角度进行修正，即在每次迭代循环中引入Gk的估计值应在0和1.0之间的先验信息。为此，式(21)修改成投影迭代为

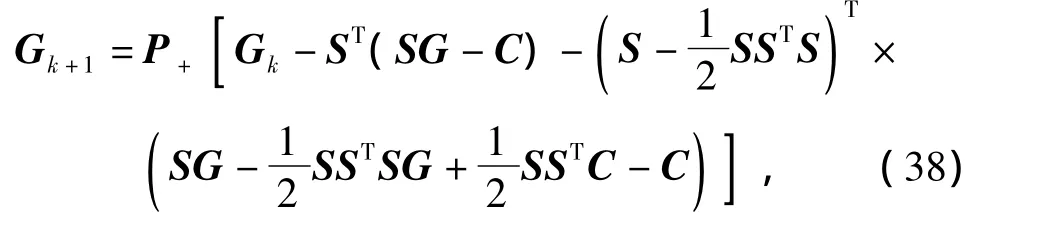
式中，P+是非负凸集上的投影，且有

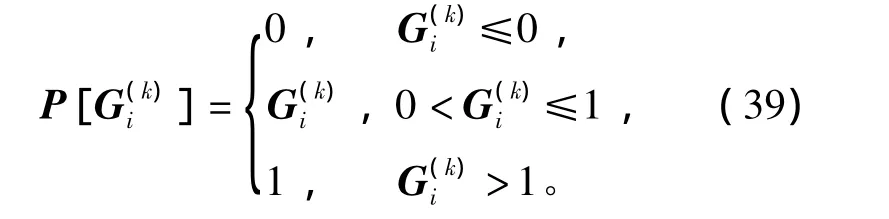
其中，G(k)代表列向量G第k次迭代的第i个分量。为保证每次迭代得到的解都为有限非负值，投影算子需确保每次迭代都收敛于一个凸集。实验表明，通过施加投影算子来引入了物理意义上的约束的方法，在一定程度上可以加快重建速度、提高重建图像的质量。

3 仿真与实验结果

本研究采用12电极系统应用Matlab软件进行仿真实验，验证该算法性能。实验中，用32×32的网格将管道截面分为1024个像素，其中856个成像单元为该界面的有效区域。实验时需先为极低位层流、柱状流、小半径核心流和低位层流进行预设置，再采用本文提出的(improved Runge－Kutta type landweber，简称IRKL)算法进行图像重建。同时采用线性反投影法(LBP)、共轭梯度法(CG)、最速下降法(SD)和landweber迭代法重建图像，并与IRKL算法的重建图像质量进行比较，所有成像图像采用阈值进行了滤波处理。

图像重建的速度用迭代次数N表示，N越大表示重建时间越长，重建速度越慢。由于LBP算法为单步处理，故N=0。迭代次数N的选取需由数值实验确定。典型方法为迭代误差满足

就停止迭代。大量实验表明，本文IRKL算法的迭代次数N通常选取十几(简单模型)到几十(复杂模型)之间就可得到较好的成像效果。

成像完成后需要分析重建图像的质量。实验选用空间图像误差作为评判图像质量的标准，定义为

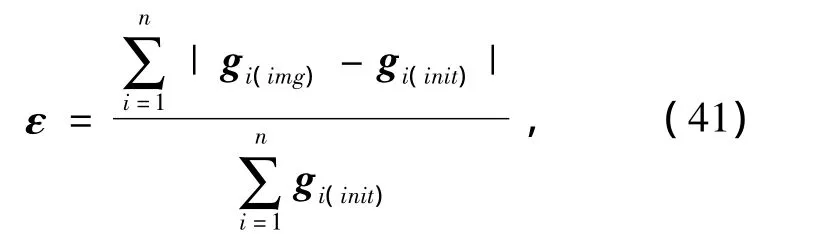
其中:gimg为重建图像向量;ginit为介质分布原型图像向量;i为成像区域剖分单元索引;n为成像区域单元总数。

成像结果的比较如图2所示(黑色区域是水，白色区域是变压器油)。

图2 成像结果的比较Fig.2 Comparison of reconstructed tomograms

从成像结果可知，LBP算法的重建图像大体接近原流型，而landweber、SD算法和本文的IRKL算法的重建图像则十分接近原流型。IRKL算法对于极底位层流的成像效果相对要好，最接近原始流型，且明显减缓了边界模糊效应。表1为重建图像误差比较，结合图2结果可知，对于低位层流和柱状流，LBP误差最大;对于极低位层流，CG法误差最大;对于小半径核心流，SD算法误差最大;而对于这四种流型，IRKL算法产生的误差最小，且电容值混入了5%的高斯白噪声后，该算法仍然能较好的进行图像重建，表现出了较强的抗噪声能力。表2表明，IRKL算法同landweber法和SD算法的迭代步数相近，而同CG迭代步数相差较大。从以上分析可以看出，使用改进Runge－Kutta型landweber的图像重建算法，其成像的精度和质量比LBP、landweber、CG和SD算法要好。

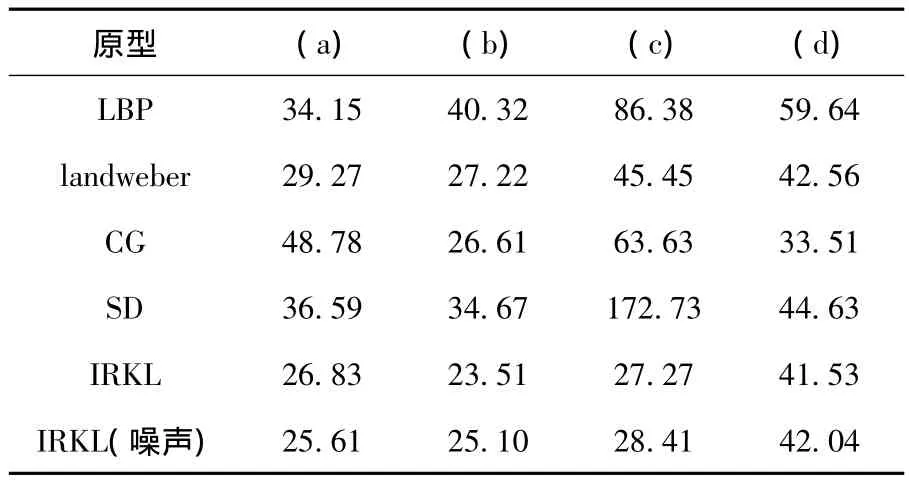
表1 图像误差Table 1 Image error/%

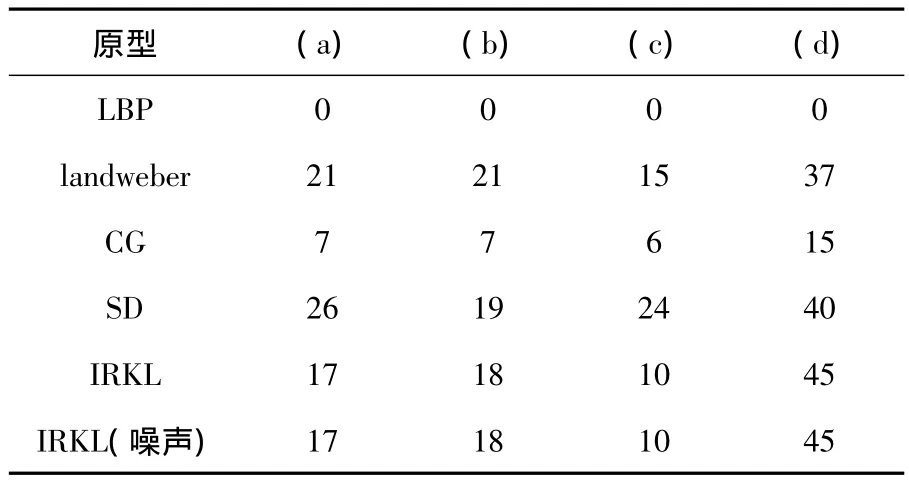
表2 迭代步数Table 2 Number of iteration

4 结语

本文提出了一种改进的Runge－Kutta型landweber的正则化迭代电容层析成像算法(IRKL)，在分析ECT反问题病态性的基础上，采用迭代求解时广搜和精搜同时进行的策略，并利用范数残量误差的性质分析了改进的Runge－Kutta型landweber算法的收敛性。该算法程序简单、所需存储量小、成像精度高、抗噪声能力强且易于满足收敛条件。数值实验结果表明该算法的重建图像更接近原流型，且质量远远优于传统的LBP、SD、landweber和CG算法，为ECT图像重建技术提供了一种有效可行的新方法。

未来将把研究重心放在复杂流型的自动辩识领域，在迭代的过程中加入补偿算法以此减少测量误差，进一步提高图像重建质量，使ECT图像重建技术更广泛地应用于生产实践。

［1］郭志恒，律德才，邵富群.基于差分灵敏度模型的电容层析成像图像重建方法［J］.中国电机工程学报，2012，32(23):75－82.

GUO Zhiheng，LU Decai，SHAO Fuquan.Image reconstruction method for electrical capacitance tomography based on the different sensitivity model［J］.Proceedings of the CSEE，2012，32(23):75－82.

［2］RIMPILAINEN V，HEIKKINEN L M，VAUHKONEN M.Moisture distribution and hydrodynamics of wet granules during fluidized－bed drying characterized with volumetric electrical capacitance tomography［J］.Chemical Engineering Science，2012，75(18):220－234.

［3］李岩，朱艳丹，袁小花，等.基于ANSYS电容层析成像结构参数分析与优化［J］.哈尔滨理工大学学报，2012，17(1):54－58.

LI Yan，ZHU Yandan，Yuan Xiaohua，et al.Analysis and optimization of structural parameters based on ANSYS in ECT［J］.Journal of Harbin University of Science and Technology，2012，17(1):54－58.

［4］周云龙，衣得武，高云鹏.基于混合模型电容层析成像系统敏感矩阵建立［J］.哈尔滨理工大学学报，2012，17(2):40－44.

ZHOU Yunlong，YI Dewu，GAO Yunpeng.Sensitivity matrix construction in electrical capacitance tomography system based on mixed models［J］.Journal of Harbin University of Science and Technology，2012，17(2):40－44.

［5］OSTROWSKI K L，LUKE S P，WILLIAMS R A.Simulation of the performance of electrical capacitance tomography for muasurement of dense phase pneumatic conveying［J］.Chemical Engineering Journal，1997，68(2/3):197－205.

［6］HJERTAKER B T.Static characterization of a dual sensor flow imaging system［J］.Flow Measurement and Instrumentation，1998，9(3):183－191.

［7］LIU S，YANG W Q，WANG H，et al.Investigation of square fluidized beds using capacitance tomography:preliminary results［J］.Measurement Science and Technology，2001，12(8):1120－1125.

［8］XI Shaolin，ZHAO Fengzhi.Computation Methods for Optimization［M］.Shanghai:Shanghai Scientifie＆Technical Publishers.1983:113－117.

［9］YANG W Q，PENG L H.Image reconstruction algorithms for electrical capacitance tomography［J］.Measurement Science and Technology，2003，14(1):R1－R3.

［10］周云龙，衣得武，高云鹏.基于INGA的电容层析成像图像重建算法的研究［J］.制造业自动化，2012，34(11):81－86.

ZHOU Yunlong，YI Dewu，GAO Yunpeng.Imaging reconstruction algorithm based on improved niche genetic algorithms for electrical capacitance tomography system［J］.Manufacturing Automation，2012，34(11):81－86.

［11］LIU S，FU L，YANG W Q，et al.Prior-online iteration for image reconstruction with electrical capacitance tomography［J］.IEE Proceedings Science，Measurement and Technology，2004，151(3):195－200.

［12］HANKE M，NEUBAUER A，SCHERZER O.A convergence analysis of the landweber iteration for nonlinear ill-posed problems［J］.Numerische Mathematik，1995，72(1):21－37.