非晶合金J-A模型修正
李超, 徐启峰
(福州大学电气工程与自动化学院,福建福州 350108)
0 引言
非晶合金具有矫顽力低、导磁率高、损耗小等优点,近年来在变压器、互感器、电磁开关等电力设备中得到了广泛应用[1-2]。电力设备运行时环境温度变化范围大,因此必须了解磁心材料的温度特性;同时为了防止磁心饱和,常采用气隙磁心结构,而目前对非晶合金温度特性和带气隙磁心磁滞模型的研究较少,因此建立一个能够反应温度、气隙变化的非晶合金磁滞模型具有实用价值。
J-A模型符合磁滞现象的物理本质且模型参数少,在铁磁材料的磁滞建模领域得到了广泛应用[3-4],因此本文选取J-A模型对非晶合金磁滞建模。但J-A模型不能反应材料的温度特性,也未考虑磁致伸缩、热膨胀等因素。本文增加了磁致伸缩系数、热膨胀系数,并修正了J-A模型的其他参数,提出了一种计及温度、气隙参数的非晶合金磁滞建模方法,并实验验证了方法的有效性。
1 J-A模型介绍
J-A理论认为非磁性夹杂、晶界、内应力等牵制点的存在使畴壁取代的磁化过程受阻而导致磁滞[2-3],并将磁化强度M分解为不可逆磁化分量Mirr和可逆磁化分量Mrev两部分[3-5],即

不可逆分量、可逆分量可分别表示为
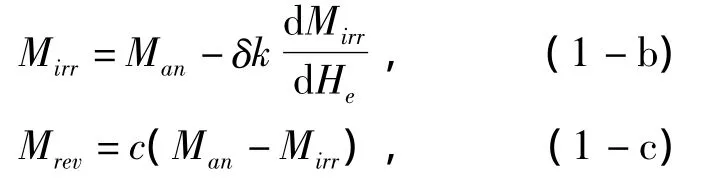
其中:Man为非磁滞磁化曲线,其公式为
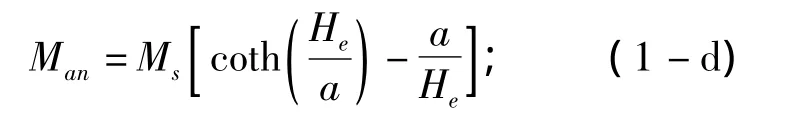
He为有效磁场强度,公式为

联立公式可推导出M-H的关系式为
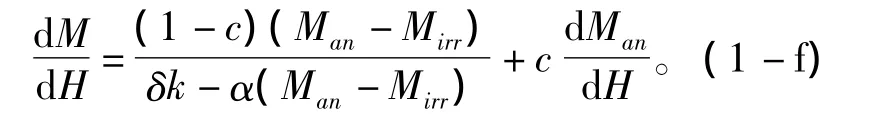
根据B=μ0(H+M)可进一步得到B-H曲线。
J-A模型包含5个参数,其中Ms表示饱和磁化强度;c为可逆磁化系数;α为表征磁畴内部耦合的平均场参数;k表示损耗系数;a为表征无磁滞磁化曲线的形状参数[3]。其中Ms可通过材料手册或实验得到,c、α、k、a可通过公式组(2)得到,即
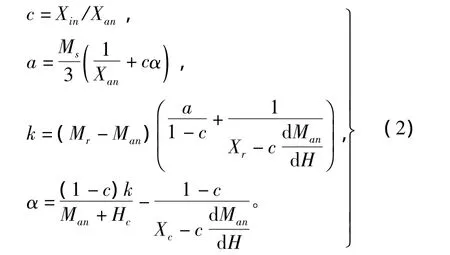
其中:Mr为剩余磁化强度;Xin为初始磁化曲线相对初始导磁率;Xan为无磁滞磁化曲线相对初始导磁率;Xc为磁滞回线矫顽力点的相对微分磁化率;Xr为磁滞回线剩磁点的相对微分磁化率[3]。
文献[6]详细分析了5个参数对磁滞回线的影响,结果如表1所示。
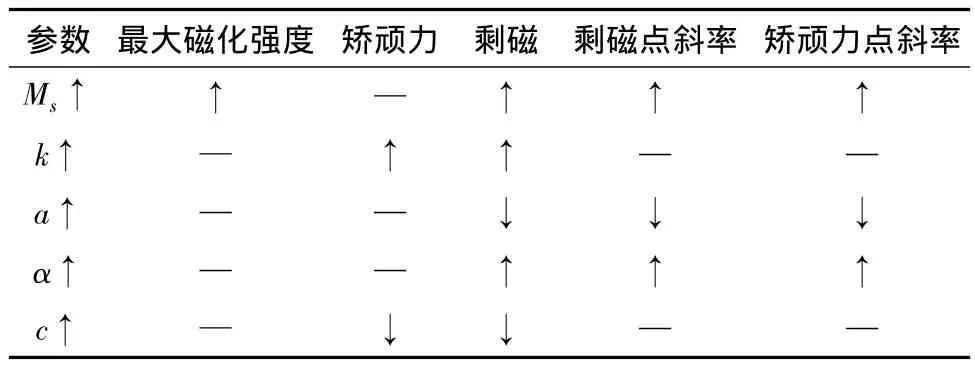
表1 参数对磁滞回线的影响Table 1 The effect of parameters on hysteresis loops
从表1可见,最大磁化强度只由Ms确定;矫顽力受c、k共同影响,矫顽力点和剩磁点的斜率受Ms、α、α影响。经典J-A模型无法反应磁滞回线随温度变化情况,但可以通过测量不同温度下剩余磁化强度、矫顽力、矫顽力点斜率、剩磁点斜率,最大磁化强度的变化,并建立不同温度下J-A模型,推导出J-A模型参数随温度的变化曲线并可拟合出J-A模型参数随温度变化公式,进而将温度参数引入J-A模型。
2 非晶合金J-A模型建模
2.1 非晶合金的温度特性
为了便于说明非晶合金材料温度特性的复杂性,列出非晶合金、硅钢片和电工纯铁的最大导磁率和矫顽力随温度变化曲线如图1所示。

图1 最大导磁率、矫顽力随温度变化曲线Fig.1 Variation of maximum effective permeability and coecivity with temperature
3种材料的矫顽力均随着温度上升而减小,但最大导磁率随温度变化趋势不同。硅钢片和电工纯铁的导磁率随温度上升而减小,到达居里温度Tc附近时,导磁率急剧下降,接近于零[7];而随着温度的上升,非晶合金导磁率先增大后减小。温度对非晶合金的影响体现在原子热运动、磁畴转动和畴壁移动方面[8]。
1)低温时,电子运动与磁畴运动受到的约束力较大,磁畴磁矩有序排列,导磁率低;随着温度的上升,电子运动、磁畴转动和畴壁移动受到的约束力变小,导磁率增加,矫顽力降低,磁心损耗降低。当升高至某温度时,导磁率、饱和磁化强度达到最大值,定义此温度为Tb。
2)高于Tb,低Tc时:随着温度的上升,金属原子热运动加剧,使磁畴磁矩排列发生混乱,导磁率减小。
3)高于Tc时:由于高温下原子的剧烈运动,磁畴磁矩的排列混乱无序,非晶合金失去了磁性。
2.2 闭合磁心J-A模型温度特性修正
根据不同温度下的磁滞回线建立J-A模型,得到模型参数随温度变化曲线如图2所示。

图2 J-A模型参数随温度变化曲线Fig.2 Variation of J-A model parameters with temperature
文献[9-10]根据平均场理论对镍和电工纯铁的J-A模型进行了温度修正,由于非晶合金与电工纯铁等温度特性的差异,文献[9-10]提出的参数修正公式只适用于Tb与Tc之间的范围,Tb以下温度时需提出新的修正公式。而电力设备运行的环境温度通常处于Tb以下,此温度范围内的修正公式更具有实用价值。本文根据非晶合金温度特性,提出了分段修正方法:
1)当温度高于Tc时,非晶合金发生晶化,磁性消失,饱和磁化强度公式为

2)当温度高于Tb、低于Tc时,根据文献[9-10]的平均场理论,得到修正公式为

式中,β为临界指数,可通过测量Tb与其他温度下的M-H曲线来确定。根据Tb下M-H曲线得到Ms(Tb),其他温度下的M-H曲线得到Ms(T),代入式(4)得到初始的临界指数β。这个指数存在一定的误差,需要进一步修正,可对多条M-H曲线通过迭代求解的方法确定β值[6]。
居里温度Tc的测量方法有很多,其中有Ms-T曲线法、感应法、磁电阻效应法等[11]。目前通过物理性能测试仪PPMS测量Ms-T曲线的方法最为精确,即Ms接近零时的温度即为此材料的居里温度。Tb为Ms-T曲线中饱和磁化强度最大值对应的温度。
3)温度低于Tb时,由多组数据提出拟合公式为

式中,γ、δ、ε、η、φ 为修正系数。与临界指数 β的确定方法一样,修正系数可通过建立两个不同温度下的J-A模型、将参数代入式(5)得到初始修正系数,最后对多条M-H曲线通过迭代求解得到最佳修正系数。
将修正公式(4)或式(5)代入J-A模型得到不同温度下的磁滞回线。本文对一种铁镍基非晶合金磁环进行了实验验证,图3(a)是温度为258 K、358 K(低于Tb)时的实验与仿真波形图。图3(b)是温度为483 K、523 K(高于Tb)时的实验与仿真图。从图3可见,仿真与实验结果一致:低于Tb时,随着温度的上升,最大磁化强度增大、矫顽力减小;高于Tb,低于Tc时,随着温度的上升,最大磁化强度降低,矫顽力减小。
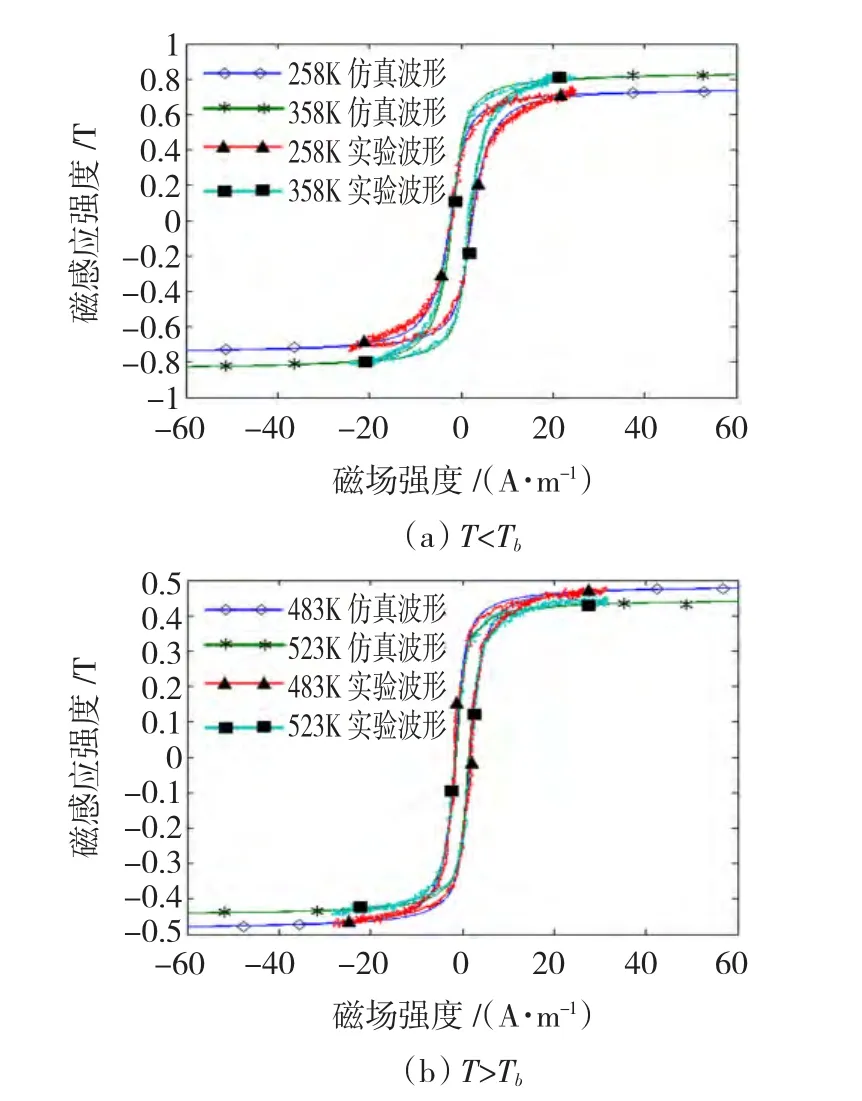
图3 磁滞回线仿真与实验波形Fig.3 Simulated and measured hysteresis loops
3 非晶合金磁滞模型的气隙修正
为防止磁饱和,通常对磁环采取开气隙的措施,文献[12]基于J-A模型提出了气隙磁心的建模方法。假设气隙平滑且与磁力线方向垂直,不考虑漏磁等问题,可认为气隙长度Lair(单位m)就是气隙中平均磁力线的长度,磁心气隙处的磁感应强度Bair等于磁心横截面上的磁感应强度Bcore(单位T)。

由安培环路定理,将励磁电流I(单位A)折算到一匝得
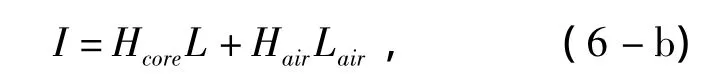
其中Bcore可根据闭合磁心的J-A模型仿真得到

Hcore(单位A/m)由J-A模型仿真的B-H曲线表示为最
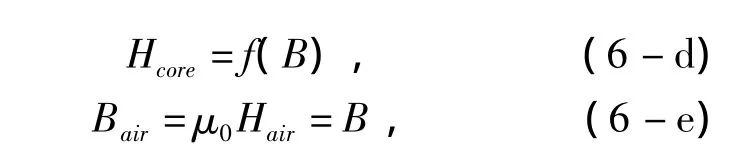
终得到气隙磁心的磁滞回线公式为

J-A模型仿真的B-H函数关系H=f(B)与式(7)联立,可得到气隙磁心的磁滞回线。
本文对一个气隙为0.1 mm的非晶合金磁心进行仿真和实验验证,结果如图4所示,原模型存在以下问题:
1)仿真波形斜率较低,与实验结果差异较大。
2)温度特性仿真结果与实验结果不一致。磁滞回线非饱和段实验波形如图所示,磁感应强度在85℃时低于-15℃时的数值,而仿真结果与之相反。

图4 非晶合金带气隙磁芯磁滞回线仿真与实验波形Fig.4 Simulated and measured hysteresis loops for amorphous core with air gap
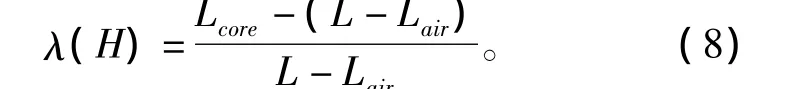
这是由于非晶合金的磁致伸缩系数比一般硅钢片大3~5倍,某些配方导致气隙长度变化明显。原模型未考虑磁致伸缩的影响,使得仿真波形斜率低于实验波形,温度特性的仿真结果与实验结果也有差异。因此需要对文献[12]中的模型进行优化。设磁场强度H下磁致伸缩系数为λ(H),未加磁场时磁心的平均磁路长度为L-Lair。加入磁场后设磁心的磁路长度为Lcore,表达式为
则加入磁场后气隙新长度Lair(H)为
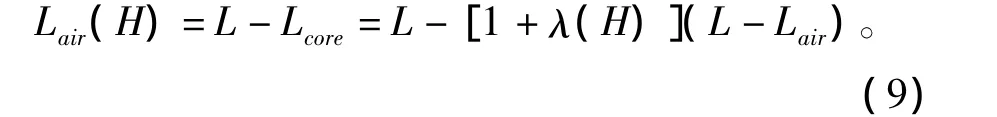
式(7)修正为

根据式(10)进行仿真,波形如图5所示,优化后模型的仿真结果与实验结果一致。
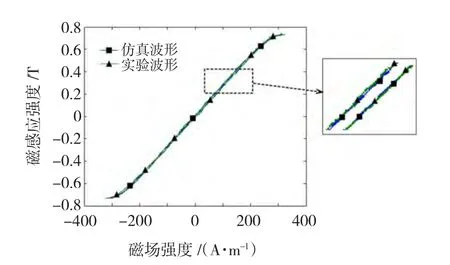
图5 优化后磁滞回线仿真与实验波形Fig.5 Optimized and measured hysteresis loops for amorphous core with air gap
4 温度与气隙综合修正及应用
4.1 温度与气隙综合修正方法
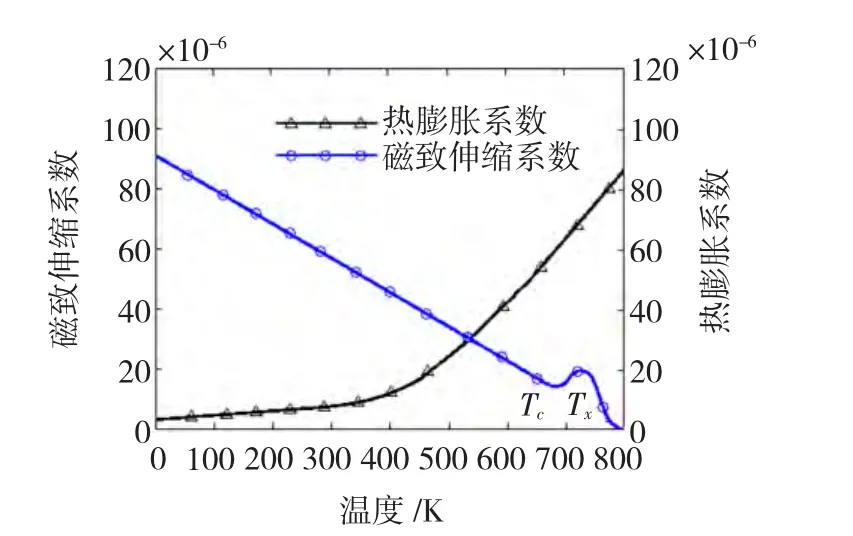
图6 磁致伸缩系数和热膨胀系数随温度变化曲线Fig.6 Variation of magnetostriction coefficient and thermal expand coefficient with temperature
如图4所示,原模型对温度特性仿真结果与实际不符,这是由于磁致伸缩系数随温度变化和热膨胀所致。因此对气隙磁心引入温度修正,需要考虑温度对磁致伸缩系数的影响和热膨胀问题。文献[13]介绍了非晶合金磁致伸缩系数的温度特性,文献[14]介绍了非晶合金热膨胀系数的温度特性。如图6所示,低于Tc时,磁致伸缩系数随温度上升而减小;大于Tc后,温度继续上升使非晶合金发生晶化,导致磁致伸缩系数先增大后减小,到达晶化温度Tx后,磁致伸缩系数减小至零[13]。而热膨胀系数随温度上升呈指数增大。
式(10)进一步修正,设磁致伸缩系数为λ(H,T),热膨胀系数设为ξ(T)。同时考虑热膨胀与磁致伸缩时,磁心的磁路长度Lcore(H,T)为
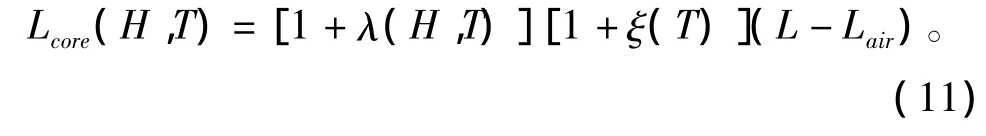
气隙新长度为

式(10)进一步修正为
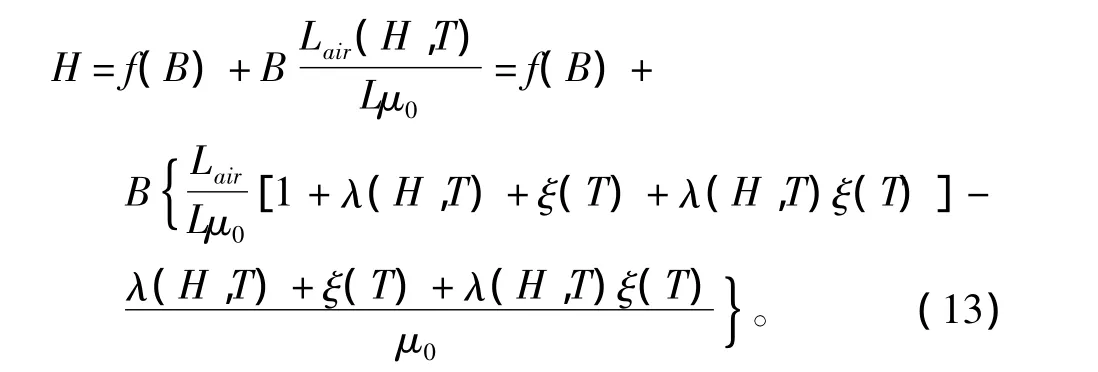
根据式(13)可得到带温度参数和气隙参数的磁滞模型。仿真时计算流程图如图7所示。对于闭合磁心的磁滞回线可根据式(1)、式(4)、式(5)进行仿真;对于固定温度下气隙磁心的磁滞回线,可根据式(1)、式(10)进行仿真;温度与气隙综合修正时,可根据式(1)、式(4)、式(5)、式(13)进行仿真。

图7 仿真流程图Fig.7 The simulation flow chart
4.2 模型的简化
电力设备运行的环境温度在-40~85℃,一般低于温度点Tb,在此温度范围内简化新模型。
1)温度修正公式需测量Tb温度下的J-A模型参数。由于Tb较高,一般的实验室不具备测试条件。为了便于模型在电力系统中应用,将式(5)进行变换。设室温T0为基准温度,代入式(5)得

式(5)与式(14)联立得

同理可得其他参数的公式为
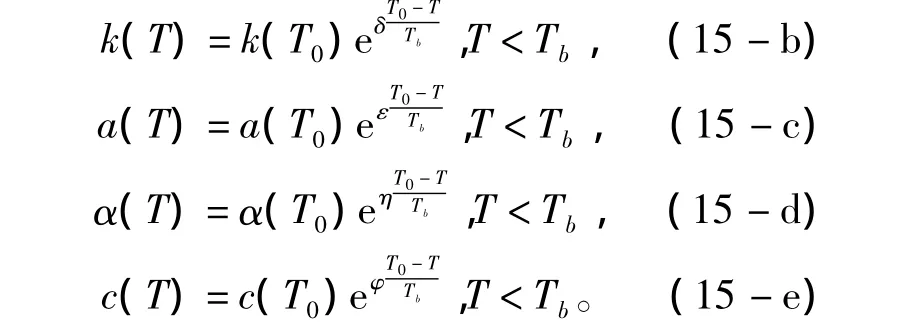
测量基准温度下J-A模型参数,并确定Tb和修正系数,可建立低于Tb温度时的磁滞模型,降低了建模的难度。
2)如图6所示,在低于Tb的范围内,随着温度的上升,非晶合金磁致伸缩系数减小。同时对于气隙磁心,当外部磁场强度较大,可认为非晶合金的磁致伸缩系数已经达到饱和,不随磁场强度发生变化。因此磁致伸缩系数为λ(H,T)的表达式拟合为
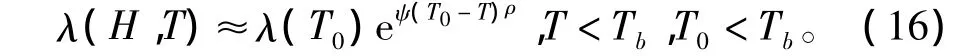
其中:λ(T0)为T0温度时数据;ψ、ρ为修正系数。
由图6可见,在低于Tb的范围内,随着温度的上升,热膨胀系数ξ(T)呈指数上升,ξ(T)表达式可拟合为

其中:ξ(T0)为T0温度时的数据;θ、ω为修正系数。考虑到磁致伸缩系数和热膨胀系数的数量级均为10-6,因此 λ(H,T)ξ(T)可忽略不计。式(13)简化为
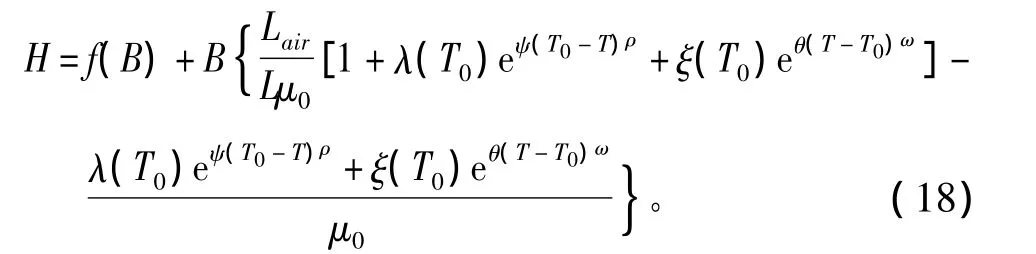
只需要测量常温下的J-A模型参数、磁致伸缩系数、热膨胀系数等,即可根据式(1)、式(15)、式(18)进行仿真,简化了新模型。
5 新模型应用及实验验证
以集磁式光学电流互感器为例,其要求气隙中磁场强度具有稳定的温度特性,否则将引起测量误差。在此,利用新模型的仿真结果提出了一种利用铁镍基非晶合金磁致伸缩特性和温度特性相互作用,从而具有稳定温度特性的磁心设计。
如图6所示,温度低于Tb时,随着温度的上升,热膨胀系数增大、磁致伸缩系数减小,但热膨胀系数变化量远小于磁致伸缩系数的变化量,因此最终导致气隙长度增大,导磁率减小;而非晶合金的导磁率随温度升高而增大。两者对磁滞回线的作用相反。因此通过选取合适的参数,在某一温度范围内,极限磁滞回线的非饱和段和次级磁滞回线将具有稳定的温度特性。由于电力设备的磁心大部分工作在非饱和状态,本设计具有实用价值。
设计的关键在于选取合适的气隙长度和非晶合金材料。设空气气隙部分B-H曲线的斜率为kp,有

kp随着温度T变化曲线如图8(a)所示,随着温度的上升,kp减小,证明了气隙会使导磁率随温度的上升而降低。kp随着气隙长度Lair变化曲线如图8(b)所示,随着气隙长度的增大,kp成指数减小,气隙较小时,磁致伸缩和热膨胀使气隙长度变化百分比较大,对气隙磁心温度特性的影响也较大;随着气隙长度的增大,磁致伸缩和热膨胀对气隙长度的影响程度变低,其温度特性与闭合磁心的温度特性逐渐接近。因此可通过选择气隙长度进行调节。
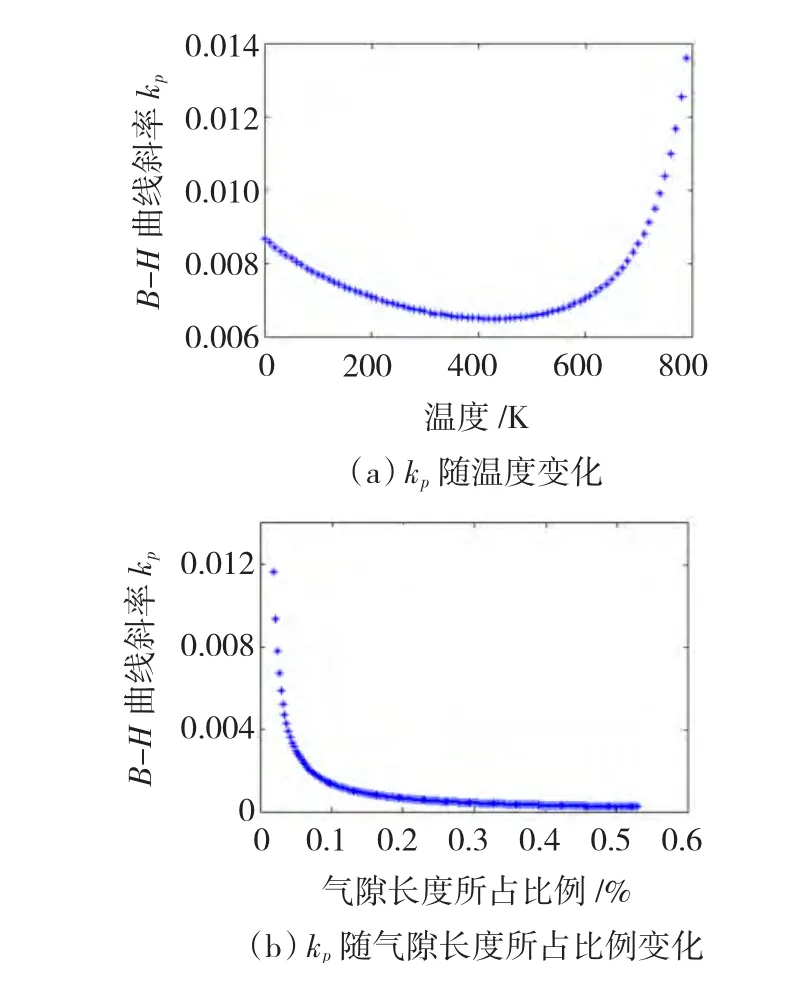
图8 kp随温度或气隙变化曲线Fig.8 Variation of kpwith temperature or air gap
而非晶合金导磁率随温度变化的程度,与合金配方、退火温度、退火时间等有关[15]。可根据设计要求,选取合适的非晶合金。当气隙长度与非晶合金材料匹配时,可得到具有稳定温度特性的气隙磁心。对一种铁镍基非晶合金进行建模得到仿真波形如图9所示。随着温度的上升,气隙较小时,磁滞回线下移;气隙较大时,磁滞回线上移;选取合适气隙后,非饱和段磁滞回线导磁率基本不变,具有稳定温度特性。针对本文采用的铁镍基非晶合金,由图9知,气隙长度为0.2 mm时,气隙中磁场强度具有稳定温度特性,适合于集磁式光学电流传感器。

图9 带气隙磁心磁滞回线仿真波形Fig.9 Simulated hysteresis loop for air gapped core

图10 铁镍基非晶合金磁心结构图Fig.10 Structure of Fe-Ni-based amorphous cores
所采用的铁镍基非晶合金镍含量超过50%,具有较大的磁致伸缩系数和居里温度,其居里温度为370℃、晶化温度为520℃,Tb为124℃。根据25℃、50 Hz条件下的实验数据建立J-A模型,具体参数为Ms:6.268×105;k:8.458 9;a:4.757 2;α:8.572×10-6;c:0.021 5。温度修正系数及气隙长度修正系数为 γ:-0.554,ε:0.566,δ:0.845,η:0.678,λ(25℃):70×10-6,ξ(25℃):7.5×10-6,φ:-0.857,β:0.686,ψ:0.002,ρ:0.98,θ:0.006,ω:1。
非晶合金闭合磁心的仿真与实验波形已在图4中,证明了模型的有效性,表明在电力设备运行的环境温度范围内,非晶合金导磁率随着温度的上升而增大,这与硅钢片、电工纯铁等传统铁磁材料的温度特性相反。
实验室设计的光学电流互感器工作温度范围为-15~85℃。选取-15℃,85℃为实验温度,分别对0.1 mm、0.2 mm和1 mm气隙磁环测量磁滞回线。实验与仿真波形如图11所示。可见随着温度的上升,0.1 mm气隙磁环磁滞回线下移,其温度变化趋势与闭合磁心相反;0.2 mm气隙磁环的矫顽力随着温度的上升而减少,导致温度高时回线面积较小,但两条曲线的斜率保持一致,本磁环基本具有稳定的温度特性;1 mm气隙磁环的磁滞回线随温度上升而上移。
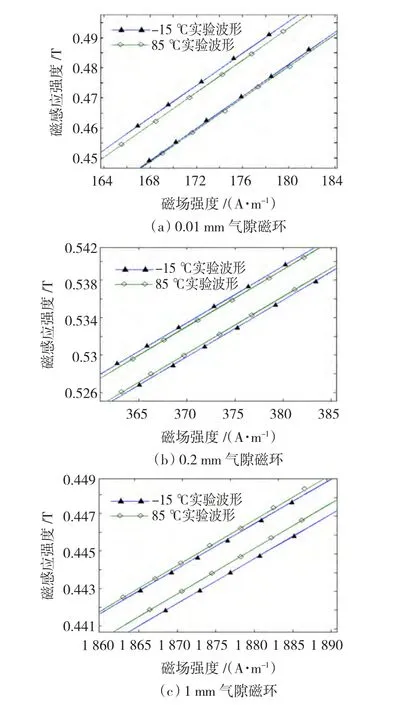
图11 铁镍基非晶合金带气隙磁心磁滞回线实验波形Fig.11 Measured hysteresis loops for an Fe-Ni-based amorphous core with air gap
6 结论
1)提出了非晶合金J-A模型的温度修正方法,弥补了J-A模型无法反应温度特性的缺点。
2)优化了气隙磁心的磁滞模型。通过修正磁致伸缩对气隙长度的影响,提高了对气隙磁心的仿真准确度。本方法也适用于其它铁磁材料。
3)对非晶合金磁心建立了带温度参数和气隙参数的磁滞模型。通过对一种铁镍基非晶合金磁心的实验验证,证明了模型的有效性。
4)提出了一种具有稳定温度特性的气隙磁心设计方法。选取合适的气隙长度和非晶材料,可使磁滞回线非饱和段的导磁率在一定的温度范围内基本保持不变。本方法为一些需要稳定温度特性磁心的设备提供了设计思路。
5)本文提供的实验数据和建模方法具有实用价值,可用于互感器、变压器等磁场与温度场的耦合仿真研究、气隙设计、磁性材料的选择等。
[1]ZHANG Yu,LIU Jinliang,FENG Jiahuai.Saturation and short pulse response characteristics of the Fe-based amorphous core with a small air gap[J].IEEE Transactions on Plasma Science,2012,40(1):90-97.
[2]PROCHAZKA R,HLAVACEK J,DRAXLER K.Impulse current transformer with a nanocrystalline core[J].IEEE Transactions on Magnetics,2013,49(1):77-80.
[3]李贞,李庆民,李长云,等.J-A磁化建模理论的质疑与修正方法研究[J].中国电机工程学报,2011,31(3):124-131.
LI Zhen,LI Qingmin,LI Changyun,et al.Queries on the J-A modelling theory of the magnetization process in ferromagnets and proposed correction method[J].Proceedings of the CSEE,2011,31(3):124-131.
[4]董霞,刘志珍.直流偏磁下单相变压器的传输线模型[J].电机与控制学报,2012,16(10):7-12.
DONG Xia,LIU Zhizhen.Transmission-line model of the singlephase transformer under DC bias[J].Electric Machines and Control,2012,16(10):7-12.
[5]JILES D C,ATHERTON D L.Theory of ferromagnetic hysteresis[J].Journal of Applied Physics,1984,55(6):2115-2120.
[6]李晓萍,彭青顺,李金保,等.变压器铁心磁滞模型参数辨识[J].电网技术,2012,36(2):200-205.
LI Xiaoping,PENG Qingshun,LI Jinbao,et al.Parameter identification of hysteresis loop model for transformer core[J].Power System Technology,2012,36(2):200-205.
[7]JIA Xiao,CHEN Dairong,JIAO Xiulin,et al.Monodispersed Co,Ni-Ferrite nanoparticles with tunable sizes:controlled synthesis,magnetic properties,and surface modification[J].Journal of Chemical Physics C,2008,112(4):911-917.
[8]张甫飞.铁基非晶合金材料的温度特性[C]//中国电子变压器第一届联合学术年会,12月5-7,2003,深圳,中国.2003:47-50.
[9]RAGHUNATHAN A,MELIKHOV Y,SNYDER J E,et al.Theoretical model of temperature dependence of hysteresis based on mean field theory[J].IEEE Transactions on Magnetics,2010,46(6):1507-1510.
[10]ARROTT A,NOAKES J E.Approximate equation of state for nickel near its critical temperature[J].Physical Review Letters,1967,19(14):786-789.
[11]谢光彬,金熙,郎桐,等.基于居里温度的输电线路连接点感温指示器研究[J].电测与仪表,2012,49(556):59-63.
XIE Guangbin,JIN Xi,LANG Tong,et al.The research of contact feeling temperature indicator based on curie temperature for transmission line[J].Electrical Measurement&Instrumentation,2012,49(556):59-63.
[12]MUTHUMUNI D,MCLAREN P G,CHANDRASENA W,et al.Simulation model of an air gapped current transformer[C]//IEEE Power Engineering Society Winter Meeting,January 28-February 1,2001,Columbus,USA.2001:705-709.
[13]何正明,赵妙余,张玲芬,等.铁基非晶合金磁致伸缩的温度效应[J].物理学报,1990,39(4):656-660.
HE Zhengming,ZHAO Miaoyu,ZHANG Lingfen,et al.Effects of temperature on saturation magnetostriction in iron-rich amorphous alloys[J].Acta Physica Sinica,1990,39(4):656-660.
[14]卢志超,鲜于泽,沈保根,等.Fe基非晶和纳米晶合金的热膨胀[J].材料研究学报,1995,9(1):13-15.
LU Zhichao,XIAN Yuze,SHEN Baogen,et al.Thermal expansion properties of Fe-based amorphous and nanocrystalline alloys[J].Chinese Journal of Materials Research,1995,9(1):13-15.
[15]黄军庆,傅明喜,王斌,等.退火温度对非晶合金Fe69Al5Ga2P9.65B4.6Si3C6.75磁性能的影响[J].特种铸造及有色合金,2011,31(12):1142-1144.
HUANG Junqing,FU Mingxi,WANG Bin,et al.Effects of annealingtemperatureonmagneticpropertiesof Fe69Al5Ga2P9.65B4.6Si3C6.75 amorphous alloys[J].Special Casting&Nonferrous Alloys,2011,31(12):1142-1144.

