“科克曼女生问题”的探讨
谌义才
(四川新川航空仪器有限责任公司,四川广汉618300)
1 引 言
“某寄宿学校的15个女生,每天都要三人一行外出散步一次,怎样安排才能使每个学生一周7天内和其他14个女生在三人行中散步各1次.”看似简单的数学题难倒了世界上众多著名数学家,这就是英国数学家科克曼(Thomas Penyngton Kirkma, 1806-1895)于1850年提出的著名的“科克曼女生问题”.
在科克曼发表女生问题的研究之后,西尔维斯特和凯莱对这一问题提出更苛刻的条件.西尔维斯特(15名女生问题:某班级有15名女生,老师每天组织她们出去散步,第三人一行,问如何安排女生顺序使每个女生同其他女生同一行中散步,恰好13周不重复.这一问题直到1974年才由美国的丹尼斯顿借助电子计算机得以确证,v=15如下的13个方案:
星期日 {i,a,b},{8+i,9+i,12+i},{3+i,7+i,10+i},{2+i,6+i,11+i},{1+i,4+i,5+i};
星期一 {2+i,8+i,b},{1+i,6+i,a},{4+i,7+i,11+i},{3+i,5+i,9+i},{i,10+i,12+i};
星期二 {11+i,12+i,b},{4+i,10+i,a},{6+i,7+i,9+i},{1+i,2+i,3+i},{i,5+i,8+i};
星期三 {5+i,7+i,b},{3+i,12+i,a},{2+i,9+i,10+i},{1+i,8+i,11+i},{i,4+i,6+i};
星期四 {4+i,9+i,b},{2+i,5+i,a},{6+i,8+i,10+i},{1+i,7+i,12+i},{i,3+i,11+i};
星期五 {1+i,10+i,b},{9+i,11+i,a},{5+i,6+i,12+i},{3+i,4+i,8+i},{i,2+i,7+i};
星期六 {3+i,6+i,b},{7+i,8+i,a},{5+i,10+i,11+i},{2+i,4+i,12+i},{i,1+i,9+i}.
其中15名女生分别标记为a,b,0,1,2,…,12,而数字i=0,1,…,12.每取i的一个值,所列的5×7个区组就给出了所求的队形安排[1].此后,由“科克曼女生问题”引申出的组合数学中的一般的科克曼三元系存在性问题,一直到1971年才告彻底解决,其中包括中国的优秀数学家陆家羲在内的许多数学家都作出了贡献.从此之后,不但15个女生问题安排问题,哪怕是21个、27个、32个……,甚至是“6N+3”(N为自然数)个的女生散步问题都已解决[2].
“科克曼女生问题”既是一个数学智力题,那就具备一定初等数学知识的人想必都可解,但未必都能解.本文用初等数学知识来解析这道智力题.
2 解析“科克曼女生问题”
用1~15号分别代表15个女生,三人一组按顺序排列组合,则“科克曼女生问题”的15个女生全部排列组合形式见表3.
2.1 选一周的1号女生组合
将2~15号女生任意分成7组,再将1号女生加入,再按顺排组合填入表1.
2.2 选一周的2号女生组合
2号组合亦有7组,在表1中星期一第一组中已有一个2号女生组合(1-2-15),因此在表3中只选定六个2号组合即可.
选星期二第二组的2号组合:在表3中找出2号全部排列组合78个,将有2-15,3-14,4-13,5-12,6-11,7-10,8-9及当天3,14号的全部组合删除,然后任意选一组排列组合(如选2-4-10),并将2-4-10填入表1星期二第二组内.
选星期三第二组的2号组合:在表3中找出2号全部排列组合78个,将有2-15,3-14,4-13,5-12,6-11,7-10,8-9,2-4,2-10,4-10及当天4,13号的全部组合删除,然后任意选一组排列组合(如选2-3-11),并将2-3-11填入表1星期三第二组内.
其余2号组合按此方法进行选择,六个2号组合就全部选定,选定后填入表1内.

表1 科克曼1,2号女生组合散步表
从表1中可以看出,2号女生组合放置的位置与1号女生有所不同.相同点是三人组合都是从小至大排列组合,不同点是:1号女生组合按顺排组合,2号女生组合可任意放置那一天,只要当天不同号即可.至此,1号和2号的组合选择共13组,全部选定.
2.3 其它三人组组合的选择
1号女生组合和2号女生组合共13组选定后,剩下的其它22组三人组合选择难度较大.其选择方法就不能用上述1号女生组合和2号女生组合的选择方法进行选择,必须把剩余组合组列出(限于篇幅,未列出组合组).对组合组进行筛选,确定22组的组合位置.在此给出科克曼女生散步一组解,见表2.
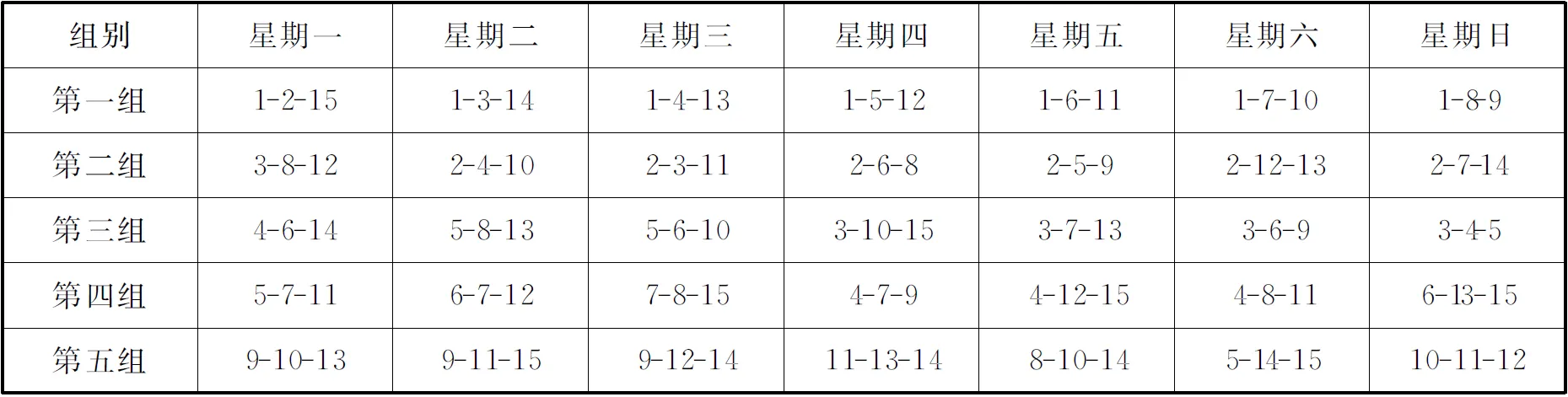
表2 科克曼15女生散步一组解
从表2组合中可以看出几个特点:
第一、每天15个女生分成五组,三人组合全部按顺排组合.
第二、第一组1号女生组合中间女生在排列位置上全部采用顺排(从小到大)的方法,主要是考虑到后面计算组解的准确数.
第三、第二组的2号女生组合位置,可任意放置,只要当天不出现同号即可.
第四,同一天第一组至第五组前面女生全部从小到大排列.
3 “科克曼女生问题”组合位置发生变化时,对组解的影响
若将表1中的1号组合中9号与10号对调,2号组合不变,“科克曼女生问题”的组解就会发生变化,在此给出科克曼女生散步一组解,见表4.
若将表中的2号组合中13号与14号对调,1号组合不变,“科克曼女生问题”的组解亦会发生变化,在此给出科克曼女生散步一组解,见表5.
合理选择排水管材对于管道的使用寿命、日常维护以及控制工程造价都起到非常关键的作用,本次施工选用高密度聚乙烯(HDPE)双壁波纹管、排水检查井选用塑料检查井(成品),此类管道、井体不仅抗压耐冲击、内壁光滑摩阻小,而且重量轻、施工快捷[2]。
由表4和表5组解可见,无论是1号组合位置还是2号组合位置发生变化,“科克曼女生问题”的组解结果都会发生变化.由此可见,在满足题意的前提下,可以对1号组合或2号组合进行调整,也可以同时对1号组合和2号组合进行调整.通过对三人组合的调整,可以解得“科克曼女生问题”的不同组解.
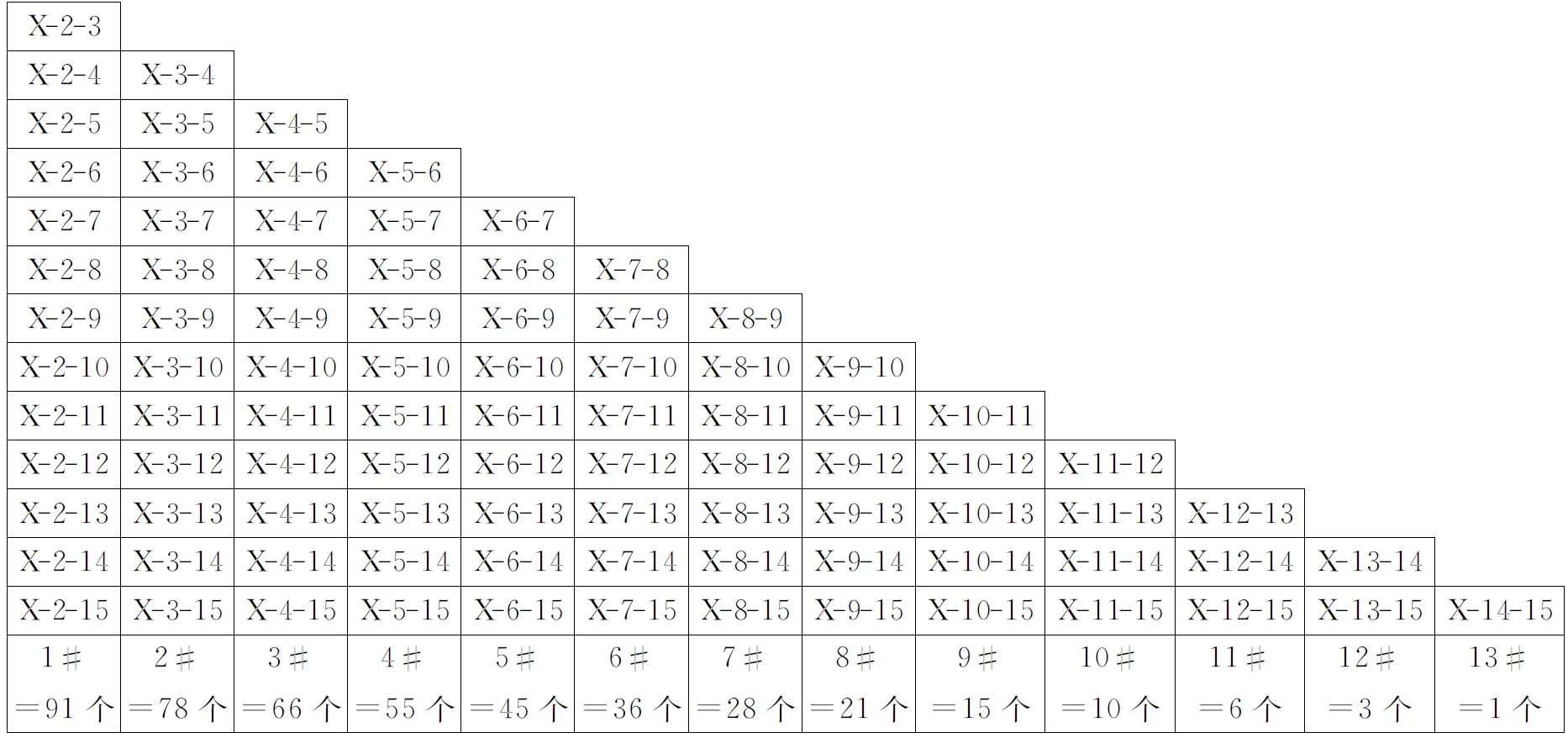
表3 “科克曼女生问题”三人组合全部排列组合图(从小至大排列,共455个)
注X为女生代号.用X=1代入,可得1号女生共91组排列组合;用X=2代入并删除左1列,可得2号女生共78组排列组合;用X=3代入,并删除左2列,可得3号女生共66组排列组合;其余号依此类推,最后一个就是13号女生的排列组合,只有1个为13-14-15.

表4 科克曼15女生散步一组解
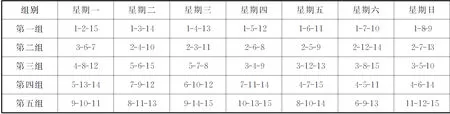
表5 科克曼15女生散步一组解
4 “科克曼女生s问题”存在十三系列解
在研究“科克曼女生问题”时,发现 “科克曼女生问题” 存在“十三系列解”.
1号女生存在一个“十三系列解” ,见表6.从表6中可以看出,表内列出了1号女生的全部排列组合,并且在每个系列中,1号女生与其余号女生均见面一次.
2号女生存在三个“十三系列解” ,见表7、表8、表9.从表7、表8、表9中可以看出,各表内列出了2号女生的全部排列组合,并且在每个系列中,2号女生与其余号女生均见面一次.
1,2号女生十三系列解可以合并,同一天出现同号时调整2号组合星期位置.
其余号女生(X)可以用1号女生十三系列解生成X号女生十三系列解,具体操作方法是:将X号与1号对换即可,再调整为顺排形式.
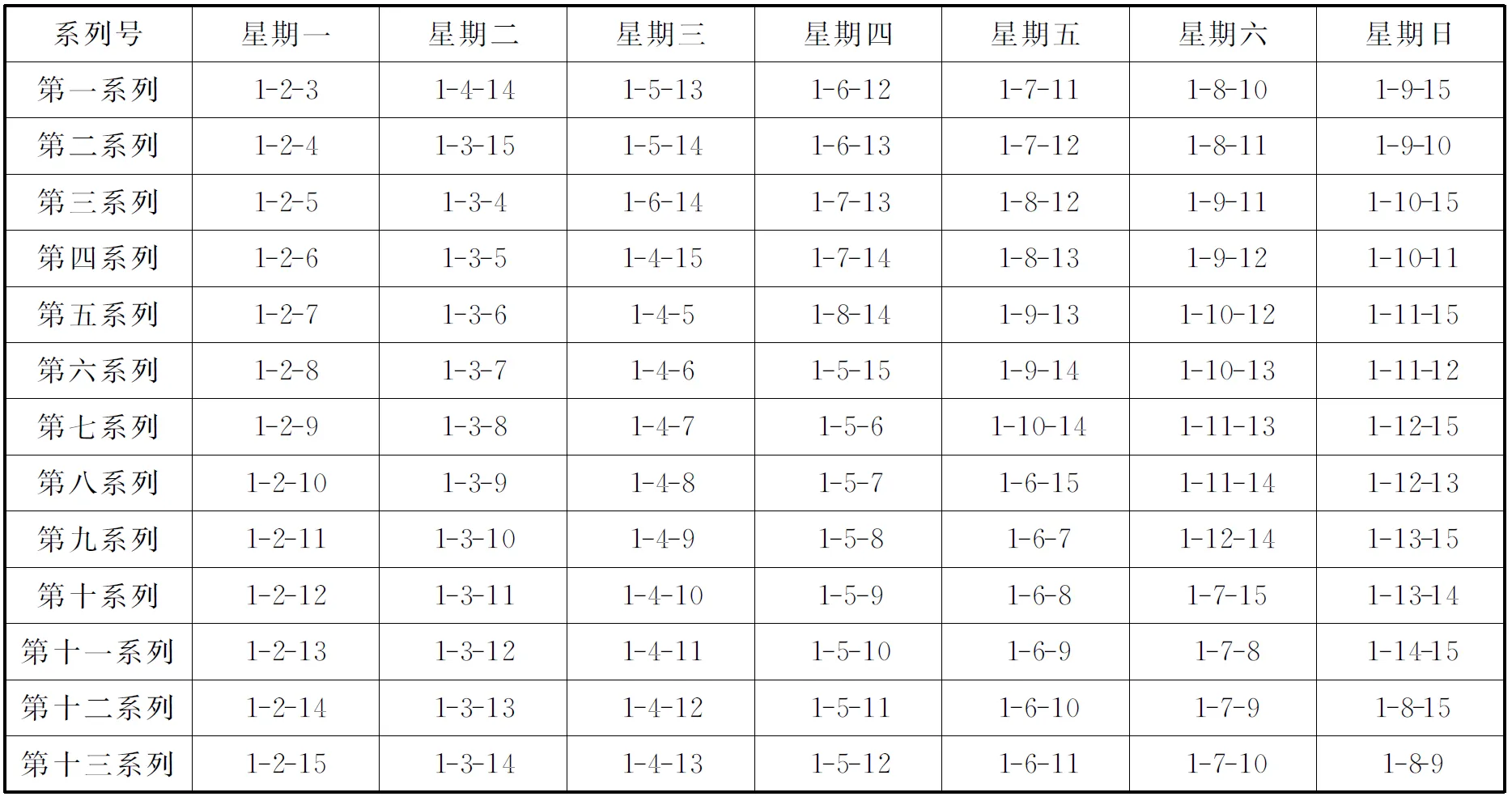
表6 “科克曼女生问题” 1号女生十三系列解
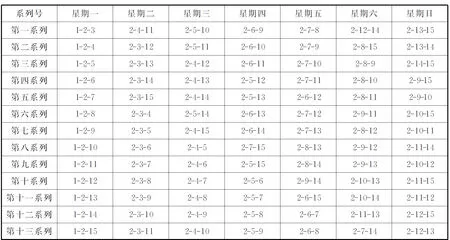
表7 “科克曼女生问题” 2号女生十三系列解之一
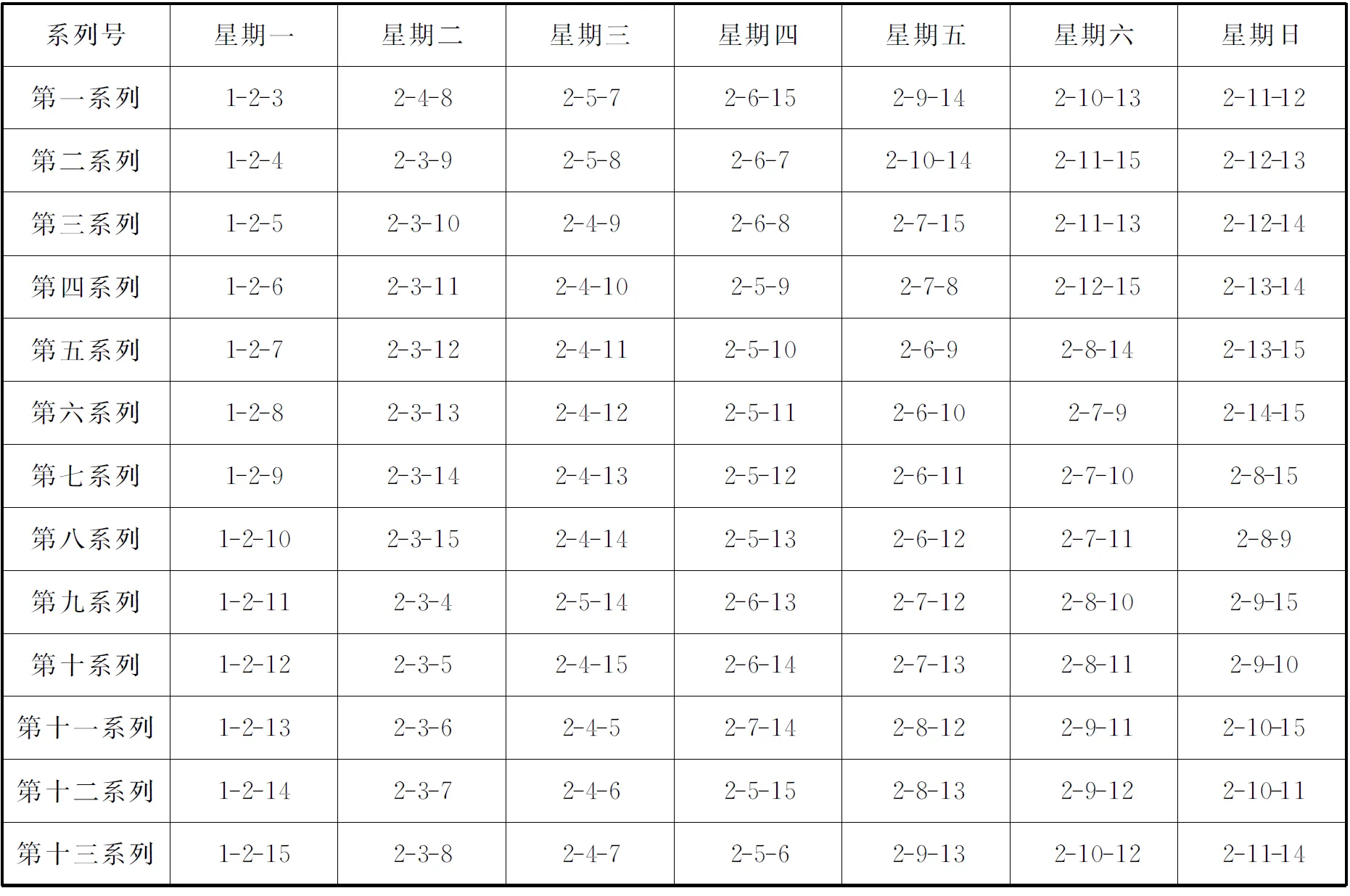
表8“科克曼女生问题” 2号女生十三系列解之二
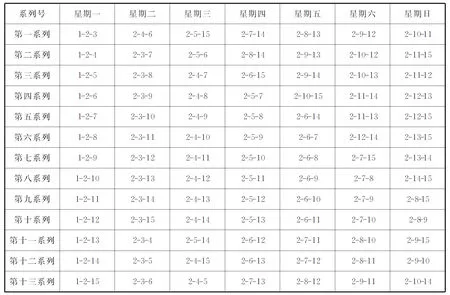
表9 “科克曼女生问题” 2号女生十三系列解之三
5 “科克曼女生问题”引申出的“6N+3”(N为自然数)个的女生散步问题的研究
“科克曼女生问题”存在十三系列解,由此推论出“6N+3” (N为自然数)个的女生散步问题都存在“6N+1”系列解”.
6 “科克曼女生问题”组解的计算
若只考虑一周第一组的组合变化,“科克曼女生问题”的组解有13×11×9×7×5×3×1=135135组.
若只考虑星期一一天的组合变化,“科克曼女生问题”的组解有91×55×28×10×1=1401400组.
若只考虑一周第一组及星期一第二至第五组的组合变化,“科克曼女生问题”的组解有670269600组,见表10.星期二至星期日的第二组至第五组的组合变化数计算起来很复杂,但其变化数只有数百种(约608种)的变化.由此可见,“科克曼女生问题”的组解约有670269600×608=407523916800组.
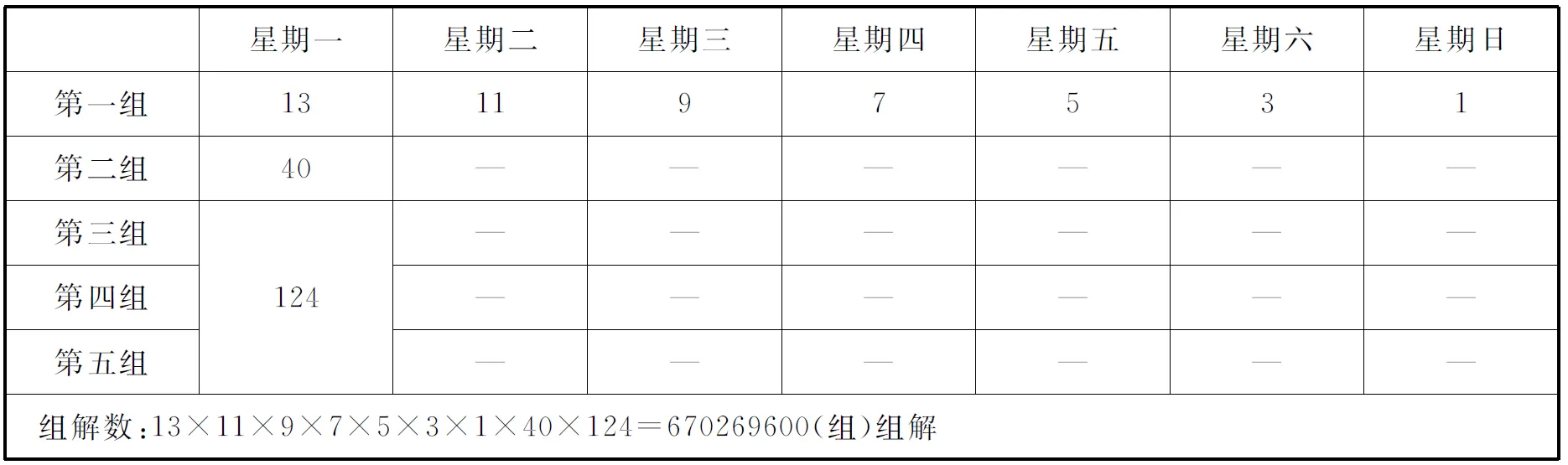
表10 “科克曼女生问题”组解计算
7 “科克曼女生问题”组解的应用
“科克曼女生问题”的组解在医药试验设计上得到广泛运用.在满足“科克曼女生问题”题意的前提下,可以对两个号任意组合,随意而动.就象练气功一样,意到那里气就到那里.兹举“科克曼女生问题”一组解(见表11).从表11中看1号组合和2号组合,其组合方式就象2条巨龙在那里舞动.
“科克曼女生问题” 一组解(表2组解:第十三系列)可以通过1号女生 “十三系列解” ,变换出一个“科克曼女生问题”十三系列组解,见表12.
8 结 论
本文给出了“科克曼女生问题”的解答方法:
第一步,选一周第一组的1号组合7个.
第二步,再选一周第二组的2号组合6个.
第三步,列出其余22组全部组合进行筛选,确定22组组合位置.
注 亦可以任意选择2个号进行组合(7+6)个,再确定其余22组组合位置.
“科克曼女生问题”存在十三系列解:
“科克曼女生问题”1号女生存在一个1号女生十三系列解.“科克曼女生问题”2号女生存在三个2号女生十三系列解,并且1、2号女生十三系列解可以合并.
“科克曼女生问题”一组解可以通过1号或2号女生十三系列解变换出十三系列组解.
“科克曼女生问题”引申出的“6N+3”(N为自然数)个的女生散步问题,都存在“6N+3”系列解.
“科克曼女生问题”是组合设计问题.“科克曼女生问题”解题三步曲和十三解系列图应用在医药试验设计上,医药试验设计将迎来一场新的技术革命.
科克曼女生问题的组解:
科克曼女生问题的组解若只考虑一周第一组的组合变化和第一天第二组至第五组的组合变化,则科克曼女生问题的组解有670269600组.若考虑全部组合变化,“科克曼女生问题”的组解约有407523916800组.
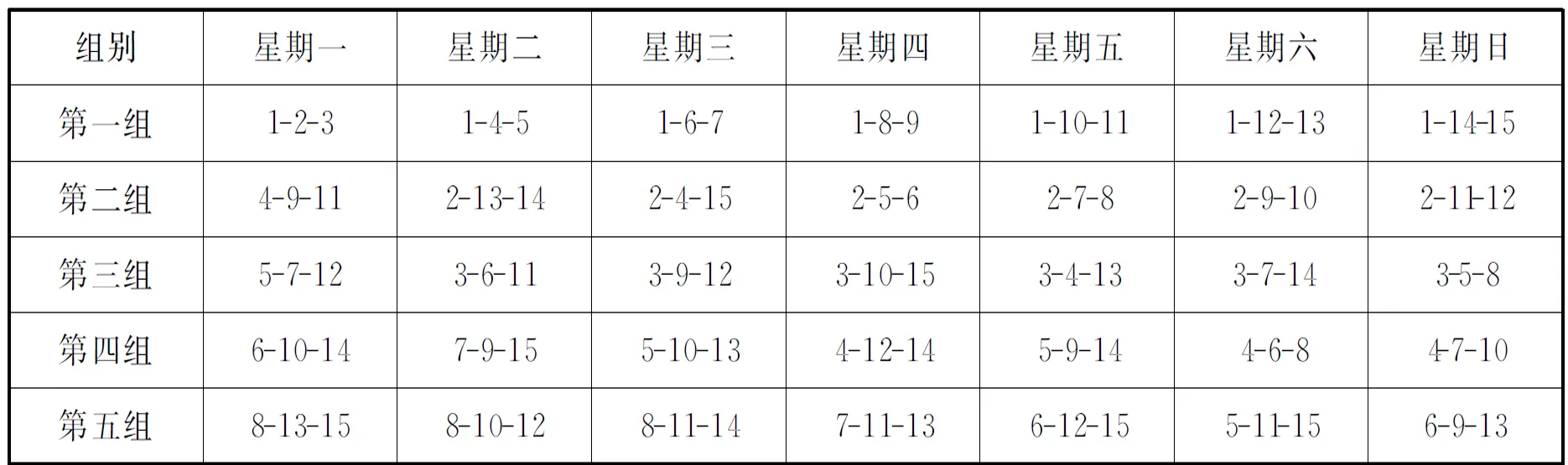
表11 科克曼15女生散步一组解
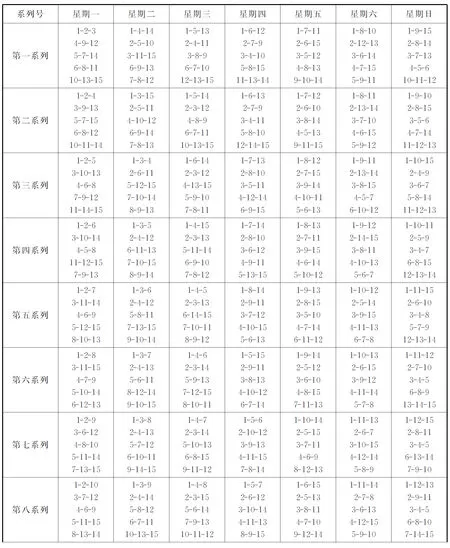
表12 “科克曼女生问题”十三系列组解

表12(续)
[参 考 文 献]
[1] 杨雅琴,李秋月,马腾宇.组合数学[M].北京:国防工业出版社,2013:154-156.
[2] 范晓英.“科克曼女生问题”早已解决[N].江南时报,2002-05-19(10).

